Изобретение относится к области адаптивных систем и может быть использовано для адаптивной фильтрации стохастических сигналов и параметров состояния стохастических систем.
Известен способ фильтрации стохастических сигналов и параметров состояния стохастических систем, обеспечивающий оптимальную по среднеквадратическому критерию оценку измеряемого сигнала или вектора состояния, - калмановская фильтрация [Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 2004. - 304с.; Синицын И.Н. Фильтры Калмана и Пугачева. - М.: Логос, 2006. - 640с.]. Недостатком данного способа является необходимость точного априорного задания вероятностных характеристик возмущений, действующих на объект, т.к. для реальных информационно-измерительных систем, функционирующих в условиях различных помех, параметры возмущений объекта или меняются случайным образом во времени, или известны приближенно [A. Ferrero, R. Ferrero, W. Jiang, S. Salicone. The Kalman Filter Uncertainty Concept in the Possibility Domain, IEEE Trans. Instrum. Meas. 68 (2019), р.р.4335–4347].
Известны способы, использующие для обеспечения устойчивости калмановской фильтрации при условии априорной неопределенности интенсивности возмущений введение эмпирических масштабных коэффициентов при вычислении апостериорной ковариационной матрицы или дисперсионной матрицы возмущений [E.P. Herrera, H. Kaufmann. Adaptive methods of Kalman filtering for personal positioning systems, in: 23rd Int. Tech. Meet. Satell. Div. Inst. Navig. 2010, ION GNSS 2010; Патент № 1639377. Модифицированный нелинейный фильтр Калмана, СССР, Н03Н 21/00; Патент № 1651355. Регуляризованный фильтр Калмана, СССР, Н03Н 21/00; Патент № 1800588. Адаптивный фильтр Калмана, СССР, Н03Н 21/00; Патент № 2160496. Модифицированный фильтр Калмана, РФ, Н03Н 21/00]. Недостатком этих способов является отсутствие строгих критериев выбора масштабных коэффициентов и процедуры их вычисления, а также обоснования повышения точности фильтрации, что не позволяет обеспечить требуемую точность и устойчивость процесса фильтрации в общем случае. Известен способ, использующий для обеспечения устойчивости калмановской фильтрации расширение размерности вектора состояния [D. Wang, H. Ly, J. Wu. Augmented Cubature Kalman filter for nonlinear RTK/MIMU integrated navigation with non-additive noise, Measurement. 97, 2017, р.р.111–125]. Недостатком данного способа являются существенные вычислительные затраты на его реализацию.
Известен также способ, обеспечивающий оценку дисперсионной матрицы помех измерения из условия минимума ковариации обновляющей последовательности [R. Mehra. On the identification of variances and adaptive Kalman filtering, IEEE Trans. Automat. Contr. 15, 1970, рр.175-184]. Недостатком данного способа является невозможность адаптивного оценивания в реальном времени в силу необходимости предварительного вычисления ковариации обновляющей последовательности и низкая точность фильтрации при отсутствии возможности выбора больших временных интервалов при вычислении ковариации обновляющей последовательности.
Наиболее близким к предлагаемому способу является способ, обеспечивающий оценку дисперсионной матрицы помех измерения [Патент № 2755499. Способ адаптивной фильтрации, РФ, Н03Н 21/00, G06E 3/00] за счет адаптивного определения дисперсионной матрицы помех измерения на основе точных измерений, поступающих в нерегулярные (или случайные) моменты времени.
Недостатком данного способа является невозможность адаптивного определения коэффициента усиления фильтра в целом.
Заявленный способ направлен на решение задачи обеспечения устойчивости и повышения точности калмановской фильтрации за счет адаптивного определения коэффициента усиления фильтра в процессе текущего оценивания стохастических сигналов и параметров состояния стохастических систем на основе точных измерений, поступающих в нерегулярные (или случайные) моменты времени.
Поставленная задача возникает в комплексированных адаптивных управляющих и информационно-измерительных системах, функционирующих в условиях неопределенных возмущений, в которых осуществляется коррекция первичных зашумленных ("грубых") измерений по измерениям, выступающим в качестве эталонных (через интервалы времени, превышающие такт первичных измерений и не всегда регулярные (зачастую случайные)). Например, в инерциально-спутниковых навигационных системах (НС), где осуществляется коррекция измерений инерциальной НС, погрешности которых растут со временем, по измерениям спутниковой НС, которые выступают в качестве эталонных [Резниченко В.И., Малеев П.И., Смирнов М.Ю. Спутниковая коррекция параметров ориентации морских объектов // Навигация и гидрография, Том 27, 2008. – С. 25-32]; в НС роботов, в которых коррекция навигационных параметров робота осуществляется с учетом нулевой скорости его ступни (или нижней точки колеса) в момент касания поверхности земли [Луни М. Оптимизация навигационных характеристик мобильного робота // Компоненты и технологии, № 1, 2012. – С. 48-50], в информационно-измерительных системах различных транспортных систем (морских, железнодорожных и т.д.), где коррекция параметров ориентации и навигации осуществляется в момент прохождения ими реперных точек (буев, светофоров, радиочастотных меток и др.) с точно известными координатами [Цыплаков А.А. Введение в моделирование в пространстве состояний // Квантиль, № 9, 2011. – С. 1-24] и др.
Сущность способа состоит в том, что при наличии текущих дискретных зашумленных измерений осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта, а в момент поступления точных измерений формируется разность между вектором точных измерений и произведением переходной матрицы состояния системы на вектор оценки в предыдущий момент времени, именуемая далее как текущая вариация оценки, определяется разность между вектором калмановской невязки и произведением матрицы измерений на текущую вариацию оценки, именуемая далее как псевдоневязка, отличающийся тем, что при этом одновременно формируется произведение переходной матрицы состояния системы, ковариационной матрицы, транспонированной переходной матрицы состояния системы, транспонированной матрицы измерений и обратной дисперсионной матрицы помех измерения, именуемое далее как вспомогательная матрица, после чего формируются векторы произведения вспомогательной матрицы на псевдоневязку и произведения дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку, после формирования которых вектор элементов матрицы коэффициентов адаптации фильтра по точным измерениям формируется как произведение диагональной матрицы, элементы которой обратны соответствующим значениям элементов вектора произведения вспомогательной матрицы на псевдоневязку, на вектор разности между текущей вариацией оценки и произведением дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку, а далее осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта по текущим дискретным зашумленным измерениям со вновь сформированной матрицей коэффициентов адаптации фильтра до момента поступления следующих точных измерений, после которого процедура адаптивной фильтрации повторяется аналогично вышеизложенному.
В основу способа положены следующие теоретические результаты.
Оценка вектора состояния объекта 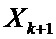 в (k+1)-й момент времени дискретным фильтром Калмана [Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 2004. - 304с.] имеет вид:
в (k+1)-й момент времени дискретным фильтром Калмана [Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. - М.: Радио и связь, 2004. - 304с.] имеет вид:
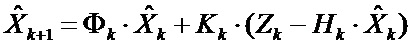 , (1)
, (1)
где 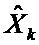 - оценка вектора состояния объекта в k-й момент времени;
- оценка вектора состояния объекта в k-й момент времени;
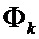 - переходная матрица состояния объекта;
- переходная матрица состояния объекта;
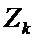 - вектор измерений:
- вектор измерений:
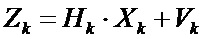 ,
,
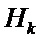 - матрица измерений, отображающая пространство векторов состояния объекта в пространство векторов измерений;
- матрица измерений, отображающая пространство векторов состояния объекта в пространство векторов измерений;
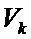 - центрированная гауссовская последовательность с дисперсионной матрицей
- центрированная гауссовская последовательность с дисперсионной матрицей 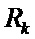 ,
,
 - коэффициент усиления фильтра:
- коэффициент усиления фильтра:
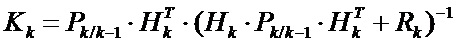 , (2)
, (2)
 ,
,
 ,
,
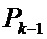 - ковариационная матрица;
- ковариационная матрица;
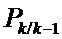 - экстраполированная ковариационная матрица;
- экстраполированная ковариационная матрица;
Е - единичная матрица,
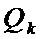 - дисперсионная матрица возмущения, действующего на объект.
- дисперсионная матрица возмущения, действующего на объект.
Для обеспечения возможности адаптации коэффициента усиления фильтра к изменениям условий функционирования системы, ее параметров и пр. неопределенным возмущениям, экстраполированную ковариационную матрицу, определяющую коэффициент усиления, сформируем следующим образом:
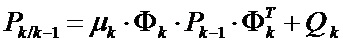 , (3)
, (3)
где µk - диагональная матрица коэффициентов адаптации фильтра.
Исходя из представленной формы коэффициента усиления фильтра, задачу его адаптации по точным измерениям сформулируем как задачу нахождения матрицы µk из условия совпадения в соответствующий момент времени вектора оценок 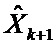 (1) с точным вектором состояния системы
(1) с точным вектором состояния системы 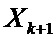 (точными измерениями).
(точными измерениями).
Далее используем полное выражение Калмановского коэффициента усиления, полученное подстановкой (3) в (2):
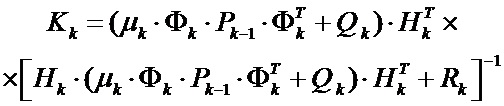 ,
,
где для удобства последующего решения введем обозначение 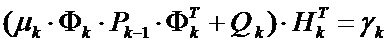 и запишем выражение коэффициента Kk следующим образом:
и запишем выражение коэффициента Kk следующим образом:
 . (4)
. (4)
В этом случае уравнение оценки (1) примет вид:
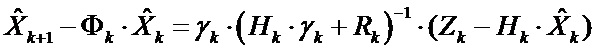 (5)
(5)
и относительно матрицы 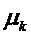 , входящей в матрицу
, входящей в матрицу 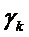 , представляет собой нелинейное векторное уравнение, решение которого традиционными численными методами требует многократного применения весьма затратной процедуры обращения матрицы. Для возможности его аналитического решения проведем следующие построения.
, представляет собой нелинейное векторное уравнение, решение которого традиционными численными методами требует многократного применения весьма затратной процедуры обращения матрицы. Для возможности его аналитического решения проведем следующие построения.
Т.к. при использовании точных наблюдений  , то, вводя обозначения
, то, вводя обозначения 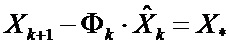 ,
,  , представим уравнение (5) как:
, представим уравнение (5) как:
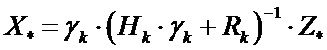 . (6)
. (6)
Умножая обе части уравнения (6) на обратную матрицу 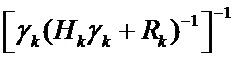 , имеем:
, имеем:
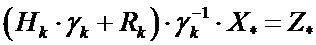 ,
,
или
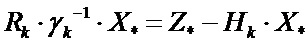 . (7)
. (7)
Умножив далее обе части уравнения (7) на матрицу  , приведем его к виду, линейному относительно
, приведем его к виду, линейному относительно 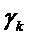 , а, следовательно, и относительно
, а, следовательно, и относительно 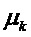 :
:
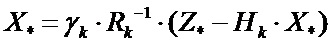 . (8)
. (8)
Для окончательного решения данного уравнения относительно  раскроем выражение
раскроем выражение 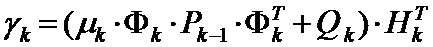 и получим:
и получим:
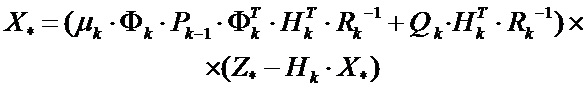 (9)
(9)
Вводя для упрощения последующего вывода обозначения 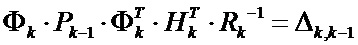 и
и 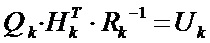 , представим уравнение (9) в виде:
, представим уравнение (9) в виде:
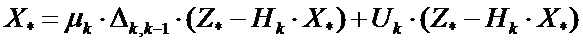 . (10)
. (10)
Обозначая векторы 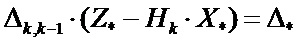 ,
, 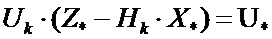 , приведем уравнение (10) к следующей форме:
, приведем уравнение (10) к следующей форме:
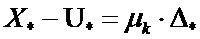 . (11)
. (11)
Уравнение (11) легко допускает аналитическое решение относительно всех элементов диагональной матрицы µk, если учесть возможность представления произведения 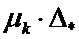 в виде
в виде 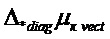 , где
, где
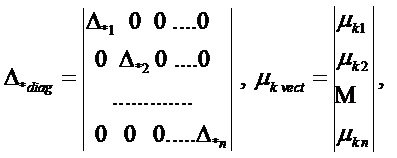
 элементы, соответственно, вектора
элементы, соответственно, вектора 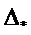 и матрицы µk.
и матрицы µk.
В этом случае имеем искомое выражение вектора элементов матричного коэффициента адаптации в виде:
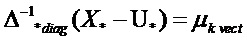 ,
,
где 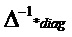 - обратная матрица, легко вычисляемая аналитически в силу ее диагональности:
- обратная матрица, легко вычисляемая аналитически в силу ее диагональности:
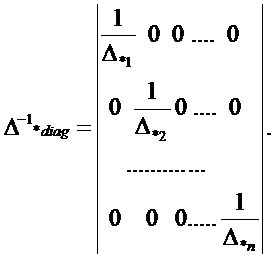
Далее осуществляется калмановская фильтрация наблюдаемого вектора состояния объекта по текущим дискретным зашумленным измерениям с полученным значением матричного коэффициента адаптации µk, неизменным до момента поступления следующих точных измерений, после которого процедура адаптивной фильтрации повторяется аналогично описанному выше. Исходя из изложенного, заявляемый способ адаптивной фильтрации на основе формирования коэффициента усиления фильтра по точным наблюдениям реализуется следующим образом:
- по текущим дискретным зашумленным измерениям осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта;
- в момент поступления точных измерений формируется разность (Х*) между вектором точных измерений ( ) и произведением переходной матрицы состояния системы (
) и произведением переходной матрицы состояния системы ( ) на вектор оценки в предыдущий момент времени (
) на вектор оценки в предыдущий момент времени (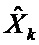 ), именуемая далее как текущая вариация оценки;
), именуемая далее как текущая вариация оценки;
- определяется разность между вектором калмановской невязки (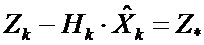 ) и произведением матрицы измерений (
) и произведением матрицы измерений (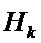 ) на текущую вариацию оценки (Х*), именуемая далее как псевдоневязка;
) на текущую вариацию оценки (Х*), именуемая далее как псевдоневязка;
- формируется произведение следующих матриц: переходной матрицы состояния системы (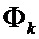 ), ковариационной матрицы (
), ковариационной матрицы ( ), транспонированной переходной матрицы состояния системы (
), транспонированной переходной матрицы состояния системы ( ), транспонированной матрицы измерений (
), транспонированной матрицы измерений (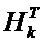 ) и обратной дисперсионной матрицы помех измерения (
) и обратной дисперсионной матрицы помех измерения (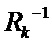 ), именуемое далее как вспомогательная матрица (
), именуемое далее как вспомогательная матрица (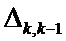 );
);
- после чего формируются векторы: произведение (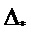 ) вспомогательной матрицы на псевдоневязку и произведение (
) вспомогательной матрицы на псевдоневязку и произведение (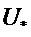 ) дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку;
) дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку;
- вектор элементов матрицы коэффициентов адаптации фильтра по точным измерениям формируется как произведение диагональной матрицы, элементы которой определяются как величины, обратные соответствующим значениям элементов вектора (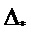 ) произведения вспомогательной матрицы на псевдоневязку, на вектор разности между текущей вариацией оценки (Х*) и произведением (
) произведения вспомогательной матрицы на псевдоневязку, на вектор разности между текущей вариацией оценки (Х*) и произведением (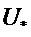 ) дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку;
) дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку;
- далее осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта по текущим дискретным зашумленным измерениям со вновь сформированной матрицей коэффициентов адаптации фильтра до момента поступления следующих точных измерений, после которого процедура адаптивной фильтрации повторяется аналогично вышеизложенному.
В результате адаптации процесса фильтрации к неопределенным возмущениям обеспечивается повышение точности и устойчивости оценки вектора состояния наблюдаемой стохастической системы.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ адаптивной фильтрации | 2022 |
|
RU2782955C1 |
| Способ адаптивной фильтрации | 2021 |
|
RU2755499C1 |
| Робастный дискретный стохастический фильтр | 2023 |
|
RU2804256C1 |
| РОБАСТНЫЙ ДИСКРЕТНЫЙ СТОХАСТИЧЕСКИЙ ФИЛЬТР | 2024 |
|
RU2830681C1 |
| РОБАСТНЫЙ СТОХАСТИЧЕСКИЙ ФИЛЬТР | 2024 |
|
RU2826922C1 |
| Робастный стохастический фильтр | 2021 |
|
RU2755677C1 |
| СПОСОБ ОПЕРАТИВНО-ТЕХНИЧЕСКОЙ ОХРАНЫ РУБЕЖЕЙ ОБЪЕКТОВ И ГРАНИЦ | 2018 |
|
RU2705770C1 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
Изобретение относится к области адаптивных систем. Технический результат - обеспечение устойчивости и повышение точности калмановской фильтрации. Для этого предложен способ адаптивной фильтрации, в котором осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта при наличии текущих дискретных зашумленных измерений. Причем осуществляется адаптивное определение коэффициента усиления фильтра в процессе текущего оценивания стохастических сигналов и параметров состояния стохастических систем на основе точных измерений, поступающих в нерегулярные (или случайные) моменты времени путем использования переходной матрицы состояния системы, матрицы измерений, ковариационной матрицы, транспонированной переходной матрицы состояния системы, транспонированной матрицы измерений и обратной дисперсионной матрицы помех измерения, после чего осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта по текущим дискретным зашумленным измерениям со вновь сформированной матрицей коэффициентов адаптации фильтра до момента поступления следующих точных измерений, после которого процедура повторяется.
Способ адаптивной фильтрации, состоящий в том, что при наличии текущих дискретных зашумленных измерений осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта, а в момент поступления точных измерений формируется разность между вектором точных измерений и произведением переходной матрицы состояния системы на вектор оценки в предыдущий момент времени, именуемая далее как текущая вариация оценки, определяется разность между вектором калмановской невязки и произведением матрицы измерений на текущую вариацию оценки, именуемая далее как псевдоневязка, отличающийся тем, что при этом одновременно формируется произведение переходной матрицы состояния системы, ковариационной матрицы, транспонированной переходной матрицы состояния системы, транспонированной матрицы измерений и обратной дисперсионной матрицы помех измерения, именуемое далее как вспомогательная матрица, после чего формируются векторы произведения вспомогательной матрицы на псевдоневязку и произведения дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку, после формирования которых вектор элементов матрицы коэффициентов адаптации фильтра по точным измерениям формируется как произведение диагональной матрицы, элементы которой обратны соответствующим значениям элементов вектора произведения вспомогательной матрицы на псевдоневязку, на вектор разности между текущей вариацией оценки и произведением дисперсионной матрицы возмущения объекта на транспонированную матрицу измерений, на обратную дисперсионную матрицу помех измерения и псевдоневязку, а далее осуществляется калмановская фильтрация вектора состояния наблюдаемого объекта по текущим дискретным зашумленным измерениям со вновь сформированной матрицей коэффициентов адаптации фильтра до момента поступления следующих точных измерений, после которого процедура адаптивной фильтрации повторяется аналогично вышеизложенному.
| Способ адаптивной фильтрации | 2021 |
|
RU2755499C1 |
| СПОСОБ МНОГОСТУПЕНЧАТОЙ ФИЛЬТРАЦИИ ДЛЯ СИСТЕМ АВТОСОПРОВОЖДЕНИЯ | 2015 |
|
RU2616188C1 |
| Робастный стохастический фильтр | 2021 |
|
RU2755677C1 |
| US 5051751 A1, 24.09.1991. | |||
Авторы
Даты
2022-11-08—Публикация
2022-03-16—Подача