Изобретение относится к бортовым авиационным навигационным системам, применимым на пилотируемых и беспилотных воздушных судах.
Уровень техники
В соответствии с требованиями Международной организации гражданской авиации (ИКАО) процессе во время полета требуется выдерживать заданные значения целостности измерений авиационных приемоизмерителей ГНСС. При этом под целостностью понимается способность системы согласно вероятностным и точностным требованиям, предъявляемым к каждому этапу полета, обнаруживать отказ в показаниях бортовых приемоизмерителей ГНСС, а также обеспечивать своевременное формирование и выдачу сигнализации потребителю информации.
В основу алгоритмов контроля положено допущение о том, что в каждый момент времени может иметь место отказ только одного спутника, которое было сделано на основе статической оценки данных, полученных в результате научно-практических исследований, проведенных военно-воздушными силами США. Для вычисления местоположения потребителя в трехмерном пространстве и смещения генератора времени приемоизмерителя относительно времени используемой спутниковой навигационной системы необходимы показания как минимум четырех НКА, имеющих соответвующий геометрический фактор. Для обнаружения единственного аномального измерения псевдодальности до НКА отказа в показаниях ГНСС необходимо наблюдение дополнительного (пятого) НКА. Для решения задачи исключения отказа необходимо принимать сигналы от шести НКА.
В открытых источниках приводятся описания различных схем построения автономных алгоритмов контроля целостности, основанных на общем принципе, заключающемся в непрерывной вероятностной проверке измерений, выполняемых спутниковым навигационным оборудованием потребителей. Обнаружение отказа базируется на вероятностной проверке и принятии одной из двух конкурирующих гипотез: гипотезы о нормальной работе системы 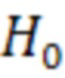 (нулевой гипотезы) или гипотезы об отказе
(нулевой гипотезы) или гипотезы об отказе 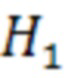 (альтернативной гипотезы).
(альтернативной гипотезы).
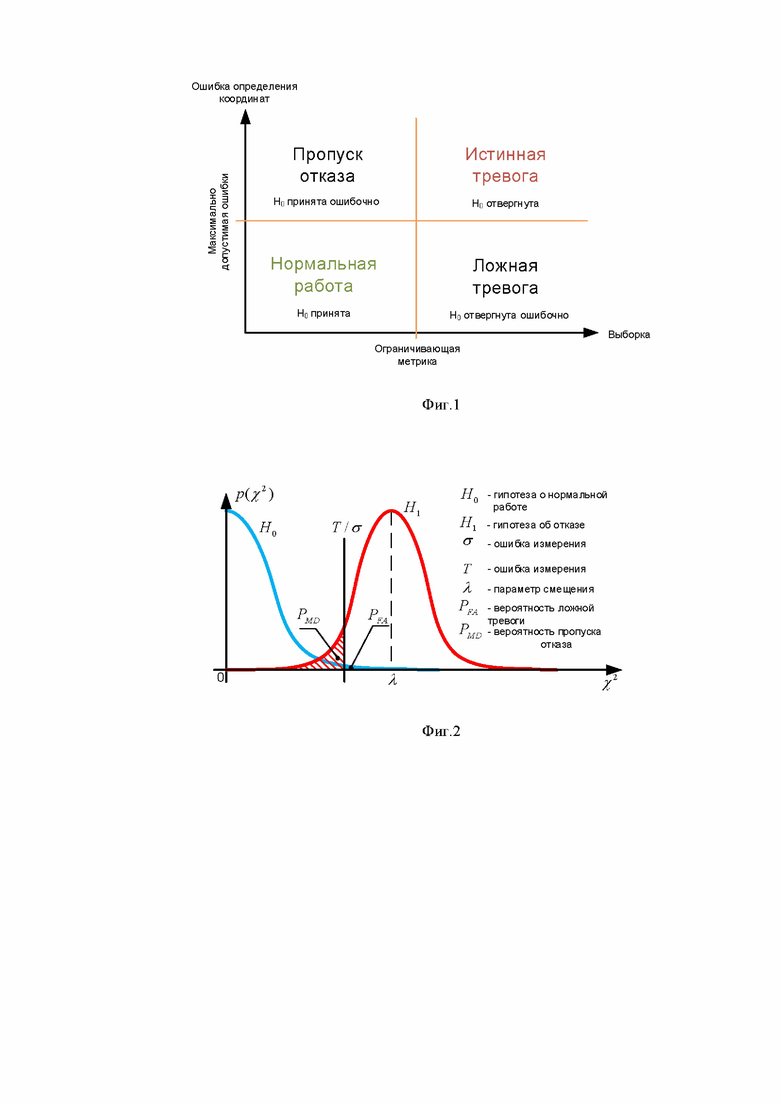
Вероятностные методы, применяемые в различных алгоритмах контроля целостности показаний ГНСС, основаны на ряде случайных переборов, необходимых для принятия или отвержения нулевой гипотезы (согласно диаграмме, приведенной на фиг.1). Процесс проверки гипотезы сводится к сравнению искомой переменной 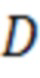 с ограничивающей метрикой
с ограничивающей метрикой 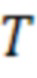 (далее просто границей).
(далее просто границей).
Обнаружение отказа выполняется по критерию (1):
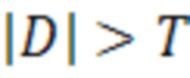 .
(1)
.
(1)
Если величина искомой переменной 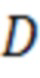 меньше ограничивающей метрики
меньше ограничивающей метрики 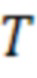 , то принимается гипотеза о нормальной работе
, то принимается гипотеза о нормальной работе 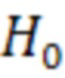 , в противном случае - гипотеза об отказе
, в противном случае - гипотеза об отказе 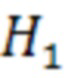 .
.
Возможны четыре исхода работы алгоритма контроля (фиг.1): Нормальная работа, Истинная тревога, Пропуск отказа (2) и Ложная тревога (3). Вероятности последних двух событий могут быть записаны как:
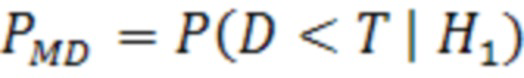 , (2)
, (2)
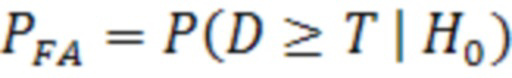 . (3)
. (3)
В приведенных соотношениях граница 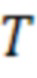 является функцией параметров максимально допустимой ошибки определения координат ВС в плане (Horizontal alarm limit - HAL), вероятности ложной тревоги PFA и пропуска отказа PMD (фиг.2). В случае превышения искомой переменной
является функцией параметров максимально допустимой ошибки определения координат ВС в плане (Horizontal alarm limit - HAL), вероятности ложной тревоги PFA и пропуска отказа PMD (фиг.2). В случае превышения искомой переменной 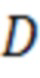 границы
границы 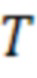 во время нормальной работы системы (при отсутствии отказа) генерируется ложная тревога. Вероятность ложной тревоги представляет собой площадь под кривой, отсекаемой границей
во время нормальной работы системы (при отсутствии отказа) генерируется ложная тревога. Вероятность ложной тревоги представляет собой площадь под кривой, отсекаемой границей 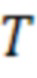 справа от несмещенной плотности вероятности. Кривая смещенной плотности вероятности соответствует отказу в показаниях приемо-измерителя, приводящему к превышению максимально допустимой ошибки в плане HAL для данного этапа полета. Вероятность пропуска отказа имеет геометрический смысл, аналогичный смыслу вероятности ложной тревоги, представляя собой площадь, отсекаемую границей
справа от несмещенной плотности вероятности. Кривая смещенной плотности вероятности соответствует отказу в показаниях приемо-измерителя, приводящему к превышению максимально допустимой ошибки в плане HAL для данного этапа полета. Вероятность пропуска отказа имеет геометрический смысл, аналогичный смыслу вероятности ложной тревоги, представляя собой площадь, отсекаемую границей 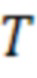 слева от кривой смещенной плотности вероятности.
слева от кривой смещенной плотности вероятности.
При решении задачи автономного контроля целостности показаний ГНСС в аппаратуре потребителя используется линейная модель, применяемая при решении навигационной задачи. Измерения (4) записываются как линейные функции поправок к грубым координатам текущего местоположения:
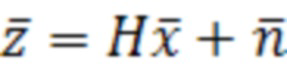 , (4)
, (4)
где 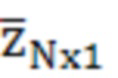 - вектор линеаризованных измерений (скомпенсированных предварительной информацией невязок измерений);
- вектор линеаризованных измерений (скомпенсированных предварительной информацией невязок измерений);
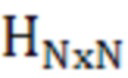 - матрица наблюдения;
- матрица наблюдения;
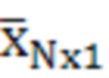 - вектор состояния (содержит три поправки к координатам пользователя X, Y, Z в геоцентрической системе координат и смещение времени
- вектор состояния (содержит три поправки к координатам пользователя X, Y, Z в геоцентрической системе координат и смещение времени 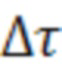 );
);
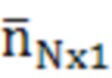 - вектор нормально распределенных ошибок измерений псевдодальностей;
- вектор нормально распределенных ошибок измерений псевдодальностей;
N - размерность вектора измерений.
С помощью МНК производится оценка вектора измерений (5):
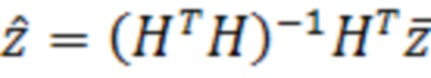 , или
, или 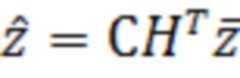 , (5)
, (5)
где 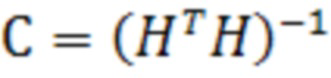 - матрица ковариации.
- матрица ковариации.
Разница между линеаризованными измерениями и их оценкой называется невязкой псевдодальностей (6):
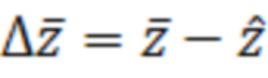 . (6)
. (6)
Невязка может быть вычислена с помощью выражения (7):
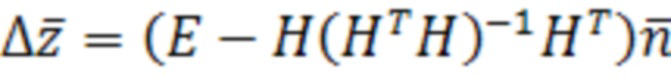 , (7)
, (7)
Геометрический фактор (Dilution of Precision - DOP) представляет собой скалярную величину, описывающую качество геометрического расположения рабочего созвездия НКА, используемого в модели измерений. Различают ряд параметров ухудшения точности, получаемых из элементов главной диагонали (следа матрицы ковариации). Применительно к проблеме контроля целостности измерений ГНСС практический интерес имеют только понятия геометрического фактора ухудшении я горизонтальной точности (Horizontal Dilution of Precision - HDOP) (8) и геометрического фактора ухудшения вертикальной точности (Vertical Dilution of Precision - VDOP) (9), вычисляемые из соотношений:
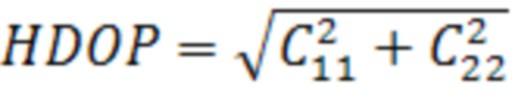 , (8)
, (8)
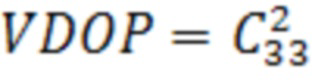 . (9)
. (9)
Все подходы к построению алгоритмов контроля основаны на проверке подмножества частных спутниковых группировок, полученных путем последовательного поочередного исключения каждого НКА из полной группировки. При этом частные геометрический фактор рассматриваемого подмножества имеют меньшую величину по сравнению с общим геометрическим фактором (8) и вычисляются по выражению (10):
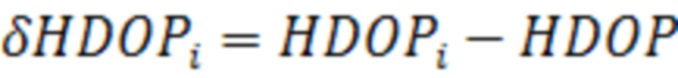 , (10)
, (10)
где 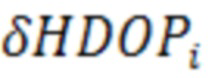 - наибольший из частных HDOP, соответствующий i-му НКА,
- наибольший из частных HDOP, соответствующий i-му НКА,
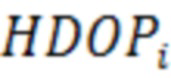 - частный HDOP, вычисленный для i-го НКА.
- частный HDOP, вычисленный для i-го НКА.
Известен способ контроля целостности показаний бортовой аппаратуры глобальной навигационной спутниковой системы [1] (см., Brenner M., Implementation of a RAIM Monitor in a GPS Receiver and an Integrated GPS/IRS, ION GPS-90, Colorado Springs, September 1990) на основе метода равноценных пространств, позволяющем в решении навигационной задачи учесть влияние каждого дальномерного измерения (псевдодальности) до НКА. Для этого выполняется решение системы уравнения (5), описывающих измерения как линейные функции поправок к грубым координатам текущего местоположения.
В выражении (4) содержится дополнительная информация, неучитываемая при оценке координат местоположения классическим МНК. Для выделения этих данных применяется ортогональное преобразование модели, основанное на применении матрицы Q(N×N) (11) такой, что:
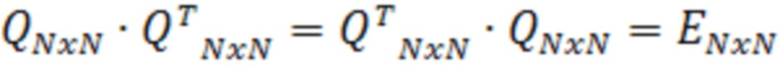 . (11)
. (11)
Матрица Q используется для преобразования матрицы наблюдения H(N×4) в (NxN)-матрицу НПР, содержащую нули в строках с 5 по N, и преобразования в верхнюю треугольную матицу НВТР размерностью (4х4). Модель (4) может быть преобразована следующим образом:
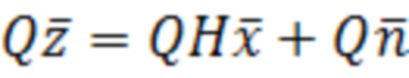 . (12)
. (12)
Матрица Q может быть декомпозирована на две матрицы Q1 и Q2 размерностями (4×N) и ((N-4)×N) соответственно (13):
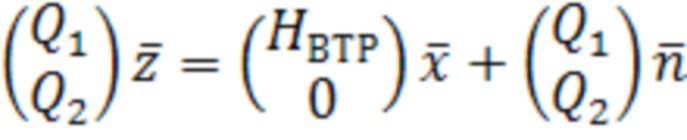 . (13)
. (13)
Рассмотрим вторую строку записанного выше выражения (14):
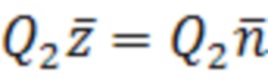 . (14)
. (14)
Искомая метрика D может быть вычислена как (15):
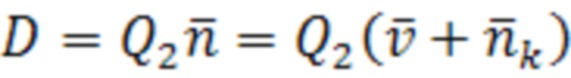 , (15)
, (15)
где 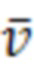 - вектор шумов измерений размерностью N;
- вектор шумов измерений размерностью N;
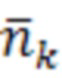 - вектор аномальных составляющих шумов измерений размерностью N, приводящих к отказу.
- вектор аномальных составляющих шумов измерений размерностью N, приводящих к отказу.
Все строки матрицы Q представляют собой ортогональные вектора. Это свойство распространяется и на декомпозированную матрицу Q2. В случае видимости только пят НКА матрица Q2 состоит из одной строки (16):
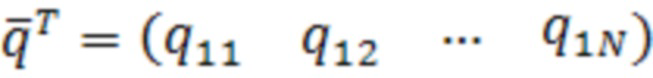 .
(16)
.
(16)
В этом случае искомая метрика D запишется в виде (17):
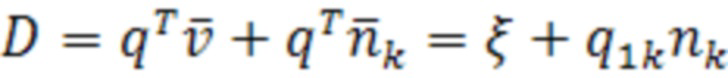 . (17)
. (17)
При этом вектором 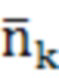 описывается аномальная составляющая шума измерений, приводящих к отказу измерений k-го НКА (18):
описывается аномальная составляющая шума измерений, приводящих к отказу измерений k-го НКА (18):
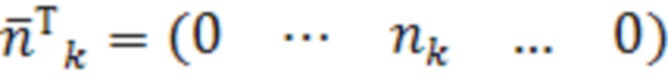 .
(18)
.
(18)
Величина ξ представляет собой скаляр, описывающий нормально распределенную с нулевым математическим ожиданием составляющую шума измерений.
Если вектор измерений имеет размерность большую пяти, то пространство будет многомерным с размерностью (N-4). При этом матрица Q2 будет состоять из (N-4) ортогональных векторов. В введенном пространстве для выявления шумовой составляющей отслеживаемого спутника потребуется рассмотреть только один единичный вектор. Колонка векторов матрицы Q2 определяет влияние ошибок измерения псевдодальностей, разложенных в (N-4) - мерном пространстве, на позиционное решение. В этом пространстве возможно с помощью ортогонального преобразования методом последовательного перебора выбрать такую систему координат, в которой вектор, состоящий из элементов колонки матрицы Q2, соответствующей контролируемому измерению, был бы спроектирован так, чтобы аномальная составляющая ошибки была бы разложена на одну ось. Используемое преобразование не влияет на дисперсию шумов измерений и повышает способность обнаружения ошибки измерений. Обнаружение отказа выполняется по критерию (1).
В случае отсутствия аномальных измерений искомая метрика D = ξ. Граница вычисляется на основе заданной вероятности ложной тревоги 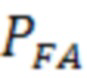 , рассчитываемой из уравнения (19) с применением гипотезы о нормальном законе распределения случайной величины с нулевым математическим ожиданием:
, рассчитываемой из уравнения (19) с применением гипотезы о нормальном законе распределения случайной величины с нулевым математическим ожиданием:
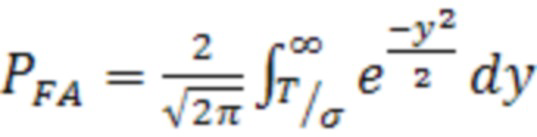 . (19)
. (19)
Если справедлива альтернативная гипотеза (Н1) и k-е измерение содержит аномальную составляющую ошибки, то необходимая для обнаружения отказа величина ошибки измерения nk определяется коэффициентом qk. В этом случае граница вычисляется по выражению (20) на основе заданной вероятности пропуска отказа тревоги 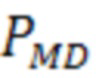 , рассчитываемой из выражения (1) с применением гипотезы о нормальном законе распределения случайной величины с математическим ожиданием, равным (qknk):
, рассчитываемой из выражения (1) с применением гипотезы о нормальном законе распределения случайной величины с математическим ожиданием, равным (qknk):
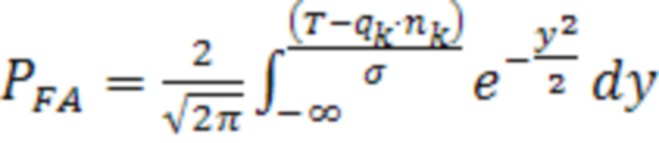 . (20)
. (20)
Наиболее близким по своей технической сущности к заявленному является способ обнаружения отказа, относящийся к первой подгруппе [2] (см., Brown A., Sturza, M., The Effect of Geometry on Integrity Monitoring Performance, Institute of Navigation Annual Meeting, June 1990 https://www.researchgate.net/publication/239926033_The_Effect_of_Geometry_on_Integrity_Monitoring_Performance).
Способ основан на вычислении искомой метрики D на основе квадратичных оценок нормально распределенных невязок измерений. В рассматриваемом подходе для проверки конкурирующих гипотез применяется Хи-квадрат распределение. Вероятность пропуска отказа представляет собой обратную функцию вероятности Хи-квадрат распределения:
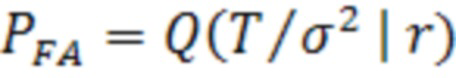 , (21)
, (21)
где 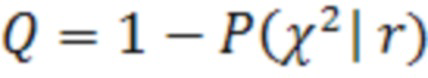 - вероятность обратного события;
- вероятность обратного события;
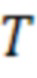 - граница;
- граница;
σ - СКО ошибки определения псевдодальности;
r = (m - n) - число степеней свободы;
n - размерность вектора измерений.
Несмещенная вероятность Хи-квадрат распределения (22) вычисляется следующим образом:
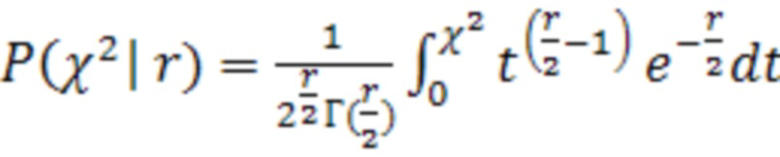 . (22)
. (22)
Граница 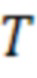 может быть вычислена из обратной функции Q как квантиль Хи-квадрат распределения (23):
может быть вычислена из обратной функции Q как квантиль Хи-квадрат распределения (23):
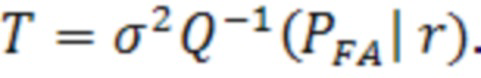 (23)
(23)
Вероятность пропуска отказа (24) рассчитывается на основе выражения:
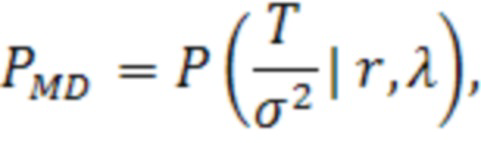 (24)
(24)
где 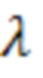 - параметр смещения, вычисляемый на основе выражения (25):
- параметр смещения, вычисляемый на основе выражения (25):
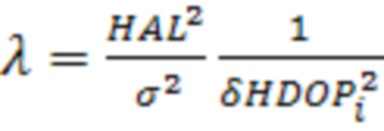 . (25)
. (25)
В соотношении (25) HAL - (Horizontal alarm limit) допустимый уровень ошибки в горизонте, задаваемый согласно требованиям к навигационному обеспечению на данном этапе полета.
Искомая граница 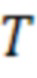 может быть вычислена из уравнения (26), решенного относительно
может быть вычислена из уравнения (26), решенного относительно 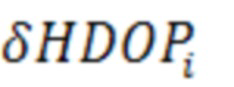 для заданного набора параметров n, σ, HAL,
для заданного набора параметров n, σ, HAL, 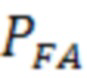 ,
, 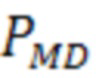 :
:
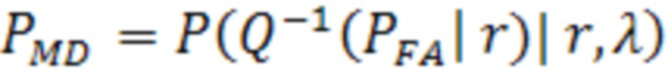 . (26)
. (26)
Существенным недостатком прототипа заключается в использовании в нем только измерений псевдодальностей, измеряемых бортовым оборудованием ГНСС, что накладывает ограничения на доступность реализации алгоритма для решения задачи обнаружения и исключения отказов, возникающих на всех этапах полета условиях недостаточного количества наблюдаемых НКА.
Задача изобретения состоит в решении задачи автономного контроля целостности показаний приемоизмерителя ГНСС и состава бортового оборудования пилотируемых и беспилотных ЛА на всех этапах полета.
Техническим результатом изобретения является расширение функциональных возможностей прототипа за счет повышения доступности его применения на всех этапах полета, включая взлет и посадку, обеспечиваемую за счет привлечения дополнительных измерений, формируемых бортовым алгоритмом счисления координат местоположения курсовоздушным способом.
Сущность изобретения состоит в том, что решение задачи автономного контроля целостности показаний бортовой аппаратуры ГНСС осуществляется с использованием дополнительных измерений от бортового алгоритма курсовоздушного счисления координат местоположения. Способ основан на вводе в алгоритм обнаружения и исключения отказов из показаний приемоизмерителя ГНСС дополнительного дальномерного измерения, сформированного на основе координат местоположения, вычисленных с применением бортового алгоритма курсовоздушного счисления.
В качестве динамической модели системы принимается модель, описанная в (4). Вектор линеаризованных измерений 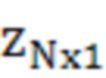 состоит из дальномерных измерений до наблюдаемых НКА и дополнительного дальномерного измерения (27):
состоит из дальномерных измерений до наблюдаемых НКА и дополнительного дальномерного измерения (27):
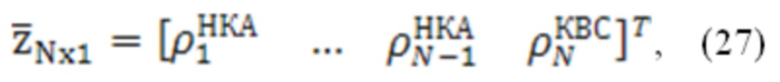
где 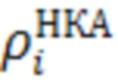 - дальномерных измерений до НКА ГНСС (i = 1 … (N-1));
- дальномерных измерений до НКА ГНСС (i = 1 … (N-1));
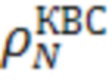 - дальномерное измерение, полученное с использованием курсовоздушного счисления координат;
- дальномерное измерение, полученное с использованием курсовоздушного счисления координат;
N - размерность вектора измерений (общее количество дальномерных измерений).
Дальномерное измерение 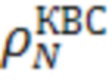 может быть вычислено следующим образом (28):
может быть вычислено следующим образом (28):
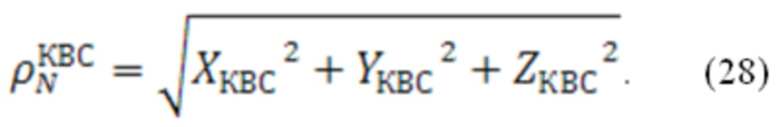
Для приведенного соотношения координаты в геоцентрической системе координат вычисляются по соотношениям (29):
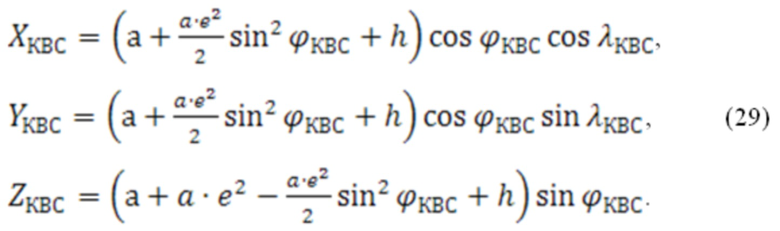
В приведенных соотношениях значение высоты 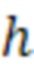 может быть получено на основе барометрического измерения или измерение от других штатных бортовых вычислителей высоты.
может быть получено на основе барометрического измерения или измерение от других штатных бортовых вычислителей высоты.
Матрица наблюдения 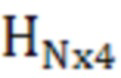 имеет вид (30):
имеет вид (30):
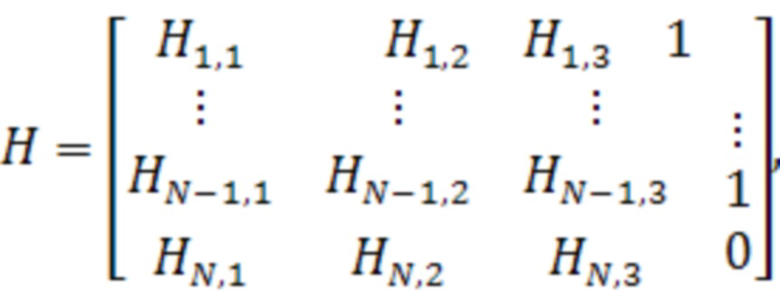 (30)
(30)
Элементы матрицы наблюдения в столбцах с индексами 1, 2 и 3 представляют собой направляющие косинусы линий визирования навигационных объектов: НКА и дополнительного дальномерного измерения.
Вектор нормально распределенных ошибок измерений 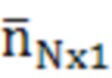 будет содержать СКО ошибок дальномерных измерений до НКА и дополнительного дальномерного измерения, полученного с использованием курсовоздушного счисления координат местоположения (31):
будет содержать СКО ошибок дальномерных измерений до НКА и дополнительного дальномерного измерения, полученного с использованием курсовоздушного счисления координат местоположения (31):
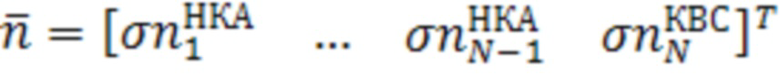 , (31)
, (31)
где 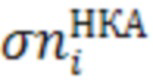 - СКО ошибки дальномерных измерений до i-го НКА ГНСС, (i = 1…(N-1));
- СКО ошибки дальномерных измерений до i-го НКА ГНСС, (i = 1…(N-1));
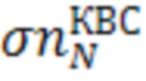 - СКО ошибка дальномерного измерения, полученного с использованием курсовоздушного счисления координат;
- СКО ошибка дальномерного измерения, полученного с использованием курсовоздушного счисления координат;
N - размерность вектора измерений.
Счисление координат местоположения курсовоздушным способом на интервале времени от 0 до T заключается в суммировании начальных координат местоположения 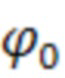 и
и 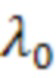 с северной и восточной составляющими приращений координат, вычисляемыми интегрированием северной
с северной и восточной составляющими приращений координат, вычисляемыми интегрированием северной 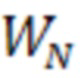 и восточной
и восточной 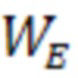 проекций вектора путевой скорости (32):
проекций вектора путевой скорости (32):
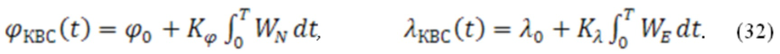
В качестве начальных значений географических координат 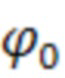 и
и 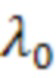 могут быть использованы измерения одной бортовых навигационных систем, включая ГНСС, рассчитанные на предыдущем вычислительном такте.
могут быть использованы измерения одной бортовых навигационных систем, включая ГНСС, рассчитанные на предыдущем вычислительном такте.
Коэффициенты 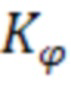 и
и 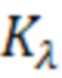 могут быть записаны в виде зависимостей (33):
могут быть записаны в виде зависимостей (33):
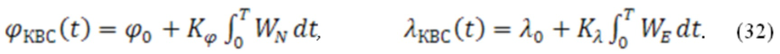
При этом проекции вектора путевой скорости WN и WE вычисляются по соотношениям (34):
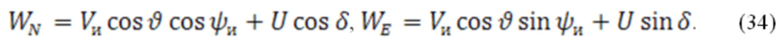
где 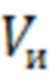 - истинная воздушная скорость, измеряемая СВС,
- истинная воздушная скорость, измеряемая СВС,
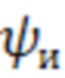 ,
, 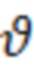 - углы истинного курса и тангажа,
- углы истинного курса и тангажа,
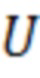 ,
, 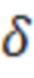 - модуль вектора скорости ветра и угол ветра.
- модуль вектора скорости ветра и угол ветра.
Параметры ветра 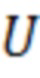 и
и 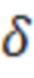 , используемые в соотношениях (34), рассчитываются в соответствии с соотношениями (35 - 40).
, используемые в соотношениях (34), рассчитываются в соответствии с соотношениями (35 - 40).
Модули векторов путевой скорости и скорости ветра вычисляются на основе выражений (35):
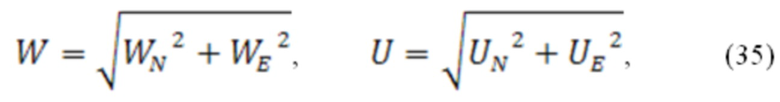
где северная и восточная составляющие модуля скорости ветра определяются соотношениями (36):
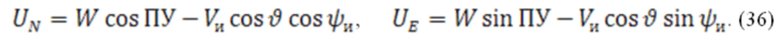
Угол ветра рассчитывается в соответствии со следующим алгоритмом (37):
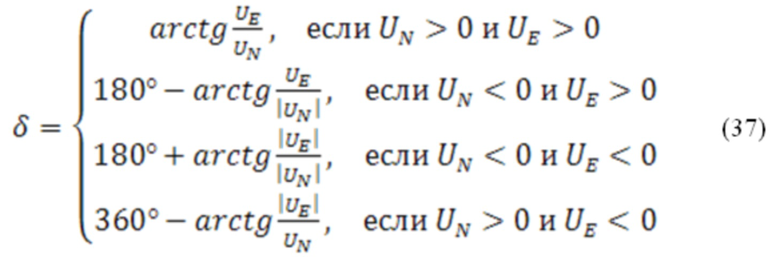
При расчете угла ветра необходимо учитывать особые точки, в которых значение функции арктангенса не определено. В этом случае величина 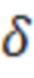 вычисляется по соотношению (38):
вычисляется по соотношению (38):
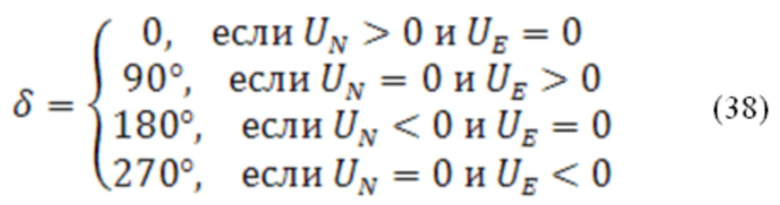
Путевой угол рассчитывается в соответствии с ниже приведенными соотношениями (39):
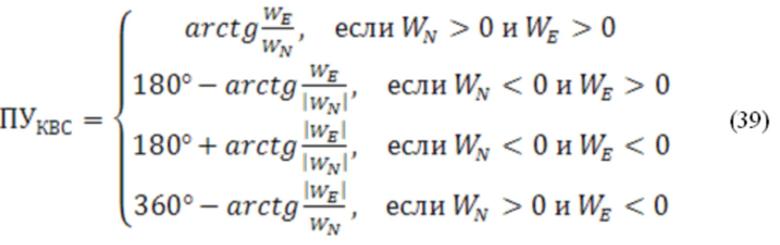
При расчете путевого угла, как и угла ветра, необходимо учитывать особые точки, в которых значение функции арктангенса не определено. В этом случае величина 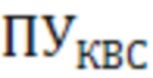 вычисляется по соотношению (40):
вычисляется по соотношению (40):
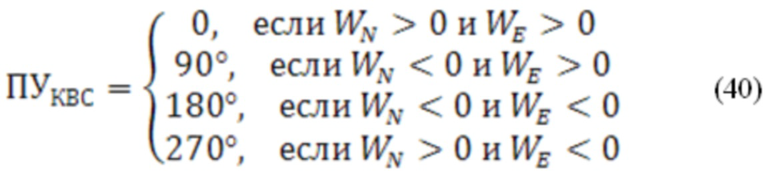
Оценка приведенного вектора состояния выполняется и использованием взвешенного МНК с критерием принятия гипотезы о нормальной работе или отказе, приведенном в (1).
Граница 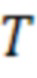 может быть вычислена из обратной функции Q как квантиль плотности вероятности для закона Хи-квадрат (41):
может быть вычислена из обратной функции Q как квантиль плотности вероятности для закона Хи-квадрат (41):
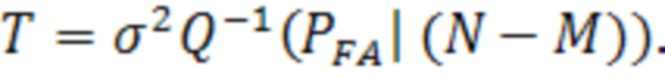 (41)
(41)
Вероятность пропуска отказа рассчитывается на основе выражения (42):
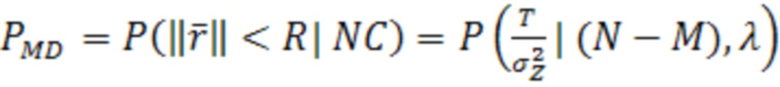 . (42)
. (42)
Параметр смещения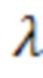 , вычисляемый на основе выражения (24), в котором величина максимальной разности между частными и общим геометрическими факторами
, вычисляемый на основе выражения (24), в котором величина максимальной разности между частными и общим геометрическими факторами 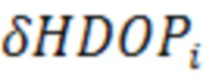 вычисляется на основе соотношения для расчета общего геометрический фактора (43):
вычисляется на основе соотношения для расчета общего геометрический фактора (43):
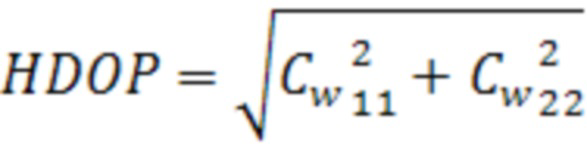 , (43)
, (43)
где 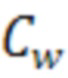 - взвешенная матрица ковариации, вычисляемая как (44):
- взвешенная матрица ковариации, вычисляемая как (44):
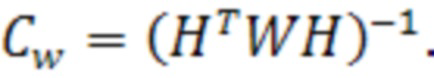 (44)
(44)
Искомая метрика D, используемая в критерии обнаружения отказов (1), может быть вычислена из соотношения (45):
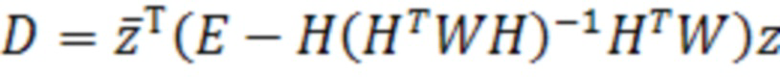 . (45)
. (45)
Процедура идентификации отказа сводится к решению задачи обнаружения отказа для N подсозвездий, полученных из основного созвездия путем поочередного исключения из него каждого j-го НКА для всех j от 1 до N.
Если для общего созвездия отказ обнаружен, но для всех (N-1) частных подсозвездий, не содержащих измерения j-го НКА, отказ не обнаруживается, то НКА с номером j считается отказавшим и исключается из навигационного решения.
Источники информации
1. Brenner M., Implementation of a RAIM Monitor in a GPS Receiver and an Integrated GPS/IRS, ION GPS-90, Colorado Springs, September 1990
2. R. G. Brown and G.Y. Chin, “GPS RAIM: Calculation of Threshold and Protection Radius Using Chi-Square Methods-A Geomet ric Approach,” Navigation, vol. 5, pp. 155-78, Institute of Navigation, 1998
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ и устройство для контроля целостности измерений бортовой аппаратуры глобальной навигационной спутниковой системы (ГНСС) с применением измерений радиосистемы ближней навигации и псевдоспутников | 2021 |
|
RU2778093C1 |
| СПОСОБ ОДНОЧАСТОТНОГО ОПРЕДЕЛЕНИЯ ЗАДЕРЖКИ СИГНАЛОВ НАВИГАЦИОННОЙ СПУТНИКОВОЙ СИСТЕМЫ В ИОНОСФЕРЕ | 2002 |
|
RU2208809C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТОВ-ПОТРЕБИТЕЛЕЙ НАВИГАЦИОННОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2009 |
|
RU2402786C1 |
| Интегрированный комплекс бортового оборудования беспилотного летательного аппарата | 2023 |
|
RU2809930C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ КОСМИЧЕСКИХ АППАРАТОВ | 2004 |
|
RU2275650C1 |
| Способ определения целостности высокоточных навигационных определений в реальном времени | 2017 |
|
RU2644450C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЦЕЛОСТНОСТИ ВЫСОКОТОЧНЫХ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ ПОТРЕБИТЕЛЯ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2014 |
|
RU2577846C1 |
| Способ автономного измерения параметров гравитационного поля на борту космического аппарата | 2022 |
|
RU2784481C1 |
| СПОСОБ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ ИНТЕГРИРОВАННОЙ СИСТЕМЫ ОРИЕНТАЦИИ И НАВИГАЦИИ | 2011 |
|
RU2498335C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ ЭПИЦЕНТРАЛЬНОЙ ЗОНЫ ИСТОЧНИКА И СКОРОСТИ РАСПРОСТРАНЕНИЯ ПЕРЕМЕЩАЮЩИХСЯ ИОНОСФЕРНЫХ ВОЗМУЩЕНИЙ | 2014 |
|
RU2560525C1 |
Изобретение относится к бортовым авиационным навигационным системам, применимым на пилотируемых и беспилотных воздушных судах, в частности к способам обеспечения безопасности эксплуатации пилотируемых и беспилотных летательных аппаратов на всех этапах полета, включая заход на посадку и посадку с использованием системы глобальной навигационной спутниковой системы (ГНСС). Техническим результатом является расширение функциональных возможностей за счет повышения доступности применения способа на всех этапах полета. Заявленный способ заключается в обеспечении контроля целостности показаний бортовой аппаратуры ГНСС с применением метода курсовоздушного счисления координат местоположения летательного аппарата. 2 ил.
Способ контроля целостности измерений авиационных бортовых спутниковых навигационных приемников с использованием дополнительных показаний от бортового алгоритма курсовоздушного счисления координат местоположения, заключающийся в том, что на борту летательного аппарата выполняют непрерывный контроль измерений приемника глобальной навигационной спутниковой системы (ГНСС) для выявления аномальных измерений, приводящих к росту ошибки определения координат, превышающей допустимый уровень, рассчитывают дополнительное дальномерное измерение на основе координат местоположения летательного аппарата, вычисленных курсовоздушным способом счисления, и измерение высоты, полученное штатными бортовыми измерителями, обнаружение отказа в измерениях приемника глобальной навигационной спутниковой системы осуществляют на основе вероятностной проверки гипотезы об отсутствии отказа в измерениях, заключающейся в сравнении искомой метрики D ограничивающей метрикой T, вычисляемой на основе заданной вероятности ложной тревоги, причем искомую метрику вычисляют из соотношения
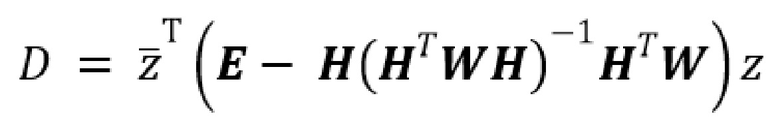 ,
,
где H – матрица наблюдения, элементы которой представляют собой направляющие косинусы линий визирования навигационных космических аппаратов (НКА) и дополнительного дальномерного измерения, z – вектор состояния, состоящий из дальномерных измерений до наблюдаемых НКА ГНСС и дополнительного дальномерного измерения, полученного с использованием курсовоздушного счисления координат, зависящих от измеренного значения высоты, проекции вектора путевой скорости W, истинной воздушной скорости, измеряемой системой воздушных сигналов (СВС), углов истинного курса и тангажа, модулей векторов скорости ветра и угла ветра, при этом обнаружение отказа выполняется по критерию 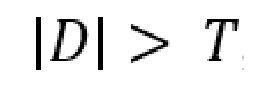 , причем если величина искомой переменной меньше ограничивающей метрики T, то принимается гипотеза о нормальной работе, в противном случае – гипотеза об отказе, при обнаружении отказа в измерениях запускается процедура исключения отказа, заключающаяся в том, что если для общего созвездия НКА отказ обнаружен, но для всех (N-1) частных подсозвездий, не содержащих измерения j-го НКА, отказ не обнаруживается, то НКА с номером j считается отказавшим и исключается из навигационного решения.
, причем если величина искомой переменной меньше ограничивающей метрики T, то принимается гипотеза о нормальной работе, в противном случае – гипотеза об отказе, при обнаружении отказа в измерениях запускается процедура исключения отказа, заключающаяся в том, что если для общего созвездия НКА отказ обнаружен, но для всех (N-1) частных подсозвездий, не содержащих измерения j-го НКА, отказ не обнаруживается, то НКА с номером j считается отказавшим и исключается из навигационного решения.
| Способ выявления неисправностей и отказов бортовых измерителей параметров движения и спутниковых навигационных систем движущихся объектов | 2017 |
|
RU2668597C1 |
| СПОСОБ КОНТРОЛЯ ДОСТОВЕРНОСТИ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ НАВИГАЦИОННОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЯ СПУТНИКОВОЙ РАДИОНАВИГАЦИОННОЙ СИСТЕМЫ ВОЗДУШНОГО СУДНА | 2021 |
|
RU2760345C1 |
| СПОСОБ КОНТРОЛЯ ДАННЫХ ОТ СПУТНИКОВЫХ НАВИГАЦИОННЫХ СИСТЕМ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2015 |
|
RU2585051C1 |
| КОМБИНИРОВАННАЯ СИСТЕМА НАВИГАЦИИ | 2003 |
|
RU2229686C1 |
| КОМПЛЕКСНЫЙ СПОСОБ НАВИГАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2014 |
|
RU2558699C1 |
| WO 2009112483 A1, 17.09.2009 | |||
| РЕГУЛЯТОР ТЕКУЧЕЙ СРЕДЫ, ОБЛАДАЮЩЕЙ УЛУЧШЕННОЙ УСТОЙЧИВОСТЬЮ ПОТОКА | 2013 |
|
RU2614385C2 |
| US 2022065980 A1, 03.03.2022. | |||
Авторы
Даты
2023-10-09—Публикация
2022-07-25—Подача