(Л
с


| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой генератор функций | 1980 |
|
SU980083A1 |
| Устройство для вычисления функций синуса и косинуса | 1980 |
|
SU907546A1 |
| Устройство для вычисления квадратного корня | 1983 |
|
SU1141407A1 |
| Устройство для извлечения корня третьей степени | 1980 |
|
SU903870A1 |
| Цифровой функциональный преобразователь | 1990 |
|
SU1751736A1 |
| Устройство для вычисления функций двух аргументов | 1986 |
|
SU1413626A1 |
| Устройство для вычисления тригонометрических функций тангенса и котангенса | 1980 |
|
SU907545A1 |
| Функциональный преобразователь нескольких переменных | 1986 |
|
SU1387022A1 |
| Устройство для извлечения квадратного корня | 1983 |
|
SU1132289A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ | 2015 |
|
RU2602989C2 |
УСТРОЙСТВО ДЛЯ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ, содержащее счет } 13 Mb4llOi.;,A чик и накапливающий сумматор, отличающееся тем, что, с целью повышения точности, в него введен блок памяти, адресные входы которого соединены с разрядными выходами счетчика, a информационные выходы - с информационными входами накапливающего сумматора, выход переполнения которого соединен со счетным входом двоичного счетчика и входом установки начального кода накапливающего сумматора, тактируюпа1й вход суммирования которого соединен с входом устройства.
со со
со
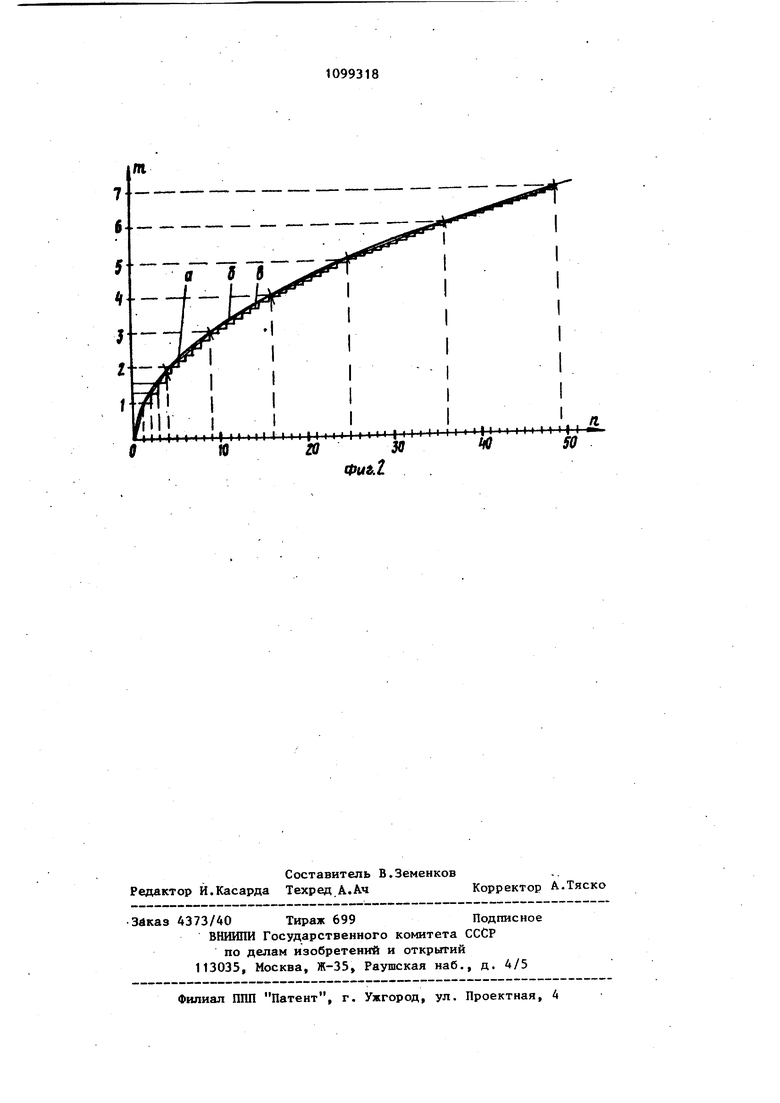
СХ) Изобретение относится к цифровой вычислительной технике и может быть использовано в вычислительных и информахщоно-измерительных устройства Известно устройство для извлечения квадратного корня, работа которого осуществляется за два цикла. Во время первого цикла на устройств поступает число П , представленное число-импульсном коде, и определяет ся целая часть результата вычислений с недостатком. По окончании пос тупления числа Ц устройство перехо дит ко второму циклу, во время кото рого по значению остатка аргумента с домощью кусочно-линейной интерполяхщи определяется приближенное з значение дробной части результата вычислений m. Недостатками данного устройства является сложность и низкое быстродействие. Наиболее близким по технической сущности к предлагаемому является устройство, содержащее счетчик, накапливающий сумматор, генератор . импульсов, схему совпадения и две группы схем считывания, пр1и этом прямые выходы всех разрядов счетчика через первую группу схем считывания подсоединены к вьпсодам устройства, а через вторую группу схем считывания - к информационным входам накапливающего сумматора,вы ход переполнения которого соединен общим тактируюпдам входом схем считы вания первой группы, а выход знаков го разряда - с первым входом схемы совпадения, второй вход которой соединен с выходом генератора.импуль- до сов, а выход - со счетным входом счет чика и общим тактируюпщм входом схем считывания второй группы, входы установки начального кода накапливающего сумматора подсоединены к входам устройства. Данное ,устройство обеспечивает целочисленное извлечение квадратного корня rtln из произвольного числа Пц с абсолютной погрешностью, максим альное значение которой равно Недостатком данного устройства является погрешность, составляющая .nor ловину младшего разряда целочисленного результата вычислений. Цель изобретения - повьшение точности устройства. Указанная цель достигается тем, что в устройство для извлечения квадратного корня, содержащее счетчик и накапливающий сумматор, введен блок памяти, адресные входы которого соединены с разрядными выходами счетчика, а информационные выходы с информационными входами накапливающего сумматора, выход переполнения которого соединен со счетным входом двоичного счетчика и входом установки на чал ьного кода накапливающегосумматора, тактирующий вход суммирования которого соединен с входом устройства. На фиг. 1 представлена структурная схема устройства; на фиг. 2 графики, поясняющие принцип его работы. Устройство содержит счетчик 1, блок 2 памяти, накапливающий сумматор 3, вход 4. При этом выходы разрядов счетчика 1 подсоединены к адресным входам блока 2 памяти. Информационные выходы блoka 2 памяти соединены с информационными входами накапливающего сумматора 3. Тактирующий вход суммирования сумматора 3 соединен с входом 4 устройства. Выход переполнения сумматора 3 соединен со счетным входом счетчика 1 и входом установки начального кода сумматора 3. В основу алгоритма работы устройства положены следующие соображения . На фиг. 2 представлены кривая а,, соответствующая истинному значению функции m 4F , график- б, задающий кусочно-линейное .приближение данной функгдаи, и кусочно-ступенчатая ломаная в, описывающая поведение кусочно-линейного приближения при целочцсленйых значениях аргумента. Как следует из соотношения () + 2mt1 очередные целочисленные значения аргументов, при которых формируются целочисленные значения функции, различаются на величину 2Ш-1, что )ц О, 1, 2, 3, 4... дает ряд нечетных чисел 1,3,5,7,9... . Если при очередных значениях |1ц , заключенных в интервале между значениями hi.j, которым соответствуют целочисленньге значения Шц,-, задавать функции m приращения, равные .тг-гэ :С2.) то будет формироваться кусочно ступенчатая функция (график Ь на фиг. являющаяся дискретным аналогом кусочно-линейного приближения (график 5 на фиг. 2). Так, например, на ин тервале изменения аргумента от 1 до 4 необходимо значению функции задавать приращения - на интервале от 4 до 9 I и т.д. Для формирования об ратных значений нечетных чисел целе сообразнее использовать блок памяти табличного принципа действия на основе ПЗУ или комбинационных логических устройств с зашитой функци |ей преобразования. Потребную информационную емкость блока памяти определяют следующим образом. Если максимально возможное значе ние числа h равно N, т.е. динамический диапазон аргумента составляе jlogjNt К двоичных разрядов, гдеЗС ближайшее большее целое чи ло, то число адресных входов блока памяти равно числу разрядов счетчик целой части функции Шц, а именно Г р. Разрядность выходных слоев блока памяти определяется тре буемой погрешностью вычисления. Наи более типична ситуация, при которой приведенную погрешность результата вычислений необходимо иметь равной или близкой к приведенной погрешнос ти задания аргумента. Число значащих разрядов функ151И принимают при этом равным числу значащих разрядов аргумента. В данном случае это приводит к необходимости иметь дробную часть результата извлечения квадрат ного корня с числом разрядов, ранНЫМ:1Ео,, , И абсолютной погрешностью 2 . Определяют общее число разрядов накапливающего сумматора, обеспечивающее данную погрешность определения дробной части. Обозначают его равным В , чему соответствует абсолютная погрешность задания слггае wbix t 2 . Приращения функции In с блока памяти поступают на младшие разряды сумматора. Как известно, при многократном суммировании равноточных чисел абсолютная погрешность возрастает в q раз, где q число суммирований. При извлечении квадратного корня по указанному алгоритмуНмакс 2-цма.(2Р-1).1о 2 2, следовательно, абсолютная погрешность достигает величины .,f. , Требуют, чтобы эта погрешность не превьш1ала величины 2 , т.е. , откуда K +1. Таким образом, при равенстве числа разрядов аргумента и функции накапливающий сумматор должен иметь не менее (К+1) разрядов, из которых (k-p) разрядов отводится для дробной части результата вычислений. Если учесть, что максимально возможное число, подаваемое на накапливающий сумматор, равно V которое в двоичном представлении имеет старшую значащую цифру во втором разряде после запятой, то число значащих разрядов выходного слова блока памяти достаточно иметь равным , т.е. равным рДзрядности аргумента. Необходимая информационная емкость I блока памяти составляет при этом 2 Ч - разрядных слов. Так, например, при k 8, Р 4, 3 16-8 12в бит; а при .с 16, Р 8, 3 256- 16 4096 бит, что соответственно в 16 или 256 раз меньше, чем при использовании чисто табличных методов вычисления с такой же приведенной погрешностью и не представляет трудностей для практической реализации на современной микроэлектронной элементной базе. Помимо инструментальной составляющей погрешности, обусловленной ограниченной разрядностью представления результата вычислений, при кусочно-линейной интерполяции имеет место и методическая составляющая погрешности. Для ее оценки уравнение аппроксимирующей кусочно-линейной функции для каждого i -го участка интерполяции имеет следующий вид. . ...i u.i + .,i Откуда приПц- Шц, имеем . im, + t Методическаяпогрешность интерполяции, аналитическое выражение для которой имеет вид rti i(3 имеет отрицательный знак и достигае на каждом 4 -ом участке интерполяци своего максимального по модулю значения, равного иметдда с1%( . Как показывает анализ, при вычислении функции с приведенной погрешностью равной погрешности задания аргумента, уже на интервалах интерполя1.щи с номерами .8 2 - IJ - максимально возможное число участков интерполяции, методическая составляющая погрешнос ти уменьшается настолько, что выход за пределы разрядной сетки. Так, например при К 8 уже на втором участке интерполяции (от П 4 до 9) методическую погрешность можно не, учитывать, при К 16 методическая погрешность уходит за пределы разрядной сетки на участках интерполяции, начиная с 32-го и далее. В любом случае практически динамического диапазона воз можных значений аргумента влиянием методической погрешности можно пренебречь. При равенстве числа значащих разрядов аргумента и функции приведенная погрешность вычислений данного устройства по сравнению с прототипом уменьшается в 2/2 -И 2-1 раз. Так, например, при k 8 и при К 16 выигрыш в точности составляет соответственно 8 и 128 раз. Устройство для извлечения квадратного корня работает следующим образом. В исходном положении все разряды счетчика 1 установлены в нулевое, а все разряды накапливающего сумматора 3 - в единичное состояние. На выходах блока памяти присутству код, содержащий во всех разрядах единицы. Число, из которого извлекается квадратный корень, подается в число-импульсном коде на вход 4 устройства. При поступлении первог импульса на тактирующий вход суммирования накапливающего сумматора, он переполняется и импульс переполнения передается на счетчик 1 . В счетчике устанавливается код коэффициента наклона первого участка интерполяции. Импульс переполнения поступает также на вход установки начального кода сумматора. Начальный Код сумматора содержит нулевые значения во всех разрядах, отведенных для дробной части результата вычис. лений. и единичные значения во всех остальньк разрядах. Начальная предустановка сумматора необходима для обеспечения его переполнения при Поступлении последнего на данном интервал,е приращения функции с одновременным сохранением в заданных пределах максимальной приведенной погрешности вычислений. По мере поступления последующих импульсов входного кода к начальному содержимому сумматора добавляются коды, формируемые блоком 2 памяти на первом участке интерполяции и равные /5 , пока не сформируется второе переполнение. Код счетчика 1 становится равным двум, на выходе блока 2 памяти устанавливается код, равный /5, в сумматоре 3 устанавливается значение начального кода и при поступлении последующих импульсов входной последовательности формируются значения результата вычислений на втором участ ке интерполяции. В дальнейшем работа устройства осуществляется аналогично. Периодическая установка начального кода в накапливающем сумматоре при достижении аргументом значения очередного узла и-нтерлоляции исключает накопление инструментальной погрешности. В (К - Р) старших разрядах сумматора формируются достоверные значащие цифры дробной части результата вычислений, а в счетчике формируется код целой части. Технико-экономический зффект от использования предлагаемого изобретения заключается в том, что благодаря сочетанию итерационного алгоритма вычисления целой части результата с таблично-алгоритмическим принципом формирования его дробной части существенно повьш1ается точность устройства при сравнительно небольших дополнительных аппаратурных затратах.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Устройство для извлечения квадратного корня | 1976 |
|
SU641449A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| 1971 |
|
SU413479A1 | |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1984-06-23—Публикация
1980-05-28—Подача