Изобретение относится к автоматическому управлению и регулированию и, преимущественно, может быть использовано для стабилизации и последовательного управления конечны состоянием широкого класса объектов с переменными пар аметрами и неконтролируемыми -ёозмущениями.
Цель изобретения - уменьшение энегетических зат1р гна управление.
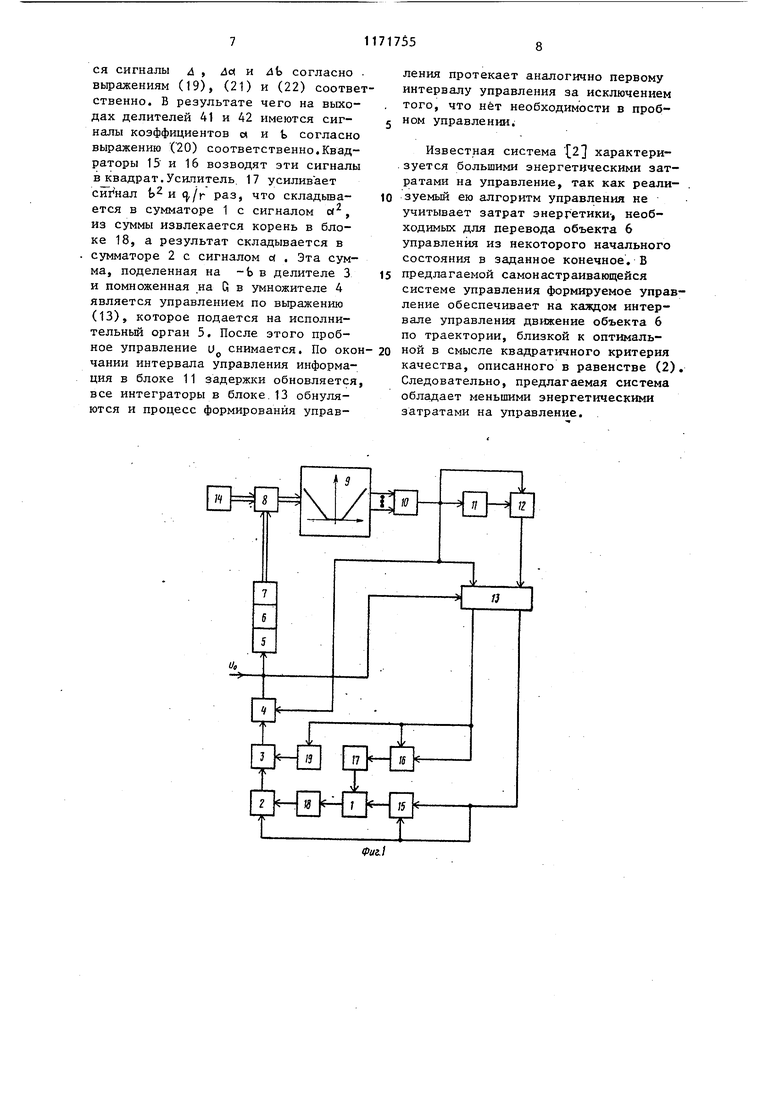
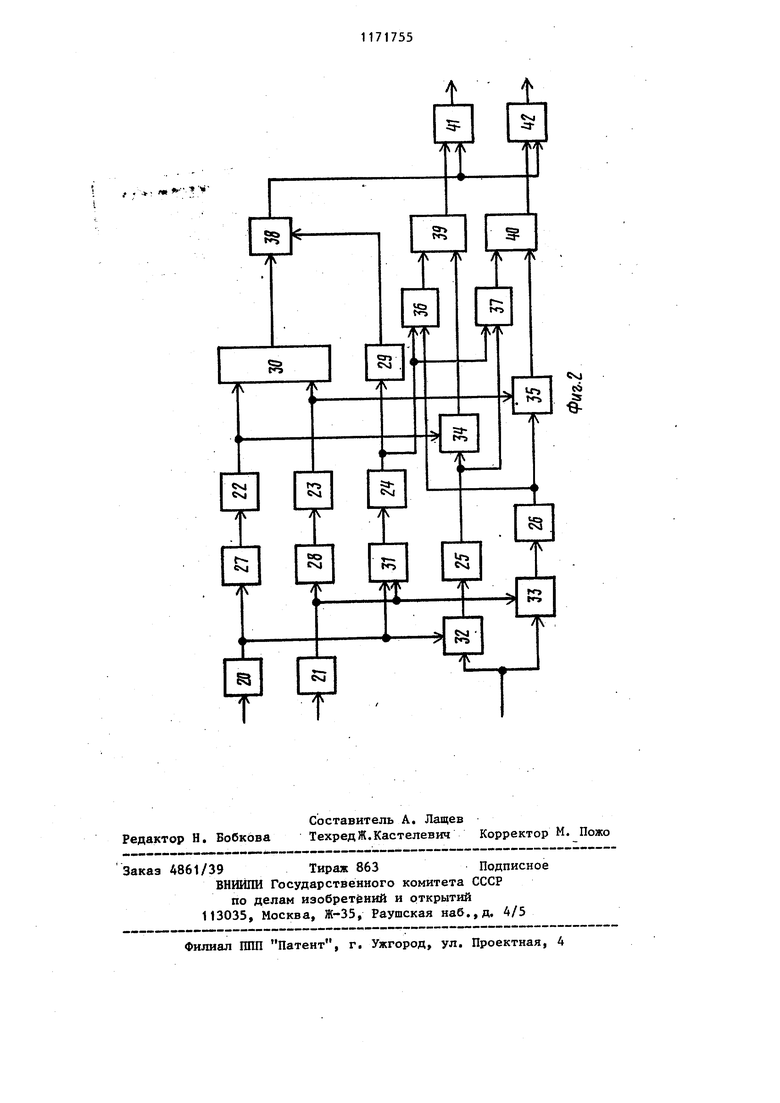
На фиг. 1 представлена структурмая схема ,пй1 длага;емой системы; на фиг. 2 - внутрен-няя структура блока решения системы уравнений.
Самонастраивающаясясистема , управления содержит, (фиг. 1) первый сумматор 1, последовательно соединенные второй сумматор 2, блок 3 деления, блок 4 умножения, исполнительный орган 5, объект 6 управления измерительное устройство 7, первый блок 8 сравнения, функциональный преобразователь 9, третий сумматор 1 блок 11 задержки, второй блок 12 сравнения и блок 13 решения системы уравнений, задатчик 14, выход которого связан с втррьш входом первого блока 8 сравнения, первьм квадратор 15, выход которого соединен с первым входом первого сумматора 1, второй квадратор 16, выход которого через усилитель 17 соединен с вторым входом первого сумматора 1, блок 18 опрделения квадратного корня, вход которого соединен с выходом первого сумматора 1, а выход - с вторым входом второго сумматора 2, и инвертор 19, выход которого соединен с вторым входом блока 3 деления. Первый выход блока 13 решения системы уравнений соединен с первым и вторым входами первого квадратора 15 и с первым входом второго сумматора 2,- а второй его выход соединен с первым и вторым входами второго квадратора 16 и входом инвертора 19, выход блока 4 умножения связан с вторым входом блока 13 решения системы уравнений, выход третьего сумматора 10 связан с вторыми входами второго блока 12 сравнеПИЯ и блока 4 умножения и с третьим входом блрка 13 решения системы уравнений.
Последний может быть выполнен по, любой известной схеме. Например, блок 13 (фиг. 2) состоит из семи интеграторов 20-26, трех блоков 27-29 степени, восьми умножителей 30-37,
трех блоков 38-40 сравнения и -двух делителей .41 и 42. Входы интеграторов 20 и 21 являются соответственно третьим и вторым входами блока 13, входы умножителей 32 и 33 собраны в одну точку и являются первым входом блока 13. Выходы делителей 4 и 42 являются соответственно первым и вторым выходами блока 13. Интегратор 20, блок 27 степени и интегратор 22 соединены последовательно и подключены к первому входу умножителя 30.
Интегратор 21, блок 28 степени и интегратор 23 соединены последовательно и подключены к второму входу умножителя 30, выход которого подключен к первому входу 28 сравнения Дыходы интеграторов 20 и 21 подключены к входам умножителей 31 и соотвётственно вторым входам умножителей .32 и 33. Выход умножителя 31 через интегратор 24 и блок 29 степени подключен к второму входу блока 38 сравнения, выход которого подключен к первым входам делителей 41 и 42. Выходы умножителей 32 и 33 через интеграторы 25 и 26, умножители 34 и 35 подсоединены к первым входам блоков 39 и 40 сравнения соответственно. Выход интегратора 24 подключен к первымвходам умножителей 36 и 37, к вторым входам которых подключены выходы интеграторов 26 и 25 соответственно. Выходы интеграторов 22 и 23 подключены к вторым входам умножителей 24 и 25 соответственно. Выходы умножителей 36 и 37 подключены к вторым входам блоков 39 и 40 сравнения соответственно, выходы которых подключены к вторым вхо-дам соответственно делителей 41-и 42.
Работа предлагаемой системы поясняется с помощью теоретических выкладок.
Пусть объект управления описывается векторным-дифференциальным уравнением вида
х(х,и, t); х(Ц)Хо,
(1)
где X - п -мерньй вектор фазовых
координат;
D - скалярное управление; i - время.
Пусть вид зависимости (1) неизвестен. Необходимо найти такое управление u{.t) (teftjit, которое переводи объект, описанный уравнением (1), из начального состояния Xj, в заданное конечное состояние Xi. и при это минимизирует функционал качества (x ax+ru)c/t, (2) где Q - неотрицательно-определенная матрица; fjO - скаляр; Т - знак транспонирования. Вводят отображение из пространства фазовых координат объекта по урав нению (1) на вещественную прямую R вида Gtx) (x.,-xr) , о, hii, (-Г) о, .| ; Ui,n Функция С(( равна О в -окрестности точки х и равна сумме модулей отклонений фазовых .координат от их заданных конечных значений, уменьшенных на Е , вне этой окрестности. Следовательно, G(x ) - неотрицательная вьшуклая функция, имеющая на фазовом пространстве единственньй минимум, равньй нулю и достигаемьш на -окре сности: точки х. Так как любое управление u(t) порождает в силу уравнения (1) некоторую фазовую тра екторию x(i), ) то это управление порождает и некоторую траекторию ((i), -и (t) на R в силу равенства (3) Последнюю называют отображенным движением и описывают дифференциальным уравнением вида G, , Q(XO)G где а, Ъ- скалярные коэффициенты. Для простоты дальнейших выкладок принимают, что в выражении (2) матрицы Q Ё , где С),- скаляр, а единичная матрица. Тогда функционалу качества по уравнению (2) в фазовом пространстве можно поставить в соответствие функционал качества в отображенном пространстве Н ) , (М А 554 Если значение можно сделать сколь угодно малым, то поставленная задача эквивалентна следующей: найти управление и уравнение (1), переводящее отображенный объект, описанный равенством (5), из начального состояния QP в конечное состояние Q j О и при этом минимизирующее функционал качества,.описанный в уравнении (6). Сформулированная задача легко решается, если известны коэффициенты « и Ь выражения (5). Допустим, что они известны, тогда для нахождения управления записывают уравнение Беллмана .(o,)0, ( где 5(G) - функция Беллмана. Очевидно, что управление, минимизирующее выражение в фигурных скобках, имеет вид - G Подставив е;го в уравнение (7), получаютi,,.i.f4lf.4l-«G o. 2 Чйй/ Г.2 аа функцию Беллмана ищут в виде 5lG)ikQ Подставив уравнение (10) в равенство (9) и проделав элементарные преобразования, получают . --2k«-c 0, Oi) откуда Ь2/г а управление f с,+ atVr Доставленная задача решена. Для нахождения коэффициентов а и Ь выражения (5) разбивают все время на интервалы управления длительностью Т и определяют коэффициенты е и Ь для каждого интервала управления.Для этого проинтегрировав выражение (5) в пределах одного интервала управления teCOiJ получают I uCt)).GcJ(«G(u(r)Mt. С14) J Искомые коэффициенты находят из ус вия минимума функционала Г I(t)«i (uGCc)-j(aGWbtuCi/l)cfi/f . В результате получают систему уравt i UQCT)Ucif)IVdtrr uol.i/) о о 00 itr t tU«G(.4Wi uWcl4dlV, 10 « tr J (i HVclr- uCi)c/V uCtfWVd 6 0 ALswicit/ ui idi d 1дС(Г)аСГ)(с(ГН ф{Г|Ь(Г); 000 Jf, UG(f|D(r)(trlO(irlcir bpT), Г иС)оСЧ), S((4)c/V. ii6) 00 . Главный определитель системы (17) « G DMt uH lolt-JuCtlGCrlc/f 5 оо xG(t)uC)c/r , откуда as- , -г ил . .,Uci(.r|GCt c r D4)cltr- u(tlQCtr))tr« AGUIDCrjcif , о . i GVMt:54B(t)u(t),/r-LGtr)QCt|d я V о5 GCtlGltjcIt . .(i2) Зная, таким образом, для любого момента teCOT) интервала управления коэффициенты с( и Ъ , можно определить управление, выраженное равенством (13). Для начала процесса задается некоторое пробное управление Uc . Предлагаемая система работает следующим образом (фиг. 1). В начальньй. момент времени измерительный орган 7 определяет текущее значение фазового вектора . х , которое сравнивается в блоке 8 с заданным конечным значением Х|, , поступающим из задатчика 1А. Разность Xfc-X поступает в функциональный преобразователь 9, где по каждой фазовой координате разность х i преобразуется согласно выражению (4), характеристика такого преобразования изображена (фиг. 1) в поле блока 9. В результате на каждом выходе блока 9 имеются сигналы выражения (4) , ..которые суммируются в сумматоре 10, на выходе которого имеется функция Q(x) выражения (3). Значение Ci(x) в начальный момент запоминается в блоке 11 задержки. В этот же момент на вход исполнительного органа 5 подается пробное управление и, под действием которого объект 6 изменяет свое состояние X и изменяется функцией Q(x) fta выходе сумматора 10. Текущее значение G(x) поступает на входы блока 13, блока 12 и умножителя 4. Б блоке 12 сравнения, текущее значение Q( х) сравнивается с начальным G(0) и их разность dG (t) поступает на первый вход блока 13, на вход которого поступает сигнал Up. Блок 13 осуществляет решение системы уравнений (16) по информации о G(i) , 4G(i)H Uj . При этом (фиг.2) на выходе блоков 38 - 40 формируются сигналы 4 , 4с( и лЬ согласно вьфажениям (19), (21) и (22) соотве ственно. В результате чего на выходах делителей 41 и 42 имеются сигналы коэффициентов с и Ь согласно выражению (20) соответственно.Квадраторы 15 и 16 возводят эти сигналы в квадрат.Уси.питель, 17 усиливает и cj,/r раз, что складьшается в сумматоре 1 с сигналом и , из суммы извлекается корень в блоке 18, а результат складывается в сумматоре 2 с сигналом л , Эта сумма, поделенная на -Ь в делителе 3 и помноженная на G в умножителе 4 является управлением по выражению (13), которое подается на исполнительньй орган 5, После этого пробное управление и снимается. По око чании интервала управления информация в блоке 11 задержки обновляется все интеграторы в блоке.13 обнуляются и процесс формирования управления протекает аналогично первому интервалу управления за исключением того, что нет необходимости в пробном управленииi Известная система характеризуется большими энергетическими затратами на управление, так как реали- зуемый ею алгоритм управления не учитывает затрат энергетики-, необходимых для перевода объекта 6 управления из некоторого начального состояния в заданное конечное. В предлагаемой самонастраивающейся системе управления формируемое управление обеспечивает на каждом интервале управления движение объекта 6 по траектории, близкой к оптимальной в смысле квадратичного критерия качества, описанного в равенстве (2), Следовательно, предлагаемая система обладает меньшими энергетическими затратами на управление.


| название | год | авторы | номер документа |
|---|---|---|---|
| Система автоматического управления | 1984 |
|
SU1168897A1 |
| Устройство для идентификации параметров систем управления | 1979 |
|
SU885976A1 |
| Адаптивная система управления | 1987 |
|
SU1464139A1 |
| Коррелятор | 1991 |
|
SU1798803A1 |
| Квазиоптимальная по быстродействию система управления | 1981 |
|
SU987575A1 |
| Устройство формирования программы кинематического разворота твердого тела | 1989 |
|
SU1659979A1 |
| АДАПТИВНАЯ СИСТЕМА ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ | 2012 |
|
RU2500009C1 |
| Устройство для решения задач оптимального управления | 1985 |
|
SU1327135A1 |
| Адаптивная система управления | 1980 |
|
SU980070A1 |
| Система последовательного финитного управления конечным состоянием линейных стационарных динамических объектов | 1987 |
|
SU1467534A1 |

САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ, содержащая первьй сумматор, второй сумматор, блок деления, блок умножения и последовательно соединенные исполнительньй орган, объект управления, измерительное устройство, первьш блок сравнения, функциональный преобразователь,третий сумматор, блок задержки, второй блок сравнения и блок решения системы уравнений, второй вход первого блока сравнения соединен с выходом задатчика, выход третьего сумматора соединен с вторым входом второго -блока сравнения, отличающаяся тем, что, с целью уменьшения энергетических затрат на управление, система содержит первый квадратор, второй квадратор, усилитель, блок определения квадратного корня и инвертор, первьй выход блока решения системы уравнений подключен к первому и второму входам первого квадратора и через второй сумматор , блок деления и блок умножения к входу исполнительного органа и второму входу блока решения системы уравнений, второй выход которого соединен с первым и вторым входами (Л второго квадратора и через инвертор с вторым входом блока деления, выход первого квадратора соединен через первьй сумматор и блок определения квадратного корня с вторым входом второго сумматора, выход второго квадратора через усилитель соединен с вторым входом первого сумматора, выход третьего сумматора соединен с третьим входом блока реше СП ел ния системы уравнений и с вторым входом блока умножения.
, . ,
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Солодовников В.В., ШрамкоЛ.С, Расчет и проектирование аналитических самонастраивающихся систем с эталонной моделью | |||
| - М: Машиностроение, 1972, с | |||
| Стиральная машина для войлоков | 1922 |
|
SU210A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Авторское свидетельство СССР по заявке № 3697672/24, кл | |||
| Кипятильник для воды | 1921 |
|
SU5A1 |
Авторы
Даты
1985-08-07—Публикация
1984-02-23—Подача