ОБЫЧНО вычисление координат равноотстоящих точек окружности при необходимости сочетания высокой точности получаемых координат с возможностью произвольного выбора величины углового приращения между равноотстоящими точками требует использования формул, для реализации которых в специализированном вычислительном устройстве приходится иметь большое число составных элементов, -причем время вычислений получается сравнительно большим.
Предлагается способ вычисления координат точек окружности {с центром в начале координат) по реккурентным формулам:
Х(л+1)Х(л)()+У(п) .2-м У(п+1)У(п)(1-2-«-1)+Х(п)
(здесь 2 ; cos ад, где ш-постоянное угловое приращение, а к-произвольно выбираемое целое положительное число).
Предлагаемое устройство, работающее в двоичной системе счисления, получается достаточно простым и обладает сравнительно высоким быстродействием, так как операция умножения сводится в основном к одному сдвигу. Соответствующим выбором величины к и числа ис пользуемых в устройстве двоичных разрядов можно получить любую практически необходимую точность.
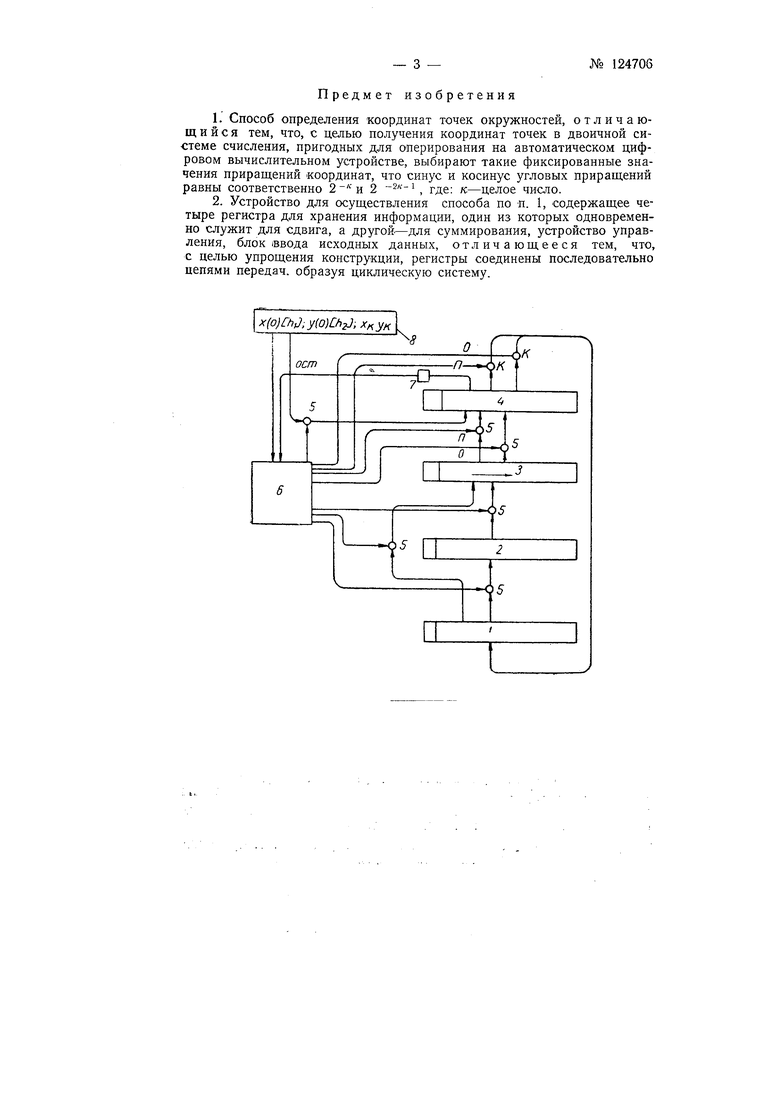
В блок-схему устройства, показанную на чертеже, входят четыра двоичных регистра: регистры / и 2 служат для хранения информации, в регистре 3 производится требуемый сдвиг чисел, а регистр 4 является сумматором параллельнрго действия и осуществляет сложение чисел. Передача двоичных чисел через клапаны 5 прямым (Я) или обратным
(О) кодом производится при помощи сигналов передачи, вырабатываемыми устройством управлепия б, которое состоит из тактового генератора счетчика и логических диодпых. схем. Устройство предназначено для управления объектами, в которых требуется осуществлять движение по контуру, состоящему из дуг окружностей и отрезков прямых линий. Число отрезков может быть произвольным. Координаты точек прямой вычисляются по формулам
X(n+)X(n}+h, I ,,
У()У(/г)+Ъ2 I
где hi и /Z2-заранее вводимые постоянные числа (приращения). При отработке прямолинейного отрезка его начало совпадает с началом координат (Х(0) У(0) 0), в случае дуги окружности начало координат переносится условно в центр окружности. В качестве управляющих сигналов устройство вычисляет и выдает приращения координат
Х(п + 1)Х(п + 1)-Х(п) I ДУ(п+1)У(л + У)У(п) I (
Концом отрезка (прямолинейного или криволинейного) является точка Хк , УК , для обнаружения подхода к которой устройство вычисляет и сравнивает с нулем веллчииы
Х,.(п) I
У. -У(л) j
При подходе к концу отрезка выдаются последние разности (4), благодаря чему отсутствует накопление погрешности из отрезка в отрезок, и на выходе логической схемы «И 7 вырабатывается сигнал остановки «ост.
Начальные данные Х{0); У(0); Хк ; УК (или hi; hz; Хк ; УК ) вводятся с вводного устройства 5 с помощью перфокарт в регистр-. Кроме того, с ВВОДНОГО устройства 8 вводится величина к и признак «прямая-окружность. В течение всего времени вычислений, связанных с одним отрезком, информация, относящаяся к этому отрезку, стоит в вводном устройстве 8.
Порядок вычислений для случая окружности показан в таблице.
.Регистры

| название | год | авторы | номер документа |
|---|---|---|---|
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ДЛЯ СИСТЕМ | 1969 |
|
SU257150A1 |
| ЛИНЕЙНО-КРУГОВОЙ ИНТЕРПОЛЯТОР | 1972 |
|
SU332438A1 |
| Способ определения длины отрезка | 1989 |
|
SU1783271A1 |
| Устройство для формирования дуг и окружностей на экране телевизионного индикатора | 1990 |
|
SU1800476A1 |
| Способ пассивной однопозиционной угломерно-доплеровской локации перемещающихся в пространстве радиоизлучающих объектов | 2019 |
|
RU2699552C1 |
| Устройство для контурного управления промышленным роботом | 1984 |
|
SU1211691A1 |
| Интерполятор | 1978 |
|
SU798729A1 |
| Линейно-круговой интерполятор | 1985 |
|
SU1259218A1 |
| СПОСОБ КОРРЕКЦИИ ЭКВИДИСТАПТЫЙСЯСОЮЗНАЯ^ • .'*"v-' - -"••;v-||Ap|, . ) .-il : Jb ' , ., •:, .^ -tltit'',b:-u.:^;-;o,,:^KA ( | 1971 |
|
SU295113A1 |
| Многокоординатный линейно-круговой интерполятор | 1984 |
|
SU1156008A1 |

Принцип данного устройства может быть использован для управления движением не только по плоским, но и по пространственным кри ВЫМ. - .
Авторы
Даты
1959-01-01—Публикация
1958-05-17—Подача