ю
О) ел
сх. Изобретение относится к аналоговой вычислительной технике, предназ начено для решения систем алгебраических уравнений и может служить основой для создания специализированных аналоговых процессоров гибридных вычислительных комплексов., Целью изобретения является повышение точности и расширение функцио нальных возможностей устройства за счет учета дополнительной априорной информации о гладкости решения. На фиг.1 представлена блок-схем устройства; на фиг.2 - блок-схема блока управления. Устройство содержит три матрицы 1-3 токозадающих резисторов, коммутатор 4, блок 5 интеграторов, блок 6 -вычитаталей, первый блок 7 формирователей модуля сигнала, второй блок 8 формирователей модуля сигнал первый и второй блоки 9 и 10 суммирования, блок 11 управления и блок 12 задания начальных условий. Блок 11 содержит блок 13 умножения, сумматор 14 и компаратор 15. Устройство работает следуюпдам ,образом. Три матрицы 1-3 токозадающих резисторов моделирунл- расширенную матр цу коэффициентов системы А, матрицу коэффициентов А, транспонированную к А, и матрицу коэффициентов С соответственно. На входы блока 11 управления поступают сигналы, соответствующие числовым параметрам oi и /3 , характеризующим погрешности в коэффициентах матрицы А и правых частей Ь соответственно. Приближенное, устойчивое решение решаемой системы линейных алгебраических уравнений образуется на выходе блока 5 интеграторов . Предлагаемое устройство описывается системой обьжновенных дифференциальных уравнений с постоянны ми коэффициентами и некоторьми начальными условиями:
1/h
О
О
О
О
-1/h О
О
О
1/h -1/h ОО
О1/h -1/hО
001/h-l/h
0001/h + . х(о) Опишем подробно функции каждого из блоков, входящих в предлагаемое устройство. Матрица I предназначена для умножения вектора x(t) на матрицу А и вычитания вектора правой части Ь, т.е. матрица 1 представляет собой резистивную матрицу, на вход которой поступают сигналы X|(t), i 1,2,..., n, являющиеся компонентами п мерного вектора x(t) x,(t)x(t),..., x(t) , а на выходе образуются сигналы ri(t), i ,2,..., п, являющиеся компонентами вектора невязки r(t) Ax(t)-b, r(t) г, (t) r(t),..., i,(t). Матрица 1 резисторов.осуществлЯг ет умножение невязки r(t) на матрицу А , т.е. на вход , указанного блока поступают компоненты вектора r(t), а на выходе формируются компоненты вектора g(t) (t) Ax(t) - Ab. На выходах матрицы 3 резисторов djrltl формируются сигналы f(t) dt посредством решения уравнения «.(t)), на ее первую группу входов поступают сигналы g(t) с выхода матрицы 2, а на вторую группу входов - сигналы С выходов матрицы 3 резисторов. Матрица С образуется путем перемножения матрицы D на D, где матрица D осуществляет преобразование вектора U(v) на сетке с шагом h в производную J--- . dv
1/h -1/h
С i 0 r 0
0 0
Элементы C матрицы С принимают значения
если 1i-j , ,5
С;; О,
с;; -l/h , если 1 i-j 1 1,
2/h , если i 2,...,
п - ,
«2
Cj; 1/h , если i I,п.
Отметим, что матрица С имеет ленточную структуру с шириной ленты, равной трем.
. Блок II управления служит для проверки условия
//r(t)// (A,(t)-b//fo //x(t) - x,//-t- /J,(2)
где // // - норма вектора; ot и /3 числовые параметры, определяющие
Если llrll Up(y//x - yij/+ р , то и - О,
если llrll
Таким образом, при выполнении ус ловия //г//4«//х - XQ// +/3 блок управления формирует сигнал U 1, который размыкает ключи коммутатора 4.
В целом устройство опнсьюается системой дифференциальных уравнений (1). Решение этой системы дифференциальных уравнений в установившемся состоянии есть нормальное решение исходной системы линейньк алгебраических уравнений относительно вектора Хд. При Хд О модель позволяет получить решение с минимальной нормой в пространстве Wj функций, имеющих обобщенную производную, интегрируемую с квадратом.
В исходном состоянии на выходах интеграторов блока 5 интеграторов установлены напряжения, соответствуmmyie априорно известному вектору х, определяемому постановкой задачи.
-1/h ОО
2/h -l/h ОО
-1/h 2/h -1/h О
О-1/h 2/h -1/h
ОО-1/h 1/h
погрешность задания исходных данных //4 Д //4 ci ; //дЬ //s ; л А и fib - погрешности задания матрицы А и вектора правых частей Ь соответственно. Сигнал
и, //X(t) - X // i:/X;(t) - i«l
перемножается на oi на блоке 13 и складьшается с /3 на сумматоре 14. На выходе сумматора образуется сигнал «; // X - + ft , который с помощью компаратора I5 сравнивается с сигналом
и, // r(t)// «i/r;(t)/.. .
В зависимости от соотношения сигналов И ио //х-х,у/ +А блок II управления вырабатывает сигнал управления U , который поступает на управляющий вход коммутатора 4.
xj/ +р , то и « 1.
В процессе интегрирования системы обыкновенных дифференциальных уравнений (1) с помощью блоков 1-5 на выходах блока 6 непрерывно образуется вектор разности x(t) - х, на выходах блока 7 - вектор, компонентами которого являются модули вектора X(t) - Х, т.е. /X;(t) - Х,/,
на выходе блока 9 - напряжение, соответствующее норме //x(t) - Хд// вектора x(t)-x. На выходах блока 8 непрерывно образуется вектор, ксмпоненты которого являются модулями (t)/ вектора невязки v(t), на выходе блока 10 - напряжение, соответствующее норме //г (t)//, вектора r(t). Здесь и далее
U,(t)// -Г /г;а)/, . т.е. используется вторая норма вектора . В блоке II управления реализуется проверка согласованности получаемого решения с погрешностью исходных данных в соответствии с условиями (2 При вьшолнении указанного неравенства блок II управления на выходе формирует сигнал иа размыкание ключей коммутатора 4. При этом на выходе блока 5 фиксируются напряжения, соответствующие устойчивому приближению к решению исходной системы линей ных алгебраических уравнений. Таким образом, предлагаемое устройство для решения систем линейных алгебраических уравнений позволяет автоматически получать приближенное устойчивое решение поставленной задачи с большей точностью за счет учета имеющейся априорной информации о гладкости решения. Отметим, что при условии точного задания коэффициента матрицы А и вектора правых частей Ь предлагаемое устройство реализует метод установления в чистом виде и позволяет получить нормальное репюние алгебраической системы, такое же как и известное устройство. В процессе интегрирования системы дифференциальных уравнений (1) в предлагаемом устройстве норма вектора (tb//(I + с) V/ монотонно уменьшается от некоторого .начального значения, определяемого невязкой исходной системы алгебраических, уравнений при X XQ, до нуля при t- с (если с OJ. Одновременно норма вектора z(t) //(I+c)x(t)//, как интеграл от Zj(t) монотонно увеличивается от некоторо го начального значения 2г(о) , //(I+c)Xjj//до конечного значения при . Таким образом, если исходные данные известны приближенно, т.е. х. 0 f f Of остановив процесс интегрирова ния при некотором t t , согласно условиям (2), на выходе блока 5 интеграторов формируется приближенное устойчивое решение поставленной зада чи, у которого минимальна функция 2j;(t) //(I+c)x(t)// . Таким образом формируется прибл)1жеи}юе решение системы линейных алгебраических уравнений, обладающее минимальной длиной, и одновременно минимальной нормой первой производной, характеризующей гладкость решения. Следовательно, предлагаемое устройство позволяет, в отличие от известного сформировать приближенное устойчивое решение, обладающее минимальной длиной и наиболее гладкое одновременно, тем самым достигается поставленная цель расширения функциональных возможностей устройства за счет учета дополнительной априориой информации о гладкости решения, одновременно удается повысить точность решения. Предлагаемое устройство позволяет решать не только плохо обусловленные , но и хорошо обусловленные алгебраические системы. Формула изобретения Устройство для решения систем линейных алгебраических уравнений, содержащее блок задания начальных условий, первую и вторую матрицы токозадающих резисторов, блок интеграторов, первый и второй блоки формирователей модуля сигнала, группы выходов которых подключены к группам входов соответственно первого и второго блоков суммирования, коммутатор, блок управления и блок вычитателей, группа выходов которого соединена с группой входов первого блока формирователей модуля сигнала, группа выходов блока задания начальных условий подключена к входам задания начальной установки блока интеграторов и к первой группе входов блока вычитателей, вторая группа входов которого соединена с группой выходов блока интеграторов и с выводами первой группы токозадающих резисторов первой матрицы, вьюоды второй группы которых подключены к группе входов второго блока формирователей модуля сигнала и к выходам первой группы токозадаюш 1х резисторов второй матрицы, группа выходов коммута-. тора соединена с группой информационных входов блока интеграторов, отличающееся тем, что, с целью повьшзения точности, в него введена третья матрица токозадающих резисторов, а блок управления состо71ит из компаратора, сумматора и блоха умножения, выход которого подключен к первому входу сумматора, выход которого соединен с первые входом компаратора, выход которого подключен к управляющему входу коммутатора, информационный вход которого сов единен с выводами первой и второй групп токоэадающих резисторов третьей матрицы, выводы третьей группы токозадающих резисторов третьей матрицы соединены с выводами второй 1 Q гpyiaibi токозадакяцих резисторов второй матрицы, вход задания погрешности матрицы постоянных коэффициентов системы уравнений устройства подключен кпервому входу блока умножения, второй вход которого соединен с выходом первого блока суммирования, вход задания погрешности вектора правых частей системы уравнений устройства соединен с в то рьм в ход ом сумма- ,тора,выход второго блока суммирования подключен к второму входу компаратора.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования систем линейных алгебраических уравнений | 1976 |
|
SU612258A1 |
| Устройство для решения операторных уравнений | 1978 |
|
SU763921A1 |
| Устройство для решения систем линейных алгебраических уравнений | 1984 |
|
SU1187157A1 |
| Устройство для решения систем алгебраических уравнений | 1984 |
|
SU1320820A1 |
| Система последовательного финитного управления конечным состоянием линейных стационарных динамических объектов | 1987 |
|
SU1467534A1 |
| Устройство для решения системы алгебраических уравнений | 1981 |
|
SU966702A1 |
| Система идентификации параметров линейных объектов | 1988 |
|
SU1534429A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ ОБЪЕКТА ПРИ ИСПОЛЬЗОВАНИИ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СПУТНИКОВЫХ СИСТЕМ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2492499C1 |
| Устройство для решения систем линейных алгебраических уравлений | 1972 |
|
SU564638A1 |
| Устройство для решения линейных интегральных уравнений (его варианты) | 1985 |
|
SU1278899A2 |
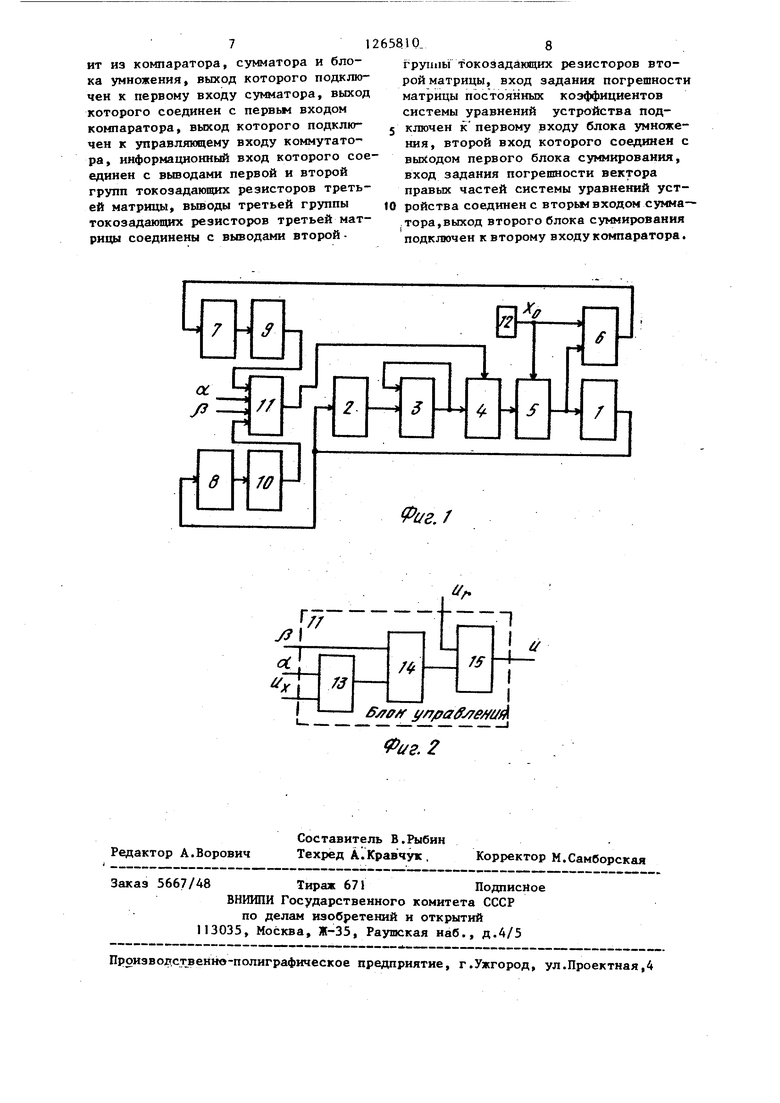
Изобретение относится к аналоговой вьиислительной технике и предназначено для решения систем линейных алгебраических уравнений. Устройство содержит три матрицы токоэадающих резисторов, блок задания начальных условий, коммутатор, блок вычитаталей, два блока формирователей модуля сигнала, два блока суммирования, блок интеграторов, блок управления. Устройство позволяет решать системы линейных алгебраических уравнений с приближенно заданными исходньми данными при наличии апри(Л орной информации о гладкости решения . 2 ил. с
.2

| Математическое моделирование и теория электрических цепей; Сб | |||
| Вып | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Фальцовая черепица | 0 |
|
SU75A1 |
| Устройство для моделирования систем линейных алгебраических уравнений | 1976 |
|
SU612258A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1986-10-23—Публикация
1985-03-01—Подача