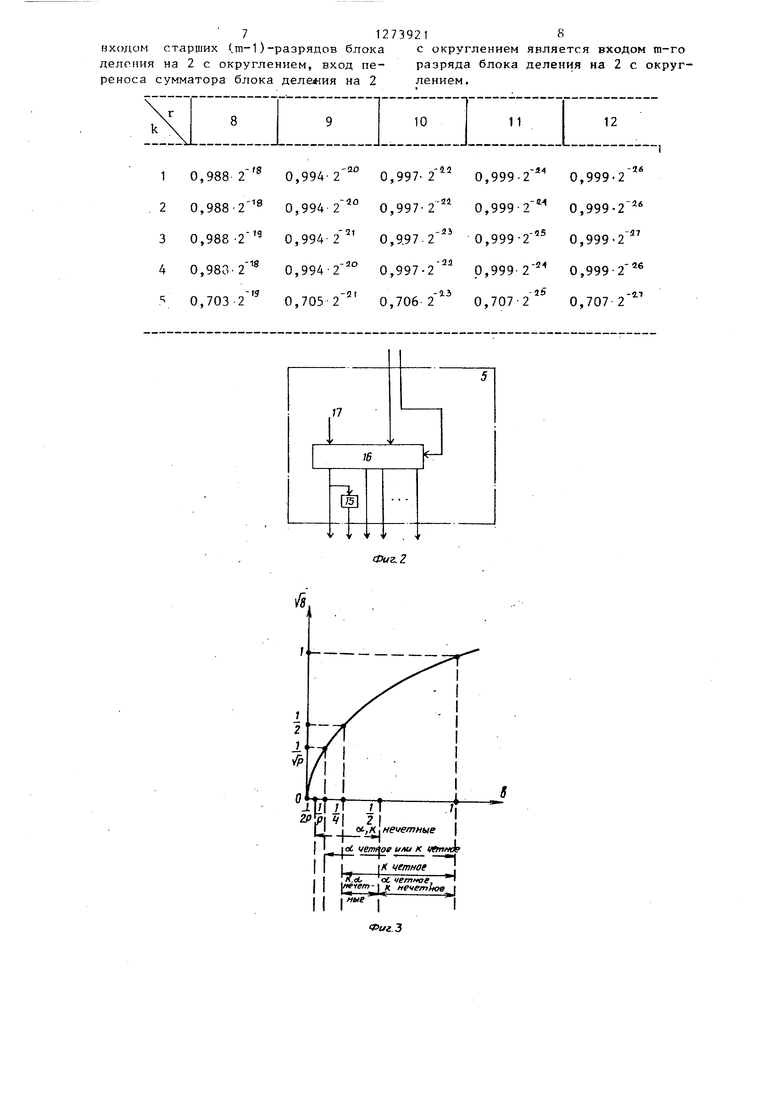
1 Изобретение относится к вычислительной технике и может быть использовано в составе арифметико-логических устройств ЦВМ, а также в виде самостоятельного вычислительного уст ройства. Цель изобретения - повышение быстродействия и расширение функциональ ных возможностей, заключающихся в обеспечении, возможности извлечения квадратного корня из числа с плавающей запятой, где Р - основание системы счисления ( , ,2,...); oL- порядок, представленный m двоичными разрядами; а - мантисса, представленная п двоичными разрядами. На фиг. 1 представлена блок-схема устройства; на фиг. 2 - схема блока деления на 2 с округлением; на фиг.З график функции квадратного корня; на ,фиг. 4 - линейная интерполяция функции квадратного корня. Устройство (фиг. 1) содержит первьш и второй блоки 1 и 2 постоянной памяти, входной и выходной сдвигател 3 и 4, блок 5 деления на 2 с округле нием, дешифратор 6, вход 7 младшего разряда порядка аргумента, умножител 8, сумматор 9, вход 10 старших разрядов порядка аргумента, выход 11 порядка результатаJ вход 12 старших разрядов мантиссы аргумента, вход 13 мпадших разрядов мантиссы аргумента, выход. 14 мантиссы результата. Блок 5 деления на 2 с округлением (фиг. 2) содержит элемент НЕ 15, сум матор 16, шину 17 логического нуля. Устройство функционирует следующи образом. Результат операции извлеченяя квадратного корня можно представить: , где С - результат операции; f- - порядок результата; с - мантисса результата; А - исходное число (); а - мантисса числа А (а.1-2 m - разрядность порядка о(. ,J. Значение можно представить в следующем виде: г- 2гДЛЯ четного ot: i/a; - . для нечетного « : 1 1 /Г , /I f , - /F/n Причем для четных k можно записать к. Л-й. /а-2 2. соответственно для нечетных k: гвенно fl-ff. VP Y2 На фиг. 3 показан график функции (Ь) (Ь - число на выходах входного сдвигателя 3), в соответствии с которым в устройстве производится вычисление величины Гь. В предложенном устройстве при вычислении величины /Ь производится замена кривой Л прямолинейным отрезком (см. фиг. 4) в каждом диапа °.,i - i-n - 0,1,...). Вычисление vb производится в соответствии с соотношением , L, где &Ь Ь-Ь, ; h - цена младшего разряда числа г причем величина уЬ выдается из блока постоянной памяти, величина д. fb. -/Ъ- вьщается из второго блока 2 по стоянной памяти, умножение дЬ- на Af- производится в умножителе 8 (деление лЬ af- на h означает- просто перенос запятой), а окончательное сложение - в сумматоре 9. Блок 5 деления на 2 с округлением вычисляет порядок , а остальные узлы - мантиссу с. Правила работы устройства формулируются следующим образом: Y т при четном oi ; оС + 1 при нечетном «L ; 2tГ , при четном о ; c,/b-f при нечетном ц ct-и чётном k; 2f-i г- Т , при нечетных с/ и. Здесь 1 - количество пар нулей между запятой и старшей единицей в числе а. Очевидно, что 1 может принимать значения п . k-2 , 0,1,... ,о при четном k; k-1 0,1,...,--- при нечетном k. Детали формирования порядка у гут несколько видоизменяться в за симости от формы представления по ка и от конкретной реализации бло о5 деления на 2 с округлением. На фиг. 2 показана одна из возможных реализаций. Она предполагает след щую, наиболее распространенную фор представления порядков: Порядок Представлени 11...111 2 -1 -2 1 1 . ..110 10...oil 10. . .010 10...001 10...000 01 . ..111 01 . ..1 10 00...001 .00.. .000, m разрядов Если, например, ci +3 , то поряд f, равный , формируется след щим образом (см. фиг. 2): 1 00. ..01 - входы второго слагаем сумматора 16 + 1 - вход 1 переноса сумма тора 16 €00...00 - входы 17 первого слага мого сумматора 16 1 00...00 - выходы сумматора 16 1000...10 - выходы блока 5 деления на 2 с округлением (Y m разрядов Если, например, , то О 11 ...10 + О О 00...00 О 11...10 0111...10 (). Дешифратор 6 служит для управле входным 3 и выходным 4 сдвигателям и строится по соотношениям (1). В упрощенном варианте устройств (см. фиг. 1, без учета связи, пока занной пунктиром сдвигатель 3 сдвигает величину а вправо на один разряд (при нечетных k,) или на Ноль разрядов (в остальных случаях), на блоках 1 и 2, умножителе 8 и сумматоре 9 вычисляется величина /г (при нечетных k,ot) или Va (в остальных случаях), а сдвигатель 4 сдвигает эту величину вправо на --- разрядов (при нечетных kai) или на разрядов (оС- нечетное, k - четное), или на ноль разрядов (aL- четное). Таким .образом, в упрощенном варианте устройства система уравнения (1) заменяется на при четномс ; при нечетном и четЬ |; cWb.f ° при нечетныхы и k. На фиг. 3 показаны диапазоны изменения b для упрощенного и полного (фиг. 1) вариантов устройства соответственно пунктирными и сплошными линиями. Входной сдвигатель 3 под управлением дешифратора 6 (фиг. 1) сдвигает мантиссу а влево на 21-1 разрядов при нечетных k,oi и на 21 разрядов во всех остальных случаях. Полученное после сдвига число лежит в диапазоне - 2-. 2f 2 2 1-2 при четном k; 2 1-2 при нечетном k и четном 0 ; .2 - 2- -2при нечетных k, ы . Поскольку при величина 1 равна улю, то в этом частном случае входой сдвигатель 3 не нужен (формально удем считать, что он есть и осущестляет сдвиг на разрядов). После олучения на выходах сумматора 4 веичины /Ь она сдвигается вправо на: разрядов при четномс/-; + . разрядов при нечетном Ы и четном k; r-+Р разрядов при нечетных k,oC. В устройстве погрешность вычислеия величины N/A складывается из меодической погрешности (связанной с аменой кривой (Ь) набором прямоинейных отрезков) и аппаратной порешности, связанной с ограниченной разрядностью чисел, выдаваем1 1х блоками 1 и 2 постоянной памяти, и аппаратными погрешностями умножителя 8 и сумматора 9. Назовем величину дЫ-Af; 5 (, -V ) методической погрешностью аппроксима ции величины Л. Пусть - максимальное значение (, величины О в диапазон .,, , а - максимальное значение методической погрешности аппроксимации величины /Ь во всем диапазоне изменения Ъ: .(Л17Т il i ±J JL14i i 4(7F,,, Щг iib kulb SiIll - в таблице приведена зависимость максимальной методической погрешнос от г и k с учетом сдвига, производи мого в выходном сдвигателе 4. Отметим, что методическая погреш ность устройства уменьшается в два раза, если, не изменяя величин f- , хранящихся во втором блоке 2 постоя ..ной памяти, хранить в первом блоке постоянной памяти вместо величин где b- b.+ih; ,1,...) величины sfbr+-s.. Формула изобретения 1 . Устройство для извлечения квад ратного корня, содержащее первый и второй блоки постоянной памятии сумматор, причем вход первого слагаемого сумматора подключен к выход первого блока постоянной памяти, от личающееся тем, что, с цель повЬппения быстродействия и расширен функциональных возможностей, заключающихся в обеспечении возможностей извлечения корня из числа а с плаваклцей запятой, где Р - основани системы счисления (, ,2,3,. ..) ct- порядок, представленньй m двоич ными разрядами; а - мантисса, предоставленная п двоичными разрядами, в него дополнительно введены дешифратор, входной и выходной сдвигатели, блок деления на 2 с округлением и умножитель, причем выход умножителя подключен к входу второго слагаемог сумматора, вход первого сомножителя умножителя подключен к выходу второго блока постоянной памяти, вход второго сомножителя умножителя - к (п-г)младшим разрядам вьгхода входного сдвигателя (где п - разрядность мантиссы аргумента; г - разрядность адреса в первом и втором блоках постоянной памяти), входы адреса первого и второго блоков постоянной памяти к г старшим разрядам выхода входного сдвигателя, выход сумматора - к информационному входу выходного сдвигателя , информационный вход входного сдвигателя является входом мантиссы аргумента устройства, выход выходного сдвигателя - выходом мантиссы результата устройства, вход блока деления на 2 с округлением - входом порядка аргумента устройства, выход блока деления на 2 с округлением - выходом порядка результата устройства, вход дешифратора подключен к младшему разряду входа блока деления на 2 с округлением, первый выход дешифратора подключен к входу управления входного сдвигателя, а второй выход - к входу управления выходного сдвигателя. 2.Устройство по П.1, о тли чающееся тем,что,с целью повышения точности, старшие К-1-(при нечетном К) или К-2 (при четном К)разряды входа мантиссы устройства соединены с дополнительным входом дешифратора. 3.Устройство по пп. 1 и 2, о т .-. личающееся тем, что блок Деления на 2 с округлением содержит . сумматор и элемент НЕ, вход которого подключен к выходу старшего разряда сумматора блока деления на 2 с округлением, старший разряд выхода сумматора блока деления на 2 с округлением является первьм разрядом выхода блока деления на 2 с округлением, выход элемента НЕ - вторым разрядом выхода блока деления на 2 с округлением, j-й (,3,..., m-1; где m разрядность порядка аргумента) разряд выхода сумматора блока деления на 2 с округлением является (j+1)-M разрядом выхода блока деления на 2 с округлением, первый информационный вход сумматора блока деления на 2 с округлением подключен к шине логического нуля устройства, второй информационный вход сумматора блока деления на 2 с округлением является
712739218
входом старших (m-l)-разрядов блока с округлением является входом т-го деления на 2 с округлением, вход пе- разряда блока деления на 2 с округреноса сумматора блока делелия на 2 лением.


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения обратной величины числа /его варианты/ | 1984 |
|
SU1246090A1 |
| Устройство для вычисления синуса | 1986 |
|
SU1319025A1 |
| Устройство для вычисления косинуса числа | 1988 |
|
SU1522197A1 |
| Устройство для вычисления элементарных функций | 1983 |
|
SU1160454A1 |
| Устройство для вычисления показательной функции | 1988 |
|
SU1536376A1 |
| Устройство для накопления чисел с плавающей запятой | 1990 |
|
SU1829030A1 |
| Устройство для вычисления квадратного корня | 1984 |
|
SU1191908A1 |
| Специализированный процессор | 1983 |
|
SU1144117A1 |
| Устройство для вычисления элементарных функций | 1983 |
|
SU1160429A1 |
| Специализированный процессор | 1977 |
|
SU734705A1 |
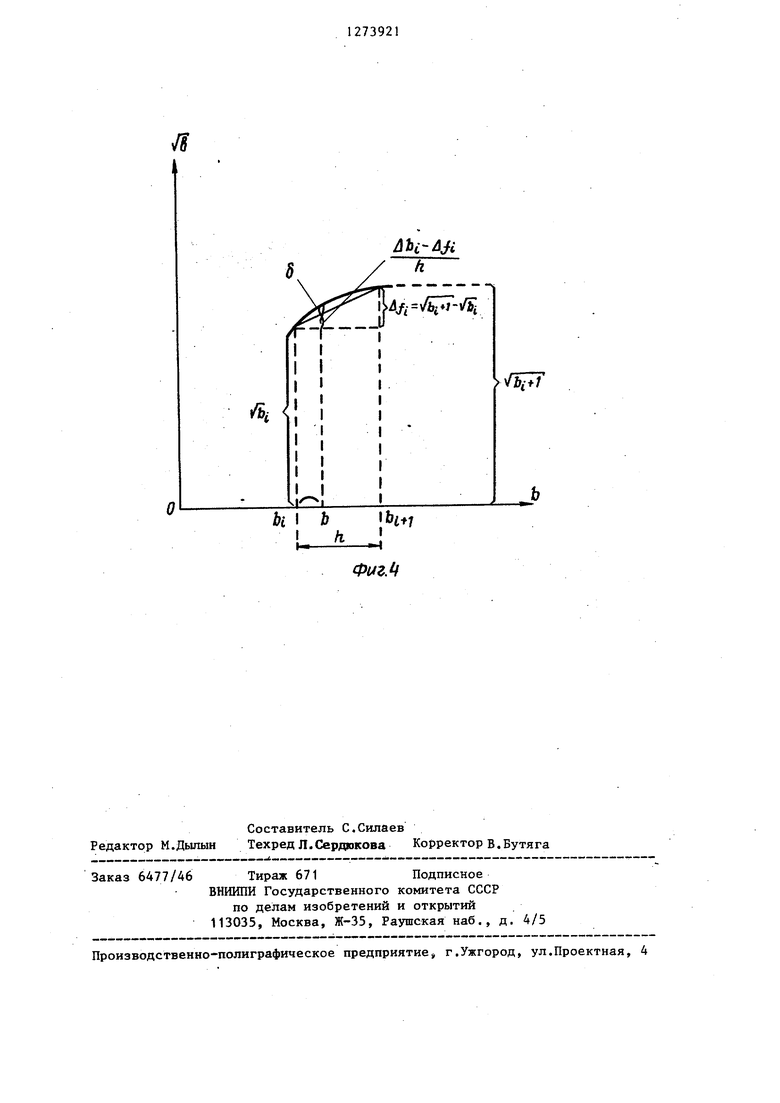
Изобретение относится к вычислительной технике и может быть использовано в составе арифметико-логических устройств ЦВМ, а также в виде самостоятельного вычислительного устройства. Целью изобретения является повышение быстродействия и расширение функциональных возможностей, заключающихся в обеспечении возможности извлечения квадратного корня из числа А Р а с плавающей запятой, где Р- основание системы счисления (, k 1,2...); с.- порядок, представленный m двоичными разрядами; а - мантисса, представленная п двоичными разрядами. Устройство содержит блоки 1 и 2 постоянной памяти, сдвигатели 3 и 4, блок 5 деления на два с округлением, дешифратор 6, вход 7 мпадшего разряда порядка . аргумента, умножитель 8, сумматор 9, вход 10 старших разрядов порядка арс S гумента, выход 11 порядка результата, вход 12 старших разрядов мантиссы аргумента, вход 13 мпадших разрядов мантиссы аргумента, выход 14 мантиссы результата. 2 з.п. ф-лы, 4 ил., 1 табл. 00 со ю
Abi-A i
fb
ФигМ
| Устройство для извлечения квадратного корня | 1982 |
|
SU1089578A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Hemel А | |||
| Square Root Extraction with Real-Only memories.- Computer Design, April, 1972, p.100-104. | |||
Авторы
Даты
1986-11-30—Публикация
1984-06-15—Подача