Устройство относится к вычислительной технике и может быть использовано в составе цифровых вычислительных машин, предназначенных для решения задач с комплексными числами в области электроэнергетики, связи, гидродинамики.
Цель изобретения - расширение класса решаемых задач за счет обеспечения возможности умножения комплексных чисел.
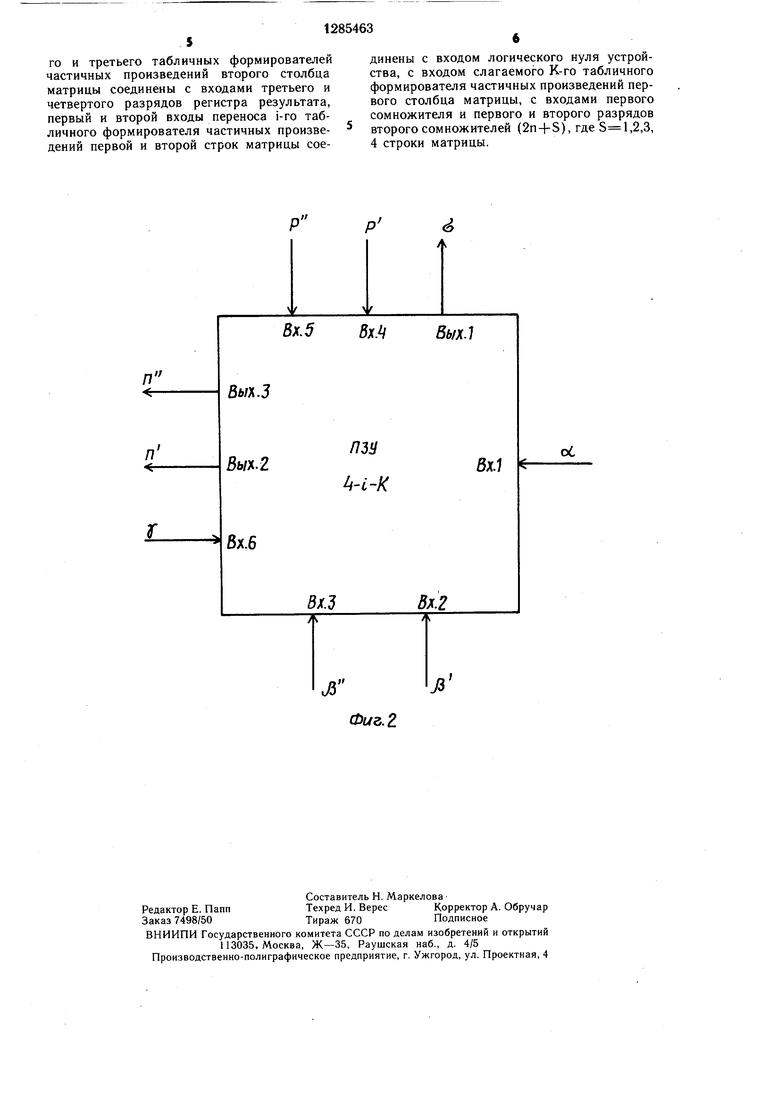
На фиг. 1 изображена функциональная схема устройства; на фиг. 2 - нумерация и обозначение входов и выходов табличного формирователя частичных произведений, выполненного в виде постоянного запоминающего устройствам (ПЗУ).
Устройство (фиг. 1) содержит 2п-раз10
Эта таблица замкнута в том смысле, что при любых двухразрядных кодах входного переноса Р по формуле (3) получается входной перенос П, имеюший не более, чем двухразрядный код. Таким образом, ПЗУ, реализующие данную таблицу истинности, могут быть включены в последовательную цепочку, где выход переноса П предыдущего ПЗУ подключен к входу переноса Р последующего ПЗУ.
Рассмотрим алгоритм умножения, реализуемый в устройстве.
Пусть комплексное число Ъ - множимое - представлено двоичным кодом
K(Zi) ак,...,ак,...До(5)
по основанию р л/2 , где j - 1, комплекс
рядный регистр 1 множимого, 2п-разрядный ное число Ъч - множитель - представле30
35
регистр 2 множителя, (4п+4)-разрядный регистр 3 результата и ( 4п) табличных формирователей частичных произведений, объединеных в матрицу. В нем каждый табличный формирователь 4 матрицы вы- 20 полнен в виде ПЗУ 4 с щестью адресными входами и тремя выходами. В каждом i-м столбце матрицы находится п ПЗУ 4, а в каждой j-й строке (2п + 4) ПЗУ 4.
Входы и выходы ПЗУ имеют следующие обозначения, -нумерацию и назначение 25 (фиг. 2): вход а первого сомножителя, вход 7 слагаемого, входы и р - первый и второй разряды второго сомножителя, первый и второй входы Р и Р переноса, выход а результата, первый и второй выходы П и П переноса.
На адресные входы ПЗУ поступает код, состоящий из разрядов
Квх (ее, Y, Р , Р, Р , Р). (1)
Этот код является адресом считывания. При его поступлении на входы ПЗУ на выходах этого ПЗУ появляется трехразрядный код, записанный в ПЗУ по данному адресу и содержащий разряды
Квь.х (а, П, П )(2)
Таблица истинности, связывающая коды KBX и в ПЗУ, реализует операцию умножения слагаемого а на число р, представленное двумя разрядами и с учетом входного переноса Р, представленного двумя разрядами Р и Р и слагаемого -у. При этом вырабатывается результат о и выходной перенос П, представленый двумя разрядами П иП . Формула этой операции имеет вид
6-2П 7+Р+а-р(3)
Вычисления по этой формуле выполняются в системе счисления по основанию (-2), т.е. числа П, Р, р представляются двухразрядными кодами по основанию (-2). В частности
(0)00,
(1)01,(4)
(-1) и, К-.(-2) 10
40
45
50
55
но двоичным кодом по основанию Р
К (Z2)pM ,...,p,....po.(6)
Произведение
Z Zi Z2(7)
будем искать в виде двоичного кода по ос- нованию-р
K(Z) afli,...,a,,...,0o .(8)
Триады множителя чередуются в следующем порядке:
р2 PI ро рз Р2 PI
Рб р5 4
Рт Рб PS
(9)
РШ Pm-l Pm-2, Pm+1 РШ Pm-l Рт-Ь4 Рт + З pm+2 Pm+5 Pitl+4 Pm4-3
Для каждой триады выполняется следующая последовательность действий: оп- ределя.ется код р К (Zi); определяется величина Sm-2 (О, 1,- 1, 2), зависящая от разрядов триады следующим образом:
1°
Sm-2 -, если (PmPm-lPm-2)
(10)
(Zl).
(11)
И определяется код
rn- l
РОт-2
Код произведения определяется по формуле
K(Z) ..,K(ZO(12)
где m. (2;+ 2) при i четном, (2/-4- 1) при i нечетном.(13)
Эта формула может быть записана в рекуррентном виде
K(Z,-) K(Z,,)+ (ZO, (14) где Z, - частичное произведение, причем K() 0.(15)
0
Эта таблица замкнута в том смысле, что при любых двухразрядных кодах входного переноса Р по формуле (3) получается входной перенос П, имеюший не более, чем двухразрядный код. Таким образом, ПЗУ, реализующие данную таблицу истинности, могут быть включены в последовательную цепочку, где выход переноса П предыдущего ПЗУ подключен к входу переноса Р последующего ПЗУ.
Рассмотрим алгоритм умножения, реализуемый в устройстве.
Пусть комплексное число Ъ - множимое - представлено двоичным кодом
K(Zi) ак,...,ак,...До(5)
по основанию р л/2 , где j - 1, комплекс ное число Ъч - множитель - представле
но двоичным кодом по основанию Р
К (Z2)pM ,...,p,....po.(6)
Произведение
Z Zi Z2(7)
будем искать в виде двоичного кода по ос- нованию-р
K(Z) afli,...,a,,...,0o .(8)
Триады множителя чередуются в следующем порядке:
р2 PI ро рз Р2 PI
Рб р5 4
Рт Рб PS
(9)
РШ Pm-l Pm-2, Pm+1 РШ Pm-l Рт-Ь4 Рт + З pm+2 Pm+5 Pitl+4 Pm4-3
Для каждой триады выполняется следующая последовательность действий: оп- ределя.ется код р К (Zi); определяется величина Sm-2 (О, 1,- 1, 2), зависящая от разрядов триады следующим образом:
1°
Sm-2 -, если (PmPm-lPm-2)
(10)
(Zl).
(11)
И определяется код
rn- l
РОт-2
Код произведения определяется по формуле
K(Z) ..,K(ZO(12)
где m. (2;+ 2) при i четном, (2/-4- 1) при i нечетном.(13)
Эта формула может быть записана в рекуррентном виде
K(Z,-) K(Z,,)+ (ZO, (14) где Z, - частичное произведение, причем K() 0.(15)
В этом алгоритме не возникает перенос из предыдущей триады множителя в последующую, имеющий место при умножении на два разряда двоичных кодов по основанию 2,
Устройство функционирует следующим образом.
Потенциалы с выходов регистров 1 и 2 сомножителей поступают на входы а, pi, Ра всех ПЗУ 4-J-i. Все входы ПЗУ 4-0-0 и 4-О-1 оказываются определенными (так как остальные входы этих ПЗУ присоединены к потенциалу «О и на их выходах образуются потенциалы, значения которых определяются формулой (3) при . Переносы П с выходов этих ПЗУ передаются на входы следующей пары ПЗУ 4-О-2 и 4-О-3 и т. д. Коммутация переносов такова, что реализуется алгоритм операции (3) при Y О с двоичными кодами комплексных чисел по основанию .
Таким образом, ,нулевая строка матрицы ПЗУ представляет собой сумматор, выполняющий операцию:
(Z,),(16)
где So определяется по (10) в зависимости от значений разрядов ро и Р2, т.е. состояния триггеров 2i и 2з регистра 2.
Код Ко изображается потенциалами на первых выходах ПЗУ 4-О-К и поступает на входы ПЗУ первого столбца матрицы, который организован аналогично предыдущей. Этот столбец выполняет операцию
Ki Ko+pSi K(Z,),(17)
где код К| изображается потенциалами на первых выходах ПЗУ , принадлежащего нулевому столбцу матрицы, и всех ПЗУ 4-1-4К, принадлежащих первому столбцу матрицы.
Аналогично второй столбец матрицы выполняет операцию
K2 Ki+p S4K (Z,),(18)
где код К2 изображается потенциалами на первых выходах ПЗУ 4-О-О, прцнадлежа- щего нулевому столбцу матрицы, ПЗУ 4-1-О, 4-1 - 1, 4-1-2, принадлежащими первому столбцу матрицы и всех ПЗУ 4-2-К, принадлежащих второму столбцу матрицы. Третий столбец матрицы выполняет операцию
K3 K2P S5K(Z,)(19)
и т. д. В общем случае i-й столбец матрицы выполняет операцию
K, K/-i+p - S 2K(Zi),(20)
где ш определяются по (13).
Сравнивая формулы (14) и (20) замечаем, что код К/ является кодом К (Z/), т.е. кодом частичного произведения Z/.
Наконец, последний (п-1)-й столбец матрицы вычисляет код произведения: К (Z),
0
5
0
5
0
5
0
5
0
5
который изображается потенциалами на первых выходах ПЗУ.
Эти выходы подключены к входам установки регистра 3 результата. Таким образом, разряды регистра произведения устанавливаются сигналами на первых выходах перечисленных П32 4-i-К.
При выполнении операции (20) перенос может распространяться на четыре разряда влево, поэтому в каждом столбце матрицы должно быть (2п-|-4) ПЗУ 4. Количество столбцов в матрице равно п (а не 2п) за счет того, что в каждом столбце матрицы реализуется умножение на два разряда множителя.
Формула изобретения
Устройство для умножения, содержащее регистры множимого, множителя и результата, отличающееся тем, что, с целью расширения класса решаемых задач за счет обеспечения возможности умножения комплексных чисел, в него введена матрица п(2п+4) табличных формирователей частичных произведений, (где 2п - разрядности множимого и множителя), причем вход первого сомножителя j-ro табличного формирователя частичных произведений (где j 1,2,...,2п) i-ro столбца (где i 1,2,...,п) соединен с выходом j-ro разряда регистра множимого, выходы К-го и (К-Ь2)-го разрядов регистра множителя (где при i четном, 2i-1 при i нечетно.м) соединены соответственно с входами первого и второго разрядов второго сомножителя i-ro табличного формирователя частичных произведений j-и строки матрицы, первый и второй выходы переноса 1-го табличного формирователя частичных произведения К-й (где К 1, 2,...,2п-|-4) строки матрицы соединены соответственно с первым и вторым входами переноса (К+2)-го табличного формирователя частичных произведений i-ro столбца матрицы, вход слагаемого ()-ro табличного формирователя частичных произведений (-|-1)-го столбца матрицы соединен с выходом результата -го табличного формирователя частичных произведений (где В J + 1 если i нечетно, --ЬЗ если i четно) 1-го столба матрицы, выход результата (i-|-2)-ro табличного формирователя частичных произведений первой строки (при i нечетном) матрицы соединен с входом (2i-1)-го разряда регистра результата, выходы результата (i+2)-ro табличного формирователя частичных произведений (при i четном), т-й строки (т 1,2,3) матрицы соединен с входом ()-го разряда регистра результата, выходы результата первого и второго табличных формирователей частичных произведений первой строки матрицы соединены соответственно с входами первого и второго разрядов регистра результата, выходы результата второго и третьего табличных формирователей частичных произведений второго столбца матрицы соединены с входами третьего и четвертого разрядов регистра результата, первый и второй входы переноса i-ro табличного формирователя частичных произведений первой и второй строк матрицы соеР Р
у ъ
5x5
Вш.5
5ь/х.2
-L-K
Вх.З
динены с входом логического нуля устройства, с входом слагаемого К-го табличного формирователя частичных произведений первого столбца матрицы, с входами первого сомножителя и первого и второго разрядов второго сомножителей (2n + S), где ,2,3, 4 строки матрицы.
5хЛ
бб/л.1
ВхЛ
об
В}(.2
Фи&.2

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения чисел | 1990 |
|
SU1714595A1 |
| Устройство для умножения | 1989 |
|
SU1654815A1 |
| Скалярный умножитель векторов | 1988 |
|
SU1619254A1 |
| Устройство для умножения @ - разрядных чисел | 1989 |
|
SU1735843A1 |
| Устройство для умножения | 1990 |
|
SU1753471A1 |
| Устройство для умножения в избыточной четверичной системе счисления | 1983 |
|
SU1160399A1 |
| Устройство для умножения с накоплением | 1982 |
|
SU1108087A1 |
| Устройство для умножения | 1980 |
|
SU1005039A1 |
| Устройство для умножения двух @ -разрядных чисел | 1988 |
|
SU1575174A1 |
| Устройство для умножения | 1989 |
|
SU1658148A1 |
Изобретение относится к области вычислительной техники и может быть использовано в составе цифровых вычислительных машин, предназначенных для решения задач с комплексными числами в области электроэнергетики, связи, гидродинамики. Целью изобретения является расширение класса решаемых задач за счет обеспечения возможности умножения комплексных чисел. Устройство представляет собой матричное множительное устройство, в котором каждый столбец табличных формирователей частичных произведений 4 выполняет умножение содержимого регистра 1 множимого на два разряда регистра 2 множителя и сложение этого произведения с результатом, образованным в предыдуш,ем столбце. Переносы в столбце распространяются по правилам алгебраического сложения комплексных чисел. 2 ил. fi (Л N5 00 ел 4 О5 оо


| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ОПЕРАЦИЙ С КОМПЛЕКСНЫМИ ЧИСЛАМИ | 0 |
|
SU377769A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Карцев М | |||
| А | |||
| Арифметика цифровых машин.-М.: Наука, 1969, с | |||
| Способ образования окрасок на волокнах | 1925 |
|
SU437A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
Авторы
Даты
1987-01-23—Публикация
1985-09-02—Подача