Изобретение относится к машиностроению, в частности к станкостроению, и может быть использовано для шлифования наружных и внутренних поверхностей тел вращения.
Цель изобретения - повышение точности формы шлифуемой поверхности вращения, производительности шлифования.
На чертеже изображена схема контактирования профиля детали с плоскими опорами.
При исследовании движения детали, базирующейся на опорах, использован ряд допущений: номинальная поверхность базы детали является поверхностью вращения; упругая податливость материалов детали и опор не учитывается; поверхность опор не
имеет отклонений Формы; внешний реальный профиль Г сечения детали (фиг.1) контактирует с каждой из двух поверхностей опор лишь в одной точке, что возможно, если профиль является выпуклым и мала ширина зоны контакта детали с опорами. Тем самым ниже не рассматриваются случаи моногармони- ческого профиля с высшими гармониками отклонения формы; угол Д реального профиля Г в плоскости А сечения детали считается заданной функцией времени t, A A(t).
Пусть f S(if) - R + fl(lf), (1) - уравнение кривой профиля Г в рассматриваемой плоскости Л в полярной системе координат с началом в точке С - центре средней окружности профиля, радиус которой R, и баСП
Ј
1C ГС
зисным лучом СР, жестко связаннымгде п
лучом СР, жестко связанным с профилем Г. Представим функцию з(чО рядом Фурье на промежутке 1Г и ограничимся рассмотрением лишь тех случаев моногармонического профиля, гармоники отклонения формы которого не нарушают выполнения односвязностиЈ
области контактирования профиля Г детали с плоскостями опор П1э Пг
N
(2)
h V/ 0, jeh- номер, ампли и начальная n-й гармоник клонения от ло сти. Введем обозначения лт тах|
10
дт
Т
An . L (ц
dm 6W йт
MY) Т A Sin(nif + ж„),
п«2
9h nif + zn , тогда уравнение (2) примет вид
f R(1 + Ј% ahsin0J R U + Јu(if). (3)
ml
п
h V/ 0, jeh- номер, амплитуда и начальная фаза n-й гармоники отклонения от кругло сти. Введем обозначения лт тах|л(ч)|;
Ј
дт
Т
An . L (ц
dm 6W йт
9h nif + zn , тогда уравнение (2) примет вид





| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ЧИСТОВОЙ И УПРОЧНЯЮЩЕЙ ОБРАБОТКИ ПОВЕРХНОСТЕЙ ТЕЛ ВРАЩЕНИЯ СЛОЖНОГО ПРОФИЛЯ | 2010 |
|
RU2493954C2 |
| Способ точения некруглых в попереч-HOM СЕчЕНии ТЕл | 1977 |
|
SU818752A1 |
| СПОСОБ БЕСЦЕНТРОВОЙ ОБРАБОТКИ КРУПНОГАБАРИТНЫХ ДЕТАЛЕЙ ТИПА КОЛЕЦ | 1991 |
|
RU2040375C1 |
| Способ обработки отверстий с наклонной образующей | 1990 |
|
SU1803278A1 |
| Способ суперфиниширования валов | 1990 |
|
SU1824289A1 |
| Способ шлифования желоба на круглой детали | 1989 |
|
SU1731601A2 |
| Способ чистовой обработки детали | 1989 |
|
SU1703417A1 |
| Стенд для градуировки и определения жесткости ротационных динамометров и тензометрических валов | 1989 |
|
SU1749737A2 |
| СПОСОБ РАЗНОСТНОГО ИЗМЕРЕНИЯ ОТКЛОНЕНИЯ ОТ КРУГЛОСТИ | 2002 |
|
RU2239785C2 |
| Виброизмерительный преобразователь | 1989 |
|
SU1641457A1 |

Изобретение относится к машиностроению, в частности к точному станкостроению, и может быть использовано для шлифования бесцентровым способом наружных и внутренних поверхностей вращения жестких тел. Цель изобретения - повышение точности формы шлифуемой поверхности вращения и производительности шлифования за счет оптимизации величины угла разведения неподвижных плоских жестких опор и направления воздействия режущего инструмента - шлифовального круга на обрабатываемую деталь в соответствии с минимальным смещением геометрического центра детали при ее движении в опорах, обусловленным доминирующей гармоникой профиля базы. При этом половинный угол разведения опор при воздействии инструмента на деталь вдоль оси симметрии опор определяется из математического выражения. 1 ил, 1 табл.
Для высокоточных деталей (например, колец подшипников, валов, втулок) Ј имеет порядок , поэтому ограничимся результатами асимптотических разложений по степеням Ј в первом приближении.
Рассмотрим случай, когда опоры являются плоскостями (фиг. 1). Введем неподвижную систему координат OXY (фиг. 1), с началом в центре вспомогательной окружности радиуса R, соприкасающейся с плоскостями опор nf и ГЦ. Ось X направим по биссектрисе угла разведения 2 -у плоскостей П, и П4. В этой системе координат положение точки С - центра средней окружности реального профиля детали, контактирующего с плоскостями П1 и П2 в точках К, и К.задается координа- тами Хс; Yc; Е -JX. + Тгс: ОС, где величина Е характеризует смещение точки С от расчетного положения О
Уравнения прямых Р
получен11 L г ных в результате сечения плоскостей
ОПОР П1 И П2 ПЛОСКОСТЬЮ А, ОПИСЫВаЮТ-
ся следующими уравнениями, соответственно для первой и второй прямой, составленными для случая, когда прямая проходит через точку с известными координатами т. А(ХД, О) и извест- ным направлением
1
Ґл + (Х1 - XA)tgr;
как
YJ YA - (Ха - X/Otgf, так
Y, 0, то
Y, (X1-XA)tgr; Y2-(X -XjHgy
(Х1( Y,); (X.,, Y.J) - коордшсаты
точек касания К 1 и 1Ц профиля с прямыми Р, и Р7. Если учесть,
Ј i у ;
X;sin у R, то уравнения в общем виде для прямых P{(i 1 2) имеют вид
Y; S;(X;tgr- Rsec -у ) ;
1; при i 1
где S-
(5)
-1; при i
Предполагая известным уравнение (1) профиля Г детали и угол разведения плоскостей опор 2-v, рассчитаем траекторию движения точки С при изменении угловой ориентации профиля детали, задаваемой углом А A(t) между осью ОХ и базисным лучом полярной системы координат СР.
Составим уравнения, отражающие геометрические условия контактирования профиля Г детали с плоскостями П, и П2.
Первое условие - условие равенства координат точек касания кривой профиля Г с прямыми Pt; (i 1, 2)
Для точки касания
К., : Хл Ecos «jt + p(if,)-cos(if,+;0;
Y Esin o(+ f( 4,)sin(, + Л ) , (6)
Для точки касания К /j
Х Ecos oi+ f ( V,)cos(if4+ A);
Y Esin Ы+ j (if4)sin( iff A). (7) С учетом того, что Ecosd Xc;
Yc, уравнения в общем виде
будут следующими
Xi Хс + р (cos(+ A);
Yt - ()sin(A);(8)
Второе условие - условие коллинеарности касательных к кривой профиля
Г И ПрЯМОЙ Р; В
точке касания К
Piff о
vT.
, + Р-Ро
5о
Для точки К,х X/R; у Y/R; х, Xj/R;
у, Ј6(.) Ј(Ч,-) Ј{
ffrcoB(«/.+ ./) - psinC -M) (g)глов f-.; 4(1-1,2);
V(r-i/) + ft
ift+ Л - -S,- /з- /,-. Для точки КгУгол j. характеризует отклонв7
ние нормали к кривой профиля в точке
р цсо8( t/gf А ) - Ј sin(t/fr+ р ) Kj от радиального направления полярj( , ч22 ной системы координат, связанной с
деталью.
Уравнения (5-9) представляют собойОчевидно, что при малых Ј , велисистему восьми трансцендентных алгеб- чины X.,; Yt; J, ; с являются малыми раических уравнений относительно вось- величинами порядка Ј. Исключение не ми неизвестных: X; Y; X,; Y1; Xf; известных X,; Х4; vt; Y производим Ј, V.« С целью упрощения записи после- подстановкой уравнений (8) и (3) в дующего решения этой системы введемуравнения (5) и (9).
обозначения безразмерных координатДля точки К :
i20 |
р Esino(+ R(1 +E1)sin(ifi+A) Ecosd R(1 +Ј,)Cos (Jt+ A) tg 7- -Ј-; ;
(10)
сКе ,со8(1/,+ А ) - R(1 +Ј,)в1п(/1+Л ) cosj.R -V(1 + + (ЈV,)S . Для точки К ч
I
Esin e{+ R(1 + Ј2)81п(+ Д ) - Ecoso + R(1 +e4)cos(+ A)-tg|+ ; ,
RE2COs(t+ ) - R(1 +Јpsin() -cos|-R --/(1 +)2 + (E %)2 . (11)
Пренебрегая малыми величинами вто- обозначенияfуравнения (10) и
рого порядка и приняв во внимание(11) примут вид
ус + (1 +E,)ein((f1+A) xc - U +Ei)cos(+A)
I
(1,+ / ) - (1 +Ј,)ein(if+) (1 +е,)(12)
Ус + (1 +Ei)sin(ift+) + (1 +Ei)cos(yt+ )tgy+ - ; E cosdf A ) - (1 +Ј2)з1п(+Л) -(1 +Јz)cos7 .(13)
Из чертежа следует, чтоПодставив уравнение (14) в уравне. ония (12), (13), заменив синус и ко11 ....ч 45 синус суммы двух на сумму синусов
л - X1и КОСИНУСОВ и пренебрегая произведе II нием малых величин, получим следующие
уравнения
ус -сЛ, cos/з - sin/i- Ј1sin,xc + cosp + Ј,cospd,sin/i - tg J
. rfi - - ЈVt,
;Ус + sinp+ sin/ь xc + cos/ь + Jl4sinp tg|-+ - ;
A--E .)
(15)
Сложим уравнения (15) и (16) и вычтем из первого второе, приняв во
2ус + (E-a-Ј,)sinp + (& фсовр (Ј,- 64) cos p + (E ,-+Ei)sinp ctg /i ;
ем
X,-2sin/i+ (E rEpcosp- (Ј1 + Ј2)sinp 2xc + 2cosp- + (Ј, Ј2)
(17)
Упростив уравнение (17), получа-Уравнения (18) задают движение
точки С в безразмерных декартовых - Ј. - с Ь( Ч|) + & (Чг). (ig) координатах, а значит и движение
А -. - . St1ял 4 Д
сечения детали, которому принадлежит 1S точка С, являясь его центром.
2cos/3 Јi-Ј P6(tfi) -Ь (Ч).
-- С
Ус Zs in p2sinp
Проанализируем геометрические характеристики траектории движения точки С. Введем безразмерный параметр е , характеризующий расстояние между точками С и О
20
Проанализируем геометрические характеристики траектории движения точки С. Введем безразмерный параметр е , характеризующий расстояние между точками С и О
, Л - БЧ,- -Ј6 (if,);
J-1 E t, - Ј6 (i/4).
Е 1 ,ПГ 1 Г 1±М2+ (2 - 1 Jpi+P2 - 7F f r-ns A(19)
е - - V х + v - I -я-+ ;-; - -гт V t + Ь t-4cos P
дп ЈЈV ncos2/5nsin2 Јsinz/34г
Из формулы (19) для профиля (2) A(f) Ahsin(ntf) или Ь ()
при наличии одной гармоники отклоне- a sintn); i 1,2.
С учетом уравнений (14) и (2) и (19) после тригонометрических преобразований следует, что
е /siti pcos2 (np)sin2 fnA(t)J + cos2p-sin2 (np) cos2- n A(t)J . (20)
ния формы (многогармонический профиль) с номером п 7 1
sin2j
V
Величина е принимает экстремаль1Гт
ные значения при А х-
/п
где т - натуральное число, если tg р t Jtgnp V.
В случае tp, p jtgn/з) (21) - величина е постоянна и равна е
Для моногармонического профиля уравнение (18) имеет следующий вид cos(nfi)sin(nA).
„.„.. (22)
Ус А1
х - А с n cos р
sin(n/s) cos (nA)
smp
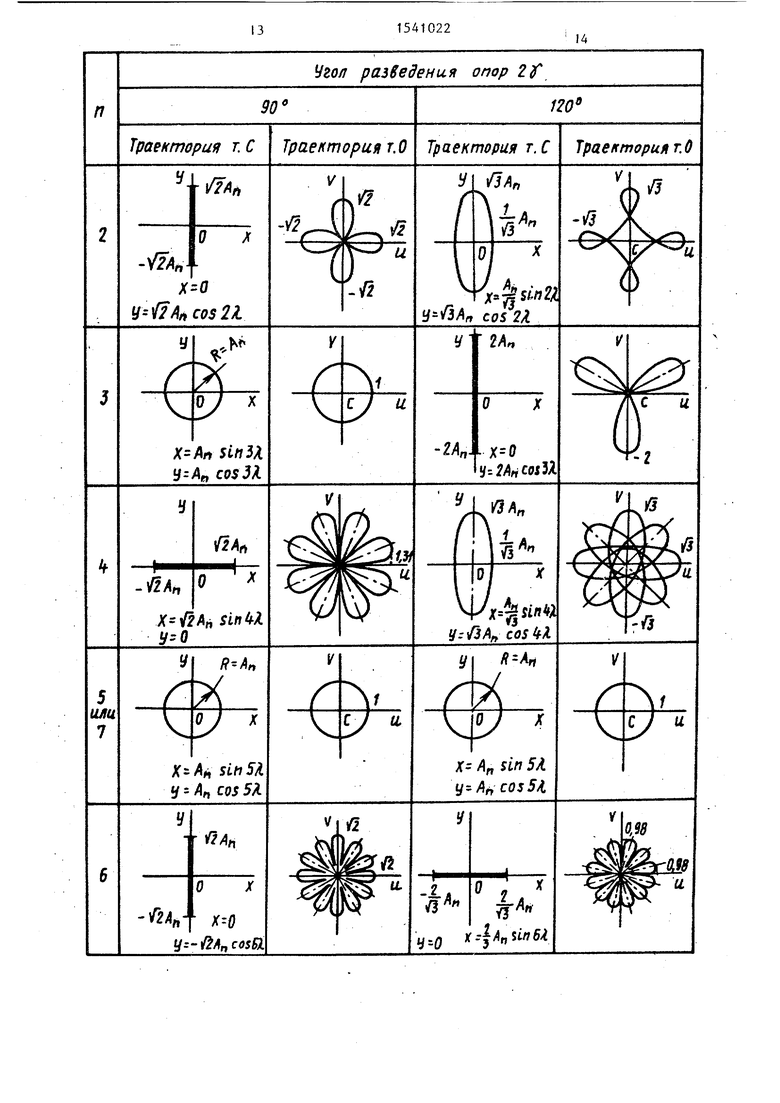
Система уравнений (18), (20) для различных сочетаний п и у позволяет получить траекторию движения точки С относительно неподвижной системы координат OXY, связанной с опорами, и траекторию движения точки О относительно подвижной системы координат Cuv, связанной с профилем Г сечения детали. На таблице представлены указанные траектории точки 0 и точки С для некоторых значений пи -у .
внимание, что tp, y ctg p; cos -у - - sin р и подставив значения cf получим
Проанализируем геометрические характеристики траектории движения точки С. Введем безразмерный параметр е , характеризующий расстояние между точками С и О
Полученные аналитические зависимости (18, 20) позволяют рассчитать теоретическое положение детали при ее движении в любой момент времени и определить отклонение найденного положения от номинального. Другими
словами, стало возможно рассчитать теоретическую точность конкретного (Движения детали, имеющей конкретный моногармонический профиль базы, при базировании на плоских неподвижных
жестких опорах. Кроме того, на основании траектории движения точки С определяется направление, вдоль которого перемещение сечения, а вместе с ним и детали, будет наименьшим,
а с помощью системы уравнений (18) рассчитывается величина этого перемещения для фиксированных значений п и у.
Например, для п 2, 2-у 120° и амплитуды А наименьшее перемещение детали происходит вдоль координатной оси ОХ (см.табл.), а величина этого перемещения равна Ап-2//3,
2-v
9 90°
15
для n 4, } u перемещение вдоль координатной оси OY оказалось равным нулю.
На основании полученных результатов (см.табл.) можно утверждать, что при известной форме базовой поверхности, т.е. известных номерах n доминирующих гармоник отклонения ее профиля, можно однозначно определить такой угол разведения опор 2 и такое направление действия инструмента на деталь (причем, направление будет либо по оси симметрии опор, либо вдоль прямой, перпендикулярной оси симметрии опор и проходящей через центр т.О фиг. 1 детали), что исходная погрешность профиля базовой поверхности не передается на обрабатываемую. Из данных таблицы выводится формула половинного угла разведения опор: а) при направлении действия инструмента на деталь вдоль оси симметрии onop-v 90° - где k - натуральное
180
2k 1 2п
град, (23)
число, удовлетворяющее условию -j 2k + 1 - (24)
б) при направлении действия инструмента на деталь вдоль прямой, перпендикулярной оси симметрии опор и проходящей через центр детали т.О у
90
о
180°п
град,
(25)
где k - натуральное число, удовлетво(26)
ряющее условию 2k i .
Предложенный способ бесцентрового шлифования реализуется следующим образом. Берется деталь типа тела вращения (вал, кольцо, втулка) с известным измеренным реальным профилем базовой поверхности в месте контакта детали с опорами, что позволяет определить доминирующую гармонику n базы. По известной доминирующей гармонике n выбирается направление воз действия режущего инструмента - шлифовального круга на обрабатываемую деталь либо вдоль оси симметрии плоскостей опор, либо в направлении, пер 36000 об/мин; t 1500 мм/мин; марка круга 24А10С1К5 ПП 3 чены следующие резул 50 Пример 1. n отклонение от кругло направление действия на деталь - вдоль ос отклонение от кругло
пендикулярном оси симметрии опор вдоль линии, проходящей через геомет- 55 поверхности 0,2 мкм. рический центр детали, так как именно вдоль указанных направлений, определенных в результате теоретико- экспериментальных исследований, смеПример 2. n отклонение от кругло направления действия
1541022
10
щение геометрического центра детали при ее движении в опорах минимально и обусловлено доминирующей гармоникой (табл.), а стало быть при формировании нового профиля не передадутся погрешности базы на обрабатываемую поверхность. Правильность выбора направления воздействия инструмента 0 на деталь определяет справедливость неравенств (24, 26), связывающих коэффициент k и номер доминирующей гармоники п. В соответствии с выбранным направлением определяется поло- 5 винный угол разведения опор либо по формуле (23) при направлении действия инструмента на деталь по оси симметрии плоскостей опор, либо по формуле (25) при направлении воздействия ин- 0 струмента на деталь вдоль линии, проходящей через геометрический центр детали перпендикулярно оси симметрии плоскостей опор. Далее разводят опоры на величину найденного угла и уста- 5 навливают направление воздействия .инструмента на деталь, выбранное ранее. Затем деталь устанавливают в опоры и жестко фиксируют в осевом, упруго фиксируют в радиальном направ- 0 лениях, например, с помощью магнитного патрона. Производят обработку требуемой наружной или внутренней поверхности детали.
Предложенный способ повышает производительность обработки за счет быстрого достижения точности формы обрабатываемой поверхности, что не требует дополнительных технологических операций.
0 При обработке центрового отверстия диаметром 5 мм в высокоточной детали типа вала из стали ШХ15, HRC 52...55 на специальном внутргаштнфо- вальном станке 3225П при режимах 5 пдет 100° об/мин; n шл. кр
36000 об/мин; t 0,1 мм; Sпр 1500 мм/мин; марка шлифовального круга 24А10С1К5 ПП 3x6x1 были получены следующие результаты. Пример 1. n 2, 2Ц - 90% отклонение от круглости базы 0,9 мкм, направление действия инструмента на деталь - вдоль оси симметрии опор, отклонение от круглости обработанной
5
5 поверхности 0,2 мкм.
оверхности 0,2 мкм.
Пример 2. n 3, 2f 120°, отклонение от круглости базы 1,1 мкм направления действия инструмента на
деталь вдоль оси симметрии опор, отклонение от круглости обработанной поверхности 0,3 мкм.
Пример 3. п « 3, 2 у- 90, отклонение от круглости базы 1,1 мкм направление действия инструмента на деталь - вдоль прямой, перпендикулярной оси симметрии опор и проходящей через центр детали. Отклонение от круглости обработанной поверхности 2,4 мкм.
Предлагаемый способ обеспечивает повышение точности формы шлифуемой поверхности и производительности обработки.
Формула изобретения
Способ бесцентрового шлифования тел вращения, включающий развадение угла неподвижных плоских жестких опор, жесткую фиксацию в опорах в осевом направлении и упругую фиксацию в радиальном направлении детали с известным профилем базовой поверхности и определенной в нем доминирующей гармоники, воздействие инструмента на деталь, отличаю щи й с я тем, что, с целью обеспечения повышения точности формы шлифуемой поверхности и производительности шлифования, выбирают направление воздей
5
ствия инструмента на деталь либо вдоль оси симметрии плоскостей опор, либо в направлении, перпендикулярном оси симметрии плоскостей опор вдоль линии, проходящей через геометрический центр детали, в соответствии с минимальным смещением геометрического центра детали при ее движении в опорах, обусловленным доминирующей гармоникой, при этом половинный угол f разведения опор при воздействии инструмента на деталь вдоль оси симметрии опор определяется из соотношения
Г 90 - 180 2k±+n 1 , град.
и при воздействии инструмента на деталь в направлении, перпендикулярном оси симметрии плоскостей опор вдоль линии, проходящей через геометрический центр детали, определяется из соотношения:
у- 90 - 180 k/n, град,,
где п - номер доминирующей гармоники отклонения профиля базовой поверхности; k - коэффициент, зависящий от
разновидности отклонения про- еЬиля базовой поверхности.
Уго/r разведения опор 2f
П
90
Траектория т. С
Траектория т.О
г
-Я
-V2An
V tfA cos2l
5МЗД С05Л
UA,
-U К
SinbX.
R--A,
5
или
7
slftSt. у - An cos 5Я
UA
V|V2
-fiA X--0
y -&AncosKL
120(
Траектория т. С
Траектория т.О
и
jffasint У-ftAr, cos 2Я
2А,
U
2Ап..
У .2А„ш1.
и
x$5sM
У:&Ап COSM
LL
U
X А„ sin 5/i y-An cos 54,
и
i4я-л
Ц-0
KifaM
| Альперович Т.А | |||
| Теория копирования погрешностей базовой поверхности при внутреннем бесцентровом шлифовании | |||
| - Станки и инструмент, 1966, № 5, с | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
Авторы
Даты
1990-02-07—Публикация
1988-04-25—Подача