Изобретение относится к вычислительной технике и может быть использовано для умножения многоразрядных чисел в двоичных системах счисления.
Цель изобретения - расширение функциональных возможностей устройства за счет умножения в избыточных системах счисления.
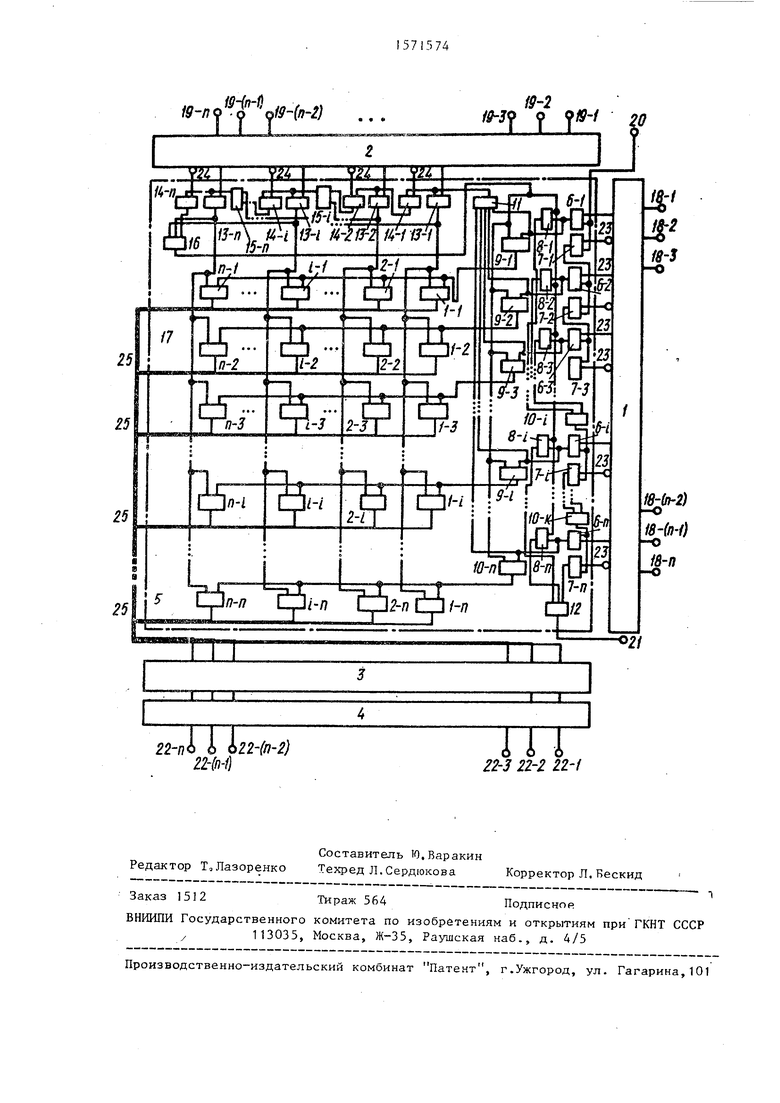
На чертеже приведена схема устройства для умножения многоразрядных чисел в двоичных избыточных системах счисления.
Устройство содержит регистр 1 множителя, регистр 7. множимого,шифратор 3, накапливающий сумматор 4, матрицу 5 элементов И из п столбцов и п строк , матрица 5 содержит элементы И 6-1, 6-2,..., 6-г,.,., 6-п,
элементы И 7-1, 7-2 7-i,..0,7-n,
элементы И 8-1,8-2,...,8-i,...,8-nt триггеры 9-1, 9-2, ..., 9-i, ...,9-n, элементы ИЛИ 10-i,..., 10-n, элементы ИЛИ 11 и 12, элементы И 13-1, 13-2, ..., 13-i, ..,, , элементы И 14-1, 14-2, ..., 14-1, ...,14-п, элементы ИЛИ 15-j, ..,, 15-п, элемент ИЛИ 16, элементы И 17-1-1, 17-1-2, .... 17-п-п.
сл J
ел i
Входы 18-1, 18-2, ..., iR-n являются информационными входами регистра 1 ,входы 19-1 ,19-2,..., 19-п-входами регистра 2,вход 20 - управляющим входом устройства, выход 21 - выходом окончания умножения, выходы 22-1,
22-2,
... ,
22-п - выходами накапливающего сумматора 4, выходами кода произведения.
Любое число в двоичных избыточных системах счисления (в традиционной классической системе счисления такж,е) может быть представлено как
А
ъДО,
(О
где a-e(o,l, причем а; 1
при выполнении условия п
L.(i) 6 A-21a;Lg(i) iLe(i + 1), i-«(2)
причем
О, при i 0;
(3)
Б, при Об1б 1;
е+л
21 Lp(i-l-j), при .
Н E
В формулах (О, (2), (3) под i принимается номер разряда (i О, 1, 2,,,о, N), под Г - номер системы счисления (1 0, 1,2,..,,N),D- произвольное число, могущее принимат значения в интервале целых чисел от -N до +N, но в конкретном случае от 0 до N, А и В - целые произвопь- ные числа, равны О, I,2,..,НвА$3$3, но могут быть системы, когда общее неравенство принимает вид равенства, Lp(i) - имя системы счисления, однако на практике оно значительно меньше, J определено в формуле (3), Выражение (2) задает форму представления чисел.
Условие (.) справедливо для минимальной формы изображений9 предполагающей наличие минимального количества единиц в изображении числа, а также характерной строго обозначенным снизу количеством нулей между единицами К. Для минимального изображения в р-системах счисления Фибоначчи К р (4), для двоичной ,1-системы
видно, что при уменьшении основания системы счисления возникает возможность производить построение форм изображения чисел по определенному алгоритму, в нашем случае его задает выражение (2) для систем счисления (3) и использовать эти особенности для увеличения быстродействия при выполнении арифметических операций.
Реализованный способ умножения основан на принципе таблицы умножения и состоит в следующем.
1.В столбец записываются в порядке возрастания веса конкретно выбранной системы счисления.
2.В строку записываются в порядке возрастания веса конкретно (той же, что и для столбца) выбранной системы счисления.
3« На пересечении строк и столбцов записываются произведения весов соответствующих строк нз веса соответствующих столбцов, причем в соответствии с выражением
0
5
тт/
Lf(i)
0, при ,
Lg(m), при 1, (4)
ЕЛА
5lL8(i-l-j), при ,
J-B где i - номер столбца;
m - номер строки;
i - номер разряда множимого,
m - номер разряда множителя.
4.Произведения, попавшие на пересечение строк и столбцов в аналогичных разрядах сомножителей, имеющих коэффициент а; 1, являются частными произведениями.
5,Просуммировав частные произведения, получаем окончательное, интересующее нас произведение сомножителей.
Рассмотрим приведенный способ умножения для двоичной 1-системы счис51571574
Выше iI 122345790,. - веса двоичной I-системы счисления, вычисленные в соответствии с выражением
в
О, при i -с 0, 1 , при , (5) V,(i-2) + Ц),(1 -3), при i 1.
Произведение веса i столбца на вес m-й строки определится, как
0, при i ± О,
Y(i) ) V,(ra), при , (6) V,(i-2) + V, (i-3), при i 1 . Рассмотрим умножение чисел 11 и 




| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для умножения п-разряд-НыХ чиСЕл | 1978 |
|
SU813417A1 |
| Устройство для умножения | 1978 |
|
SU888109A1 |
| Устройство для умножения | 1985 |
|
SU1285463A1 |
| Устройство для вычисления сумм произведений | 1973 |
|
SU480077A1 |
| Устройство для умножения | 1989 |
|
SU1612295A1 |
| Устройство для умножения чисел с контролем | 1988 |
|
SU1621033A1 |
| Вычислительное устройство | 1980 |
|
SU957203A1 |
| Устройство для умножения | 1988 |
|
SU1578711A1 |
| Матричное устройство для умножения двоичных и десятичных чисел | 1983 |
|
SU1200282A1 |
| Преобразователь позиционного кода в код с большим основанием | 1987 |
|
SU1444959A1 |
Изобретение относится к вычислительной технике и может быть использовано для умножения многоразрядных чисел в двоичных системах счисления. Цель изобретения - расширение функциональных возможностей устройства за счет умножения в избыточных системах счисления. Поставленная цель достигается тем, что в устройство, содержащее регистр множителя, регистр множимого, матрицу элементов И из N столбцов и N строк /N - разрядность операндов устройства умножения/, введены шифратор, накапливающий сумматор, в матрицу элементов И введены 5N элементов И, /2K+3/ элементов ИЛИ/K - МИНИМАЛЬНОЕ КОЛИЧЕСТВО НУЛЕВЫХ РАЗРЯДОВ МЕЖДУ БЛИЖАЙШИМИ СОСЕДНИМИ ЕДИНИЧНЫМИ РАЗРЯДАМИ В ПРЕДСТАВЛЕНИИ ЧИСЕЛ В ИЗБЫТОЧНЫХ СИСТЕМАХ СЧИСЛЕНИЯ/, N СЧЕТНЫХ ТРИГГЕРОВ С СООТВЕТСТВУЮЩИМИ СВЯЗЯМИ. 1 ИЛ.
В кружочки обведены частные произведения, которые необходимо просуммировать: 11x8 63 +14 + 9 + 2 88.
В данном случае i, m - веса разрядов множимого и множителя, над весами размещены кодовые записи чисел. В кружочках частные произведения чисел 4 на 2, 4 на 8, 8 на 2, 8 на 8. Имеем 10 х 12 8 + 16+32 + 64 120, т.е. произведения соответствуют истине. i
Устройство позволяет умножать числа, где множимое и множитель представлены в различных системах счисления, а произведение получено в третьей системе, отличной от системы i счисления и множителя и множимого. Это возможно благодаря введению в устройство шифратора, который может
Аналогично рассмотренному примеру происходит умножение в других системах счисления.
Рассмотрим пример умножения чиоел 12 и 10 в традиционной двоичной системе счисления:
быть построен в соответствии с выражениями (l) и (2) для любого слу- чая. Матрица частных произведений тогда будет определяться выражением
(4),
однако значение
L.(m)
при
О Ј i Ј. 1 будет определено весом системы счисления множимого.
Рассмотрим пример умножения чисел 6 и 18 в 2- и 3-системе счисления Фибоначчи.
В этом случае выражение (4) преобразится в следующее:
w 0 , при i ; 0,
/2ij(O V2(m), при ,(7)
j 0
if,(i-P-j), при i 3.
В данном случае i - веса 3-систе- мы счисления Фибоначчи, m - веса 2- системы счисления Еябоначчи, в кру- жочках частные произведения: 6 х х 18 84 + 24 108.
Устройство работ.ает следующим образом.
В регистр 1 записывается код мно жителя, в регистр 2 - код множимого, На вход 20 подается сигнал управления, который поступает на вторые входы элементов И 6-1, 7-1. Положим разряд регистра, к которому подключены элементы И 6-1, 7-1 нулевой, зто приведет к единичному уровню на первом входе элемента И 7-1, на выходе которого появится единичный сигнал, который передается на вторые входы элементов И 6-2, 7-2. Положим, что разряд, к которому подключены элементы И 6-2, 7-2 единичный, в этом случае первый вход элемента И 6-2 будет подключен к единичному сигналу, на его выходе появится единичный уровень, который установит триггер в единичное состояние, что в свою очередь приведет к тому, что на первых выходах элементов И 17-1-2, 17-2-2,..., 17-J-2, ..., 17-П-2 появится единичный сигнала единичный
сигнал через элемент ИЛИ 11 поступит также на вторые входы элементов И 13-1, 14-1. Положим, что опрашиваемый разряд регистра 2 (а именно к опросу его мы приступили), к которому прикреплены элементы И 13-1,14-1, равен нулю, тогда на выходе элемента И 14-1 появится единичный сигнал, так как на его входе два единичных сигнала с выхода элемента ИЛИ .11 и с инверсного выхода опрашиваемого раз0
5
0
5
0
5
5
ряда регистра 2, это приведет к тому, что на вторых входах элементов И 13-2, 14-2 появится единичный сигнал,, Положим, что регистр 2 имеет в разряде, к которому подключены И 13-1, 14-2 логическую единицу,тогда на выходе элемента И 13-2 появится единичный сигнал, .который передается на вторые входы элементов И 17-2-1, 17-2-2, 17-2-3, ..., 17-2-j, ... 17-2-п. На выходе элемента И 17-2-2 появится единичный уровень, так как на его входах единичный сигнал, выходной сигнал с элемента И 17-2-2 поступит через произведения матрицы 5 на соответствующий в силу выражений (l), (2) вход шифратора 3, где преобразуется в позиционный код интересующей нас системы и поступит на входы накапливающего сумматора 4 суммирующего числа в системе счисления шифратора. Одновременно единичный сигнал с выхода элемента И 13-2 поступит на первый вход элемента ИЛИ 15 (i-k-l)-ro разряда, выход последнего подключен к вторым входам элементов И 13, 14 этого разряда, произойдет опрос содержимого разряда. Положим, содержимое этого разряда имеет нулевое значение, в этом случае на выходе элемента И 14 появится логический сигнал, который через элемент ИЛИ 15 опросит следующий разряд. Положим, последний п-й разряд регистра 2 имеет единичное значение. В этом случае на выходе элемента И 13-п появится единичный сигнал, который передается на вторые входы элементов И 17-n-l, 17-П-2, 17-п-З, ..., 17-n-J, .,,, 17-n-n. На выходе элемента И 17-П-2, следовательно, появится единичный сигнал,
который через выход произведения матрицы шифруется и попадает на вход сумматора 4, где суммируется с предыдущим значением. Одновременно единичный сигнал через элемент ИЛИ 16 сбрасывает триггер 9-2 в ноль,подается на вторые входы элементов И 8. На выходе элемента И 8-2 в этом случае появится логическая единица,которая через элемент ИЛИ 10 приведет к опросу элементов И 6, 7 (i-k-l)-ro разряда. Если этот разряд имеет нулевое значение, то на выходе элемента И 7 появится единичное значение,которое через элемент ИЛИ 10 опросит следующий разряд. Положим, n-й разряд регистра 1 равен единице. В этом случае на выходе элемента И 6-п появится единичный уровень, который установит триггер 9-п в единичное состояние а последний в свою очередь подключает первые входы элементов И , 17-2-п, ..., 17-j-n, ..., 17-п-пи через элемент ИЛИ 11 разрешит опрос содержимого регистра 2, так как у регистра 2 второй и n-й разряды единичны, то на выходе элемента И 13-2 появится единичный сигнал, подключающий вторые входы элементов- И 17-2-1, 17- 2-3, ..., 17-2-j, ..., 17-2-п, на выходе элемента И 17-2-п появится единичный сигнал, который через вход произведения матрицы преобразится в позиционный код шифратор 3 и поступит на входы сумматора 4, где просум- мируется с содержанием последнего. Произойдет опрос последующих разрядов через элементы И 14„ На выходе элемента И 13-п появится единичный сигнал, что подключает вторые входы элементов И 17-п-1, 17-П-2, 17-п-З, .,., 17-n-j, ..., 17-n-n и приведет к появлению единичного сигнала на выходе элемента И 17-п-п, который известным путем попадет на сумматор 4 и просуммируется в нем. Также единичный сигнал через элемент ИЛИ 16 обнулит триггер 9-п, поступит на вторые входы элементов И 8, что приведет к появлению единичного сигнала на выходе элемента И 8-п, который через элемент ИЛИ 1 2 засвидетельствует окончании процесса умножения, С выходов 22 сумматора 4 можно считывать код произведения.
функциональные возможности изобретения позволят отказаться от устройства преобразования исходных кодов
0
5
0
5
0
5
0
5
0
5
сомножителей в специализированных средствах вычислительной техники,что упростит их, повысит быстродействие и помехоустойчивость.
Формула изобретения
Устройство для умножения, содержащее регистр множителя, регистр множимого, матрицу элементов И из п столбцов и п строк, п-разрядность операндов устройства умножения, о т личающееся тем, что, с целью расширения функциональных возможностей за счет умножения в избыточных двоичных системах счисления, в устройство введены шифратор, накапливающий сумматор, в матрицу элементов И введены 5п элементов И, (2К+3) элементов ИЛИ (К - минимальное количество нулевых разрядов между ближайшими соседними единичными разрядами в представлении чисел в избыточных системах счисления), п счетных триггеров, причем прямой выход 1-го разряда регистра множителя соединен с первым входом (21-1)-го элемента И матрицы (1 1, 2, ..., п), инверсный выход 1-го разряда регистра множителя соединен с первым входом 21-го элемента И матрицы, выход (21-1)-го элемента И матрицы соединен с первым входом (2n+i)-ro элемента И матрицы, со счетным входом 1-го триггера матрицы, с соответствующим входом первого элемента ИЛИ матрицы, второй вход (2n+i)-ro элемента И матрицы соединен с выходом второго элемента ИЛИ матрицы и с входом сброса 1-го триггера матрицы, выход третьего элемента ИЛИ матрицы соединен с выходом окончания процесса умножения устройства, выход 2j-ro элемента И матрицы соединен с вторым входом (2J + + 1)-го и с (2j+2)-ro элемента И
}С + 1
матрицы (j 1, 2,..., -), выход j-ro элемента И матрицы j 2(К+2), 2(К+3), ..., 2(п-1) соединен соответственно с первым входом элемента ИЛИ матрицы с четвертого по К-й, выход элемента ИЛИ матрицы с четвертого по К-й соединен с вторыми входами элементов И матрицы соответственно с 2(п-К) по 2п-й, выходы элементов И матрицы с (2п+1)-го по (Зп-К-1)-й соединены соответственно с вторыми входами элементов ИЛИ мат11
рицы с четвертого по К-й, выход 1-го триггера матрицы соединен с вторыми входами элементов И 1-й строки матрицы, вторые входы первого и второго элемента И матрицы соединены с управляющим входом матрицы, прямой выход 1-го разряда регистра множимого соединен с первым входом (3n+2i- -1)-го элемента И матрицы, инверсный выход 1-го разряда регистра множимого соединен с первым входом (3n+2i)- го элемента И матрицы, выход каждого J-ro элемента И матрицы J (Зп+ +2), (3n+4),.0,,(2K+2)J соединен с вторым входом (j+l)-ro и (j+2)-ro элементов И матрицы, выход каждого четного элемента И матрицы с (Зп + + 2К + 4)-го по (5п-2)-й соединен соответственно с первым входом ментов ИЛИ с (К+4)-го по (2К+3)-й, выход каждого j-ro элемента ИЛИ матрицы (j К+4, К+5,...,2К+3) соединен с вторым входом (3n+2j+l)-ro и
,157157412
по (5п-2К-2)-й соединены соответственно с вторыми входами элементов ИЛИ матрицы с (К+4)-го по (2К+3)-й, выход (3n+2i-l)-ro элемента И матрицы соединен с первыми входами элементов И 1-го столбца матрицы, вторые входы (Зп-И)-го, (Зп+2)-го элементов И матрицы соединены с выходом перво10 го элемента ИЛИ, выходы нечетных элементов И матрицы с (5п-2К-1)-го по (5п-1)-й и ьыход 5п-го элемента И матрицы соединены соответственно с входами второго элемента ИЛИ матJ5 рицы, выходы элементов И матрицы с (Зп-5)-й по Зп-й и выход 2п-го элемента И матрицы соединены соответственно с входами третьего элемента ИЛИ, выходы элементов И строк матри20 цы соединены с соответствующими
входами шифратора устройства умножег ния, выходы шифратора соединены с соответствующими весовыми входами
накапливающего сумматора, выход кото(3n+2J+2)-ro элемента И матрицы,выхо- 25 рого соединен с выходом результата ды элементов И матрицы с (3n+2i-l)-ro устройства умножения.
тов И 1-го столбца матрицы, вторые входы (Зп-И)-го, (Зп+2)-го элементов И матрицы соединены с выходом первого элемента ИЛИ, выходы нечетных элементов И матрицы с (5п-2К-1)-го по (5п-1)-й и ьыход 5п-го элемента И матрицы соединены соответственно с входами второго элемента ИЛИ матрицы, выходы элементов И матрицы с (Зп-5)-й по Зп-й и выход 2п-го элемента И матрицы соединены соответственно с входами третьего элемента ИЛИ, выходы элементов И строк матрицы соединены с соответствующими
входами шифратора устройства умножег ния, выходы шифратора соединены с соответствующими весовыми входами
-/ ffi Vfr-3
Ј5
25
А Агг-Г/ f2-M
/g-jy у улн
адп
u-3
ПГШ: Н
«-fo-2) -o
-M
ПТ
22-3 22-2 22-f

| Устройство для умножения @ -разрядных чисел | 1982 |
|
SU1193667A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Множительное устройство с ферритовой матрицей | 1959 |
|
SU122947A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1990-06-15—Публикация
1988-04-18—Подача