Изобретение относится к области вычислительной техники и предназначено для использования в высокоскоростных параллельно-конвейерных процессорах быстрого преобразования Фурье (БПФ) Виноградовского типа, которые ориентированы на применение в компьютерной томографии, в частности в томографах для обследования высочно-нижне-челюстного сустава.
Цель изобретения - повышение быстродействия устройства для вычисления дискретного преобразования Фурье.
В предлагаемом устройстве для вычисления ДПФ может быть реализовано любое ДПФ вида
Nr-s-1 XS(U)2 Xs(u)(1)
U 0
где Nr-s - обьем ДПФ, реализуемых на s-м шаге алгоритма Винограда, представляющем собой множитель исходного М-точечно- гоДПФ( М-| N2... Mr, r 1); xs(u) xs (u) + jxs (u);
Xs (u), Xs (u) - изменяются в симметричных отрезках -Р, Р. Р - натуральное число; s 0. 1r-1; j vCf,
WNr - s exp( - s)
X-s(v) xs (v) + jxs (v) - отсчеты выходного сигнала ДПФ,
-Ч СО КЗ
со
О1
со
Отделив действительную и мнимую части , запишем (1) в следующей эквивалентной форме:
Гх5 (и) 2 (xt(u)(u)-Sini ; u Q «г si XT s
X/((xf(u)-COs| -X;(u)-Sin ; (2)
ц Q T SI Mf S
V 0,1Nr-s-1
(/
xv
15
20
25
Аппроксимируем константы cos(2jrt/Nr-s) и з1п(2л t/Nr-s) соответственно дробями Wst /Q и Wst /Q, числители которых вычисляются по правилам
Wst 0.соз(2л: t/Nr-s),
WSt Qsin(27r t/Nr-s),
rflet 0,1Nr-s-1; натуральное число;
через х обозначается ближайшее к х целое
число.
Выделив из множества(|
W {Wo,o, WO.QWd .Nr - 1 - 1. Wo.Nr - 1 - 1Wi.o.Wl.oWi.Nr-2 - 1-Wl,Wl,Nr - 2 - 1.
...,Wr-1,o,Wr-1.oWr - 1N1 - 1,Wr - 1,N1 -1}
набор различных его элементов
{w0, wiw A-1} (wiЈ w; i 0, 1A-1;
w, Ј wt, t 0, 1 ..., A-1; t 1 ; Л - объем набора), обозначив через wy0 (s,u,v); wyi (s,u,v), (s,u,v), y0 (s,u,v), 30
yi (s.u.v), )u(s,u,v)Ј {0, 1Л-1}
числители дробей, аппроксимирующих соответственно константы
-sin(2 jruv/Nr-s) sin(2 П I -uv| Nr-s/Nr-s), cos( uv/Nr-s) cos(27ruvl 35 Nr-s/Nr-s), sin(2rcuv/Nr-s) sin(27Tuv W,--A/Nr-s).
Тогда согласно вышеизложенному искомый машинный аналог (2) можно записать в виде;40
, Г« Nr-«--1Ту ЛГу П 1/ч.
л (pj(s-u v)(s u-v))J
Г, Nr-s-1 Гу Лrv l 1
Р Jo(pj(S-U V)+pJ( 45
V О.1.. ,Nr-s-1(3)
где x{j, Хи , X v , Ху - мантиссы отсчетов xs (u), (и), Xs (v), Xs (v) соответственно; 2 - мае- 50 штаб (U - неотрицательное целое число), выбираемый так, чтобы величина xi xu и x u выходили за пределы отрезка (-Р.Р); через x/Q обозначается некоторое целочисленное приближение к 55 дроби x/Q; х-целое число. Без нарушения общности действительные и мнимые составляющие отсчетов исходного N-точечно- го сигнала, а значит и величины XQ (и) и х0 (и) (3) полагаются целочисленными. Целочис0
5
0
5
0
5
0
5
0 5
ленными являются также мантиссы Xu , x i , Xi , Ху для всех s 0,1г-1. Следовательно, они являются элементами диапазона {-Р, -Р+1,..., Р} и имеют порядок 0 0.
Для реализации базовых соотношений (3) используется МСС с основаниями mi, m2, .... mk удовлетворяющими условиям М mi гп2... mk PQq V и mk 2m0 + K-2; m0 K-2 (где q max {N1, N2, ..., Nr}).
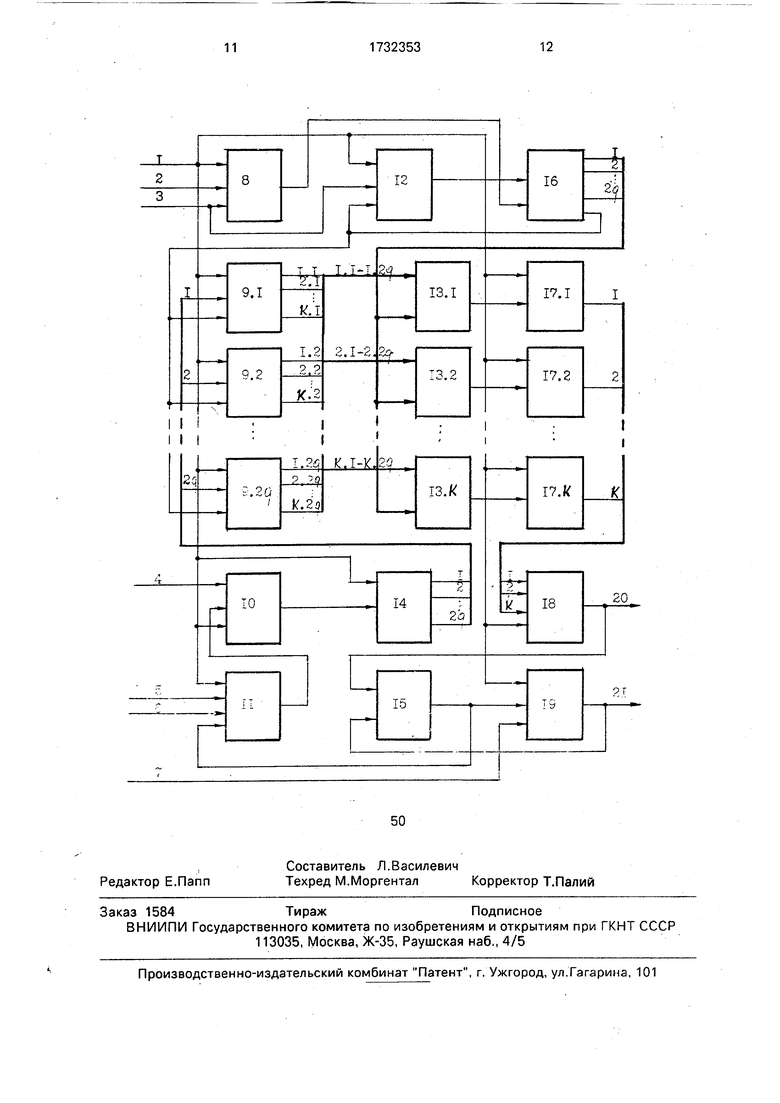
На чертеже приведена структурная схема предлагаемого устройства для вычисления дискретного преобразования Фурье (ДПФ).
Устройство для вычисления ДПФ содержит тактовый вход 1, вход 2 задания номера шага алгоритма, первый установочный вход 3, информационный вход 4, четвертый 5, второй 6 и третий 7 установочные входы, регистр S номера шага разрядностью 1од2г, входные регистры 9.1-9.2q разрядностью k
L 2} bjбит (bi log2mi ; через
| - |
х обозначается ближайшее к х справа целое число), блок 10 преобразования двоичного кода в код модулярной системы счисления, первый регистр 11 константы сдвига, счетчик 12 тактов, группы блоков постоянной 13,1-13.К памяти, блок 14 задержки, блок 15 постоянной памяти константы сдвига, блок 16 постоянной памяти коэффициентов, блоки 17.1-17.К суммирования соответственно по модулям mi, ГП2mk, блок
18 преобразования кода модулярной системы счисления в двоичный код, второй регистр 19 константы сдвига, выходы мантиссы 20 и порядка 21 устройства.
Блок 10 осуществляет преобразование А-битовых двоичных кодов мантисс Хи и x u в модулярный код величин Xu и x u .Данный блок представляет собой известное устройство, выполняющее одно преобразование за + 1 такт, где Т log2N ; /n - число групп двоичных разрядов в преобразуемых А-битовых кодах ( А- разрядность промасш- табированных значений соответствующих мантисс), Обращение к блоку 10 можно производить ежетактно. Первый вход преобразователя 10 является информационным входом 4 устройства. Второй вход подключен к выходу регистра 11, а выход заведен на вход блока 14 задержки.
Тактовый вход блока 10 объединен с тактовыми входами регистров 8,9.1-9.2q, 11 и 19 блока 14 задержки, блоков 17.1-17.К суммирования, блока 18 преобразования кода модулярной системы счисления в двоичный код со счетным входом счетчика 12 тактов и подключен к тактовому входу 1 устройства.
Блок 18 преобразования кода модулярной системы счисления в двоичный код является известным устройством конвейерного типа, осуществляющим одно преобразование за (Т + 3) такта (Т JlogakQ. причем, обращение к преобразователю можно производить ежетактно. Блок 18 по информационным входам соединен с выходами блоков 17.1-17.К суммирования. Его выход является выходом 20 мантиссы устройства, при этом старшие d разрядов выхода заведены на первый адресный вход блока 15 постоянной памяти.
Счетчик 12 тактов является (Tq + разрядным (Tq iog2qD и имеет два входа установки в нуль. Наличие единичного сигнала на любом из них обнуляет содержимое счетчика в момент окончания тактового импульса на счетном входе счетчика. Первый вход установки в нуль счетчика 12 объединен с входом разрешения записи регистра 8 номера шага и подключен к первому установочному входу 3 устройства. Второй вход установки в нуль объединен с входами разрешения записи регисров 9.1-9.2q и подключен к (2q + 1)-му выходу блока 16 постоянной памяти. Запись информации в регистры 9.1-9.2q осуществляется при наличии единичного сигнала на их входах разрешения записи. Выход счетчика 12 заведен на первый вход блока 16 постоянной памяти.
Группа блоков 13.1 (,2К) постоянной памяти состоит из 2q одинаковых блоков постоянной памяти емкостью (2bi + 1|од2сЛ)Ь| бит. В каждом из этих блоков постоянной памяти по адресу f + t 2Bi записывается вычет mi для
всех % 0, 1mi-1, t 0, 1Л-1, где
через lAlm обозначается наименьший неотрицательный вычет, сравнимый с величиной А по модулю т. Первый адресный вход j-ro блока постоянной памяти группы 13.1 подключен к i-му выходу регистра 9.j Q 1,
22q), вторые адресные входы j-x блоков
постоянной памяти всех групп объединены и подключены к j-му выходу блока 16, а выход j-ro блока постоянной памяти подключен к одноименному входу блока 17.1.
Блок 14 задержки представляет собой цепочку из 2q-1 регистров разрядностью L бит. Вход первого регистра подключен к первому выходу блока 14 задержки, а выход 1-го регистра является (I + 1)-м выходом блока задержки (1 1,22q-1). Выходы блока
14 задержки с первого по(2р)-й подключены к информационным входам соответственно регистров 9.1-9.2q. Обращение к блоку задержки может осуществляться ежетактно.
Блок 15 постоянной памяти ко CTat -ы сдвига обладает емкостью 2d + °92ai loQ.d бит (d 1). В его память по адресу х + I 2 записывается величина тах{(х), ё}
для всех х 0,12d - 1 и I1 0, 1d-1, /где ((х)-номер самой младшей цифры двоичного кода (xd-ixd-zх0)2 числа х, удов- /
летворяющей условию xi xi(x) при каждом i l(x). Второй адресный вход блока 15
0 подключен к выходу регистра 19, являющемуся выходом 21 порядка устройства. Информационные входы регистров 11 и 19 объединены и подключены к выходу блока 15. Вход разрешения записи регистра 11 и
5 входы установки в нуль регистров 11 и 19 подключены соответственно к четвертому 5, второму б и третьему 7 установочным входам устройства. Запись в регистр 11 осуществляется при поступлении единичного
0 сигнала на установочный вход 5 устройства. Запись в регистр 19 осуществляется ежетактно. Единичные сигналы на установочных входах 6 и 7 обнуляют содержимое соответственно регистров 11 и 19.
5 Блок 16 постоянной памяти обладает емкостью 24og2it + тч + 1) х 2q log2 Л + 1). В его память по адресу (v + У- Tq + i)s) записывается двухкомпонентный набор величин
0
Ih(s,v) xz-h(s,o,v),)-h(s1o,v)1
У2-ь(8,1лО,уз -h(S,1,V),...,73-h(S,Nr -s - 1.V),
У.У,..
j-я из которых поступает на j-й выход Q 1, 2q) блока 16. Здесь у - номер нуля множества
{WQ, wiwA - 1}, т.е. константы Wy 0.
На (2д+1)-й выход блока 16 поступает из ячейки с вышеуказанным адресом величина (1 - 2Nr-s - V-1Q, которая обеспечивает для счетчика 12 подсчет числа тактов по подулю 2Nr-s. Второй адресный вход блока 16 постоянной памяти подключен к выходу регистра 8 номера шага. Информационный вход последнего подключен к входу 2 задания номера шага. Запись числа в регистр 8 осуществляется по окончанию такта при наличии единичного сигнала на входе разрешения записи.
Блоки суммирования по модулю 17.1- 17.К являются известными устройствами. Они имеют (Tq + 1)-каскадную параллельно- конвейерную структуру, благодаря чему об- ращение к ним можно производить ежетактно.
Работа предлагаемого устройства для вычисления ДПФ.
Процесс выполнения ДПФ, описываемого выражением (3), можно разбить на
5
5
0
5
два этапа. В ходе первого этапа мантиссы XNr-s-1, XNr-s-i, x A, Хо действительных и мнимых составляющих отсчетов входного сигнала ДПФ последовательно от такта к такту, начиная с нулевого, в указанном порядке подаются на первый вход блока 10, на второй вход которого из регистра 11 ежетактно поступает константа сдвига Hs, отвечающая текущему (s-му) шагу алгоритма Винограда. Перед началом нулевого шага алгоритма регистр 11 по сигналу 2.2 1 с входа 6 устройства обнуляется (0 О), а на последнем О/г + 2Nr-s + Tq + Т + 5)-м такте каждого шага в регистр 11 по сигналу ZQ 1, поступающему с входа 5 устройства, записывается константа, формируемая так, как это изложено ниже, на входе блока 15 постоянной памяти. На 1)-м такте каждого на установочном/входе 3 устройства появляется сигнал Zi 1, по которому в конце этого такта в регистр 8 занесется значение s, поступавшее на вход 2 задания номера шага алгоритма, а содержимое счетчика 12 тактов обнуляется. С конца (Т/г+ 1)-го такта, где Tfi log2/ , (i- число групп двоичных разрядов в преобразуемых , Я-битовых кодах, в блок 14 задержки с выхода блока 10 ежетактно начнутгюступатьмодулярные коды (МК) величин XNr-s-1, xW-s-1хо , Хо и
по истечении ( 2Nr-s)-ro такта полученные МК по единичному сигналу с (2q+1)-ro выхода блока 16 передаются в регистры 9.1- 9.2Nr-s, модулярный код (2Nr-s -1 +1)-го элемента последовательности запоминается в
регистре 9.t(t 1, 22Nr-s).
Второй этап процесса реализации выражений (3) так же, как и первый, состоит из 2Nr-s тактов. В ходе (2v + h)-ro цикла, начинающегося с ( Т/г+ 2Nr-s + 2v + h)-ro такта
(v { О, 1Nr-s-1; h {1, 2}) на первый и
второй входы группы блоков 13.1 (I 1, 2
К) подаются соответственно 2р-компонентные наборы величинл .
i ii ii
лй iXolmi, IXolmiI XNr-s-1 I ml,
I XNr-s-1 I mi, R2Nr-1R2q-1 иГц (S, v),
где Rt - t-я цифра МК, записанного в регистре 9.t(t 2Nr-s + 1,2Nr-s + 22q). В результате во входные регистры блоков 17.1 суммирования вычетов с выхода группы блоков 13.1 постоянной памяти поступит набор вычетов
(s,0,v)Li, IXoWy3-h(s,0,v)lmi
I XNr-s-1 Wy2-h(s, Nr-s-1, v)l mi. I XNr-s-i Wya-h (s.Nr-s-1. v) I mi, 00
для всех i 1, 2 К и по окончании
( 2Nr-s + 2v + h + Tq + 1)-ro такта блоки
17.1-17.Ксформируют МКчисла yv при h 1 и числа yv при h 2 по правилу
nrf
,
5 Yv 2 (xuWyi(s,u,v)+XuWy2(s,u,v))
10
yv- 2 (xuWy0(S,UAO+XuWyi(s,u,v)).
Полученный МК на следующем такте поступает в блок 18 преобразования, Двоичные
А-разрядные коды результатов масштабирования величин yv и yv на масштаб Q, т.е. искомые мантиссы Ху и Ху действительной и мнимой составляющих v-ro комплексного отсчета выходного сигнала выполняемого ДПФ (формула (3) будут получены блоком 18 соответственно на (Т//+ 2Nr-s + 2v +
+Tq + T + 5) M H07/+2Nr-s + 2v + Tq + T + 6)
м тактах. Мантисса, полученная по истечении (Т/г + 2Nr-s +2v+Tq+T+h+ 4)-ro такта,
снимается с выхода мантисс AY в следующем такте. При этом ее d-битовая старшая часть ду вместе с содержимым регистра RGe подаются на адресные входы блока 12 и из его памяти по адресу gv + e 2d считывается величина max{l(gv), e }, которая запоминается в регистре 19. В момент появления на выходе блока 18 преобразования мантиссы действительной части нулевого комплексного отсчета выходного сигнала первого из
ДПФ, выполняемых на s-м шаге алгоритма Винограда (s 0, 1,..., г-2), т.е. по окончании (T/j+2Nr-s + Tq + T+ 5)-го такта данного шага, регистр 19 обнуляется по сигналу Za 1 с входа 7 устройства. Поэтому согласно вышеизложенному после выполнения последнего из ДПФ s-ro шага на выходе блока 15 постоянной памяти сформируется константа сдвига U+1 для (s+1)-ro шага. Полученная константа записывается как в регистр 19,
откуда она поступает на выход 21 порядка устройства, так и по сигналу ZA 1 в регистр 11. Действительные и мнимые составляющие всех отсчетов выходного сигнала исходного N-точечного ДПФ, вычисляемое в ходе
заключительного шага алгоритма Винограда, имеют общий порядок: h + la + ... + 1м.
Заметим, что отдельные ДПФ объема Nr-s в описываемом устройстве осуществляются за T(Nr-s) 4Nr-s + Т/г + Tq + Т + 5 тактов, t
При этом реализация нбвого ДПФ данного объема может быть начата по истечении (2Nr-s)-ro такта текущего преобразования, т.е. частота обращения к устройству на s-м шаге алгоритма Винограда составляет 1/2(2Мг-з)Тмт, где ТМт длительность модульного такта.
Если, например, Nr-s 4, то f 1/8ТМт, что существенно выше частоты обращения известного устройства, составляющей 1/13ТМт. Поскольку предлагаемое устройство способно выполнять любое ДПФ объема, не превышающего q, то сфера его применения существенно шире, чем у известного.
Формула изобретения Устройство для вычисления дискретного преобразования Фурье, содержащее первый и второй регистры константы сдвига, блок постоянной памяти констант сдвига, блок преобразования кода модулярной системы счисления (МСС) в двоичный код и блок преобразования двоичного кода в код модулярной системы счисления, первый и второй информационные входы которого подключены соответственно к информационному входу устройства и выходу первого регистра константы сдвига, тактовый вход которого подключен к тактовому входу устройства и соединен с тактовыми входами блока преобразования двоичного кода в код модулярной системы счисления, второго регистра константы сдвига и блока преобразования кода модулярной системы счисления в двоичный код, выход которого является выходом мантиссы устройства и подключен к первому адресному входу блока постоянной памяти константы сдвига, второй адресный вход которого подключен к выходу второго регистра константы сдвига, выход которого является выходом порядка устройства, отличающееся тем, что, с целью повышения быстродействия, в него введены регистр номера шага, счетчик тактов, блок постоянной памяти коэффициентов, 2q (q - объем преобразования) входных регистров, К групп блоков постоянной памяти (К- число оснований модулярной системы счисления) по 2q блоков в каждой, К блоков суммирования по модулю соответственно mi,
maтк, блок задержки, j-й (j 1,2q) вы 1д
которого подключен к информационному входу j-ro входного регистра, i-й (i TTR) выход которого подключен к первому адресному входу j-ro блока постоянной памяти i-й группы, выход которого подключен к j-му информационному входу блока суммирования по модулю mi, выход которого подключен к i-му информационному входу блока
преобразования кода модулярной системы счисления в двоичный код, выход блока преобразования двоичного кода в код модулярной системы счисления подключен к информационному входу блока задержки,
тактовый вход которого соединен с тактовыми входами всех входных регистров, тактовыми входами всех блоков суммирования по модулю, счетным входом счетчика тактов, тактовым входом регистра номера шага и
подключен к тактовому входу устройства, первый установочный вход которого подключен к установочному входу счетчика тактов и входу разрешения записи регистра номера шага, выход которого подключен к
второму адресному входу блока постояндрй памяти коэффициентов, М-й выход (М 1,2q) которого подключен к второму адресному входу М-го блока постоянной памяти i-й группы, информационный выход счетчика
тактов подключен к первому адресному входу блока постоянной памяти коэффициентов, (2q + 1)-й выход которого подключен к входу обнуления счетчика тактов и входу разрешения записи j-ro входного регистра,
выход блока постоянной памяти констант сдвига подключен к информационным входам первого и второго регистров констант, сдвига, установочные входы которых подключены соответственно к второму и третьему установочным входам устройства, четвертый установочный вход которого подключен к входу разрешения записи первого регистра константы сдвига, а вход задания номера шага устройства подключен к информационному входу регистра номера шага.




| название | год | авторы | номер документа |
|---|---|---|---|
| Арифметическое устройство для процессора быстрого преобразования Фурье | 1981 |
|
SU1042028A1 |
| Устройство для нормализации чисел в модулярной системе счисления | 1986 |
|
SU1332317A1 |
| Устройство для умножения чисел в модулярной системе счисления | 1986 |
|
SU1352483A1 |
| Арифметическое устройство в модулярной системе счисления | 1987 |
|
SU1432517A1 |
| Устройство для преобразования непозиционного кода в позиционный код | 1987 |
|
SU1510097A1 |
| Устройство для сложения и вычитания чисел с плавающей запятой | 1986 |
|
SU1411742A1 |
| Устройство для нормализации чисел в модулярном коде | 1984 |
|
SU1242942A1 |
| Арифметическое устройство для процессоров быстрого преобразования Фурье | 1983 |
|
SU1116434A1 |
| Устройство для вычисления дискретного преобразования Фурье в модулярной системе счисления | 1988 |
|
SU1633423A1 |
| Устройство для формирования интегральных характеристик модулярного кода | 1984 |
|
SU1216777A1 |
Изобретение относится к вычислительной технике и предназначено для использования в высокоскоростных параллельно-конвейерных процессорах быстрого преобразования Фурье Виноградовского типа. Цель изобретения - повышение быстродействия устройства для вычисления дискретного преобразования Фурье (ДПФ). Поставленная цель достигается тем, что в устройстве обеспечивается реализация ДПФ любого объема, не превосходящего заданного значения, путем использования однократных модульных умножителей табличного типа. Устройство для вычисления ДПФ содержит блок преобразования двоичного кода в код модулярной системы счисления, два регистра константы сдвига, блок постоянной памяти константы сдвига, блок преобразования кода модулярной системы счисления в двоичный код, счетчик тактов, регистр номера шага, входные регистры, блок постоянной памяти коэффициентов, группы блоков постоянной памяти, блоки суммирования по модулям и блок задержки. 1 ил. (Л с

| Устройство для быстрого преобразования Фурье | 1985 |
|
SU1290350A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Арифметическое устройство для процессора быстрого преобразования Фурье | 1981 |
|
SU1042028A1 |
Авторы
Даты
1992-05-07—Публикация
1990-04-11—Подача