Известны способы измерения постоянной Бремени объекта, описываемого дифференциальным уравнением первого порядка. Они основаны на подаче испытательного сигнала на входы объекта и модели и на изменении постоянной времени модели но нелииейному закону.
Предлагаемый способ отличается от известных тем, что он ускоряет процесс измерения постоянной времени н, кроме того, расгииряет пределы измерения ее благодаря изменению постоянной времени модели по разрывному гиперболическому закону линейно меняющимся испытательным сигналом. Результат сравнения сигналов с выходов модели и объекта интегрируют и в момент равенства этих сигналов измеряют напряжение на выходе интегратора. Напряжение обратно пропорционально постоянной времени объекта. В момент равенства нулю величины, обратной постоянной времени модели, изменяют структуру модели, инвертируя знак производной выходного сигнала с модели.
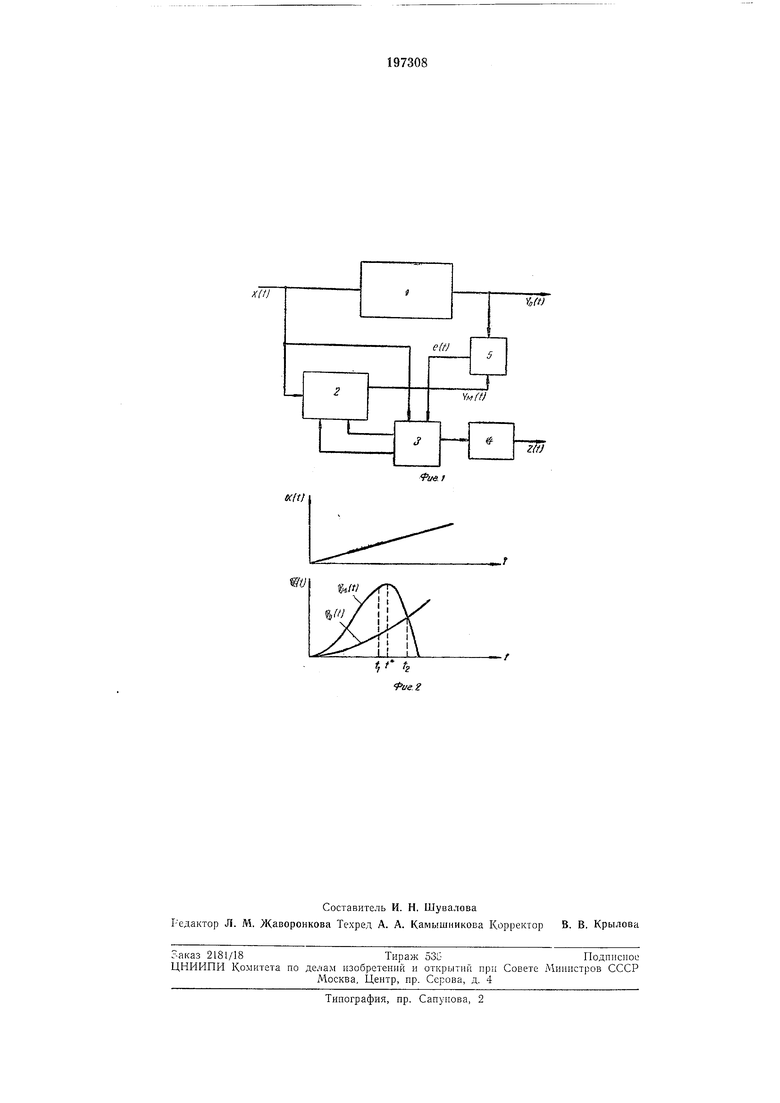
Блок-схема на фиг. 1 поясняет описываемый способ; фиг. 2 изображает кривые времени модели и объекта.
изменяют постоянную времени модели по разрывному гиперболическому закону
м(()
а - bt
И интегрируют постоянное напряжение в блоке 4 измерительного интегратора. В момент
/ -, когда постоянная времени модели
имеет разрыв, при помощи блока управления изменяют структуру модели так, чтобы изменить знак производной ее выходного сигнала, т. е. делают модель неустойчивой. Выходные сигналы объекта и модели сравнивают в блоке сравнения 5, нри помощи которого фиксируют момент времени, когда сравниваются выходные сигналы объекта н модели. В этот момент сигналом блока управления прекращают интегрирование постоянного напряжения в блоке 4 и определяют значенне измеряемого параметра как величину, обратную выходному сигналу измернтель|Юго интегратора.
Выходные сигналы объекта
, kx.(t)
25 с постоянной времени м(0. изменяемой по разрывному гиперболпческому закону (1), при пилообразном входном сигнале имеют соответственно вид y,(t) ± . y(f) I Mfe В переходных нроцессах объекта и модели можно отметить характерные момент1 1 времени: /1 - момент времени, когда постоянная времени модели равна постоянной времени объекта, т. е. ИЛИ /1
/2 - момент времеии, когда ошибка e(t) ((0 равна нулю, что с точностью до постоянного множителя кс означает. it - i е( 1 в 1-е Из выражения (3) следует, что измеряемое: значение Т легко определяется, если известна величина t-. Величина 9 -т может быть просто определена, если известно время 2, которое легко определяется при помощи сравнивающего устройства. Отношение моментов времени t-i и /i как функция параметров модели и объекта может быть вычислено для различных значений этих параметров из уравнения, которое получается путем замены переменных4 уравнении (4). Заменив переменные под интегралом, получим следующее уравнение относительно интересующей нас функции: Ф({/в) + -2.-) (т-1) , «2г где -; { 1 а ; 2« Г,, (0) 2 С - Ф (U) . г- е dx- интеграл вероятности. Исследование зависимостей в(у) показывает, что кривые 0 (Y) при любых значениях параметра е лежат ниже линии ,5, начиная с некоторого значения у у(г), кривая
нал блока 4 будет численно равен
7/4Г JOi-ni ,J.
Z (i) - a - /2 : a-bti - - ,
„Q Qt; ,Q 45 50 55 60 0(у) может быть аппроксимирована прямой, т. е. если , , Q.. с любой желаемой точностью. Таким образом, в значительном диапазоне выполпено простое соотношение Если у 3е, то это соотношение выполняется с точностью не хуже 1%. Отсюда ясно, что если в блоке измерительного интегратора выставить начальное условие, численно равное в каком-либо масштабе величине , подать на вход его постоянное напряжение, например, величины Е, установить коэффициент усиления интегратора, численно равный - -::--, то в момент /2 выходной сигТ. е. обратной величине измеряемого параметра. Изменяя структуру модели в момент/ - так, чтобы изменить знак производной ее выходного сигнала (при реализации модели на аналоговой машине и осуществлении закона м(0 с помощью потенциометра это а - Ы изменение требует переключения схемы набора модели), можно полностью использовать диапазон измерения постоянной времени модели от - до CN5, в результате чего пределы измерения оказываются равными cv. Иредмет изобретения Способ измерения постоянной времени объекта, описываемого дифференциальным уравнением первого порядка, основанный на подаче испытательного сигнала па входы объекта и модели и иа изменении постоянной времени модели по нелинейному закону, отличающийся тем, что, с целью расширения пределов измерения постоянной времени объекта и повышения быстродействия процесса измерения, линейно меняющимся испытательным сигналом изменяют постоянную времени модели по разрывному гиперболическому закону, интегрируют результат сравнения сигналов с выходов модели и объекта и измеряют в момент равенства этих сигналов напря;кение на выходе интегратора, обратно пропорциональное постоянной времени объекта, причем в момент равенства нулю величины, обратной постоянной времени модели, изменяют структуру модели, инвертируя знак
K(tl

| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ИМПУЛЬСНЫМ СТАБИЛИЗАТОРОМ НАПРЯЖЕНИЯ | 2003 |
|
RU2239225C2 |
| СПОСОБ ФОРМИРОВАНИЯ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ | 1970 |
|
SU276207A1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОСТОЯННОЙ ВРЕМЕНИ ОБЪЕКТА | 1966 |
|
SU185589A1 |
| СТЕНД ДЛЯ ОПРЕДЕЛЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ НАВИГАЦИОННЫХ ДАТЧИКОВ | 1972 |
|
SU342198A1 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ РОТОРА РЕАКТИВНОЙ ГИДРАВЛИЧЕСКОЙ ТУРБИНЫ И ПИД-РЕГУЛЯТОР ЧАСТОТЫ ВРАЩЕНИЯ СИЛЬНОГО ДЕЙСТВИЯ | 2021 |
|
RU2781087C1 |
| СПОСОБ УПРАВЛЕНИЯ ИМПУЛЬСНЫМ СТАБИЛИЗАТОРОМ | 2002 |
|
RU2238583C2 |
| Способ стабилизации положения плазменного шнура в токамаке | 1983 |
|
SU1119490A1 |
| Устройство для идентификации параметров систем управления | 1979 |
|
SU885976A1 |
| Устройство для измерения рассеяния энергии | 1980 |
|
SU928250A1 |
| Способ измерения несущей частоты колебательных объектов | 1978 |
|
SU789997A1 |

t,f t, Pue.
Авторы
Даты
1967-01-01—Публикация