Предложение относится к вычислительной технике.
Известно устройство свертки двоичного числа в вычет по произвольному модулю, содержащее регистр преобразуемого числа и пирамиду матриц для сложения вычетов, выполненных на элементах конъюнкции, в котором триггеры регистра и матрицы каждой ступени пирамиды разбиты на пары, причем парафазные выходы первого и второго триггера каждой пары подключены соответственно к горизонтальным и вертикальным входным шинам матрицы первой ступени пирамиды, а выходные шины первой и второй матриц каждой пары подключены соответственно к горизонтальным и вертикальным входным шинам матрицы следующей ступени пирамиды.
В известном устройстве пары объединены по признаку соседства.
Предложенное устройство отличается тем, что в нем соединены в пары триггеры тех разрядов регистра преобразуемого числа, наименьшие неотрицательные вычеты весов которых одинаковы, и матрицы каждой ступени пирамиды, формирующие результаты из одинаковой совокупности возможных значений, а при наличии вычетов, равных по величине, но противоположных по знаку, среди абсолютных наименьших вычетов весов разрядов преобразуемого числа, в пары соединены триггеры тех
разрядов регистра преобразуемого числа, абсолютные наименьшие вычеты которых равны по абсолютной величине, и те матрицы каждой ступени пирамиды, совокупность возможных
значений формируемых результатов одной из которых равна сумме по принятому модулю возможных значений формируемых результатов другой матрицы с произвольной фиксированной константой.
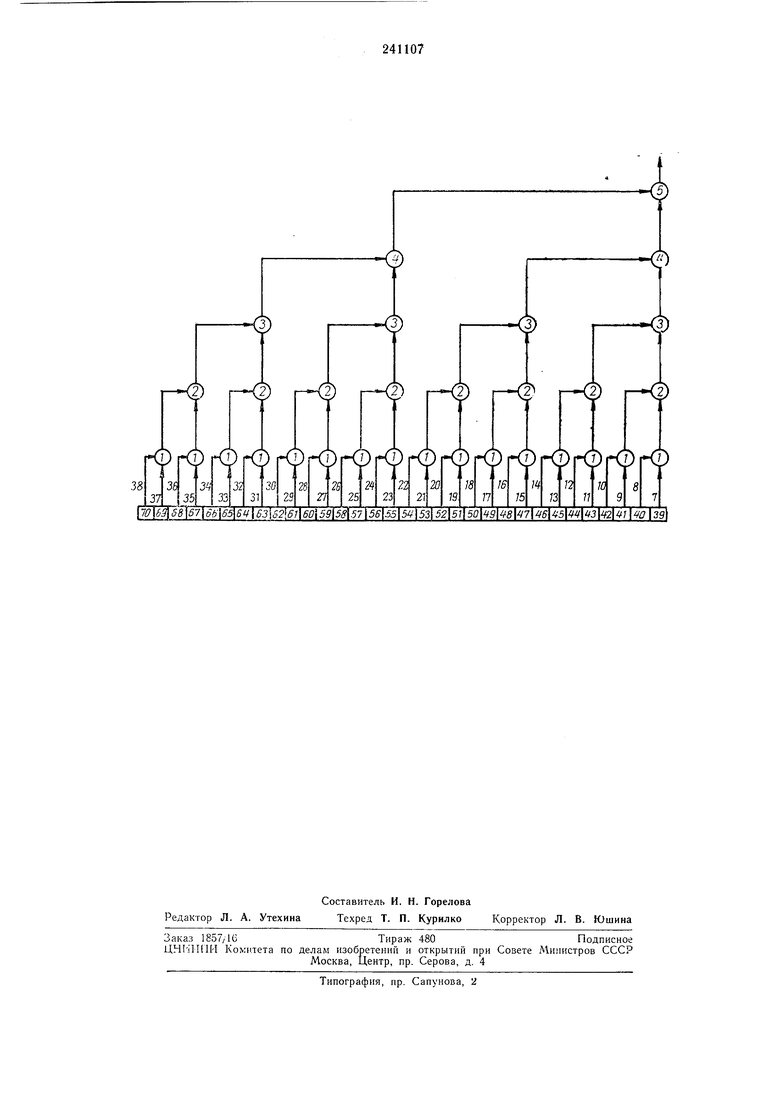
Обобщенная схема устройства свертки приведена на чертеже.
Устройство содержит матрицы конъюнктивных элементов 1 - 5 соответственно первой- пятой ступеней пирамиды, выходные шины 6
преобразователя свертки, пары входных шин 7-38 матриц первой ступени (горизонтальных и вертикальных), соединенные с выходами триггеров 39-70.
Ком.мутацию входных и выходных шин
матриц в преобразователе можно пояснить на примере свертки целого числа.
Пусть т 17. Парафазные выходы триггеров разрядов с номерами 0,8, 16,24 (наименьшие неотрицательные вычеты соответствуюших
весов по модулю 17 равны I) подают на входы 7-10 матриц первой ступени, выходы триггеров разрядов с номерами /, 9, 17, 25 (вычеты равны 2) - на входы 11, 12, 13, 14 и т. д. Количество различных результатов на выхоНапример, на выходе матриц, имеющих входы 7, 8, возможны следующие результаты: О, 1, 2 (т. е. 0X20+0X28 0,1X20+0X28 0X20+1 X Х28 1,1X2 +1X28 2). Следовательно, все матрицы второй ступени пирамиды должны иметь размерность 3X3. Так как на входы матриц второй ступени подают выходы тех матриц первой ступени, которые формируют результаты из одинаковой совокупности возможных значений, то количество различных результатов на выходе матрицы 2 будет равно пяти. В частности, для матрицы 2, связанной с матрицами первой ступени, имеющими входы 7-10, возбуждение выходов ассоциируется с получением одного из результатов О, 1, 2, 3,4 за счет комбинирования величин О, 1, 2, подаваемых на ее горизонтальные и вертикальные входы. Аналогично для матрицы 2, связанной с матрицами первой ступени, имеющими входы 11-14, могут быть получены значения результатов О, 2, 4, 6, 8. Таким образом, в предложенном устройстве матрицы третьей ступени имеют размерность 5X5, причем среди них нельзя найти такие, которые формируют результаты из одинаковой совокупности возможных значений. В частности, для матрицы 3, связанной с ранее упомянутыми матрицами второй ступени, возбуждение выходов соответствует получению одного из результатов О, 1, 2... 12 за счет комбинирования величин О, 1, 2, 3, 4, подаваемых на ее вертикальные входы, и величин О, 2, 4, 6, 8, подаваемых на горизонтальные входы. Очевидно, что размерность матриц четвертой ступени 13X13, а пятой- 17X17.
В случае, если среди абсолютных наименьщих вычетов весов разрядов преобразуемого числа можно выделить вычеты, равные по величине, но противоположные по знаку (это невозможно сделать, например, для модулей вида 2-1, где п - целое число), применим другой метод коммутации, при котором в пары группируют триггеры тех разрядов регистра преобразуемого числа, абсолютные наименьшие вычеты весов которых равны по абсолютной величине, и те матрицы каждой ступени пирамиды, совокупность возможных значений формируемых результатов одной из которых может быть получена из всевозможных значений формируемых результатов другой путем слолсения (по модулю т) последних с произвольной, но фиксированной константой.
В частности, для модуля 17 удается среди абсолютных наименьших вычетов весов разрядов преобразуемого числа выделить такие, которые равны по абсолютной величине, независимо от того, одинаковы они или противоположны по знаку.
Следовательно, возможен следующий вариант построения пирамиды преобразователя.
Выходы триггеров разрядов с номерами О, 8, 16, 24 подключают соответственно к 7-10 выходам матриц первой ступени; выходы 4, 12,
20, 28 триггеров - к //-14 входам и т. д. Каждая из матриц первой ступени пирамиды, как и ранее, имеет размерность 2X2 и количество выходов, равное трем; матрицы второй ступени имеют размерность 3X3 и по пять выходных щин, а размерность матриц третьей ступени, как и ранее, 5X5, однако у каждой из них девять выходов. Действительно, совокупность возможных результатов на выходе
матрицы 2, связанной с матрицами первой ступени, имеющими входы 7-10, будет О, 1, 2,3,4, а на выходе матрицы 2, связанной с матрицами первой ступени, имеющими входы 11-14, будет -4,-3,-2,-1,0. Элементы первой совокупности могут быть получены из элементов второй путем суммирования последних с константой, равной 4. Это является достаточны.м условием, приводящим к тому, что количество различных результатов на выходе рассматриваемой матрицы 3 будет 9 (а не 13, как при предыдущем способе коммутации): 0,±1,+ ±2,+3,±4. Итак, размерность матриц четвертой ступени оказывается равной 9X9.
Матрица 5, расположенная Б пятой ступени
пирамиды, будет иметь размерность 17X17.
Предмет изобретения
Устройство для свертки двоичного числа в
вычет по произвольному модулю, содержащее регистр преобразуемого числа и пирамиду матриц для сложения вычетов, выполненных на элементах конъюнкции, в котором триггеры регистра и матрицы каждой ступени пирамиды
разбиты на пары, причем парафазные выходы первого и второго триггера каждой пары подключены соответственно к горизонтальным и вертикальным входным шинам матрицы первой ступени пирамиды, а выходные шины первой и второй матриц каждой пары подключены соответственно к горизонтальным и вертикальным входным шинам матрицы следующей ступени пирамиды, отличающееся тем, что, с целью упрощения и повышения надежности, в
нем соединены в пары триггеры тех разрядов регистра преобразуемого числа, наименьшие неотрицательные вычеты весов которых одинаковы, и матрицы каждой ступени пирамиды, формирующие результаты из одинаковой совокупности возможных значений, а при наличии вычетов, равных по величине, но противоположных по знаку, среди абсолютных наименьших вычетов весов разрядов преобразуемого числа, в пары соединены триггеры тех разрядов регистра преобразуемого числа, абсолютные наименьшие вычеты которых равны по абсолютной величине, и те матрицы каждой ступени пирамиды, совокупность возможных значений формируемых результатов одной из
которых равна сумме по принятому модулю возможных значений формируемых результатов другой матрицы с произвольной фиксированной константой.

| название | год | авторы | номер документа |
|---|---|---|---|
| Преобразователь числа в модулярный код | 1987 |
|
SU1444961A1 |
| УСТРОЙСТВО ДЛЯ ОБНАРУЖЕНИЯ ПЕРЕПОЛНЕНИЯ ДИНАМИЧЕСКОГО ДИАПАЗОНА, ОПРЕДЕЛЕНИЯ ОШИБКИ И ЛОКАЛИЗАЦИИ НЕИСПРАВНОСТИ ВЫЧИСЛИТЕЛЬНОГО КАНАЛА В ЭВМ, ФУНКЦИОНИРУЮЩИХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2011 |
|
RU2483346C1 |
| Устройство цифровой двумерной свертки | 1988 |
|
SU1647585A1 |
| ОТКАЗОУСТОЙЧИВЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2018 |
|
RU2680035C1 |
| ДВУХУРОВНЕВОЕ УСТРОЙСТВО ИСПРАВЛЕНИЯ ОШИБОК | 1992 |
|
RU2037891C1 |
| Устройство для формирования и хранения вычетов чисел по модулю три | 1983 |
|
SU1109755A1 |
| ПРЕОБРАЗОВАТЕЛЬ КОДОВ ИЗ ОСТАТОЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ПОЛИАДИЧЕСКУЮ | 1973 |
|
SU407301A1 |
| УСТРОЙСТВО ДЛЯ ПОЛУЧЕНИЯ КОНТРОЛЬНОГО КОДА ЧИСЛА | 1967 |
|
SU190657A1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ АНАЛОГОВОЙ ВЕЛИЧИНЫ В КОД | 1990 |
|
RU2020746C1 |
| САМОПРОВЕРЯЕМЫЙ СПЕЦИАЛИЗИРОВАННЫЙ ВЫЧИСЛИТЕЛЬ СИСТЕМ БУЛЕВЫХ ФУНКЦИЙ | 2012 |
|
RU2485575C1 |


Даты
1969-01-01—Публикация