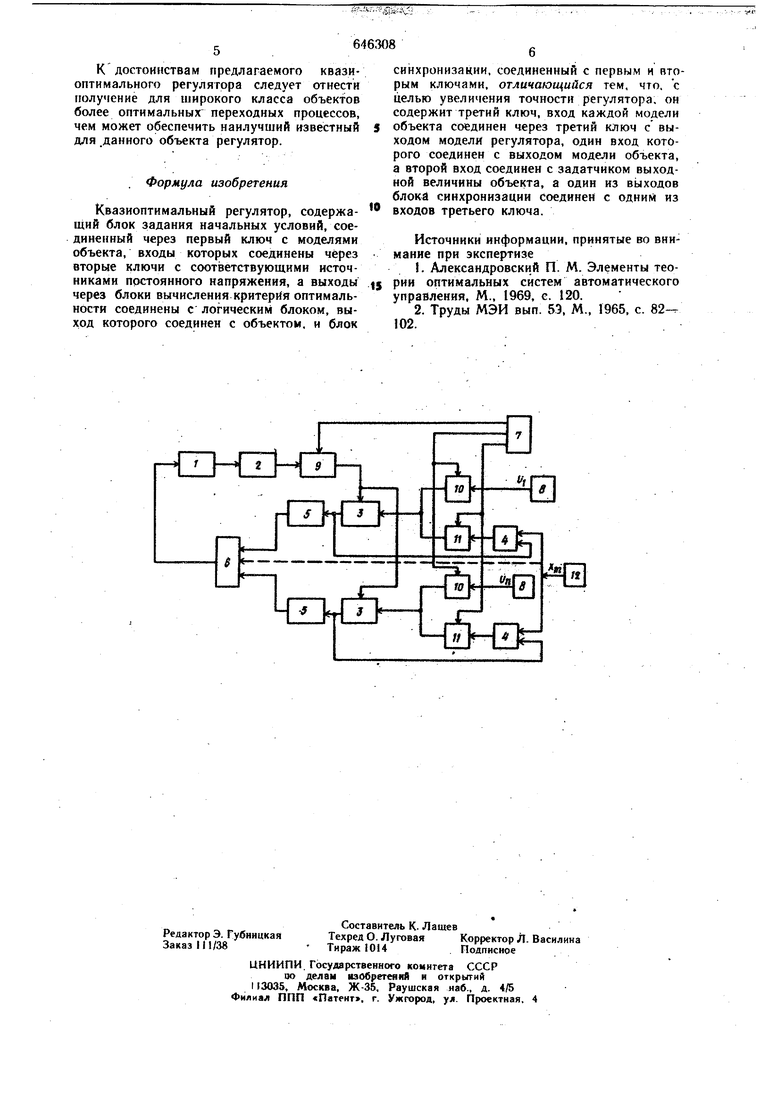
Предлагаемое устройство относится к автоматике и может быть иснользовано при управлении Динамическими объектами. Известны квазиоптимальные регуляторы с.использованием модели объекта, работающей в ускоренном масштабе времени, для прогноза на отрезок времени фазовых коор.динат объекта для некоторых значений уп. равляющего воздействия 1. Малая точИость известных регуляторов - их недостаток. Наиболее близким по техническому исполненню устройством является регулятор, содержащий блок задания начальных условий, соединенный через первый ключ с моделями объекта, входы которых соединены через вторые ключи с соответствующими источниками постоянного напряжения, а выходы через блоки вычисления критерия оптимальности соединены с логическим блоком, выход которого соединен с объектом н блок синхронизации, соединенные первым и вторым ключами (2J. К недостаткам известного регулятора относится его малая точность. Целью изобретения является увеличение точности регулятора путем использования данного устройства при синтезе систем, оптимизируемых по критерию качества, представляющему собой интеграл за время переходного процесса, например при оптимизации по быстродействию. Поставленная цель достигается тем, что квазиоптимальный регулятор содержит третий ключ, вход каждой модели объекта соединен через третий ключ с выходом модели регулятора, один вход которогосоединен с выходом модели объекта, второй вход соединен с задатчиком вь1ходной величины объекта, а одни из выходов блока синхронизации соединен с одним нз входов третьего ключа. На чертеже изображен квазиоптимальиый регулятор. Регулятор состоит из объекта регулирования 1, блока задания начальных условий 2, модели объекта 3, модели регулятора 4, блока 5 вычисления критерия оптимальности, логического блока б, выбирающего из ряда функционалов минимальный и задающий на Объект регулирования значение управляющего воздействия, обеспечивающего модели минимум функционала, блока синхронизации 7, источника постоянного напряжения 8первого, второго и третьего ключей 9, 10, П, задатчика выходной величины объекта 12. Ц , Ц ,...UT - фиксированные значения управляющего воздействия (варианты управления), Хм - желаемое значение выходной величины. К) , Ка, Ki - группы ключей, управляющих работой схемы. Работа схемы происходит следующим об разом. В начальный момент времени ключ 9 замкнут, остальные -ключи разомкнуты, тем самым осуществляется задание начальных условий в модель объекта 3. После заданий начальных условий в модель объекта 3, ключи 9 и 11 разомкнуты, а ключи 10 замкнуты. На каждую из моделей 3 объекта поступает одно из фиксированных значений управляющего воздействия (вариант управления), модель переходит в режим peuieния и прогнозирует на время прогноза значения фазовых координат объекта. После конца прогноза ключи 11 замыкаются, остальные разомкнуты, вход модели объекта 3 замыкается с выходом через модель регулятора 4 на другой вход которого поступает желаемое значение выходной величины. Все это время, начиная с начала прогноза до конца переходного процесса в модели объекта 3, замкнутой моделью регулятора 4, блоки вычисления критерия оптимальности 5 вырабатывают значения функционала от фазовых координат. Этим функциoнaлo 4 .может быть, например время от начала прогноза до момента, когда ошибка между желаемым и текущим значением выходной величины на модели не превыщает 6./. е. „.рвона,аль,о« величины. П .. окончания переходного процесса в последней из моделей объекта 3, логический блок 6 сравнивает зиачения функционалов и задает на объект 1 значение управляющего воздействия той модели объекта 3, величина функционала на выходе блока вычисления критерия оптимальности которой была минимальной. После этого цикл повторяется. Рассмотрим в качестве примера функционал минимума среднеквадратичной ощибки. Представим его в виде суммы двух слагаемых:., -minS (х-тХж) dt . min S(x--x«)2dt-1+ §(х-х„)М1 Минимизация функционала происходит по управляющему воздействию, то есть выбирается такое значение управляющего воздействия, которое доставляло бы минимум функционалу. Управляющее воздействие, доставляющее минимум одному из слагаемых, совсем не обязательно обеспечивает минимум всей сумме, поскольку при этом значение второго слагаемог9 может быть достаточно велики. Отсюда следует, что система оптимальная в смысле функционала ф (и) (х -x) будет неопт мальма в смысле функционала Ф)и) §(х - х dt. Второе слагаемое в сумме несет в себе информацию о дальнейшем поведении систе-мы и представляет собой интеграл с момента времени з До конца переходного процесса Т от квадрата ошибки системы. Для его определения при решении задачи минимизации функционала необходимо знать как функцию времени, так и управляющее воздействие, которое, начиная с момента вреMeHHtj , сводит ошибку системы к нуйю оптимальным образом. В .предлагаемом устройстве наилучшее управление выбирается из предположения, что, начиная с момента времениt, система управляется с помощью известного регулятора, что дает возможность учесть измене нйе второго слагаемого в сумме в зависимости от выбранного варианта управляющего воздействия. В качестве модели объекта и модели регулятора могут использоваться цепи, собранные на RC-цепочках и операционных усилителях. В качестве модели регулятора может использоваться любой известный регулятор, например, пропорциональный. Един- . ствённым требованием к нему является устойчивость модели объекта 3, замкнутоймоделью регулятора 4. Модель регулятора 4 следует синтезировать такой, чтобы параметры ее, при выбранной структуре регулятора, обеспечивали минимум заданного функционала. Блок синхронизации 7 управляет рабо л « й9: „ГГтГь„:ер ±;кнуты, задание начальных условий на модели. Afe - ключ 10 замкнут, остальные разомкнуты, модель в режиме рещеиия; А Ig - ключ 11 замкнут, остальные разом кнуты, модель в режиме решения, в конце интервала после конца переходного процесса происходит анаЛиз полученных функционалов и выдача управляющего воздействия иа объект 1., В простейшем случае блок синхронизации 7 может работать по жесткой программе и состоять из трех последовательно соединенных одновибраторов, выход последнего из которых идет иа запуск первого. В качестве ключей могут применяться реле. В качестве блока вычисления функционала, для задачи минимума среднеквадратичной опгибки например, последовательно соединенные квадратор и интегратор. В качестве модели объекта и модели регулятора могут использоваться цепи, собранные на RC-цепочках и операционных усилителях В качестве модели регулятора может служить любой регулятор, например пропорциональиый. К достоинствам предлагаемого квазиоптимального регулятора следует отнести получение для широкого класса объектов более оптимальных переходных процессов, чем может обеспечить наилучший известный для .данного объекта регулятор. Формула изобретения Квазиоптимальный регулятор, содержащий блок задания начальных условий, соединенный через первый ключ с моделями объекта, входы которых соединены через вторые ключи с соответствующими источниками постоянного напряжения, а выходы через блоки вычисления критерия оптимальности соединены с логическим блоком, выход которого соединен с объектом, и блок синхронизакии, соединенный с первым и вторым ключами, отличающийся тем, что. с целью увеличения точности регулятора, он со дер ж нт третий ключ, вход каждой модели объекта соединен через третий ключ с выходом модели регулятора, один вход которого соединен с выходом модели объекта, а второй вход соединен с задатчиком выходной величины объекта, а один из вь)ходов блонд синхронизации соединен с одним из входов третьего ключа, Источники информации, принятые во внимание при экспертизе . Александровский П. М. Элементы теории оптимальных систем автоматического управления, М., 1969, с. 120. 2. Труды МЭИ вып. 53, М., 1965, с. 82-. 102.

| название | год | авторы | номер документа |
|---|---|---|---|
| Квазиоптимальный регулятор | 1983 |
|
SU1164664A1 |
| Система с переменной структурой | 1978 |
|
SU744453A1 |
| Устройство управления инерционным объектом | 1988 |
|
SU1755262A1 |
| Система экстремального управления для объекта с запаздыванием | 1981 |
|
SU993206A1 |
| Система синергетического стохастического управления технологическим процессом анаэробной очистки сточных вод | 2024 |
|
RU2835756C1 |
| СПОСОБ САМОНАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ ОБЪЕКТОМ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2304298C2 |
| СПОСОБ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ РОТОРА РЕАКТИВНОЙ ГИДРАВЛИЧЕСКОЙ ТУРБИНЫ И ПИД-РЕГУЛЯТОР ЧАСТОТЫ ВРАЩЕНИЯ СИЛЬНОГО ДЕЙСТВИЯ | 2021 |
|
RU2781087C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ В НЕЛИНЕЙНОЙ СИСТЕМЕ И СЛЕДЯЩАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2149437C1 |
| Система идентификации параметров многомерного нелинейного динамического объекта | 1986 |
|
SU1385122A1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ОПТИМАЛЬНОЙ ИМПУЛЬСНОЙ НАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ | 2006 |
|
RU2384872C2 |



Авторы
Даты
1979-02-05—Публикация
1976-06-01—Подача