Изобретение относится к системам управления с ограничением по управлению. Этими ограничениями (по положению, скорости, ускорению и т.д.) обладают все практически встречающиеся системы управления. Когда управление по какой-либо из упомянутых составляющих превышает допустимый уровень - уровень ограничения, система может стать неустойчивой ввиду неэффективности ограниченного управления.
Целью изобретения является повышение точности и устойчивости системы.
Достигается это тем, что алгоритм адаптации параметров синтезирован на основе второго метода Ляпунова и действует только тогда, когда система уже не эффективна и может потерять без настройки параметра в цепи обратной связи устойчивость;
Рассматривают задачу обеспечения устойчивости системы управления в случае, когда сигнал управления ограничен. На практике такая ситуация имеет место при наличии в системе управления элементов с насыщением.
Пусть объект управления описывается дифференциальным уравнением вида (для упрощения рассуждений первого порядка) = a(t)X +b(t)U1 (1) а регулятор формирует U1(t) по алгоритму
= a(t)X +b(t)U1 (1) а регулятор формирует U1(t) по алгоритму
U1(t) = K(t)Х(t) + m(t)U(t) (2) где а(t), b(t) - переменные параметры объекта;
m(t), k(t) - настраиваемые параметры регулятора.
В общем случае ограничения по фазовым координатам в системе = [a(t) + b(t)k(t)]X +b(t) m(t)U (3) могут быть представлены в виде
= [a(t) + b(t)k(t)]X +b(t) m(t)U (3) могут быть представлены в виде
U1 ≅U1доп (4)
Управление U1(t) cтановится малоэффективным при U1>U1доп, поэтому система управления (3) может стать неустойчивой (Емельянов С.В. Система автоматического управления с переменной структурой. - М.: Наука, 1967, 335 с).
Для этого случая разность ε (t) имеет вид
ε (t) = U1 - U1доп. (5)
Если ε _→ 0 , то система (3) работает в линейном режиме. Компенсировать ошибку ε (t) можно путем создания сигнала перестройки
εн=Δk(t)X+Δm(t)U (6)
В cигнале настройки (6) подстраивают параметры k(t) и m(t), чтобы выполнялось равенство
ε (t) - ε н(t) = 0. (7)
С этой целью необходимо синтезировать алгоритмы адаптации параметров k(t) и m(t), для чего выбирают функцию Ляпунова
V=κoεεн+[Δkтр2+Δmтр2]˙0,5 (8)
Находят производную функцию Ляпунова по времени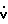 = κo(
= κo( +
+ 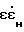 ) + Δk
) + Δk
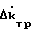 + Δm
+ Δm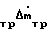 (9)
(9)
Определяют значение 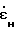 из выражения (6):
из выражения (6):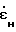 =
=  U + Δm
U + Δm +
+  X + Δk
X + Δk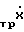 (10)
(10)
подставляют его в выражение (9) и получают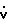 =
=  (ΔmтрU + ΔkтрX)+ κo(
(ΔmтрU + ΔkтрX)+ κo(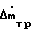 U + Δm
U + Δm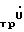
+ 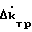 X + Δk
X + Δk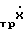 ) + Δk
) + Δk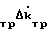 + Δm
+ Δm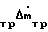 (11) Переписывают выражения (11) в эквивалентном виде;
(11) Переписывают выражения (11) в эквивалентном виде; = κoΔkтр
= κoΔkтр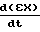 + κoΔmтр
+ κoΔmтр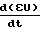 +
+ 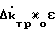 X
X
+  U + Δk
U + Δk + Δm
+ Δm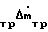 (12)
(12)
Полагают, что выполняются равенства для Δ kтр (для Δ mтраналогично):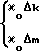
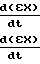


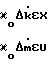

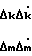

 (13) тогда из выражения (12) значение
(13) тогда из выражения (12) значение = -κ
= -κ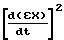 +
+ 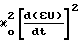 b(t)≅ 0; b(t)> 0 (14) если положить одновременное выполнение равенств
b(t)≅ 0; b(t)> 0 (14) если положить одновременное выполнение равенств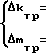
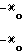

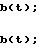

 (15)
(15)
Из равенств (15) можно окончательно записать алгоритмы адаптации параметров k(t) и m(t) в приращениях соответственно Δk(t) и Δm(t):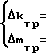
 (16)
(16)
Алгоритм адаптации параметров k(t) и m(t) получен с использованием покомпонентного формирования, в данном случае пропорциональной и дифференциальной составляющих, этого алгоритма.
Этот метод позволяет получить практически все известные составляющие в контуре адаптации из условия гарантированного обеспечения устойчивости процедур адаптации. Показывают это на примере формирования релейной, степенной и интегральной составляющих.
Представляют первую строку из равенств (13) в эквивалентном виде (при b(t) = 1);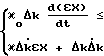
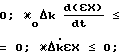
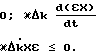

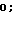 (17)
(17)
Первый столбец из равенств (17) дает возможность получить алгоритм адаптации в виде выражений (16), а из второго и третьего столбцов получают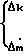

 (18)
(18)
Ввиду того, что для 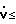 0 необходимо одновременное выполнение равенств (15) и (18), алгоритм адаптации параметров может быть записан в следующем виде:
0 необходимо одновременное выполнение равенств (15) и (18), алгоритм адаптации параметров может быть записан в следующем виде: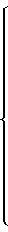
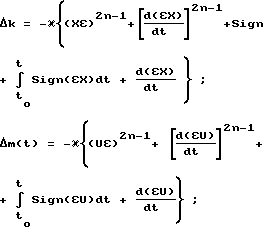
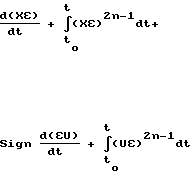

Для упрощения изложения работы системы управления рассмотрим объект управления с обратной связью по положению и настраиваемым входным сигналом.
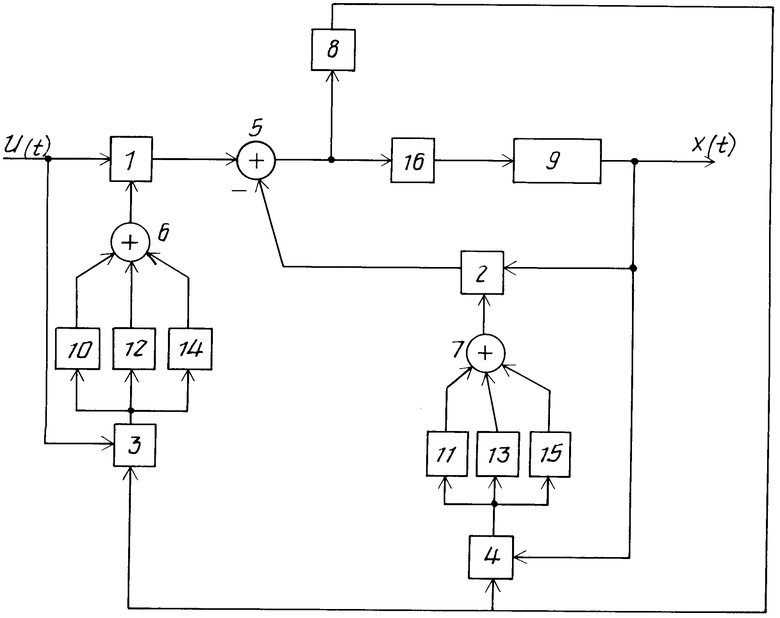
На чертеже представлена функциональная схема адаптивной нелинейной системы управления.
Система содержит блоки 1-4 умножения, сумматоры 5-7, нелинейный блок 8 с зоной нечувствительности, нестационарный объект 9 управления с ограничением по положению, дифференциаторы 10,11, интеграторы 12, 13, усилители 14, 15, регулятор 16.
Работает система следующим образом.
Входной сигнал U(t) через блок 1 умножения поступает на суммирующий вход сумматора 5, на вычитающий вход которого поступает сигнал с выхода блока 2 умножения, на один из входов которого поступает сигнал с выхода объекта 9 управления. На вторые входы блоков 1 и 2 умножения поступают сигналы настройки параметров соответственно m(t) и k(t).
Контур адаптации параметра m(t) cодержит пропорционально-интегрально-дифференциальный регулятор (дифференциатор 10, интегратор 12 и усилитель 14), блок 3 умножения и сумматор 6. Контур адаптации параметра k(t) cодержит аналогичный состав блоков: дифференциатор 11, интегратор 13, усилитель 15, сумматор 7 и блок 4 умножения. Отличие в структуре этих контуров лишь в том, что на вход блока 3 умножения поступает сигнал U(t), а на вход блока 4 умножения - сигнал Х(t). На их вторые входы поступает один и тот же сигнал ε (t).
Настройка параметров m(t) и k(t) производится до тех пор, пока сигнал ε (t) не станет равным нулю. В этом случае сигнал U1(t) ≅U1доп, тем самым запас устойчивости по фазе не увеличивается. В результате параметры m(t) и k(t) подстраиваются таким образом, чтобы сигнал U1(t), поступающий на вход регулятора 16 и далее на вход объекта 9 управления, не превышал сигналов ограничения
U1доп=  U1доп,
U1доп,  доп,
доп,  доп,...,U
доп,...,U . Система управления даже при превышении сигналом управления ограничений U1доп ведет себя как система линейная, а сигнал управления в ней никогда не превышает ограничений.
. Система управления даже при превышении сигналом управления ограничений U1доп ведет себя как система линейная, а сигнал управления в ней никогда не превышает ограничений.
Когда U1(t) ≅ U1доп, ε (t) = 0, k(t) = Ko, m(t) = mo, искажения полезного входного сигнала в линейной зоне системы управления не происходит.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА АДАПТИВНОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМИ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ | 1990 |
|
RU2031434C1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ С ЭТАЛОННОЙ МОДЕЛЬЮ | 1990 |
|
RU2027211C1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ПАРАМЕТРОВ НЕСТАЦИОНАРНОГО ОБЪЕКТА С ПЕРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ | 1990 |
|
RU2027214C1 |
| Система адаптивного управления | 1991 |
|
SU1807446A1 |
| Самонастраивающаяся система управления с эталонной моделью | 1990 |
|
SU1827664A1 |
| СИСТЕМА АДАПТИВНОГО УПРАВЛЕНИЯ САМОЛЕТОМ ПО УГЛУ ТАНГАЖА | 2010 |
|
RU2445671C2 |
| Система управления | 1991 |
|
SU1792539A3 |
| Система идентификации параметров | 1990 |
|
SU1837260A1 |
| Адаптивная система управления | 1991 |
|
SU1807447A1 |
| СИСТЕМА ПРЯМОГО АДАПТИВНОГО УПРАВЛЕНИЯ | 2007 |
|
RU2367991C2 |
Изобретение относится к системам управления с ограничением сигнала управления. Целью изобретения является повышение точности и устойчивости системы управления, которая достигается тем, что система дополнительно содержит нелинейный блок с зоной нечувствительности, второй и третий сумматоры, два усилителя и два дифференциатора. 1 ил.
АДАПТИВНАЯ НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ, содержащая сумматор, входы которого подключены к выходам первого и второго блоков умножения, первый вход первого блока умножения является входом системы и подключен к первому входу третьего блока умножения, соединенного выходом с входом первого интегратора, первый вход второго блока умножения подключен к первому входу четвертого блока умножения, выход которого подключен к входу второго интегратора, а второй вход соединен с вторым входом третьего блока умножения, и объект управления, отличающаяся тем, что в нее введены регулятор, нелинейный блок с зоной нечувствительности, второй и третий сумматоры, два усилителя и два дифференциатора, выход первого сумматора соединен с входом нелинейного блока с зоной нечувствительности и через регулятор соединен с входом объекта управления, выход которого является выходом системы и подключен к второму входу второго блока умножения, выход третьего блока умножения через первый дифференциатор и первый усилитель подключен к первому и второму входам второго сумматора, третий вход которого соединен с выходом первого интегратора, а выход подключен к второму входу первого блока умножения, выход которого через нелинейный блок с зоной нечувствительности соединен с вторым входом четвертого блока умножения, выход которого через второй дифференциатор и второй усилитель подключен к первому и второму входам третьего сумматора, третий вход которого соединен с выходом интегратора, а выход подключен к второму входу второго блока умножения.
| Борцов Ю.А | |||
| и др | |||
| Электро-механические системы с адаптивным и модальным управлением | |||
| Л.: Энергоатомиздат, 1984, с.107, рис.4.3. |
Авторы
Даты
1995-01-20—Публикация
1990-11-19—Подача