СПОСОБ ОПТИЧЕСКОГО ИЗМЕРЕНИЯ ФОРМЫ ПОВЕРХНОСТИ ТРЕХМЕРНОГО ОБЪЕКТА (ВАРИАНТЫ) Российский патент 2004 года по МПК G01B11/25 

Настоящее изобретение относится к топографии, профилометрии, в частности к бесконтактным методам измерений формы поверхности сложных трехмерных объектов с помощью оптического излучения, и может быть использовано в машиностроении, медицине, стоматологии, косметологии, судебно-медицинской экспертизе.

Известен способ оптического измерения формы поверхности трехмерного объекта, описанный в статье Mitsuo Takeda, Kazuhiro Mutoh "Fourier transform profilometry for the automatic measurement of 3-D object shapes", Applied Optics, Vol. 22, №24, pp. 3977-3982, 1983. Способ заключается в том, что на исходный трехмерный объект вдоль одного направления, которое имеет широту θ и долготу ϕ в системе координат (X, Y, Z), связанной с исходным трехмерным объектом, проецируют изображение решетки с заданной пространственной частотой штрихов ω. Штрихи решетки перпендикулярны плоскости, проходящей через указанное направление и ось Z. Формируют изображение объекта в направлении оси Z и регистрируют двухмерное изображение объекта в плоскости, параллельной плоскости (X, Y). Полученное изображение используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта.

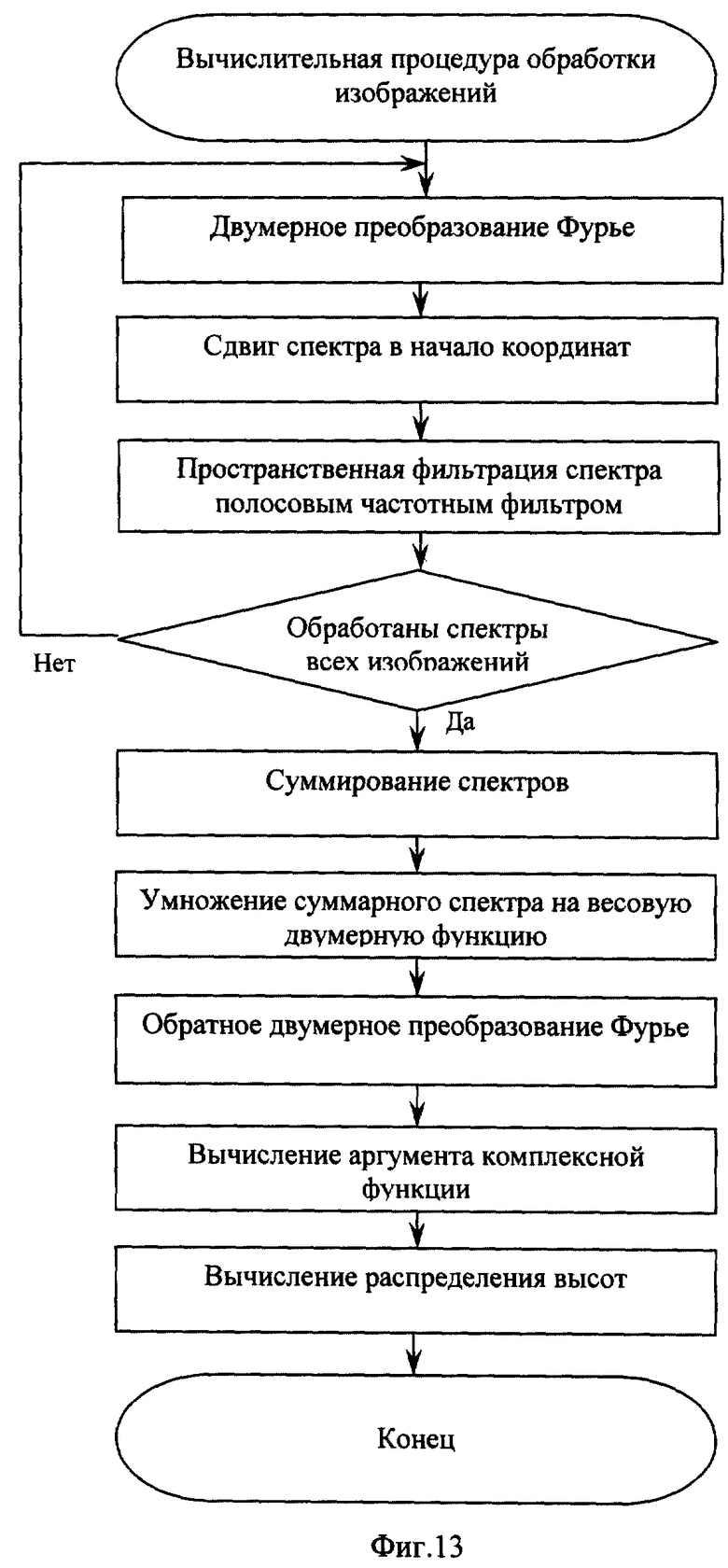
Суть дальнейшего восстановления формы заключается в следующем. Так как направления проецирования штрихов решетки и регистрации изображения не совпадают, то из-за параллакса и кривизны поверхности объекта спроецированные полосы наблюдаются искривленными. Информация о высоте профиля объекта содержится в искривлении полос. Основные этапы вычислительной процедуры обработки полученных изображений и восстановления по ним профиля поверхности следующие:

1. Вычисляют двухмерное преобразование Фурье и получают спектр изображения в спектральной системе координатах (U, V). Так как изображение представляет собой систему спроецированных полос, то пространственный спектр будет иметь ярко выраженные пики (в оптике - порядки дифракции) вблизи пространственных частот, кратных пространственной частоте ω штрихов решетки.

2. Осуществляют сдвиг +1-го (или -1-го) порядка полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов решетки ω, вдоль направления, составляющего с осью U угол, равный долготе ϕ.

3. Выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат, а его ось составляет с осью V угол, равный долготе ϕ.

4. Вычисляют обратное двухмерное преобразование Фурье. В результате получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта.

Основные недостатки известного способа, взятого за прототип, заключаются в неудовлетворительном пространственном разрешении восстановленного изображения в направлении, перпендикулярном направлению штрихов решетки, и снижении точности восстановления объектов с затененными участками. Это вызвано следующим.

Для успешного восстановления формы объекта и повышения точности восстановления профиля поверхности необходимо, чтобы спектр изображения решетки вблизи ±1-го порядков дифракции не перекрывался бы со спектром нулевого порядка. Расстояние между 0-м и ±1-м порядками в частотной области определяется частотой решетки (или периодом полос). Более хорошего разделения порядков дифракции можно добиться путем увеличения этой частоты решетки. Однако пространственная частота не может возрастать до бесконечности. Ее верхний предел ограничен пространственным разрешением оптической и цифровой системы обработки изображений.

Если исследуемый объект имеет сложную поверхность с множеством мелких деталей, то неизбежно будет возникать частичное перекрытие 0-го и ±1-го порядков спектра. Следовательно, при полосовой фильтрации будет происходить потеря информации о высокочастотной части спектра объекта, что и приводит к снижению пространственного разрешения восстановленного изображения в направлении, перпендикулярном направлению штрихов решетки.

Другой недостаток данного способа связан с тем, что на объектах с большой крутизной поверхности при подсветке с одного ракурса возникают обширные затененные участки. На этих же участках поверхности будет также низкая контрастность зарегистрированных полос. Наличие затененных участков не позволяет измерять всю поверхность объекта.

В основу настоящего изобретения положена задача создания способа оптического измерения формы поверхности трехмерного объекта, обеспечивающего за счет многоракурсной подсветки объекта уменьшение областей затенения на объекте, а также минимизацию потерь информации при частотной фильтрации спектра изображения и, соответственно, увеличение пространственного разрешения восстановленного объекта во всех направлениях, что позволяет использовать предлагаемый способ для всех типов объектов при повышении точности измерений.

Поставленная задача решается тем, что в способе оптического измерения формы поверхности трехмерного объекта, заключающемся в том, что на исходный трехмерный объект вдоль одного направления, которое имеет широту θ и долготу ϕ в системе координат (X, Y, Z), связанной с исходным трехмерным объектом, проецируют изображение решетки с заданной пространственной частотой штрихов ω, которые перпендикулярны плоскости, проходящей через указанное направление и ось Z, формируют изображение объекта в направлении оси Z и регистрируют двухмерное изображение объекта в плоскости, параллельной плоскости (X, Y), над полученным изображением объекта выполняют двухмерное преобразование Фурье, в результате которого получают спектр изображения в спектральной системе координат (U, V), осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов решетки ω, вдоль направления, составляющего с осью U угол, равный долготе ϕ, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале спектральной системы координат (U, V), а его ось составляет с осью V угол, равный долготе ϕ, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта, согласно изобретению на исходный трехмерный объект вдоль N дополнительных направлений, имеющих различную долготу ϕ_j, где j=1, 2,...,N, последовательно проецируют изображения j-х решеток с пространственной частотой штрихов ω_j, причем штрихи j-й решетки перпендикулярны плоскости, проходящей через j-e направление и ось Z, дополнительно регистрируют N изображений объекта, над каждым j-м изображением выполняют двухмерное преобразование Фурье и получают спектр j-го изображения, осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов j-й решетки ω_j, вдоль направления, составляющего с осью U угол, равный долготе ϕ_j, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат, а его ось составляет с осью V угол, равный долготе ϕ_j, суммируют полученные спектры от всех изображений, умножают полученный суммарный спектр на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости (U, V) равно числу, обратному количеству просуммированных в этой точке спектров, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта.

Многоракурсная подсветка может быть реализована различными способами:

1) проецирование изображений решеток вдоль дополнительных направлений осуществляют путем вращения вокруг оси Z исходного трехмерного объекта;

2) проецирование изображений решеток вдоль дополнительных направлений осуществляют путем вращения направления проецирования решетки вокруг оси Z.

Поставленная задача решается также тем, что в способе оптического измерения формы поверхности трехмерного объекта, заключающемся в том, что на исходный трехмерный объект вдоль одного выбранного направления, которое имеет широту θ и долготу ϕ в системе координат (X, Y, Z), связанной с исходным трехмерным объектом, проецируют изображение решетки с заданной пространственной частотой штрихов ω, которые перпендикулярны плоскости, проходящей через указанное направление и ось Z, формируют изображение объекта в направлении оси Z и регистрируют двухмерное изображение объекта в плоскости, параллельной плоскости (X, Y), над полученным изображением объекта выполняют двухмерное преобразование Фурье, в результате которого получают спектр изображения в спектральной системе координат (U, V), осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов решетки ω, вдоль направления, составляющего с осью U угол, равный долготе ϕ, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат спектральной системы (U, V), а его ось составляет с осью V угол, равный долготе ϕ, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта, согласно изобретению, на исходный трехмерный объект вдоль N дополнительных направлений, имеющих различную долготу ϕ_j, где j=1, 2,.... N, одновременно проецируют изображения j-х решеток различного цвета с пространственной частотой штрихов ω_j, причем штрихи j-й решетки перпендикулярны плоскости, проходящей через j-e направление и ось Z, при формировании изображения объекта осуществляют пространственное разделение по цвету на N каналов и в каждом канале выполняют регистрацию изображения одного цвета, над каждым j-м изображением выполняют двухмерное преобразование Фурье и получают спектр j-го изображения, осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов j-й решетки ω_j, вдоль направления, составляющего с осью U угол, равный долготе ϕ_j, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат, а его ось составляет с осью V угол, равный долготе ϕ_j, суммируют полученные спектры от всех изображений, умножают полученный суммарный спектр на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости (U, V) равно числу, обратному количеству просуммированных в этой точке спектров, выполняют обратное двухмерное преобразование Фурье и получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта.

Основной технический эффект предлагаемого изобретения заключается в следующем. Многоракурсная подсветка позволяет избежать потери информации при частотной фильтрации Фурье-спектра изображения и, соответственно, избежать уменьшения пространственного разрешения восстановленного объекта. При частотной фильтрации спектров различных изображений объекта, подсвеченного с нескольких ракурсов, происходит частичная потеря информации на различных участках спектральной плоскости. Операция суммирования полученных спектров с последующим умножением на двухмерную весовую функцию (нормирование спектра на единицу) позволяет более полно заполнить частотную плоскость спектральными компонентами исследуемого объекта. В результате можно компенсировать частичную потерю информации в спектре изображения объекта, полученного под одним ракурсом, за счет наличия этой информации в спектрах изображений объекта, полученных под другими ракурсами. Эта процедура похожа на известный в томографии метод реконструкции изображений по проекциям - Фурье-синтез.

За счет многоракурсной подсветки можно восстанавливать форму поверхности трехмерных объектов, имеющих большую крутизну и, соответственно, затененные участки. Наличие затененных участков на объекте при освещении с одного направления компенсируется за счет наличия освещения с других направлений, при которых данные участки объекта не являются затененными.

В дальнейшем предлагаемое изобретение поясняется конкретными примерами его выполнения и прилагаемыми чертежами, на которых:

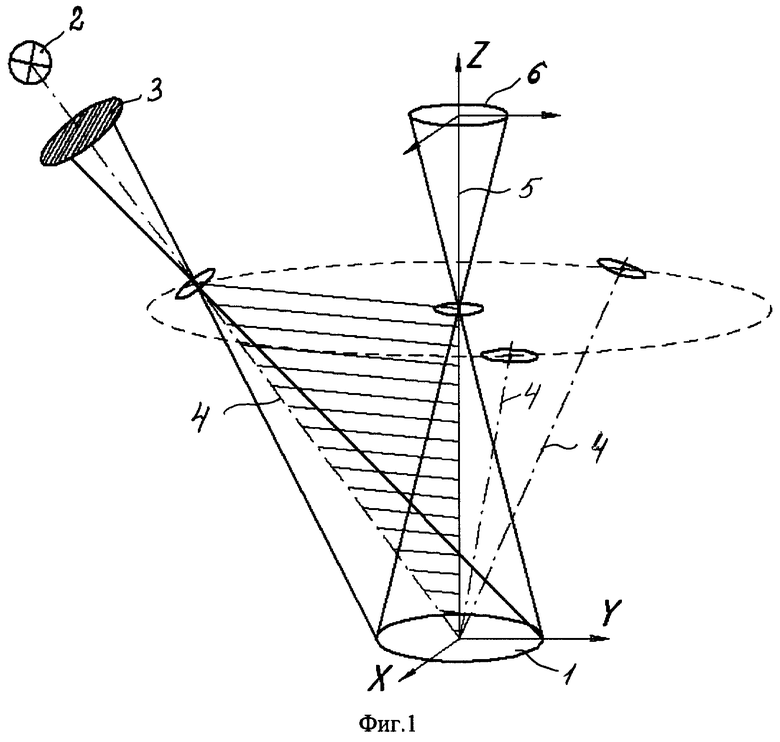
фиг.1 изображает схему многоракурсной подсветки и регистрации изображения объекта;

фиг.2 - пример полутонового изображения исходного трехмерного объекта в виде вложенных один в другой цилиндров;

фиг.3 - пример изображения исходного трехмерного объекта, промодулированного системой полос под одним ракурсом (ϕ_j=0°);

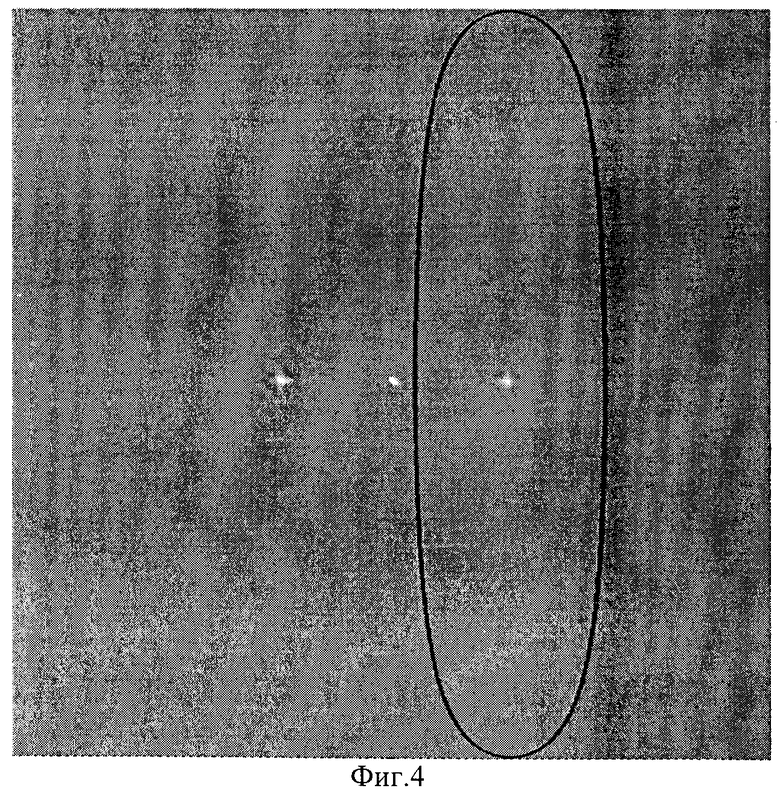
фиг.4 - характерный график двухмерного Фурье-спектра изображения исходного объекта, промодулированного системой полос под одним ракурсом (ϕ_j=0°), и пример изображения границ полосового частотного фильтра;

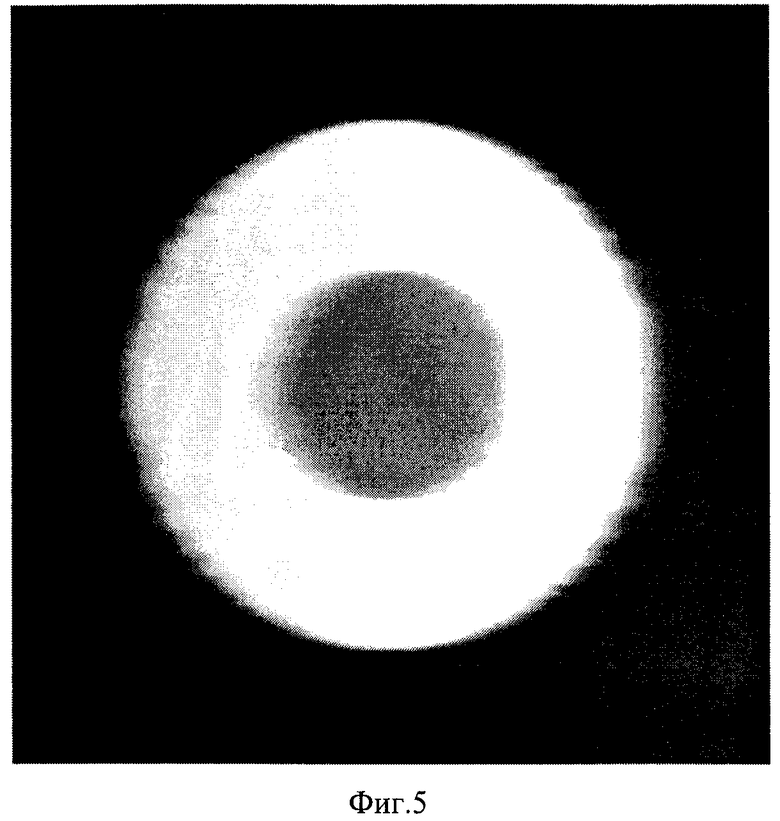
фиг.5 - пример полутонового изображения восстановленного трехмерного объекта при проецировании системы полос под одним ракурсом (ϕ_j=0°);

фиг.6 - пример изображения исходного трехмерного объекта, промодулированного системой полос под одним ракурсом (ϕ_j=90°);

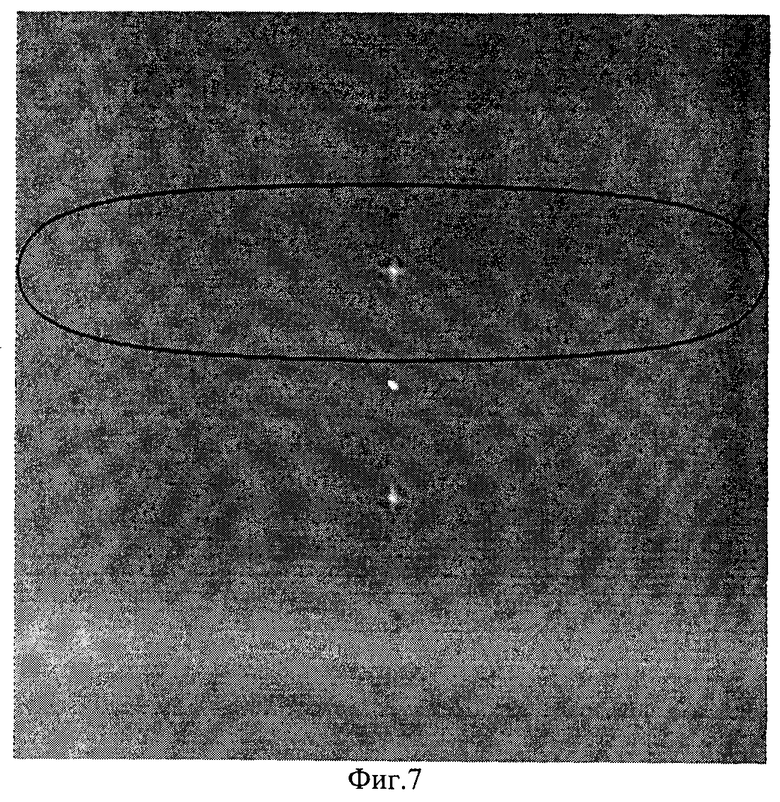
фиг.7 - характерный график двухмерного Фурье-спектра изображения объекта, промодулированного системой полос под одним ракурсом (ϕ_j=90°), и пример изображения границ полосового частотного фильтра;

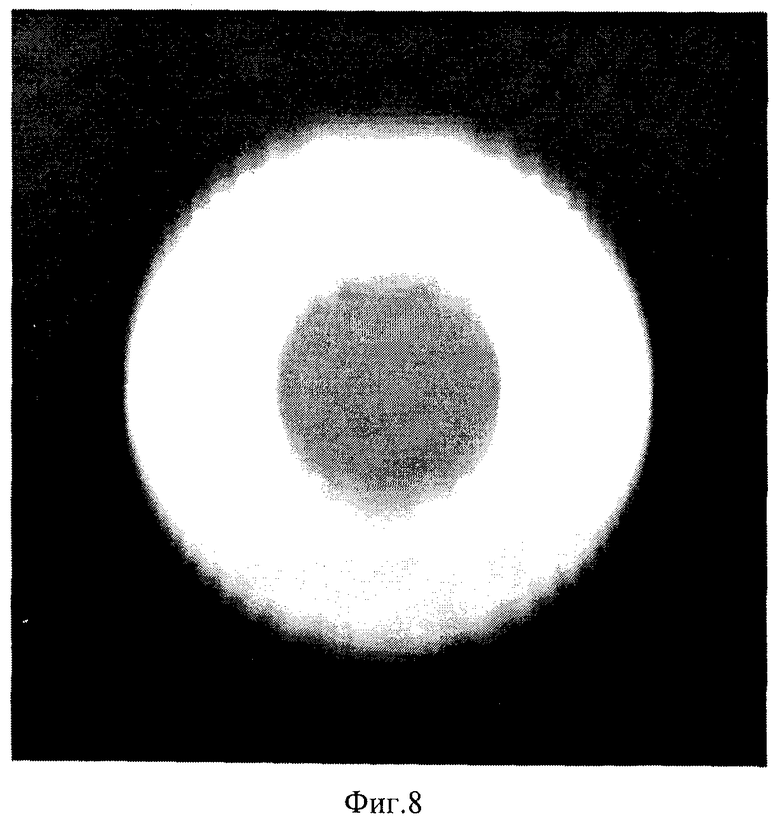
фиг.8 - пример полутонового изображения восстановленного трехмерного объекта при проецировании системы полос под одним ракурсом (ϕ_j=90°);

фиг.9 - график +1-го (-1-го) порядка суммарного Фурье-спектра изображения объекта, промодулированного системой полос под двумя ракурсами (ϕ_j=0° и ϕ_j=90°), и пример изображений границ полосовых частотных фильтров;

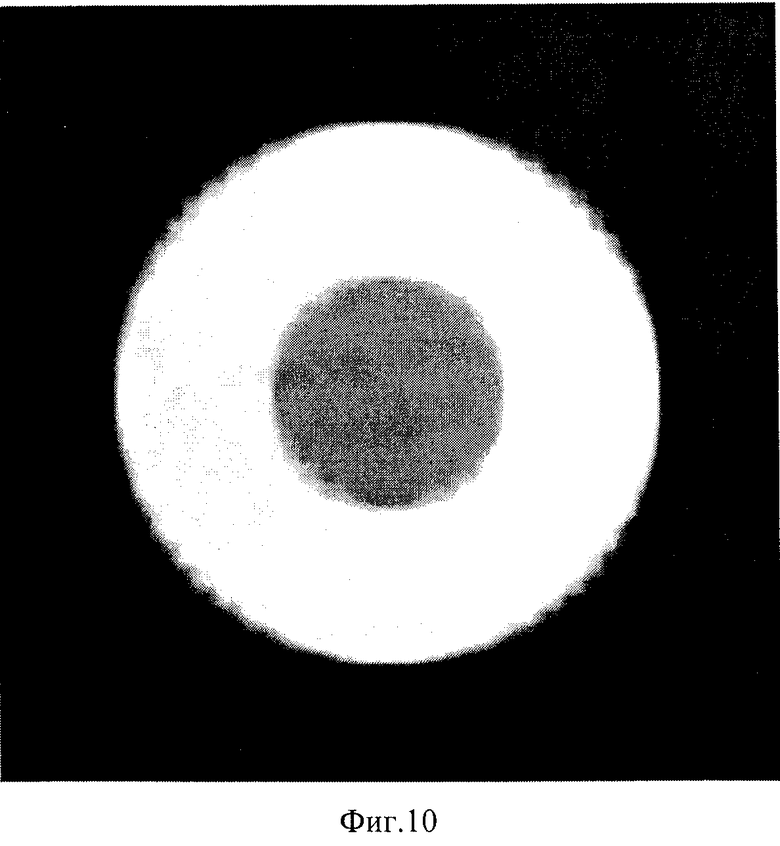
фиг.10 - пример полутонового изображения восстановленного трехмерного объекта при проецировании системы полос под двумя ракурсами (ϕ_j=0° и ϕ_j=90°);

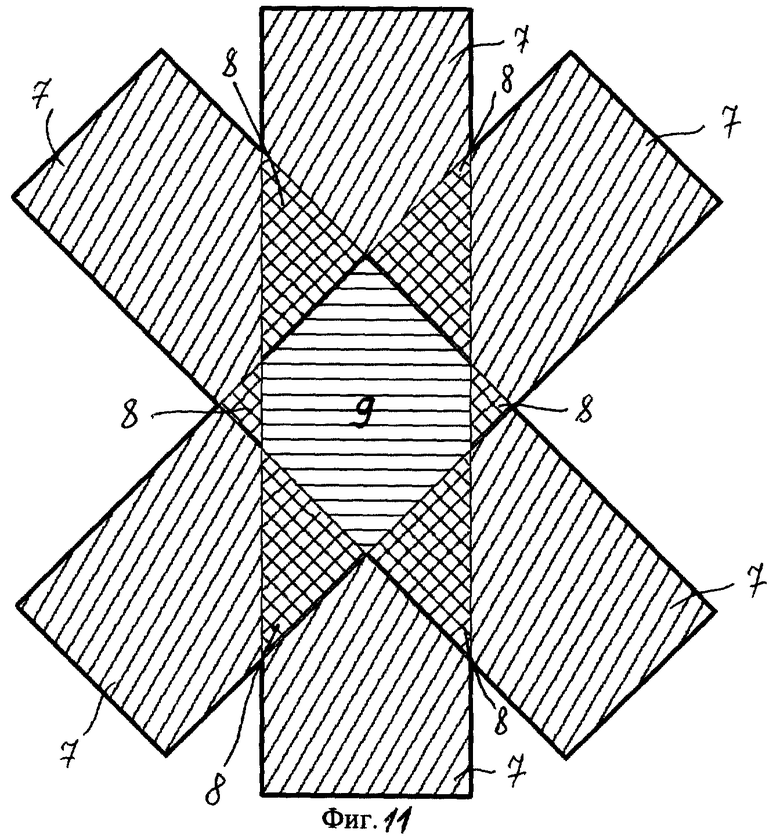
фиг.11 - пример изображения границ двухмерной весовой функции для трехракурсной системы освещения;

фиг.12 - профили исходного объекта и восстановленных объектов при проецировании системы полос под одним и двумя ракурсами;

фиг.13 - блок-схема алгоритма вычислительной процедуры обработки изображений.

Предлагаемый способ оптического измерения формы поверхности трехмерного объекта осуществляют следующим образом. Схема многоракурсной подсветки показана на фиг.1. На исходный трехмерный объект 1, показанный на фиг.2 и представляющий собой вложенные один в другой цилиндры, последовательно проецируют с помощью источника света 2 изображения решеток 3 с заданной пространственной частотой штрихов ω_j вдоль оптических осей 4 освещающих систем по произвольно выбранным N направлениям. Каждое направление имеет широту θ_j и долготу ϕ_j в системе координат (X, Y, Z), связанной с исходным трехмерным объектом 1. Штрихи решетки 3 перпендикулярны плоскости, проходящей через соответствующее направление проецирования и ось Z, в направлении которой формируется изображение и которая является оптической осью 5 отображающей системы. Формируется изображение в плоскости регистратора 6.

Другим вариантом многоракурсной подсветки является одновременное проецирование на поверхность объекта изображений решеток разного цвета. Схема такой многоракурсной подсветки совпадает со схемой подсветки при последовательном проецировании на поверхность объекта изображений решеток и показана на фиг.1. При формировании изображения объекта осуществляют пространственное разделение по цвету на N каналов и в каждом канале выполняют регистрацию изображения одного цвета.

Обработка зарегистрированных N изображений при последовательном проецировании на поверхность объекта изображений решеток и при одновременном проецировании на поверхность объекта изображений решеток разного цвета осуществляется одним методом.

Изображение объекта представляет собой полутоновое изображение объекта, промодулированное пространственным распределением интенсивности освещающего пучка. Для гармонического (синусоидального) закона распределением интенсивности освещающего пучка интенсивность j-го изображения можно описать следующим выражением:

или

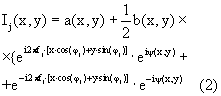
где а - амплитудный фон, b - видность полос, f_j - частота полос, ϕ_j - угол между осью Х и нормалью к направлению полос (долгота направления, вдоль которого проецируются полосы), ψ - искомая функция (фаза), которая связана с формой поверхности. При данной записи пространственное распределение интенсивности освещающего пучка представляет собой полосатую структуру (решетку), штрихи которой ориентированы так, что угол между осью Х и нормалью к направлению полос составляет ϕ_j. Пример такого изображения приведен на фиг.3 и фиг.6 (ϕ_j=0° и ϕ_j=90° соответственно).

Для удобства записи введем следующие обозначения:

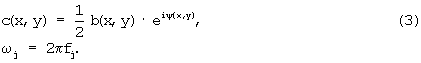
Тогда выражение (2) можно переписать в следующем виде:

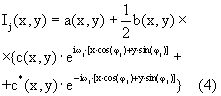
Формируется изображение в направление оси Z, в плоскости, параллельной плоскости объекта.

После регистрации изображений осуществляют вычислительную процедуру обработки полученных данных. Первым этапом данной процедуры является вычисление двухмерного преобразования Фурье и получение спектра изображения в спектральной системе координат (U, V):

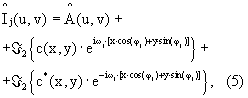
где 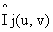- двухмерный Фурье-спектр изображения, ;2 – операция двухмерного преобразования Фурье.

Применяя теорему о сдвиге, спектр изображения можно записать как:

Спектр (6) от системы полос будет иметь ярко выраженные пики вблизи пространственных частот, кратных пространственной частоте ωj штрихов решетки, так называемые +1-й и -1-й порядки спектра (второе и третье слагаемые в выражении (6) соответственно). Первое слагаемое описывает нулевой порядок спектра.

Далее осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину ω_j вдоль направления, составляющего угол ϕ_j с осью U. Эта процедура необходима для перемещения +1-го порядка спектра в начало координат. Математически данная операция представляет собой переход к новой системе координат (U’, V’):

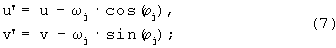
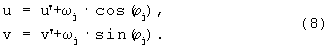
Применяя преобразование координат (8) для выражения (6), получим выражение для спектра, сдвинутого в начало координат:

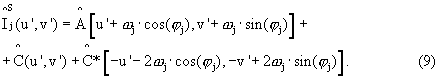
Следующим этапом вычислительной процедуры обработки данных является пространственная фильтрация спектра полосовым частотным фильтром Н с центром в начале координат и осью, составляющей угол (ϕ_j с осью V:

Полосовой фильтр в выражении (10) имеет следующий вид:

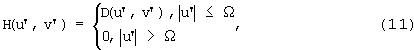
где функция D(u’,v’) либо имеет постоянное значение для прямоугольного фильтра, либо является аподизирующей функцией (например, Хеннинга и т.п.); Ω - ширина фильтра, причем Ω<2·ω.

Таким образом, после частотной фильтрации спектр будет представлять собой +1-й порядок двухмерного Фурье-спектра изображения (1), сдвинутый в начало координат спектральной плоскости (U, V). Пример характерного Фурье-спектра изображения исходного объекта, промодулированного системой полос под одним ракурсом, приведен на фиг.4 и фиг.7 (ϕ_j=0° и ϕ_j=90° соответственно).

Далее суммируют все отфильтрованные спектры

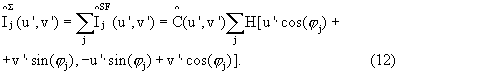
Следует отметить, что ±1-е порядки спектра будут лежать на прямой, проходящей через начало координат спектральной плоскости (U, V) под углом ϕ_j к оси U. Так как расстояние между 0-м и +1-м (-1-м) порядком - величина конечная, которая определяется пространственной частотой ω_j штрихов решетки, то частотная фильтрация приводит к частичной потере информации вдоль прямой, на которой расположены ±1-е порядки спектра. Это вызывает уменьшение пространственного разрешения восстановленного изображения вдоль этого направления. При многоракурсном освещении полосовые частотные фильтры H_j будут иметь различную ориентацию относительно двухмерного Фурье-спектра изображения. Поэтому при фильтрации будут выделяться различные участки спектра. Операция суммирования отфильтрованных спектров позволяет синтезировать спектр исследуемого объекта из различных его участков. В результате повышается пространственное разрешение восстановленного изображения во всех направлениях, так как при сложении потерянные участки одного спектра дополняются за счет других спектров.

При суммировании отфильтрованных спектров на различных участках спектральной плоскости происходит сложение различного количества отфильтрованных спектров, поэтому необходима операция умножения суммарного спектра на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости (U, V) равно числу, обратному количеству просуммированных в этой точке спектров. Смысл такого умножения заключается в том, что на участках спектральной плоскости, где происходит сложение 2, 3,..., N отфильтрованных спектров , значение суммарного спектра надо уменьшить в 2, 3,.... N раз соответственно, чтобы суммарный спектр был отнормирован на единицу. Пример границ двухмерной весовой функции показан на фиг.11. Для наглядности показана весовая функция, которая применяется в процедуре обработки изображений, полученных при трехракурсной системе освещения. В областях, обозначенных цифрой 7, суммарный спектр умножается на 1, так как при суммировании отфильтрованных спектров на этих участках спектральной плоскости не происходит сложение отфильтрованных спектров. В областях под цифрой 8 суммарный спектр умножается на 1/2, так как при суммировании отфильтрованных спектров на этих участках спектральной плоскости происходит сложение двух отфильтрованных спектров. В области под цифрой 9 суммарный спектр умножается на 1/3, так как при суммировании отфильтрованных спектров на этом участке спектральной плоскости происходит сложение трех отфильтрованных спектров.

После операции умножения суммарного спектра на двухмерную весовую функцию получается искомый спектр. Пример такого изображения показан на фиг.9 (для двух ракурсов: (ϕ_j=0° и ϕ_j=90°).

Заключительным этапом процедуры обработки данных является вычисление обратного двухмерного преобразования Фурье и получение двухмерной комплексной функции:

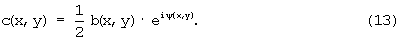
Аргумент ψ(х,у) полученной комплексной функции с(х,у) в выражении (13) связан с формой поверхности исходного трехмерного объекта. Для сравнения на фиг.5, 8 и 10 приведены соответственно примеры полутоновых изображений восстановленных объектов при проецировании полос под одним ракурсом (ϕ_j=0° и ϕ_j=90° соответственно) и при проецировании полос под двумя ракурсами (ϕ_j=0°, (ϕ_j=90°). Профили исходного объекта и восстановленных объектов при проецировании системы полос под одним и двумя ракурсами (кривая 10 - исходный объект, кривая 11 - восстановленный объект при проецировании системы полос под одним ракурсом, кривая 12 - восстановленный объект при проецировании системы полос под двумя ракурсами) показаны на фиг.12.

Блок-схема всего алгоритма вычислительной процедуры обработки изображений показана на фиг.13.

Таким образом, с использованием предложенного способа можно существенно повысить пространственное разрешение восстановленных объектов во всех направлениях и расширить класс исследуемых объектов за счет измерения формы поверхности трехмерных объектов со значительной крутизной и областями затенения.

Метод заключается в проецировании изображений решеток на поверхность объекта с нескольких направлений, регистрации изображений вдоль другого направления и проведении вычислительной процедуры обработки данных, которая заключается в обработке Фурье-спектров зарегистрированных изображений и их суммировании. Суммарный спектр умножают на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости равно числу, обратному количеству просуммированных в этой точке спектров. Выполняют обратное двухмерное преобразование Фурье над обработанным суммарным спектром, результатом которого является изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта. Технический результат – создание способа измерения формы поверхности трехмерного объекта, обеспечивающего за счет многоракурсной подсветки объекта уменьшения области затенения на объект и минимизацию потерь информации при частотной фильтрации спектра изображения. 2 н. и 2 з.п.ф-лы, 13 ил.

1. Способ оптического измерения формы поверхности трехмерного объекта, заключающийся в том, что на исходный трехмерный объект вдоль одного направления, которое имеет широту θ и долготу ϕ в системе координат (X, Y, Z), связанной с исходным трехмерным объектом, проецируют изображение решетки с заданной пространственной частотой штрихов ω, которые перпендикулярны плоскости, проходящей через указанное направление и ось Z, формируют изображение объекта в направлении оси Z и регистрируют двухмерное изображение объекта в плоскости, параллельной плоскости (X, Y), над полученным изображением объекта выполняют двухмерное преобразование Фурье, в результате которого получают спектр изображения в спектральной системе координат (U, V), осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов решетки ω, вдоль направления, составляющего с осью U угол, равный долготе ϕ, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат спектральной системы (U, V), а его ось составляет с осью V угол, равный долготе ϕ, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта, отличающийся тем, что на исходный трехмерный объект вдоль N дополнительных направлений, имеющих различную долготу ϕ_j, где j=1, 2, .... N, последовательно проецируют изображения j-х решеток с пространственной частотой штрихов ω_j, причем штрихи j-й решетки перпендикулярны плоскости, проходящей через j-e направление и ось Z, дополнительно регистрируют N изображений объекта, над каждым j-м изображением выполняют двухмерное преобразование Фурье и получают спектр j-го изображения, осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов j-й решетки ω_j, вдоль направления, составляющего с осью U угол, равный долготе ϕ_j, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат, а его ось составляет с осью V угол, равный долготе ϕ_j, суммируют полученные спектры от всех изображений, умножают полученный суммарный спектр на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости (U, V) равно числу, обратному количеству просуммированных в этой точке спектров, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта.2. Способ по п.1, отличающийся тем, что проецирование изображений решеток вдоль дополнительных направлений осуществляют путем вращения вокруг оси Z исходного трехмерного объекта.3. Способ по п.1, отличающийся тем, что проецирование изображений решеток вдоль дополнительных направлений осуществляют путем вращения направления проецирования решетки вокруг оси Z.4. Способ оптического измерения формы поверхности трехмерного объекта, заключающийся в том, что на исходный трехмерный объект вдоль одного выбранного направления, которое имеет широту θ и долготу ϕ в системе координат (X, Y, Z), связанной с исходным трехмерным объектом, проецируют изображение решетки с заданной пространственной частотой штрихов ω, которые перпендикулярны плоскости, проходящей через указанное направление и ось Z, формируют изображение объекта в направлении оси Z и регистрируют двухмерное изображение объекта в плоскости, параллельной плоскости (X, Y), над полученным изображением объекта выполняют двухмерное преобразование Фурье, в результате которого получают спектр изображения в спектральной системе координат (U, V), осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов решетки ω, вдоль направления, составляющего с осью U угол, равный долготе ϕ, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат спектральной системы (U, V), а его ось составляет с осью V угол, равный долготе ϕ, выполняют обратное двухмерное преобразование Фурье, в результате которого получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта и которые используют для дальнейшего восстановления формы поверхности исходного трехмерного объекта, отличающийся тем, что на исходный трехмерный объект вдоль N дополнительных направлений, имеющих различную долготу ϕ_j, где j=1, 2,..., N, одновременно проецируют изображения j-х решеток различного цвета с пространственной частотой штрихов ω_j, причем штрихи j-й решетки перпендикулярны плоскости, проходящей через j-e направление и ось Z, при формировании изображения объекта осуществляют пространственное разделение по цвету на N каналов и в каждом канале выполняют регистрацию изображения одного цвета, над каждым j-м изображением выполняют двухмерное преобразование Фурье и получают спектр j-го изображения, осуществляют сдвиг полученного спектра в начало координат спектральной плоскости (U, V) на величину, равную пространственной частоте штрихов j-й решетки ω_j, вдоль направления, составляющего с осью U угол, равный долготе ϕ_j, выполняют пространственную фильтрацию спектра полосовым фильтром, центр которого лежит в начале координат, а его ось составляет с осью V угол, равный долготе ϕ_j, суммируют полученные спектры от всех изображений, умножают полученный суммарный спектр на двухмерную весовую функцию, значение которой в каждой точке спектральной плоскости (U, V) равно числу, обратному количеству просуммированных в этой точке спектров, выполняют обратное двухмерное преобразование Фурье и получают изображение, представляющее совокупность комплексных чисел, аргументы которых связаны с искомой формой поверхности исходного трехмерного объекта.