Изобретение относится к способам численного решения системы дифференциальных уравнений, имеющей вид
dYj/dX=Fj(Y1, Y2,... Yn, X), (j=1, 2,..., n), (1)
где X - аргумент; Y1(X), Y2(X),...,Yn(X) - интегралы системы уравнений (1); dYj/dX - производная соответствующего интеграла; Fj(Y1, Y2,..., Yn, X) - заданные функции, и может использоваться для количественного анализа с использованием вычислителя описываемых системами дифференциальных уравнений процессов в природных и технических системах.
Известен способ численного решения системы дифференциальных уравнений [1], который состоит в том, что предварительно задают начальное Хо и конечное Хк значения аргумента, ограничивающие интервал его значений, в котором будут решать систему этих уравнений, разбивают этот интервал на Q участков и задают длину дХi (i=1, 2,..., Q) каждого участка так, чтобы сумма dXi была равна этому интервалу, задают начальные значения Yj(Xo) (j=1, 2,..., n) интегралов системы этих уравнений, в вычислитель устанавливают блок формирования значений аргумента и интегралов в начале каждого участка (БФ), блок вычисления приращений интегралов на каждом участке (БВП), блок вычисления значений интегралов в конце каждого участка (БВИ) и блок вычисления значения аргумента в конце каждого участка и сравнения этого значения с заданным значением Хк (БАС), а в память вычислителя вводят значения Хо, Хк, дХi и Yj(Xoi). В начале решения системы этих уравнений из памяти вычислителя значения Хо и Yj(Xo) подают в БФ, а значения dXi подают в БВП и БАС. При решении системы этих уравнений на каждом i-том участке в БФ формируют значение Xoi аргумента в начале этого участка равным значению Хк(i-1) аргумента в конце предыдущего участка и значения Yj(Xoi) интегралов в начале этого участка равными значениям Yj(XK(i-1)) этих интегралов в конце предыдущего участка, после чего с выхода БФ значение Xoi подают на входы БПВ и БАС, а значения Yj(Xoi) подают на входы БВП и БВИ. В БВП вычисляют значение Fji правой части каждого дифференциального уравнения в начале этого участка при полученных значениях Xoi, Yj(Xoi) и значение приращения дYji каждого интеграла на этом участке как произведение Fji и дХi. С выхода БВП значения дYji подают в БВИ, где вычисляют значения Yj(Xкi) интегралов в конце этого участка как суммы значений Yj(Xoi) и дYji. С выхода БВИ значения Yj(Xкi) подают в память вычислителя и в БФ. В БАС вычисляют значение Хкi аргумента в конце этого участка как сумму значения Xoi и дХi, и с выхода БАС значение Хкi подают в память вычислителя и в БФ. Кроме того, в БАС сравнивают значение Хкi с Хк. Если Хкi < Хк, то переходят в БФ и продолжают вычисления на следующем участке, а если Хкi=Хк, то прекращают вычисления, из памяти вычислителя подают значения Yj(Xкi) (j=1, 2,..., n; i=1, 2,..., Q) в устройство вывода и демонстрируют эти значения на экране дисплея и (или) печатают их на принтере. Недостатком этого способа является невысокая точность полученного приближенного решения системы дифференциальных уравнений, обусловленная тем, что на каждом участке изменения аргумента значения правых частей дифференциальных уравнений принимают постоянными, равными их значениям в начале этого участка, хотя, как правило, эти правые части на этом участке изменяются.
Известен также способ численного решения системы дифференциальных уравнений [2], который состоит в том, что предварительно задают начальное Хо и конечное Хк значения аргумента, ограничивающие интервал его значений, в котором будут решать систему этих уравнений, разбивают этот интервал на Q участков и задают длину дХi (1=1, 2,..., Q.) каждого участка так, чтобы сумма dXi была равна этому интервалу, задают начальные значения Yj(Xo) (j=1, 2,..., n) интегралов системы этих уравнений, в вычислитель устанавливают блок формирования значений аргумента и интегралов в начале каждого участка (БФ), блок вычисления приращений интегралов на каждом участке (БВП), блок вычисления значений интегралов в конце каждого участка (БВИ) и блок вычисления значения аргумента в конце каждого участка и сравнения этого значения с заданным значением Хк (БАС), а в память вычислителя вводят значения Хо, Хк, дХi и Yj(Xoi). Кроме того, предварительно каждый участок разбивают на W подучастков равной длины дХim=дХi/(m=1, 2,..., W), для каждого подучастка задают значение Am весового коэффициента и вводят значения W и Am в память вычислителя. В начале решения системы этих уравнений из памяти вычислителя значения Хо и Yj(Xo) подают в БФ, значения dXi подают в БВП и БАС, а значения W и Am подают в БВП. При решении системы этих уравнений на каждом 1-том участке в БФ формируют: значение Xoi аргумента в начале этого участка, равное значению Хк(i-1) аргумента в конце предыдущего участка; значения интегралов Yj(Xoi) в начале этого участка, равные значениям Yj(Xк(i-1)) этих интегралов в конце предыдущего участка. После этого с выхода БФ значение Xoi подают на входы БПВ и БАС, а значения Yj(Xoi) подают на входы БВП и БВИ. В БВП вычисляют значение длины дХim каждого подучастка и значение Хкim (m=1, 2,...,W) аргумента в конце каждого подучастка как сумму значения Xoim аргумента в начале этого подучастка и дХim, причем значение Xoim принимают равным значению аргумента в конце предыдущего подучастка. В БВП вычисляют также: значение Fji0 правой части каждого дифференциального уравнения в начале этого участка при известных значениях Xoi и Yj(Xoi); значение дYji0 приращения каждого интеграла на этом участке, умножая Fji0 на дХi; значение Fjim правой части каждого дифференциального уравнения в конце каждого подучастка этого участка с использованием значений Хкim, Yj(Xoi) и значений дYji(m-1) приращений интегралов на этом участке, полученных при значениях Fji(m-1); значение дYjim приращения каждого интеграла на этом участке, умножая Fjim на дХi. Затем в ВВП с использованием значений дYjiO, дYjim и Am вычисляют осредненное по всем подучасткам значение дYjiс приращения каждого интеграла на этом участке и с выхода БВП подают значения дUjiс в БВИ, где вычисляют значения Yj(XKi) интегралов в конце этого участка, суммируя соответствующие значения Yj(Xoi) и дYjiс. С выхода БВИ значения Yj(Xкi) подают в память вычислителя и в БФ. В БАС вычисляют значение Хкi аргумента в конце этого участка, суммируя значения Xoi и дХi, и с выхода БАС значение Хкi подают в память вычислителя и в БФ. Кроме того, в БАС сравнивают значение Хкi с Хк. Если Хкi<Хк, то переходят в БФ и продолжают вычисления на следующем участке, а если Хкi=Хк, то прекращают вычисления, из памяти вычислителя подают значения Yj(XKi) (j=1, 2,..., n; 1=1, 2,..., Q) в устройство вывода и демонстрируют эти значения на экране дисплея и (или) печатают их на принтере. Недостатком этого способа является высокая стоимость материальных затрат, потребных для получения достаточно точного решения системы дифференциальных уравнений, что обусловлено большим объемом вычислений, который необходимо при этом выполнять, что требует большого времени работы вычислителя, которое является дорогостоящим.
Прототипом заявляемого изобретения следует считать способ численного решения системы дифференциальных уравнений [2], общими признаками которого с заявляемым изобретением является то, что предварительно задают начальное Хо и конечное Хк значения аргумента, ограничивающие интервал его значений, в котором будут решать систему этих уравнений, разбивают этот интервал на Q участков и задают длину дХi (1=1, 2,..., Q) каждого участка так, чтобы сумма dXi была равна этому интервалу, задают начальные значения Yj(Xo) (j=1, 2,..., n) интегралов системы этих уравнений, в вычислитель устанавливают блок формирования значений аргумента и интегралов в начале каждого участка (БФ), блок вычисления приращений интегралов на каждом участке (БВП), блок вычисления значений интегралов в конце каждого участка (БВИ) и блок вычисления значения аргумента в конце каждого участка и сравнения этого значения с заданным значением Хк (БАС), а в память вычислителя вводят значения Хо, Хк, дХi и Yj(Xoi). В начале решения системы этих уравнений из памяти вычислителя значения Хо и Yj(Xo) подают в БФ и значения dXi подают в БВП и БАС. При решении системы этих уравнений на каждом i-том участке в БФ формируют: значение Xoi аргумента в начале этого участка, равное значению Хк(i-1) аргумента в конце предыдущего участка; значения Yj(Xoi) интегралов в начале этого участка, равные значениям Yj(Xк(i-1)) этих интегралов в конце предыдущего участка. После этого с выхода БФ значение Xoi подают на входы БПВ и БАС, а значения Yj(Xoi) подают на входы БВП и БВИ. В БВП вычисляют значение приращения каждого интеграла на этом участке и с выхода БВП подают эти приращения в БВИ, где вычисляют значения Yj(Xкi) интегралов в конце этого участка, суммируя каждое значение Yj(Xoi) с значением соответствующего приращения. Значения Yj(Xкi) с выхода БВИ подают в память вычислителя и в БФ. В БАС вычисляют значение Хкi аргумента в конце этого участка, суммируя значения Xoi и дХi, и с выхода БАС значение Хкi подают в память вычислителя и в БФ. Кроме того, в БАС сравнивают значение Хкi с Хк. Если Хкi<Хк, то переходят в БФ и продолжают вычисления на следующем участке, а если Хкi=Хк, то прекращают вычисления, из памяти вычислителя подают значения Yj(Xкi) (j=1, 2,..., n; i=1, 2,..., Q) в устройство вывода и демонстрируют эти значения на экране дисплея и (или) печатают их на принтере.
Кроме того, в прототипе предварительно каждый участок разбивают на W подучастков равной длины дХim=дХi/W (m=1, 2,..., W), для каждого подучастка задают значение Am весового коэффициента, вводят значения W и Am в память вычислителя, а в начале решения системы этих уравнений из памяти вычислителя значения W и Am подают в БВП. При решении системы этих уравнений на каждом участке в БВП вычисляют значение длины дХim каждого подучастка и значение Хкim (m=1, 2,..., W) аргумента в конце каждого подучастка, суммируя значение Xoim аргумента в начале этого подучастка и дХim, причем Xoim принимают равным значению аргумента в конце предыдущего подучастка. В БВП вычисляют также: значение Fji0 правой части каждого дифференциального уравнения в начале этого участка при известных значениях Xoi и Yj(Xoi); значение дYji0 приращения каждого интеграла на этом участке, умножая Fji0 на дХi; значение Fjim правой части каждого дифференциального уравнения в конце каждого подучастка этого участка с использованием значений Хкim, Yj(Xoi) и значений дYji(m-1) приращений интегралов на этом участке, полученных при значениях Fji(m-1); значение дYjim приращения каждого интеграла на этом участке, умножая Fjim на дХi. Затем в БВП с использованием значений дYji0, дYjim и Am вычисляют осредненное по всем подучасткам значение дYjiс приращения каждого интеграла на этом участке и с выхода БВП подают значения дYjiс в БВИ.
Недостатком этого способа является высокая стоимость материальных затрат, потребных для получения достаточно точного численного решения системы дифференциальных уравнений, обусловленная большим объемом вычислений, который необходимо при этом выполнять, что требует большого времени работы вычислителя (В), которое является дорогостоящим. Это объясняется тем, что стоимость Сз материальных затрат на численное решение системы дифференциальных уравнений с использованием В возрастает с увеличением времени Тр работы В, которое потребно для решения этой задачи. Допустим, что
Cз=Кз·Тр, (2)
где Кз - коэффициент затрат, величина которого зависит от стоимости амортизации В, оплаты труда обслуживающего В персонала и стоимости затрачиваемой на работу В электроэнергии. Значение Тр прямо пропорционально количеству операций V, которое нужно выполнить в В при решении задачи, и обратно пропорционально производительности L В, которая определяется количеством вычислительных операций (ВО), выполняемых В в единицу времени,
Тр=V/L. (3)
В свою очередь,
V=Vу·Q (4)
где Q - количество участков, на которые разбивают заданный интервал Хк-Хо изменения аргумента при численном решении системы дифференциальных уравнений; Vу - количество ВО, выполняемых на одном участке. В прототипе
Vy=W·Vп+Vд, (5)
где W - количество подучастков, на которые разбивают каждый участок изменения аргумента; Vn - количество ВО, выполняемых на одном подучастке; Vд - количество ВО, выполняемых на каждом участке. При допущении об одинаковой длине дХп всех участков величина Q определяется формулой
Q=(Xк-Хо)/дХп. (6)
Подставим (6) в выражение (4), а полученное выражение подставим в (3). Тогда с учетом (2) получим следующую формулу
Сз=Кз·(Хк-Хо)·Vy/(дХп·L). (7)
Выражение (7) показывает, что стоимость Сз материальных затрат на численное решение системы дифференциальных уравнений возрастает с увеличением заданного интервала Хк-Хо изменения аргумента и с уменьшением длины дХп участка. Покажем, что в прототипе для получения достаточно точного решения системы дифференциальных уравнений необходимо использовать участки малой длины дХп. На каждом из рассматриваемых участков в прототипе закон изменения Yji(X) каждого интеграла принимают в виде линейной функции
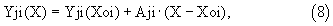
где
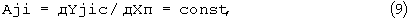
Xoi<X<(Xoi+дХп).
Однако, как правило, функция Yji(X) может существенно отличаться от линейной зависимости (8), причем это отличие возрастает с увеличением длины дХп этого участка. Справедливость этого иллюстрируется следующим расчетом. Пусть закон изменения интеграла Yji(X) на рассматриваемом участке изменения аргумента X, который в прототипе вычисляют по формуле (8), реально имеет вид квадратной параболы
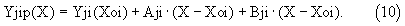
Найдем ошибку Пу значения этого интеграла в конце рассматриваемого участка длиной дХп, полученного по формуле (9), относительно точного значения этого интеграла, определяемого в соответствии с формулой (10),
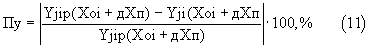
Результаты расчетов зависимости Пу(дХi) (11) для заданных значений коэффициентов Aji=0,5; Bji=0,3 и заданных значений дХп приведены в таблице 1.

Анализ результатов, приведенных в таблице 1, показывает, что если считать достаточно точным решение, при котором ошибка Пу на рассматриваемом участке не превышает 0,1%, то при использовании прототипа необходимо задавать малые (порядка 0,001) значения длины дХп участка, что при большом значении заданного интервала Хк-Хо изменения аргумента обуславливает большую стоимость Сз (7) материальных затрат на получение этого решения с достаточной точностью.
Целью заявляемого изобретения является устранение указанного недостатка прототипа, а именно снижение стоимости материальных затрат, потребных для получения достаточно точного решения системы дифференциальных уравнений, за счет уменьшения объема выполняемых вычислений вследствие увеличения длины участков, на которые разбивают заданный интервал изменения аргумента.
Для достижения этой цели в заявляемом изобретении предварительно множество Yj(X) (j=1, 2,..., n) интегралов заданной системы дифференциальных уравнений делят на две группы, первая из которых содержит интегралы Yp(X) (р=1, 2,..., s), где s<n, называемые "ключевыми", задание закона изменения каждого из которых на каждом участке изменения аргумента в виде соответствующей линейной функции позволяет получить аналитическое решение каждого дифференциального уравнения этой системы на этом участке, а вторая группа содержит остальные интегралы Yv(X) (v=s+1, s+2, ..., n) этой системы уравнений, на каждом участке изменения аргумента закон изменения каждого из "ключевых" интегралов задают соответствующей линейной функцией Yрiл(х) текущего значения х приращения аргумента на этом участке, зависящей от неизвестного значения дYрi приращения этого интеграла на этом участке, значения Ypi(Xoi) этого интеграла в начале этого участка и длины дХi этого участка, с использованием функций Yрiл(х) получают аналитические решения дифференциальных уравнений этой системы, преобразуя которые, получают полиномы дYvi(х), дYрi(х) не ниже второй степени, определяющие изменение приращений соответствующих интегралов на этом участке, и систему алгебраических уравнений относительно значений дYрi, разрабатывают алгоритм решения этой системы алгебраических уравнений известными методами и устанавливают в вычислитель дополнительно блок решения системы алгебраических уравнений, в котором реализуют этот алгоритм, а при решении этой системы дифференциальных уравнений на каждом i-том участке изменения аргумента в этом блоке вычисляют значения дYрi и коэффициентов полиномов дYvi(x), с выхода этого блока подают полученные значения дYрi и этих коэффициентов в блок вычисления приращений интегралов на участке, где с использованием этих значений вычисляют приращения остальных интегралов на этом участке.
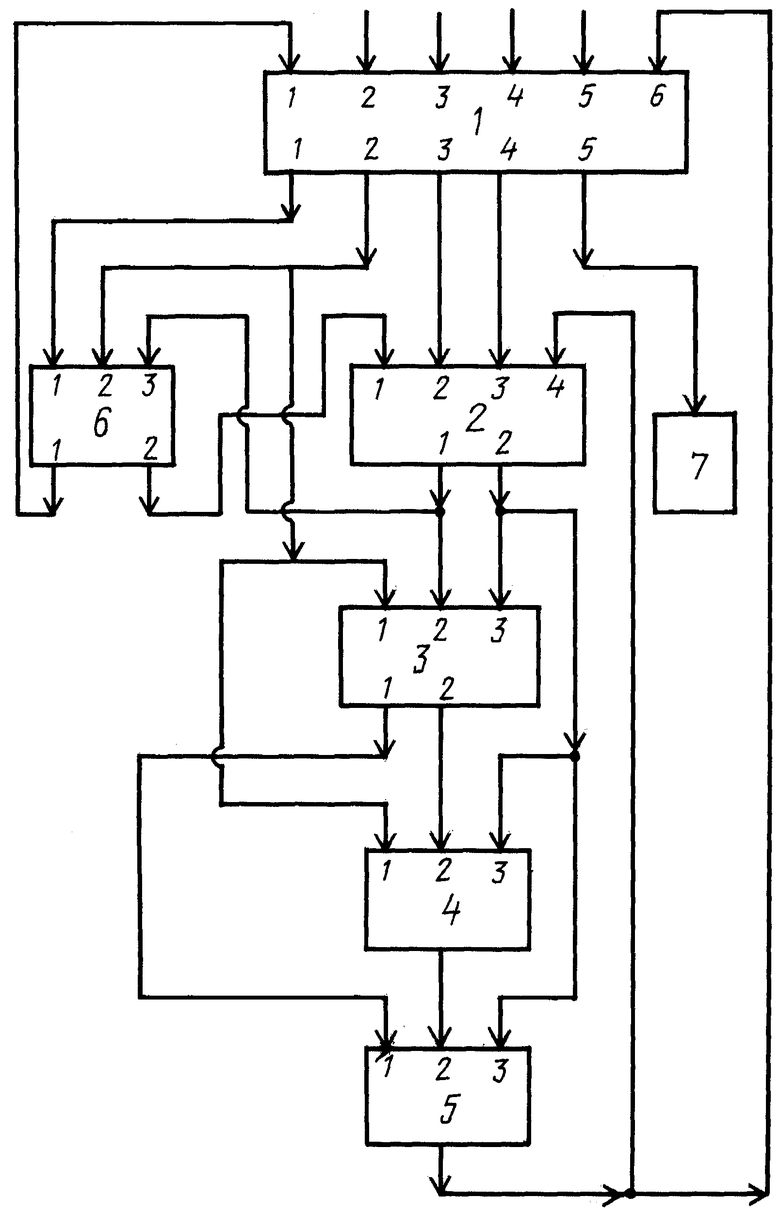
Существо заявляемого изобретения поясняется схемой на фиг.1, где изображена блок-схема возможного варианта устройства, реализующего заявляемый способ. На фиг.1 обозначено: 1 - память вычислителя (ПМ); 2 - блок формирования значений аргумента и интегралов в начале каждого участка (БФ); 3 - блок решения системы алгебраических уравнений (БРСАУ); 4 - блок вычисления приращений интегралов на каждом участке (БВП); 5 - блок вычисления значений интегралов в конце каждого участка (БВИ); 6 - блок вычисления значения аргумента в конце каждого участка и сравнения этого значения с заданным значением Хк (БАС); 7 - устройство вывода (УВ). В блоках и устройствах, которые имеют более одного входа и (или) выхода, соответствующие входы и выходы пронумерованы.
Существо заявляемого изобретения состоит в следующем. Для получения приближенного решения заданной системы дифференциальных уравнений (1) предварительно задают начальное Хо и конечное Хк значения аргумента, ограничивающие интервал его значений, в котором требуется получить это решение, разбивают интервал Хк-Хо изменения аргумента на Q участков, задают длину дХi (i=1, 2, ..., Q) каждого из этих участков так, чтобы сумма длин всех участков была равна заданному интервалу изменения аргумента, и задают начальные значения Yj(Xo) (j=1, 2,..., n) интегралов системы этих уравнений, а в вычислитель устанавливают блок формирования значений аргумента и интегралов в начале каждого участка (БФ), блок вычисления приращений интегралов на каждом участке (БВП), блок вычисления значений интегралов в конце каждого участка (БВИ) и блок вычисления значения аргумента в конце каждого участка и сравнения этого значения с заданным значением Хк (БАС) и вводят значения Хо, Хк, дХi и Yj(Xoi) в память вычислителя.
Также предварительно множество Yj(X) (j=1,2,..., n) интегралов заданной системы дифференциальных уравнений делят на две группы. В первую группу включают интегралы Yp(X) (р=1, 2,..., s), называемые "ключевыми", задание закона изменения каждого из которых на каждом участке в виде соответствующей линейной функции текущего значения
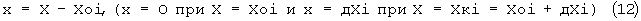
приращения аргумента на этом участке позволяет на этом участке получить аналитическое решение каждого из дифференциальных уравнений этой системы уравнений в виде соответствующей элементарной функции от х. Во вторую группу включают остальные интегралы Yv(X) (v=s+1, s+2,..., n) этой системы дифференциальных уравнений. В результате на каждом участке изменения аргумента заданная система дифференциальных уравнений (1) разделяется на две системы этих уравнений
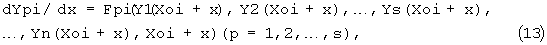
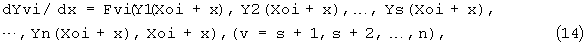
где (13) - система дифференциальных уравнений для "ключевых" интегралов; (14) - система дифференциальных уравнений для остальных интегралов заданной системы дифференциальных уравнений.
Для решения этих систем дифференциальных уравнений задают на этом участке закон изменения каждого из "ключевых" интегралов соответствующей линейной функцией
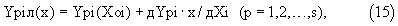
где Ypi(Xoi) - значение соответствующего "ключевого" интеграла в начале рассматриваемого i-того участка; дYрi - неизвестное значение приращения этого интеграла на этом участке.
При подстановке выражений (15) в правые части дифференциальных уравнений (13),(14) получают аналитические решения этих уравнений на этом участке в виде


где дYрiт(х) - закон изменения соответствующего "ключевого" интеграла на рассматриваемом i-том участке; дYvi(х) - закон изменения соответствующего интеграла второй группы на этом участке; Xoi - значение аргумента в начале этого участка; Ypi(Xoi), Yvi(Xoi) -значения соответствующих интегралов в начале этого участка; Фрi(х, дХi, дYрi, Ypi(Xoi), Yvi(Xoi), Xoi), Фvi(х, дYрi, дХi, Ypi(Xoi), Yvi(Xoi), Xoi) - известные элементарные функции указанных аргументов.
Разложением в степенные ряды функции Фрi (16) и Фvi (17) преобразуют в соответствующие полиномы от х

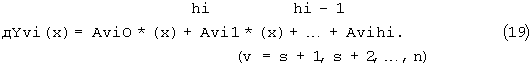
для коэффициентов которых получают соответствующие выражения

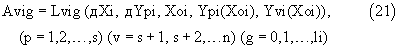
где LpirдXi, дYрi, Xoi, Ypi(Xoi), Yvi(Xoi)), Lvig(дXi, дYрi,Xoi, Ypi(Xoi), Yvi(Xoi)) - известные функции указанных аргументов.
Значения степеней li полиномов (18) и hi полиномов (19) зависят от числа учитываемых членов разложения соответственно функций Фрi (16) и Фvi (17) в степенные ряды, причем с увеличением числа этих членов возрастают значение li и hi и уменьшается ошибка между функциями Фрi (16) и Фvi (17) и соответствующими им степенными рядами. Поэтому для достижения достаточной точности выбирают не менее двух членов в соответствующих степенных рядах, т.е. li>2 и hi>2.
Для вычисления значений дYрi в выражения (18) подставляют выражения (20) и значение

и с учетом того, что по определению

получают систему s алгебраических уравнений относительно дYрi, каждое из которых имеет вид
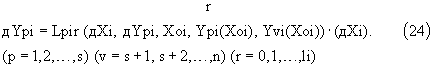
Значения дYрi приращений "ключевых" интегралов вычисляются в результате решения системы алгебраических уравнений (24) известными методами (Бронштейн И.Н., Семендяев К.А., "Справочник по математике для инженеров и учащихся ВТУзов", изд. девятое - М.: Государственное издательство физико-математической литературы, 1962, стр.136-155), в частности, методом получения резольвенты и решения ее методом итераций. При подстановке полученных значений дYрi в выражения (20) и (21) вычисляют значения соответствующих коэффициентов, определяющих полиномы (18) и (19).
Таким образом, в заявляемом методе предварительно составляют систему алгебраических уравнений (24) относительно неизвестных значений дYрi, разрабатывают алгоритм ее решения известными методами и устанавливают в вычислитель дополнительно блок решения системы алгебраических уравнений (БРСАУ), который работает в соответствии с этим алгоритмом.
В начале решения заданной системы дифференциальных уравнений из памяти вычислителя значения Хо и Yj(Xo) подают в БФ, а значения dXi подают в БВП и БАС.
При решении этой системы уравнений на каждом i-том участке в БФ формируют значение Xoi аргумента в начале этого участка

где Хк(i-1) - значение аргумента в конце предыдущего участка; значения интегралов Yj(Xoi) в начале этого участка

где Yj(Xк(i-1)) - значения соответствующих интегралов в конце предыдущего участка. После этого с выхода БФ значение Хоi подают на входы БПВ и БАС, а значения Yj(Xoi) подают на входы БВП и БВИ.
В БРСАУ решают систему алгебраических уравнений (24), в результате чего вычисляют значения дYрi приращений "ключевых" интегралов на этом участке и значения коэффициентов Avig (21). С выхода БРСАУ значения дYрi и Avig (21) подают в БПВ, где вычисляют значения дYvi(дХi) приращений остальных интегралов этой системы на этом участке по формулам
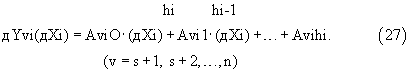
Полученные значения дYрi и дYvi(дХi) приращений всех интегралов на каждом участке с выхода БВП подают в БВИ, где вычисляют значения Ypi(XKi), Yvi(XKi) этих интегралов при значении Хкi аргумента в конце этого участка по формулам


Полученные значения Yр(Хкi), Yv(Xкi) подают в память вычислителя.
В БАС вычисляют значение Хкi аргумента в конце этого участка

и сравнивают значение Хкi с заданным значением Хк. Если

то значения Хкi, Yр(Хкi), Yv(Xкi) подают в БФ и продолжают вычисления на следующем участке. Если же

то прекращают вычисления и значения

подают из памяти вычислителя в устройство вывода, где их демонстрируют на дисплее и (или) печатают на принтере как решение этой системы дифференциальных уравнений.
Для оценки достижения цели изобретения было проведено математическое моделирование процесса падения тела в атмосфере под действием силы тяжести и силы сопротивления воздуха, с учетом изменения плотности атмосферы и скорости звука в воздухе при изменении высоты. Рассматривалась следующая система дифференциальных уравнений, описывающая этот процесс,

где t - время, являющееся аргументом; Y1, Y2, Y3, Y4 - соответственно модуль вектора скорости движения тела, угол ориентации этого вектора в вертикальной плоскости, высота полета тела и расстояние в горизонтальной плоскости между телом и точкой его сброса, являющиеся интегралами системы уравнений (36); Вх, Вн - постоянные коэффициенты; Сх - коэффициент лобового сопротивления тела; g – уcкорение силы тяжести; Vз - скорость звука в воздухе. Система дифференциальных уравнений (33) приближенно интегрировалась при заданной зависимости Сх(Y1/Yз), заданных значениях коэффициентов Вх, Вн и заданных начальных условиях: при t = 0 значения интегралов равны Y1=40 м/с, Y2=0 градусов, Y3=2000 м, Y4=0 м. При использовании заявляемого способа в качестве "ключевого" рассматривался интеграл Y1. Результаты приближенного интегрирования с использованием прототипа и заявляемого способа приведены в таблице 2, где указаны: дХп, дХз - заданная постоянная длина участка изменения аргумента при использовании прототипа (дХп) и заявляемого способа (дХз); Тк - время полета тела до встречи его с землей
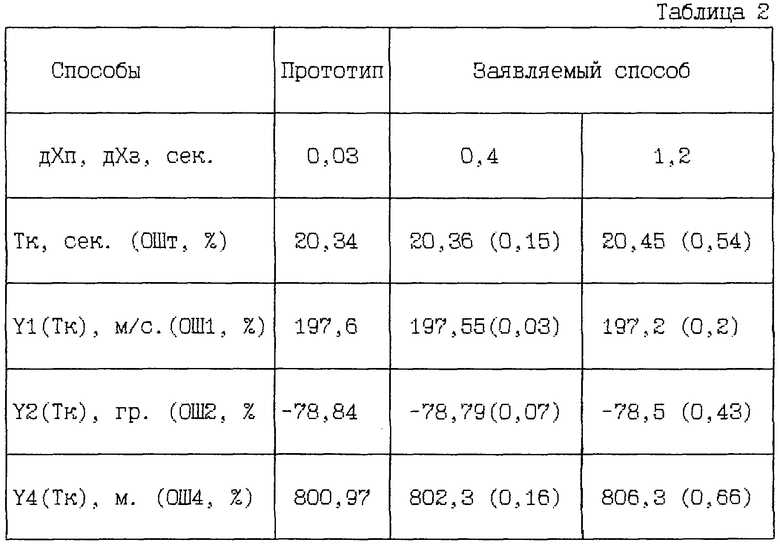
(аналог Хк при Хо = 0); Y1(Тк), Y2(Тк), Y4(Тк) - значения интегралов системы дифференциальных уравнений (33) в момент времени Тк. После значений Тк и интегралов Y1(Тк), Y2(Тк) и Y4(Тк), полученных с использованием заявляемого способа, в скобках приведены значения ОШт, ОШ1, ОШ2, ОШ4 разности между этими значениями и значениями этих параметров, полученными с использованием прототипа, в % относительно значений этих параметров, полученных с использованием прототипа, которые приняты в качестве наиболее точных.
Анализ результатов расчетов, приведенных в таблице 2, позволяет сделать следующие выводы:
- при ошибке результатов, полученных с использованием заявляемого способа, не превышающей 0,2 %, длина дХз участка изменения аргумента при использовании заявляемого способа в 13 раз больше длины дХп участка изменения аргумента при использовании прототипа
дХз=13·дХп;
- при ошибке результатов, полученных с использованием заявляемого способа, не превышающей 0,7 %, длина дХз участка изменения аргумента при использовании заявляемого способа в 40 раз больше длины дХп участка изменения аргумента при использовании прототипа

При сравнении алгоритмов интегрирования системы дифференциальных уравнений (33) с использованием прототипа и заявляемого способа оказалось, что число операций Vуп, которые выполняются на одном участке при использованием прототипа, почти в 4 раза меньше числа операций Vуз, выполняемых на одном участке при использовании заявляемого способа

С учетом выражений (34) и (35), пользуясь формулой (7) при одинаковых значениях Кз и L, получим, что стоимость Сзз материальных затрат на решение этой задачи с ошибкой менее 1 % при использовании заявляемого способа в 10 раз меньше стоимости Сзп материальных затрат на решение этой задачи с использованием прототипа, что и доказывает достижение цели изобретения.
В состав возможного варианта устройства (фиг.1), реализующего предложенный способ, входят ПМ 1, БФ 2, БРСАУ 3, БВП 4, БВИ 5, БАС 6 и УВ 7, причем входы ПМ 1 со второго по пятый электрически связаны с соответствующими выходами системы задания исходных данных, первый вход ПМ 1 электрически связан с первым выходом БАС 6, а шестой вход ПМ 1 электрически связан с выходом БВИ 5, первый выход ПМ 1 электрически связан с первым входом БАС 6, второй выход ПМ 1 электрически связан со вторым входом БАС 6 и первыми входами БРСАУ 3 и БВП 4, третий и четвертый выходы ПМ 1 электрически связаны соответственно со вторым и третьим входами БФ 2, а пятый выход ПМ 1 электрически связан с входом УВ 7, первый вход БФ 2 электрически связан со вторым выходом БАС 6, а четвертый вход БФ 2 электрически связан с выходом БВИ 5, первый выход БФ 2 электрически связан со вторым входом БРСАУ 3 и третьим входом БАС 6, а второй выход БФ 2 электрически связан с третьими входами БВП 4, БРСАУ 3 и БВИ 5, первый выход БРСАУ 3 электрически связан с первым входом БВИ 5, а второй выход БРСАУ 3 электрически связан со вторым входом БВП 4, выход которого электрически связан со вторым входом БВИ 5.
Это устройство работает следующим образом. Предварительно с соответствующих выходов системы задания исходных данных на ПМ 1 подают следующие заданные значения: на второй вход - конечное значение Хк аргумента; на третий вход - начальное значение Хо аргумента; на четвертый вход - значения дХi длины каждого участка, на которые делят заданный диапазон Хк - Хо изменения аргумента; на пятый вход - начальные значения Yj(Xo) (j=1,2,...,n) интегралов заданной системы дифференциальных уравнений.
При решении этой системы уравнений на первом участке дХ1 изменения аргумента с третьего и четвертого выходов ПМ 1 подают соответственно значения Хо и Yj(Xo) на соответствующие входы БФ 2. С первого и второго выходов БФ 2 эти значения на этом участке поступают на соответствующие входы соответствующих блоков этого устройства. На каждом последующем i-том участке изменения аргумента на первый вход БФ 2 подают значение Xк(i-1) аргумента в конце предыдущего участка изменения аргумента, а на четвертый вход БФ 2 подают значения Yj(Xк(i-1)) интегралов в конце предыдущего участка изменения аргумента и в соответствии с алгоритмом (25), (26) формируют в БФ 2 значения Xoi аргумента и Yj(Xoi) интегралов в начале этого участка, которые соответственно с первого и второго выходов БФ 2 подают на соответствующие входы соответствующих блоков устройства.
Так, значения Xoi и Yj(Xoi) подают соответственно на второй и третий входы БРСАУ 3, а на его первый вход со второго выхода ПМ 1 подают значение дХi длины этого участка. В БРСАУ 3 с использованием этих значений решают систему алгебраических уравнений (24), в результате чего вычисляют значения дYрi приращений "ключевых" интегралов на этом участке изменения аргумента и значения коэффициентов Avi0, Avi1,..., Avihi полиномов дYvi(дХi) (27).
Со второго выхода БРСАУ 3 значения Avi0, Avi1,..., Avihi подают на второй вход БПВ 4. На первый вход БПВ 4 со второго выхода ПМ 1 подают значение дХi, а на третий вход БПВ 4 со второго выхода БФ 2 подают значения Yj(Xoi). В БПВ 4 с использованием этих значений вычисляют приращения дYvi(дХi) (27) остальных интегралов на этом участке, которые с выхода БПВ 4 подают на второй вход БВИ 5. На первый и третий входы БВИ 5 подают соответственно значения дYрi и Yj(Xoi) с соответствующих выходов БРСАУ 3 и БФ 2. В БВИ 5 вычисляют значения Ypi(Xкi) (28) и Yvl(Xкi) (29) интегралов, являющихся значениями Yj(Xкi) интегралов в конце этого участка изменения аргумента, которые с выхода БВИ 5 подают на шестой вход ПМ 1.
В БАС 6 с использованием значений Xoi и дХi, которые подают на второй и третий входы БАС 6 с соответствующих выходов БФ 2 и ПМ 1, вычисляют значение Хкi (30) аргумента в конце этого участка. В БАС 6 также сравнивают значения Хкi и Хк. Если выполняется соотношение (31), то со второго выхода БАС 6 значение Хкi подают на первый вход БФ 2, а с выхода БВИ 5 значения Yj(XKi) подают на четвертый вход БФ 2 и продолжают вычисления на следующем участке изменения аргумента. Если же выполняется соотношение(32), то с первого выхода БАС 6 на первый вход ПМ 1 подают соответствующий сигнал, по которому все значения Yj(Xкi) с пятого выхода ПМ 1 подают на вход УВ 7, где их демонстрируют на дисплее и (или) печатают на принтере как решение заданной системы дифференциальных уравнений.
Источники информации
1. Зельдович Я.Б., Мышкис А.Д., Элементы прикладной математики, - М.: Наука, 1972 г., стр.261-263.
2. Березин И.С., Жидков Н.П., "Методы вычислений", том 2 - М., Государственное издательство физико -математической литературы, 1962 г., стр.292-333.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ЗНАЧЕНИЙ ПАРАМЕТРОВ ТРАЕКТОРИИ БОМБЫ | 2002 |
|
RU2212620C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГРАНИЦ ОБЛАСТИ ВОЗМОЖНОГО ПУСКА РАКЕТЫ | 2001 |
|
RU2206044C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ СКОРОСТИ ВЕТРА | 2001 |
|
RU2206112C1 |
| Интегро-арифметическое устройство | 1979 |
|
SU783813A1 |
| Цифровое устройство для воспроизведения кусочно-линейных функций | 1978 |
|
SU771671A1 |
| СПОСОБ НАВЕДЕНИЯ УПРАВЛЯЕМОГО ОБЪЕКТА НА ЦЕЛЬ | 1997 |
|
RU2117312C1 |
| СПОСОБ НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА ЦЕЛЬ | 2001 |
|
RU2204785C2 |
| Устройство для вычисления полиномов | 1978 |
|
SU792263A1 |
| СПОСОБ ДИСТАНЦИОННОГО ОПРЕДЕЛЕНИЯ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ НАЗЕМНОГО ОБЪЕКТА | 2000 |
|
RU2182713C2 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ПЕРЕДАЧИ И ПРИЕМА СИГНАЛОВ С ОГРАНИЧЕННЫМ СПЕКТРОМ (ВАРИАНТЫ) | 2004 |
|
RU2265278C1 |
Изобретение относится к способам численного решения системы дифференциальных уравнений (СДУ). Техническим результатом является снижение стоимости материальных затрат, необходимых для точного решения СДУ. Это достигается за счет того, что предварительно задают начальное Хо, конечное Хк значения аргументов и начальные значения интегралов Yj (Xo), интервал Хк - Хо разбивают на Q участков длиной dXi (i=1...Q), а интегралы делят на две группы: “ключевые” интегралы Yp (р=1,..., S), задание изменения каждого из которых позволяет аналитически решить каждое дифференциальное уравнение этой системы и остальные интегралы Yv(x)(v=s+1,..., n). 1 ил., 2 табл.
Способ численного решения системы дифференциальных уравнений, который состоит в том, что предварительно задают начальное Хо и конечное Хк значения аргумента, ограничивающие интервал значений, в котором будут решать эту систему уравнений, разбивают этот интервал на Q участков и задают длину дХi (i=1, 2,... Q) каждого участка так, чтобы сумма дХi была равна этому интервалу, задают начальные значения Yj (Xo) (j=1, 2,..., n) интегралов этой системы уравнений, в вычислитель устанавливают блок формирования значений аргумента и интегралов в начале участка, блок вычисления приращений интегралов на участке, блок вычисления значений интегралов в конце участка и блок вычисления значения аргумента в конце участка и сравнения с Хк, а в память вычислителя вводят значения Хо, Хк, дХi и Yj (Хо), в начале решения этой системы уравнений из памяти вычислителя значения Хо и Yj (Хо) подают в блок формирования значений аргумента и интегралов в начале участка, а значения дXi подают в блок вычисления приращений интегралов на участке и в блок вычисления значения аргумента в конце участка и сравнения с Хк, в который из памяти вычислителя также подают значение Хк, при решении этой системы уравнений на каждом i-том участке в блок формирования значений аргумента и интегралов в начале участка подают значение Хк(i-1) аргумента и значения Yj (Xк(i-1)) интегралов в конце предыдущего участка и формируют в этом блоке значение Xoi аргумента в начале этого участка, равное значению Хк(i-1), и значения Yj(Xoi) интегралов в начале этого участка, равные значениям Yi (Xк (i-1)), и значение Xoi подают в блок вычисления приращений интегралов на участке и в блок вычисления значения аргумента в конце участка и сравнения с Хк, а значения Yj (Хоi) подают в блок вычисления приращений интегралов на участке и в блок вычисления значений интегралов в конце участка, в блоке вычисления приращений интегралов на участке вычисляют приращение каждого интеграла на этом участке и с выхода этого блока подают эти приращения в блок вычисления значений интегралов в конце участка, где суммируют значение Yi (Xoi) каждого интеграла с его приращением и получают значения Yj (Xкi) интегралов в конце этого участка, которые подают в память вычислителя, а в блоке вычисления значения аргумента в конце участка и сравнения с Хк суммируют значения Xoi и дХi и получают значение Хкi аргумента в конце этого участка, которое сравнивают с Хк, причем, если Хкi меньше Хк, то подают значения Хкi и Yj (Xкi) в блок формирования значений аргумента и интегралов в начале участка и продолжают решение этой системы уравнений на следующем участке, а если Хкi=Хк, то формируют сигнал, по которому прекращают решение этой системы уравнений и из памяти вычислителя подают значения Yi (Xкi) (j=1, 2,..., n; i=1, 2..., Q) на устройство вывода и демонстрируют эти значения на дисплее и (или) печатают их на принтере, отличающийся тем, что предварительно множество Yj (j=1, 2,..., n) интегралов этой системы уравнений делят на две группы, первая из которых содержит интегралы Yp (p=1, 2,..., s; s<n), называемые “ключевыми”, задание закона изменения каждого из которых на каждом участке изменения аргумента в виде соответствующей линейной функции позволяет получить аналитическое решение каждого дифференциального уравнения этой системы на этом участке, а вторая группа содержит остальные интегралы Yv (v=s+1, s+2,..., n) этой системы уравнений, на каждом участке изменения аргумента закон изменения каждого из “ключевых” интегралов задают соответствующей линейной функцией Ypiл (х) текущего значения х приращения аргумента на этом участке, зависящей от неизвестного значения дYpi приращения этого интеграла на этом участке, значения Ypi (Xoi) этого интеграла в начале этого участка и дХi, с использованием функций Ypiл (х) получают аналитические решения дифференциальных уравнений этой системы, в результате преобразования которых получают полиномы дYvi (х), дYpi (х) не ниже второй степени, определяющие изменение приращений соответствующих интегралов на этом участке, и систему алгебраических уравнений относительно значений дYpi, разрабатывают алгоритм решения этой системы алгебраических уравнений и дополнительно устанавливают в вычислитель блок решения этой системы алгебраических уравнений, на входы которого на каждом i-том участке подают значения Xoi, Yj (Xoi) и дХi и в этом блоке по разработанному алгоритму вычисляют значения дYpi и коэффициентов полиномов дYvi (x), с выхода этого блока подают полученные значения дYpi и этих коэффициентов в блок вычисления приращений интегралов на этом участке, где с использованием этих значений вычисляют приращения остальных интегралов на этом участке.
| БЕРЕЗИН И.С | |||
| и др | |||
| Методы вычислений | |||
| - М.: Госуд | |||
| изд-во физико-математической литературы, 1962, т.2, с.292-333 | |||
| УСТРОЙСТВО N-КРАТНОГО ДИФФЕРЕНЦИРОВАНИЯ | 1999 |
|
RU2160922C1 |
| УСТРОЙСТВО ДИФФЕРЕНЦИРОВАНИЯ | 1998 |
|
RU2148271C1 |
| US 4293918 А, 06.10.1981 | |||
| СПОСОБ ОПРЕДЕЛЕНИЯ КАЧЕСТВА ГОМЕОПАТИЧЕСКИХ ЛЕКАРСТВЕННЫХ СРЕДСТВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 1997 |
|
RU2112976C1 |
Авторы
Даты
2004-12-20—Публикация
2003-03-13—Подача