Текст описания приведен в факсимильном виде. 
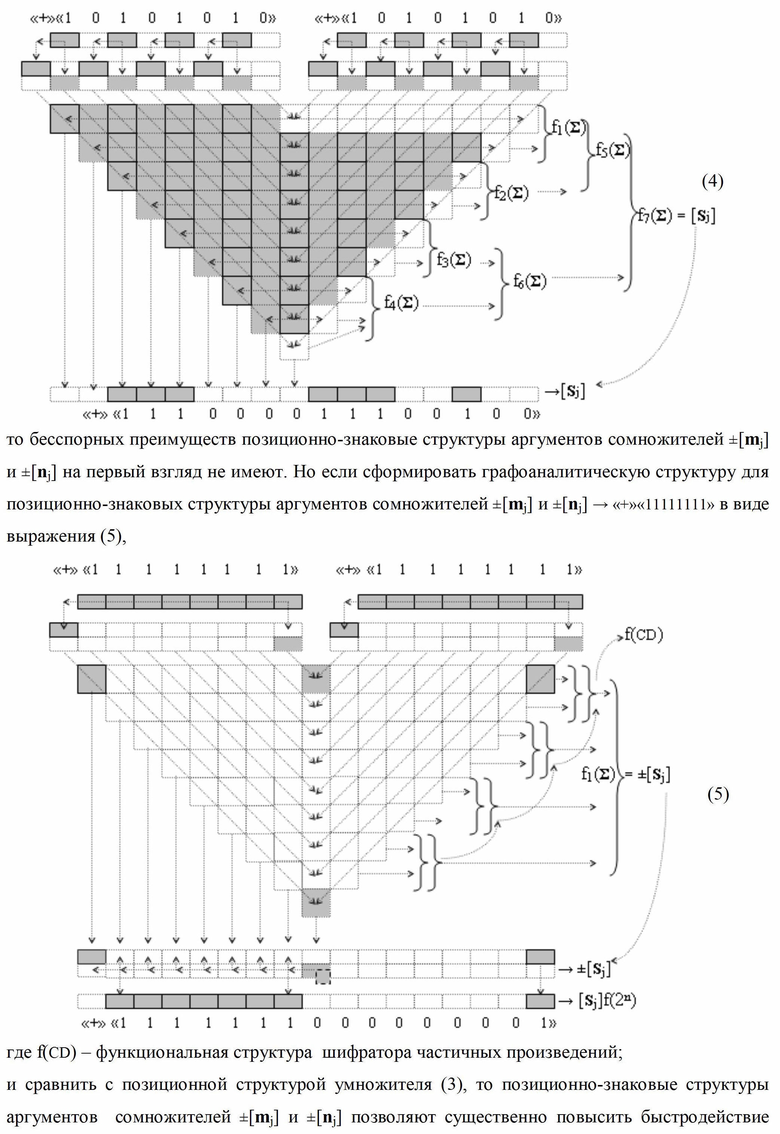
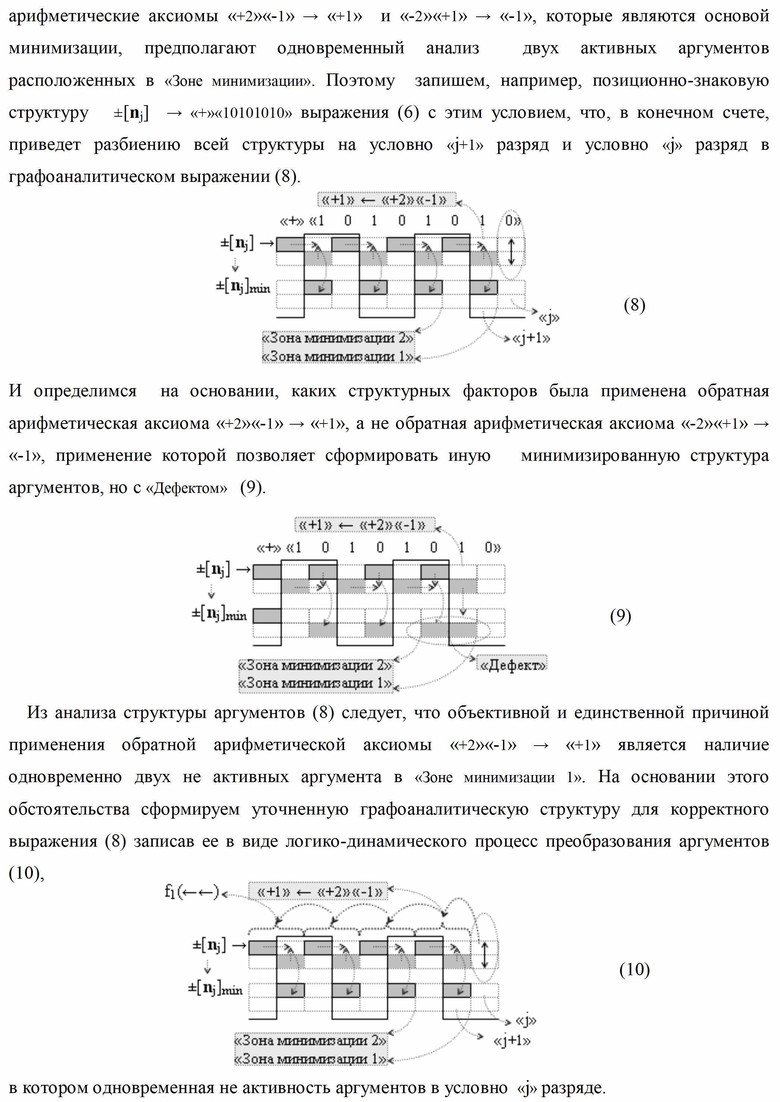
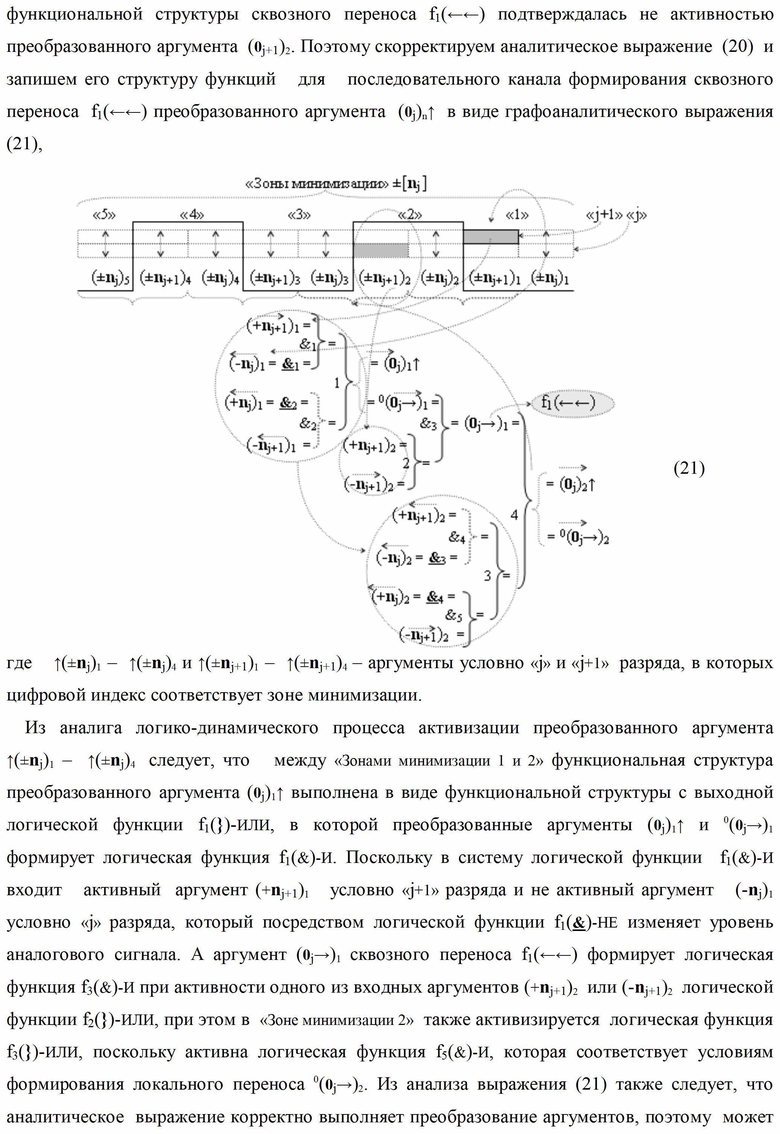
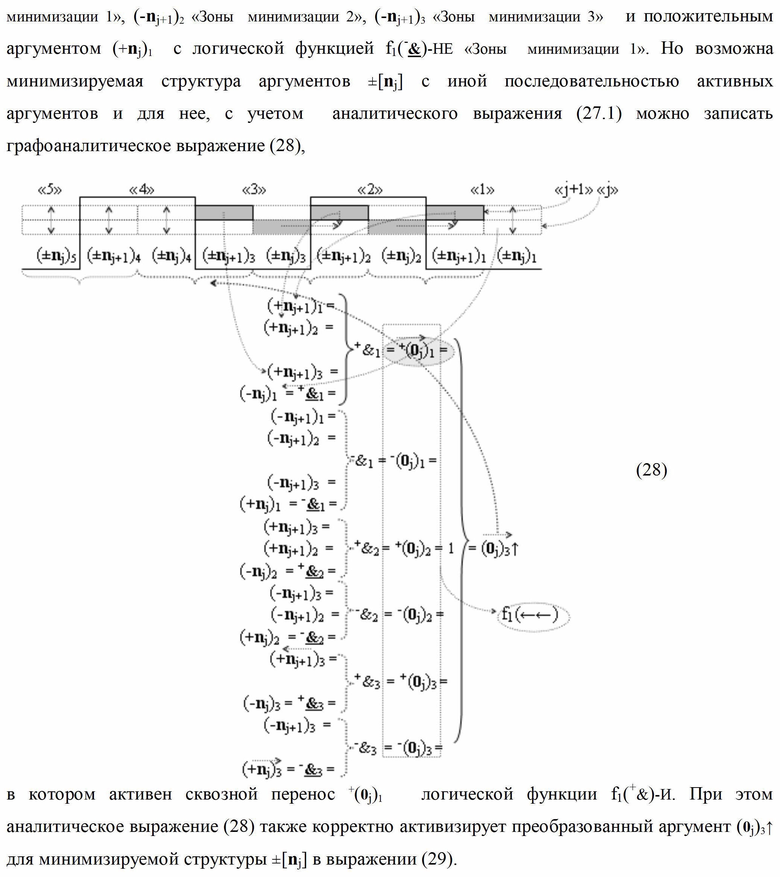
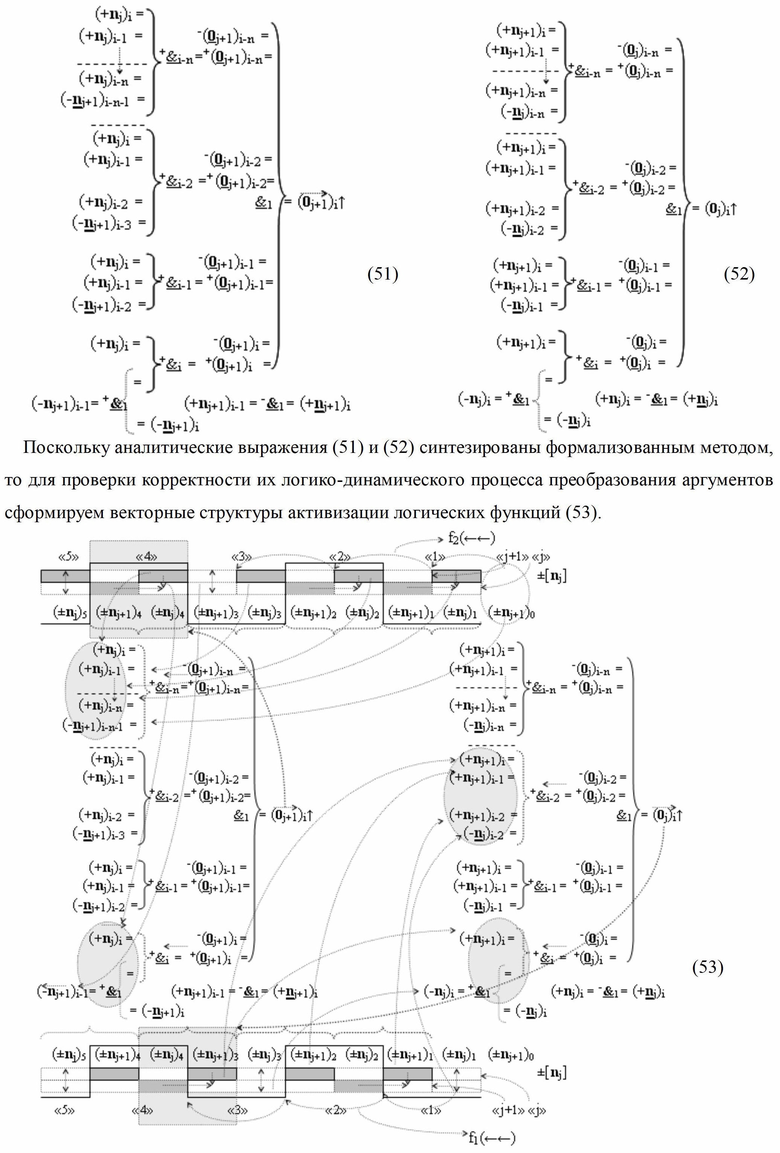
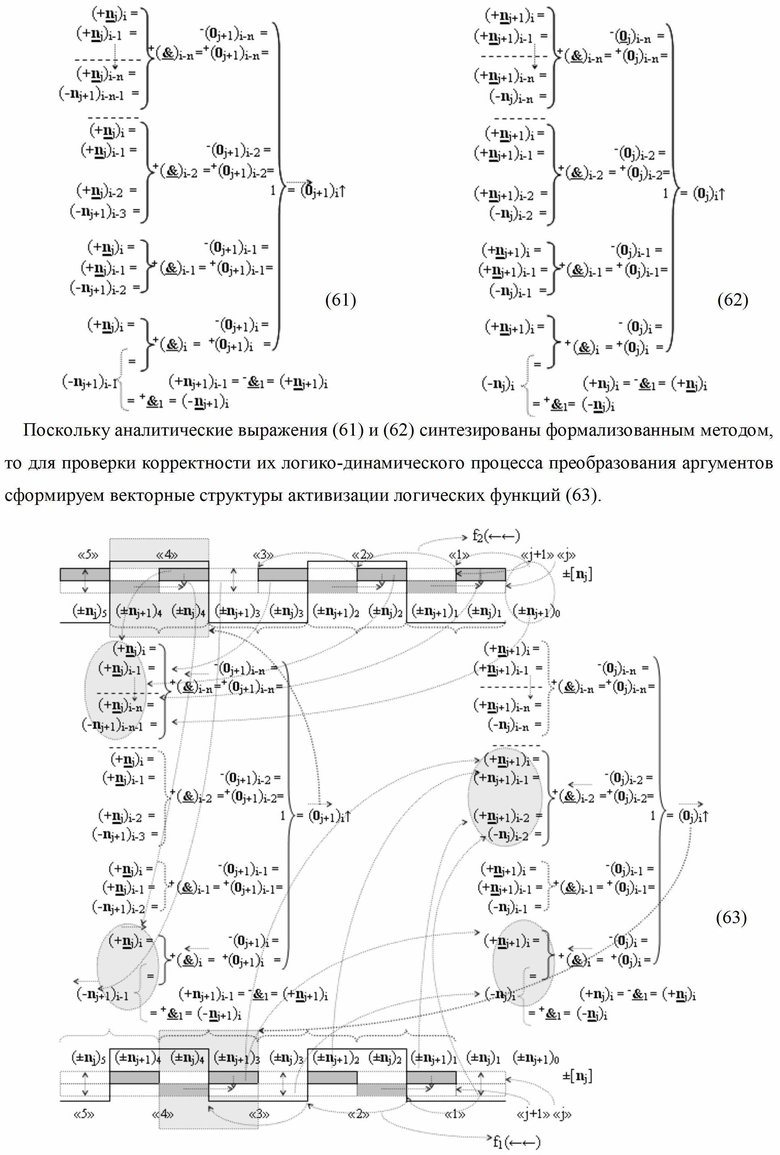
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнении арифметических операций суммирования и вычитания в позиционно-знаковых кодах. Техническим результатом является повышение быстродействия процесса преобразования аргументов при формировании сквозного параллельного переноса f(←←). В одном варианте функциональная структура выполнена с использованием элементов, реализующих логические функции И, ИЛИ и НЕ. При этом функциональная структура условно «i»-ой зоны минимизации выполнена в виде двух эквивалентных структур логических функций - функциональной логической структуры параллельного переноса f1(←←) для формирования преобразованного аргумента (0j)i и функциональной логической структуры f2(←←) для формирования преобразованного аргумента (0j+1→)i. 5 н.п. ф-лы.
1. Способ формирования преобразованных аргументов аналоговых сигналов (0
j)i и (0
j+1)i сквозного параллельного переноса f(←←) для преобразования позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) в условной «i» зоне минимизации, который включает одновременный анализ на логическом уровне активность как аргументов аналогового сигнала в условно «i» зоне минимизации, так и одновременную активность одного из аргументов аналогового сигнала в непрерывной его последовательности в предыдущих зонах минимизации, отличающийся тем, что одновременный анализ позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) для последующей их минимизации выполняют посредством двух функциональных логических структур параллельного переноса f1(←←) и f2(←←), которые активизируют либо преобразованный аргумент аналогового сигнала (0
j)i для минимизации аргументов ±[n
j]f(+/-) между «i+1» и «i» зонами минимизации, либо активизируют преобразованный аргумент аналогового сигнала (0
j+1)i для минимизации аргументов ±[n
j]f(+/-) в «i+1» зоне минимизации, при этом преобразованный аргумент аналогового сигнала (0
j)i в первой функциональной логической структуре активизируют как при активном позиционно-знаковом положительном аргументе (+n
j+1)i или условно отрицательном аргументе (-n
j+1)i условно «j+1» разряда и неактивном условно отрицательном аргументе (-n
j)i или положительном аргументе (+n
j)i условно «j» разряда, так и при всех неактивных аргументах (-n
j)i-1 - (-n
j)i-n, где n - число, не превышающее «i+1» зоны минимизации, для которых в промежуточных зонах минимизации положительные или условно отрицательные одноименные по знаку аргументы активны в соответствии с логико-динамическим процессом преобразования аргументов аналоговых сигналов вида
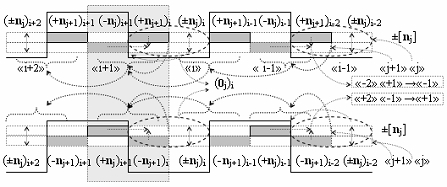
а преобразованный аргумент аналогового сигнала (0
j+1)i во второй функциональной логической структуре активизируют как при активном позиционно-знаковом положительном аргументе (+n
j)i или условно отрицательном аргументе (-n
j)i «j» разряда и неактивном условно отрицательном аргументе (-n
j+1)i-1 или положительном аргументе (+n
j+1)i-1 «i-1» зоны минимизации, так и при всех неактивных аргументах (-n
j+1)i-2 - (-n
j+1)i-n-1, для которых в промежуточных зонах минимизации положительные или условно отрицательные одноименные по знаку аргументы активны в соответствии с логико-динамическим процессом преобразования аргументов аналоговых сигналов вида
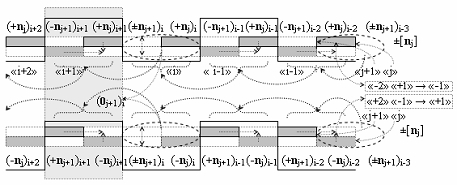
2. Функциональная структура формирования преобразованных аргументов аналоговых сигналов (0
j)i и (0
j+1)i сквозного параллельного переноса f(←←) для преобразования позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) в условной «i» зоне минимизации, в которой условно «i» зона минимизации включает логические функции f1(+
&
)-НЕ и f1(-
&
)-НЕ, в которой функциональная выходная связь является функциональной входной связью логической функции fi(+&)-И и fi(-&)-И, а также включает две логические функции f1(})-ИЛИ, при этом функциональная структура условно «i» зоны минимизации выполнена в виде функциональной логической структуры параллельного переноса f1(←←) для формирования преобразованного аргумента (0
j)i и функциональной логической структуры параллельного переноса f2(←←) для формирования преобразованного
аргумента(0
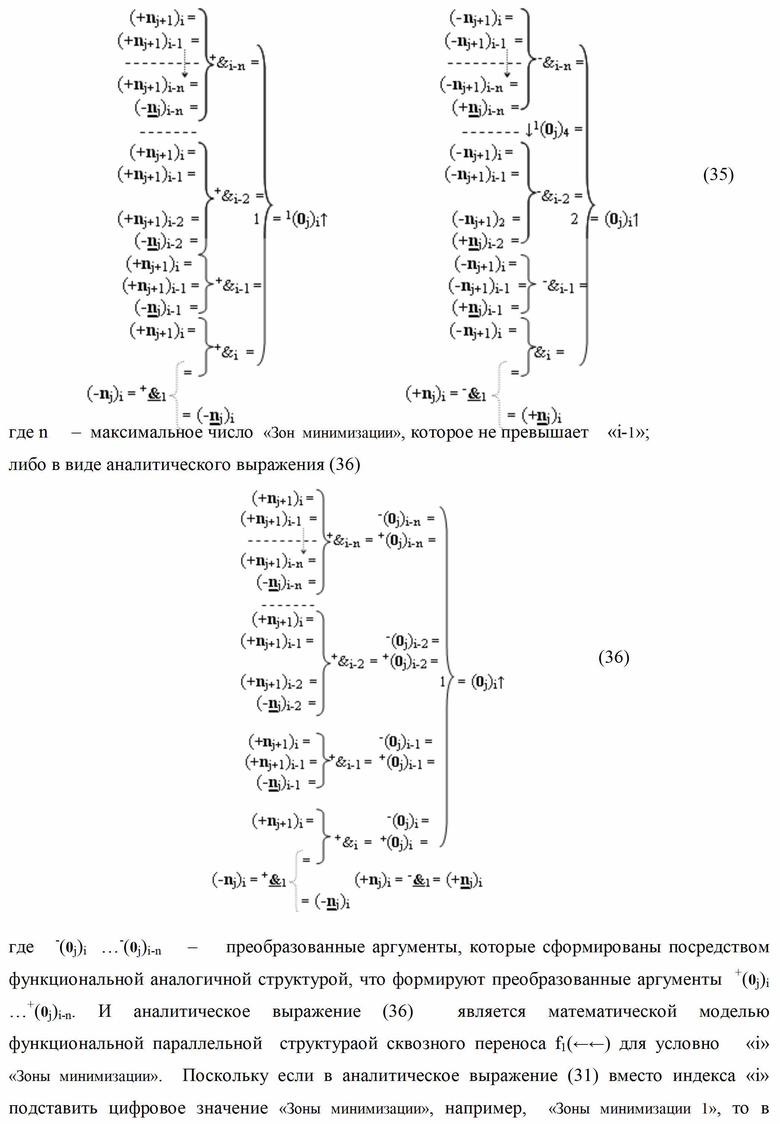
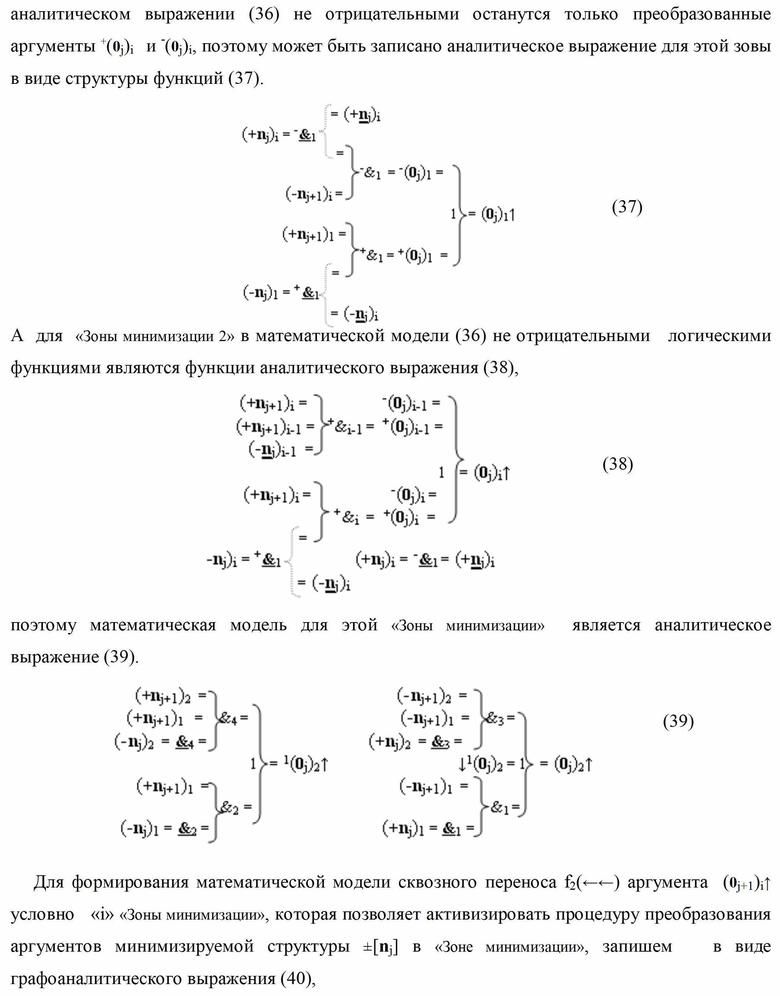
j+1)i, которые имеют эквивалентную структуру логических функций, отличающаяся тем, что в каждую из них дополнительно введены логические функции fi-1(+&)-И - fi-n(+&)-И и fi-1(-&)-И - fi-n(-&)-И, при этом функциональные связи логических функций в структуре формирования сквозного параллельного переноса f(←←) выполнены в соответствии с математической моделью вида
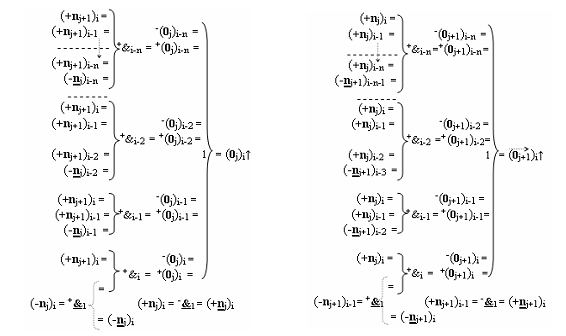
где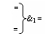 
- логическая функция f1(&)-И; 
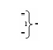- логическая функция f1(})-ИЛИ.
3. Функциональная структура формирования преобразованных аргументов аналоговых сигналов (0
j)i и (0
j+1)i сквозного параллельного переноса f(←←) для преобразования позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) в условной «i» зоне минимизации, в которой условно «i» зона минимизации включает логические функции f1(+
&
)-НЕ и f1(-
&
)-НЕ, при этом функциональная структура условно «i» зоны минимизации выполнена в виде функциональной логической структуры параллельного переноса f1(←←) для формирования преобразованного аргумента (0
j)i и функциональной логической структуры параллельного переноса f2(←←) для формирования преобразованного аргумента(0
j+1)i, которые имеют эквивалентную структуру логических функций, отличающаяся тем, что в каждую из них дополнительно введены логические функции fi(+&)-И-НЕ - fi-n(+&)-И-НЕ и fi(-&)-И-НЕ - fi-n(-&)-И-НЕ, при этом функциональные связи логических функций в структуре формирования сквозного параллельного переноса f(←←) выполнены в соответствии с математической моделью вида
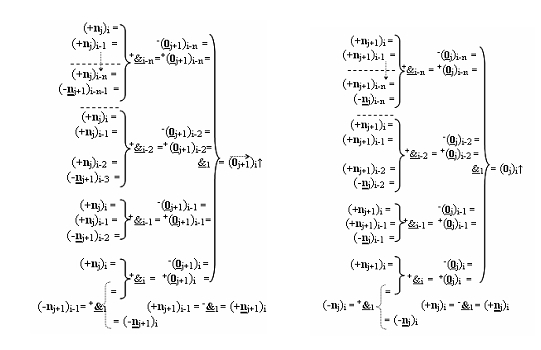
где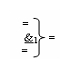 
- логическая функция f1(&)-И-НЕ.
4. Функциональная структура формирования преобразованных аргументов аналоговых сигналов (0
j)i и (0
j+1)i сквозного параллельного переноса f(←←) для преобразования позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) в условной «i» зоне минимизации, в которой условно «i» зона минимизации включает логические функции f1(+
&
)-НЕ и f1(-
&
)-НЕ, а также включает две группы логических функций fi(+
})-ИЛИ - fi-n(+
})-ИЛИ и fi(-
})-ИЛИ - fi-n(-
})-ИЛИ, при этом функциональная структура условно «i» зоны минимизации выполнена в виде функциональной логической структуры параллельного переноса f1(←←) для формирования преобразованного аргумента (0
j)i и функциональной логической структуры параллельного переноса f2(←←) для формирования преобразованного аргумента(0
j+1)i, которые имеют эквивалентную структуру логических функций, отличающаяся тем, что в каждую из них дополнительно введены логические функции f1(+&)-И-НЕ и f1(-&)-И-НЕ, при этом функциональные связи логических функций в структуре формирования сквозного параллельного переноса f(←←) выполнены в соответствии с математической моделью вида
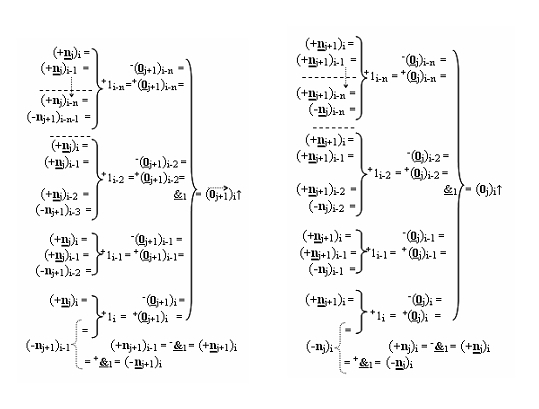
5. Функциональная структура формирования преобразованных аргументов аналоговых сигналов (0
j)i и (0
j+1)i сквозного параллельного переноса f(←←) для преобразования позиционно-знаковых аргументов аналоговых сигналов ±[n
j]f(+/-) в условной «i» зоне минимизации, в которой условно «i» зона минимизации включает логические функции f1(+
&
)-НЕ и f1(-
&
)-НЕ и две логические функции f1(})-ИЛИ, отличающаяся тем, что функциональная структура условно «i» зоны минимизации выполнена в виде функциональной логической структуры параллельного переноса f1(←←) для формирования преобразованного аргумента (0
j)i и функциональной логической структуры параллельного переноса f2(←←) для формирования преобразованного аргумента(0
j+1)i, которые имеют эквивалентную структуру логических функций, при этом в каждую из них дополнительно введены логические функции fi(+
}&
)-ИЛИ-НЕ - fi-n(+
}&
)-ИЛИ-НЕ и fi(-
}&
)-ИЛИ-НЕ - fi-n(-
}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре формирования сквозного параллельного переноса f(←←) выполнены в соответствии с математической моделью вида
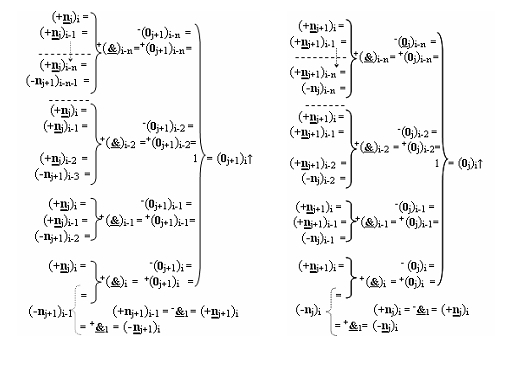
где 
- логическая функция f1(}&
)-ИЛИ-НЕ.
| УЭЙКЕРЛИ Д | |||
| Проектирование цифровых устройств | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| - М.: «Постмаркет», 2002, с.502, рис.5.86 | |||
| Блок формирования сквозного переноса в сумматоре | 1984 |
|
SU1196852A1 |
| Устройство для формирования сигнала переноса при суммировании многофазных кодов | 1989 |
|
SU1633393A1 |
| RU 2007146288 A, 27.06.2009 | |||
| JP 2002312160 A, 25.10.2002 | |||
| US 5600583 A, 04.02.1997. | |||
