Текст описания приведен в факсимильном виде.





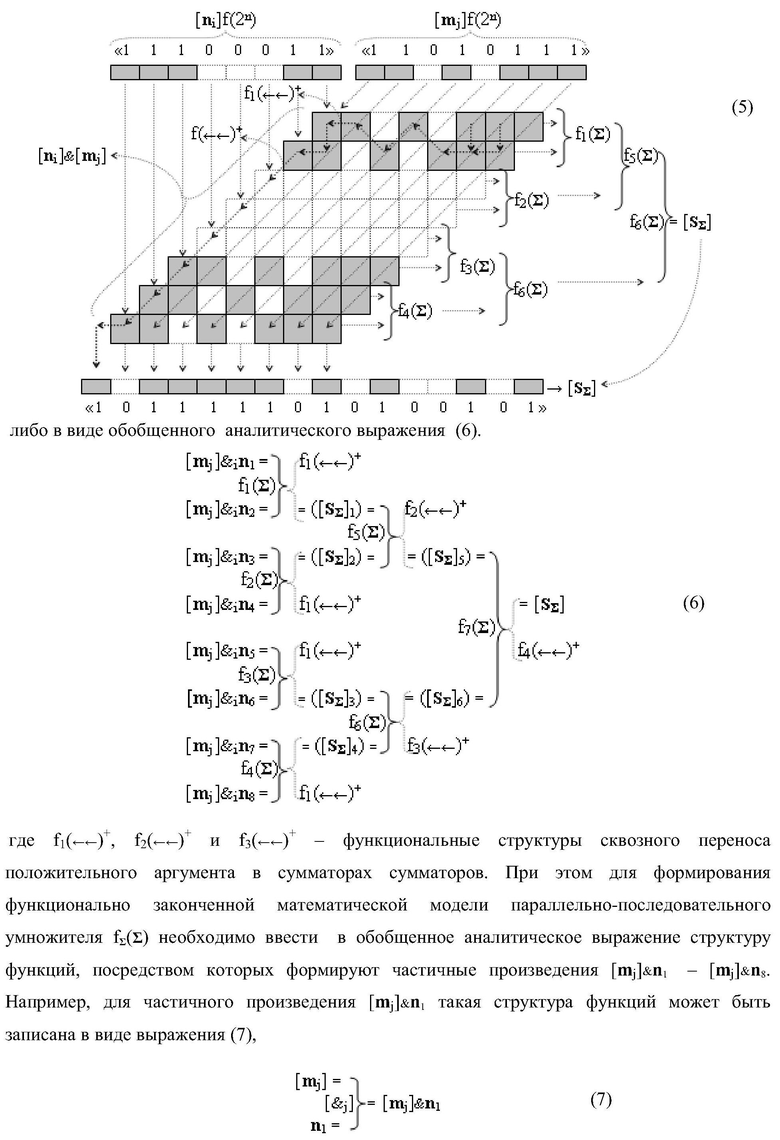



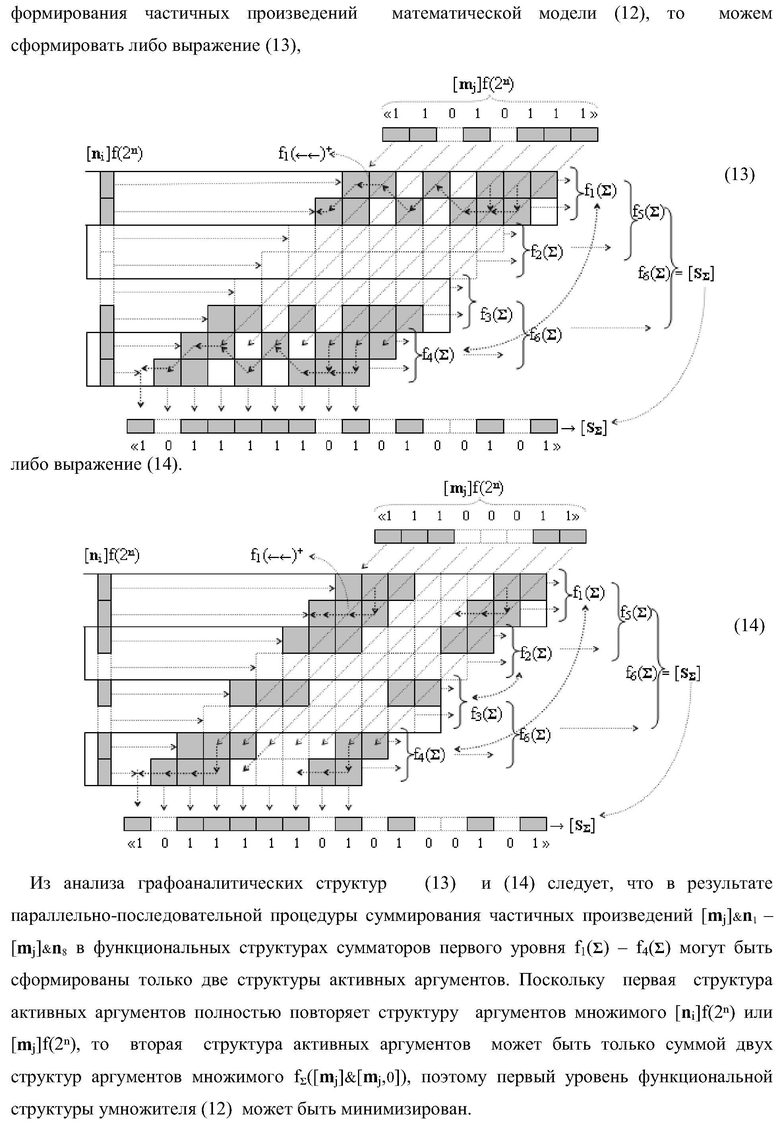






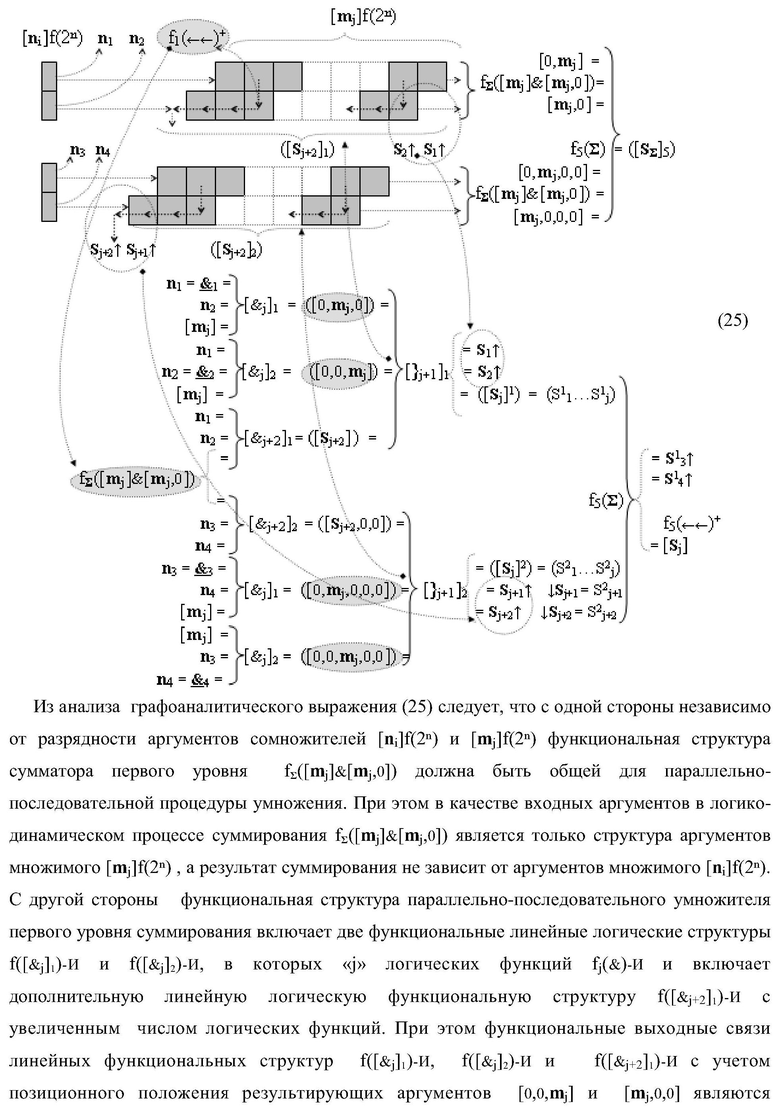


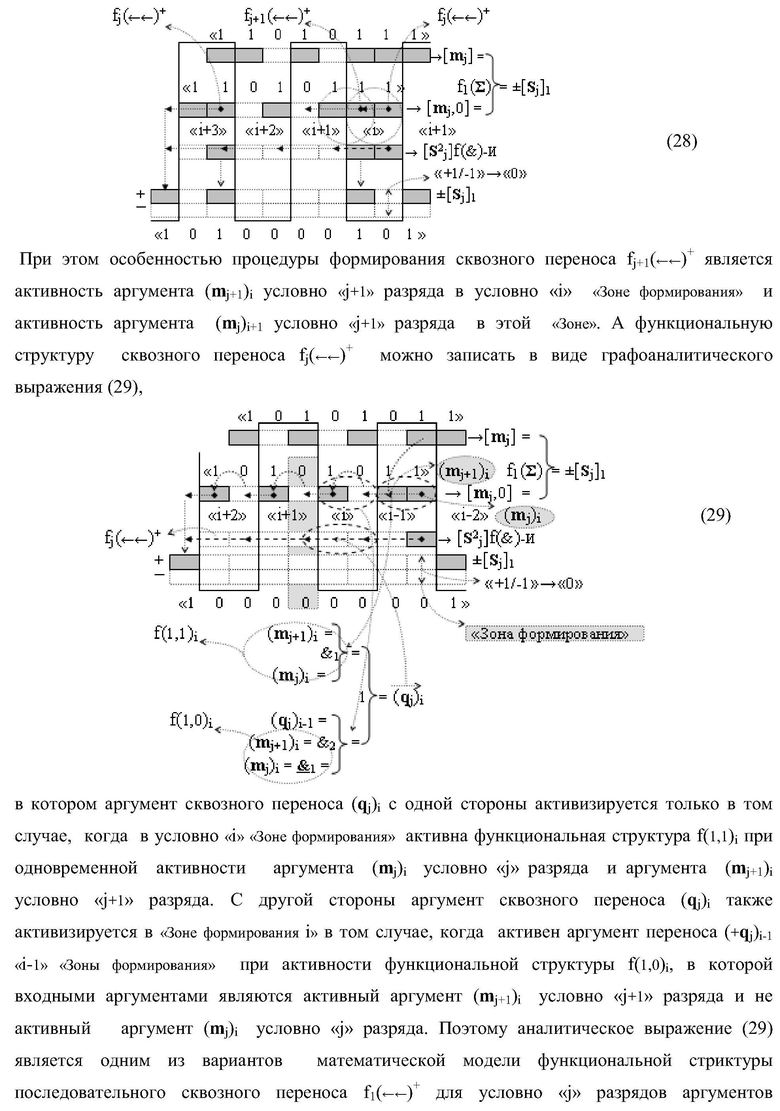





Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических операций суммирования в параллельно-последовательном умножителе. Техническим результатом является повышение быстродействия процедуры формирования сквозного последовательного переноса в предварительном сумматоре умножителя. В одном из вариантов изобретения в «i»-й «зоне формирования», включающей «j+1»-й и «j»-й разряды, функциональные структуры выполнены эквивалентными, при этом каждая функциональная структура содержит элементы, реализующие логические функции И, ИЛИ. 4 н.п. ф-лы.
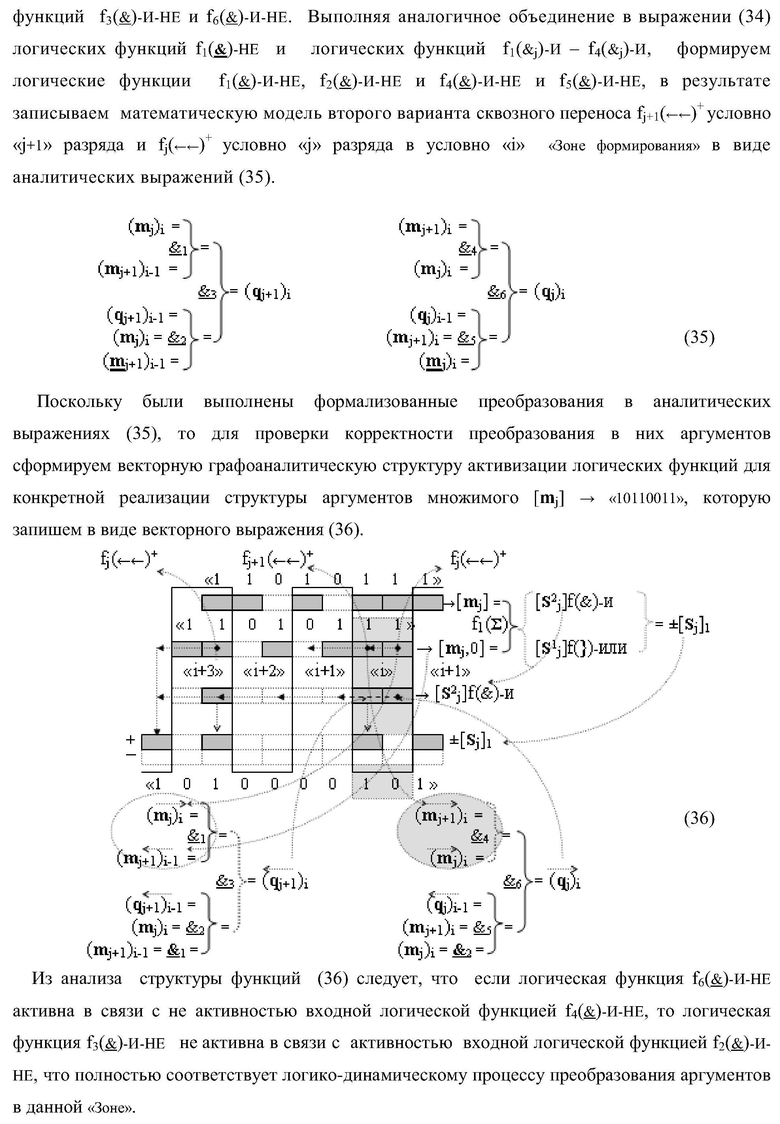
1. Функциональная структура последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для корректировки результирующей суммы предварительного суммирования активных аргументов множимого [m
j]f(2n) позиционного формата параллельно-последовательного умножителя fΣ(Σ), включающая логические функции f1(})-ИЛИ и f2(})-ИЛИ, в которых функциональные выходные связи являются функциональными выходными связями структуры условной «i» зоны минимизации для формирования аргумента переноса (q
j+1)i и (q
j)i, а две их функциональные входные связи являются функциональными выходными связями соответственно логических функций f1(&)-И, f2(&)-И и f3(&)-И, f4(&)-И, в которых одна функциональная входная связь является функциональной входной связью структуры последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для приема аргументов множимого (m
j)i и (m
j+1)i, отличающаяся тем, что функциональные структуры последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для «j+1» разряда и «j» разряда выполнены в виде функционально независимых структур, а функциональные связи логических функций выполнены в соответствии с математической моделью вида
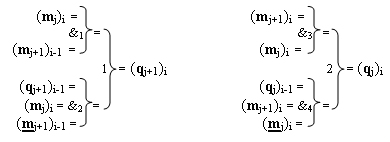
где 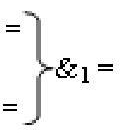 - логическая функция f1(&)-И;
- логическая функция f1(&)-И; 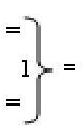 - логическая функция f1(})-ИЛИ;
- логическая функция f1(})-ИЛИ;
«=&
1=» - логическая функция f1(
&
)-НЕ изменения активности входных аналоговых сигналов.
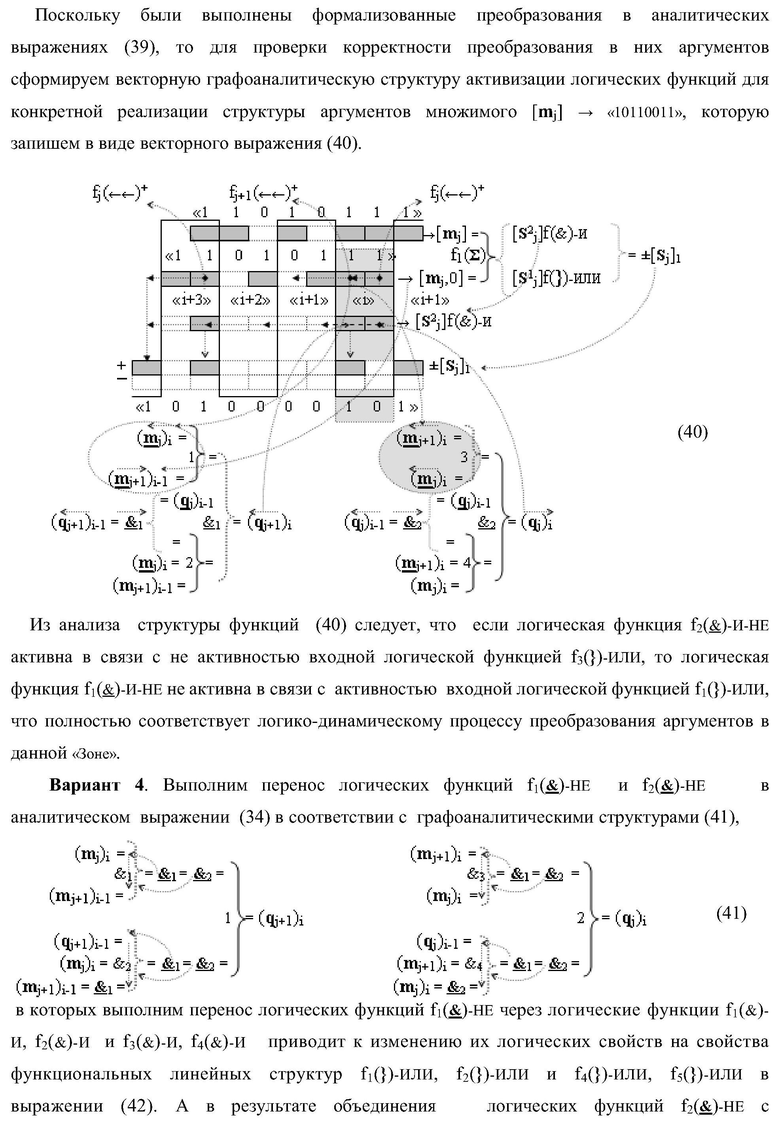
2. Функциональная структура последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для корректировки результирующей суммы предварительного суммирования активных аргументов множимого [m
j]f(2n) позиционного формата параллельно-последовательного умножителя fΣ(Σ), отличающаяся тем, что функциональные структуры последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для «j+1» разряда и «j» разряда выполнены в виде функционально независимых структур, в которые введены логические функции f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ и f4(&)-И-НЕ, f5(&)-И-НЕ, f6(&)-И-НЕ соответственно, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида
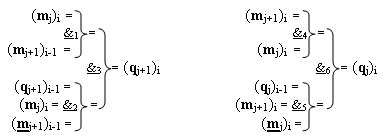
где 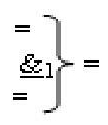 - логическая функция f1(&)-И-НЕ;
- логическая функция f1(&)-И-НЕ;
3. Функциональная структура последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для корректировки результирующей суммы предварительного суммирования активных аргументов множимого [m
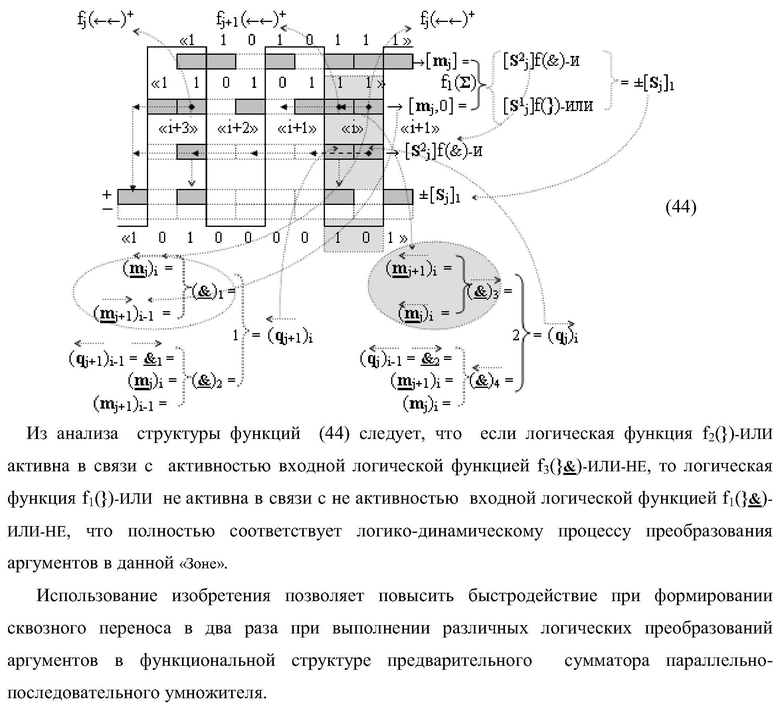
j]f(2n) позиционного формата параллельно-последовательного умножителя fΣ(Σ), включающая логические функции f1(})-ИЛИ и f3(})-ИЛИ, отличающаяся тем, что функциональные структуры последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для «j+1» разряда и «j» разряда выполнены в виде функционально независимых структур, в которые введены логические функции f1(
&
)-НЕ, f2(})-ИЛИ, f1(&)-И-НЕ и f2(
&
)-НЕ, f4(})-ИЛИ, f2(&)-И-НЕ соответственно, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида
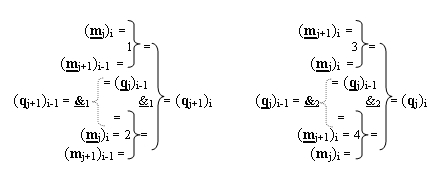
4. Функциональная структура последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для корректировки результирующей суммы предварительного суммирования активных аргументов множимого [m
j]f(2n) позиционного формата параллельно-последовательного умножителя fΣ(Σ), включающая логические функции f1(})-ИЛИ и f2(})-ИЛИ, в которых функциональные выходные связи являются функциональными выходными связями структуры условной «i» зоны минимизации для формирования аргумента переноса (q
j+1)i и (q
j)i, отличающаяся тем, что функциональные структуры последовательных сквозных переносов fj+1(←←)+ и fj(←←)+ условно «i» «Зоны формирования» для «j+1» разряда и «j» разряда выполнены в виде функционально независимых структур, в которые введены логические функции f1(
&
)-НЕ, f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ и f2(
&
)-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ соответственно, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида
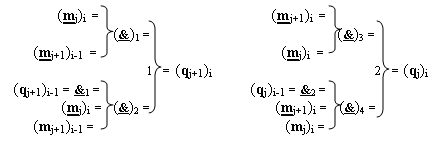
где 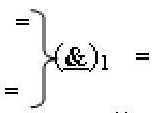 - логическая функция f1(}&
)-ИЛИ-НЕ.
- логическая функция f1(}&
)-ИЛИ-НЕ.
| УЭЙКЕРЛИ Д | |||
| Проектирование цифровых устройств | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Блок формирования сквозного переноса в сумматоре | 1984 |
|
SU1196852A1 |
| Устройство для формирования сигнала переноса при суммировании многофазных кодов | 1989 |
|
SU1633393A1 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА С ПРЕДВАРИТЕЛЬНО ВВОДИМЫМИ ПЕРЕНОСАМИ (ВАРИАНТЫ) | 2008 |
|
RU2381545C2 |
| JP 2002312160 A, 25.10.2002 | |||
| US 5600583 A, 04.02.1997. | |||
Авторы
Даты
2011-07-20—Публикация
2010-03-04—Подача