Текст описания приведен в факсимильном виде.







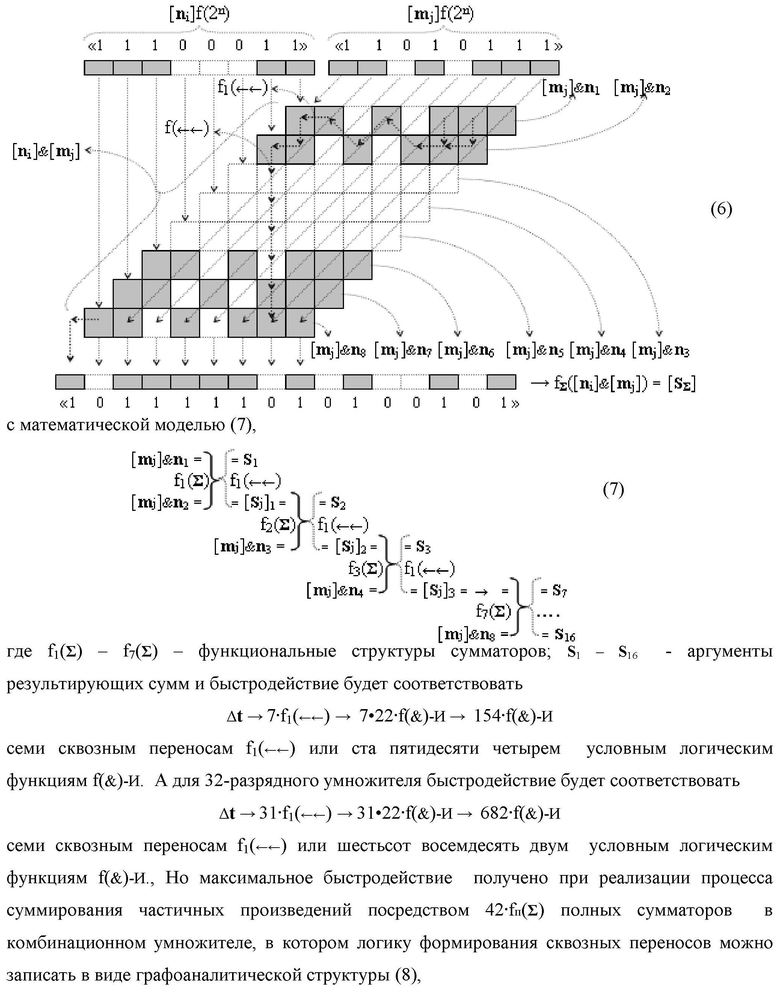

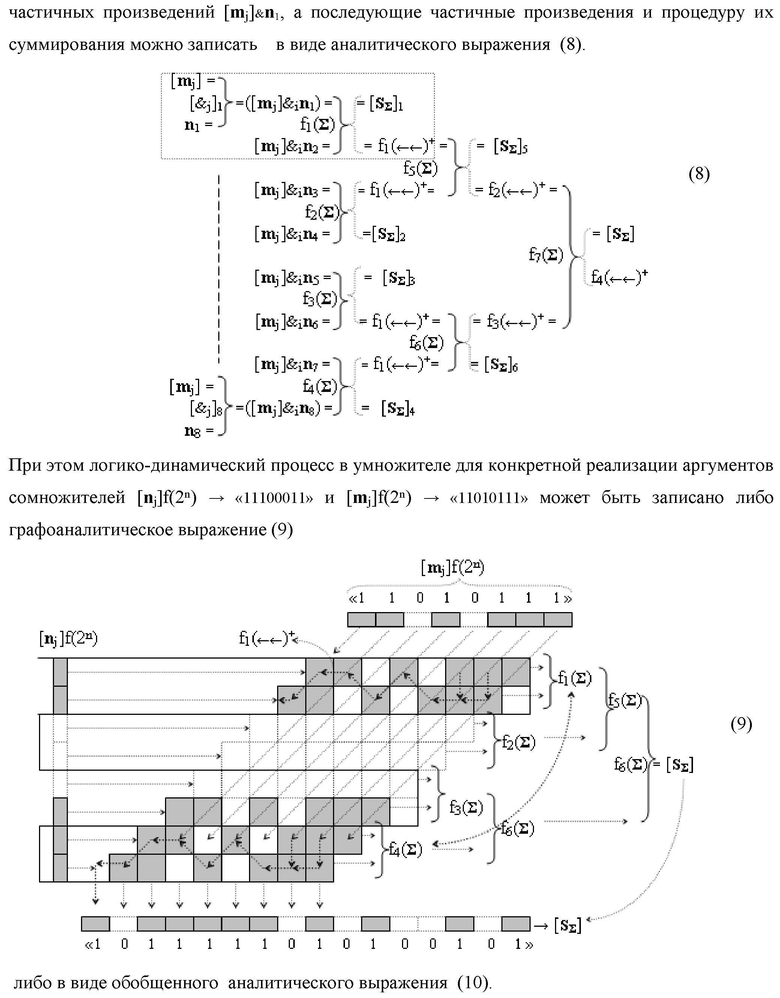



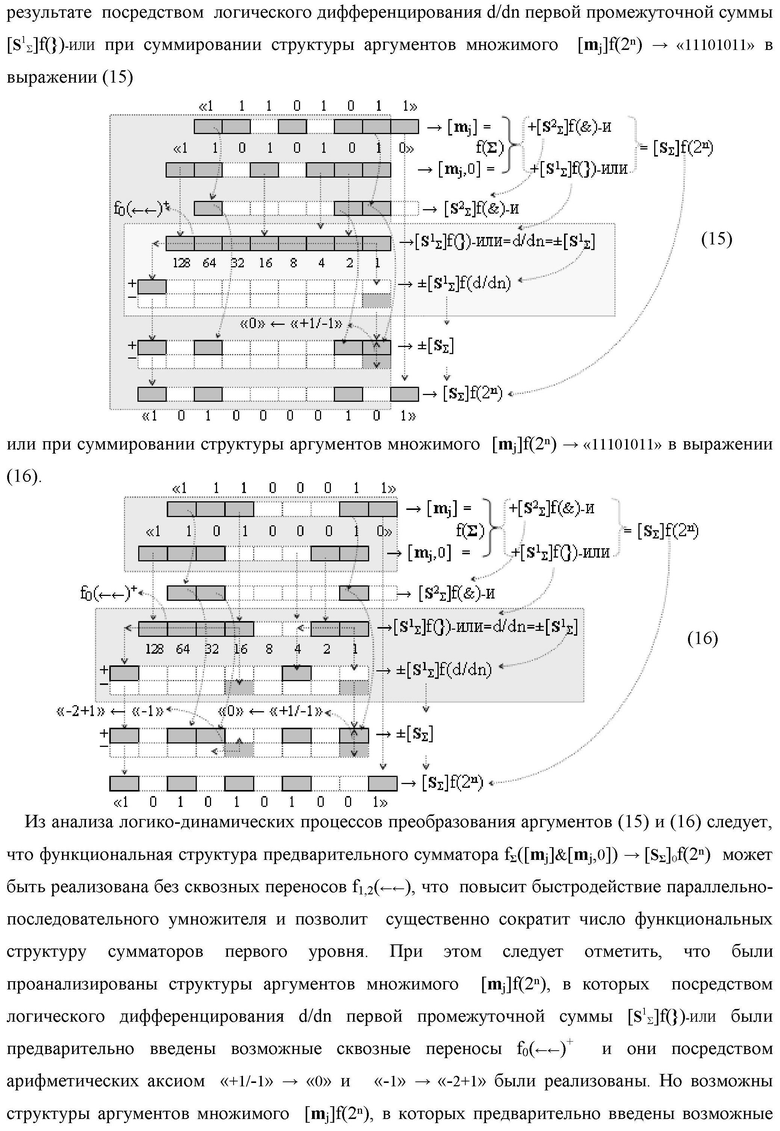
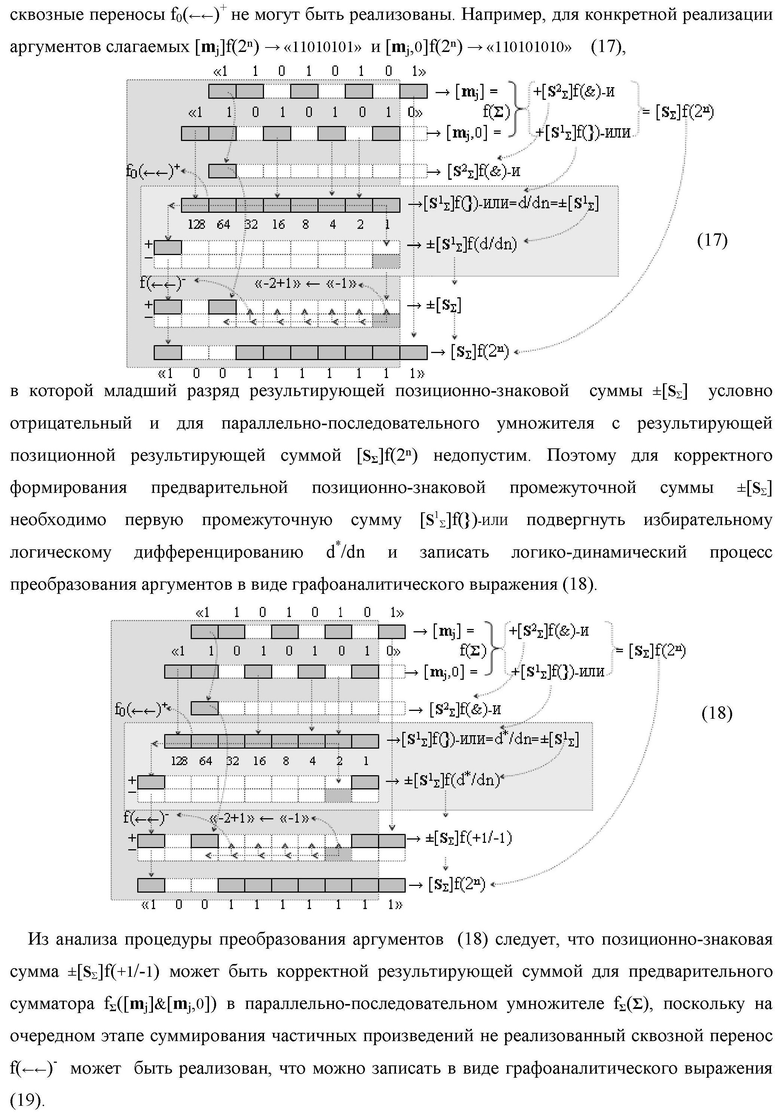
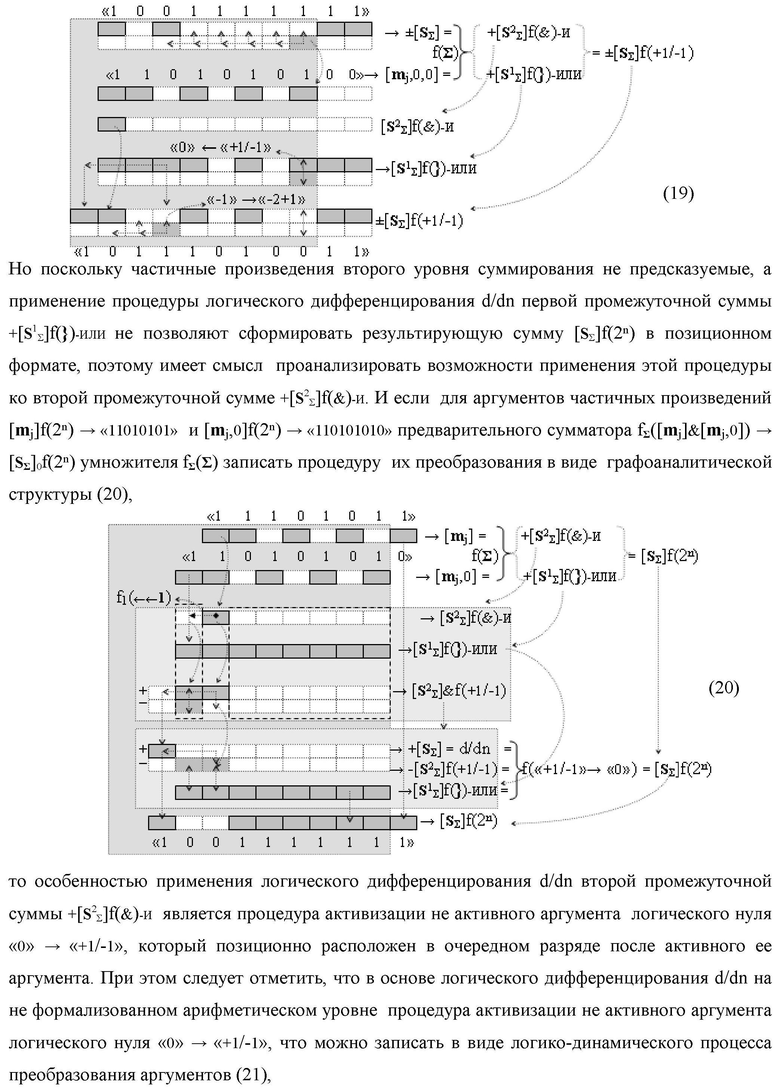

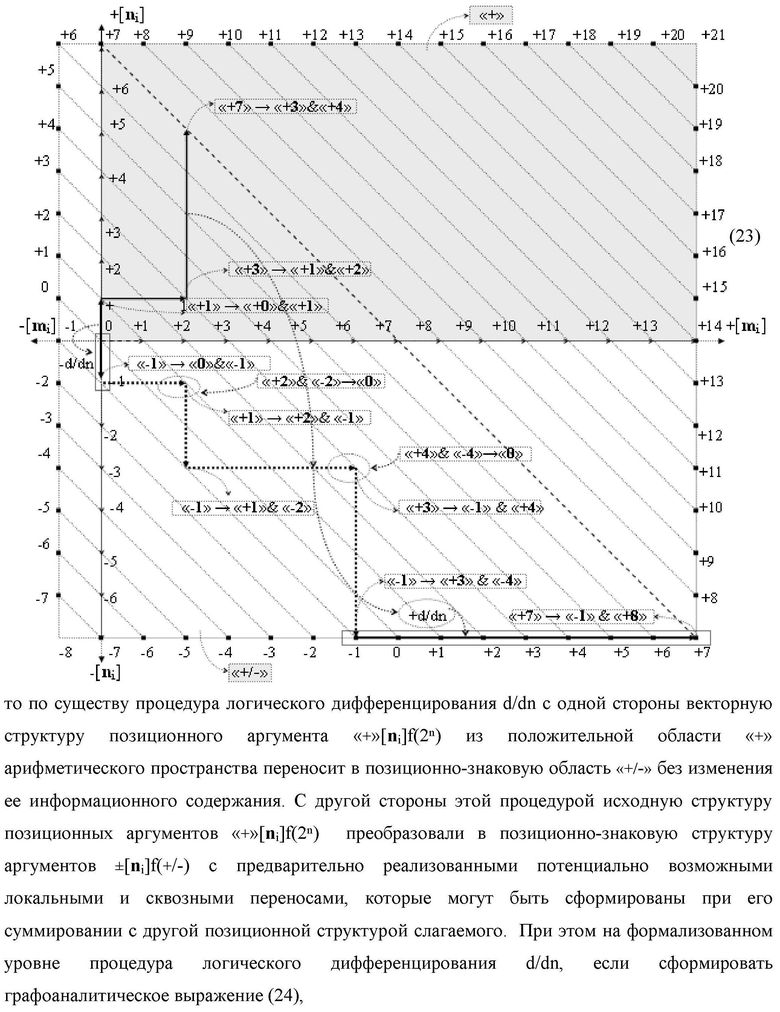



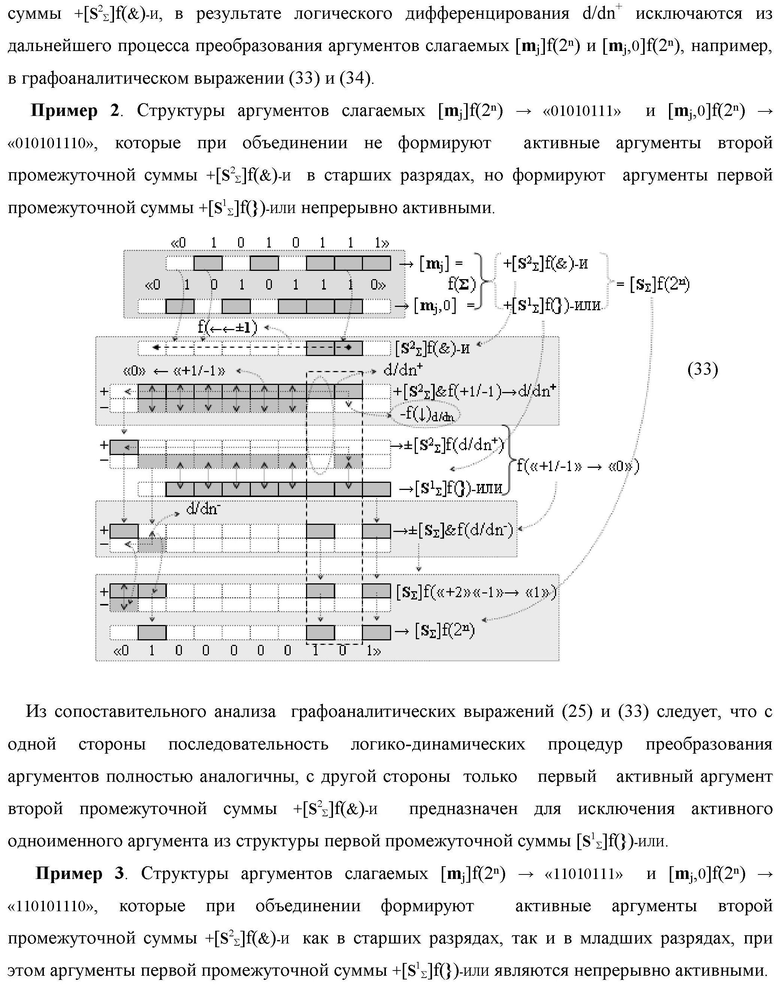


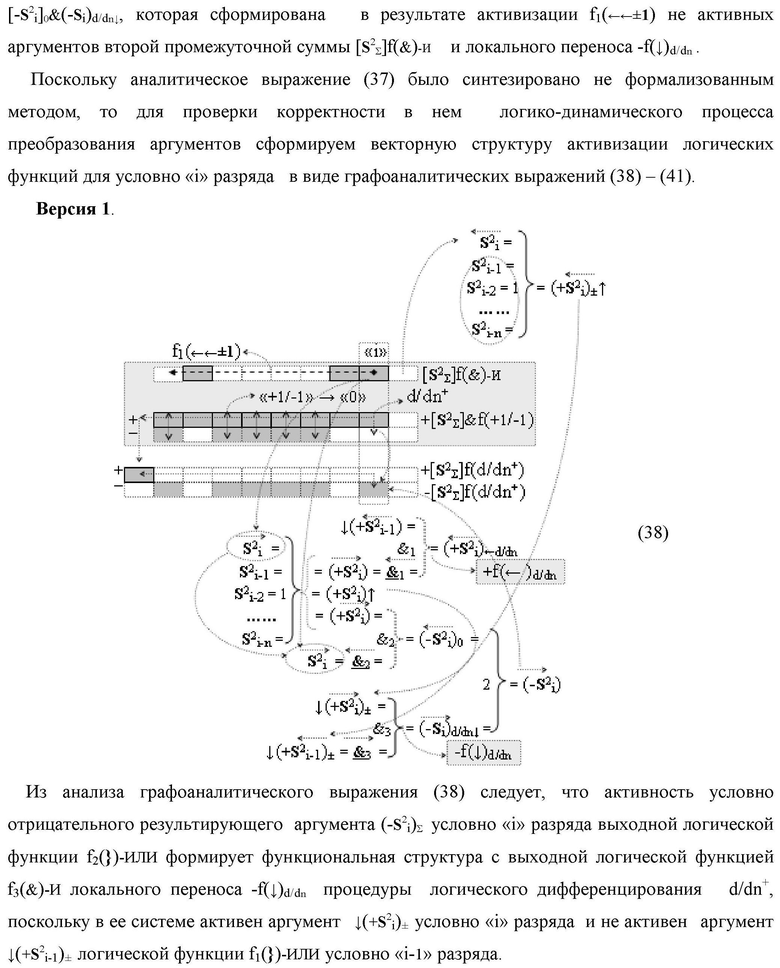




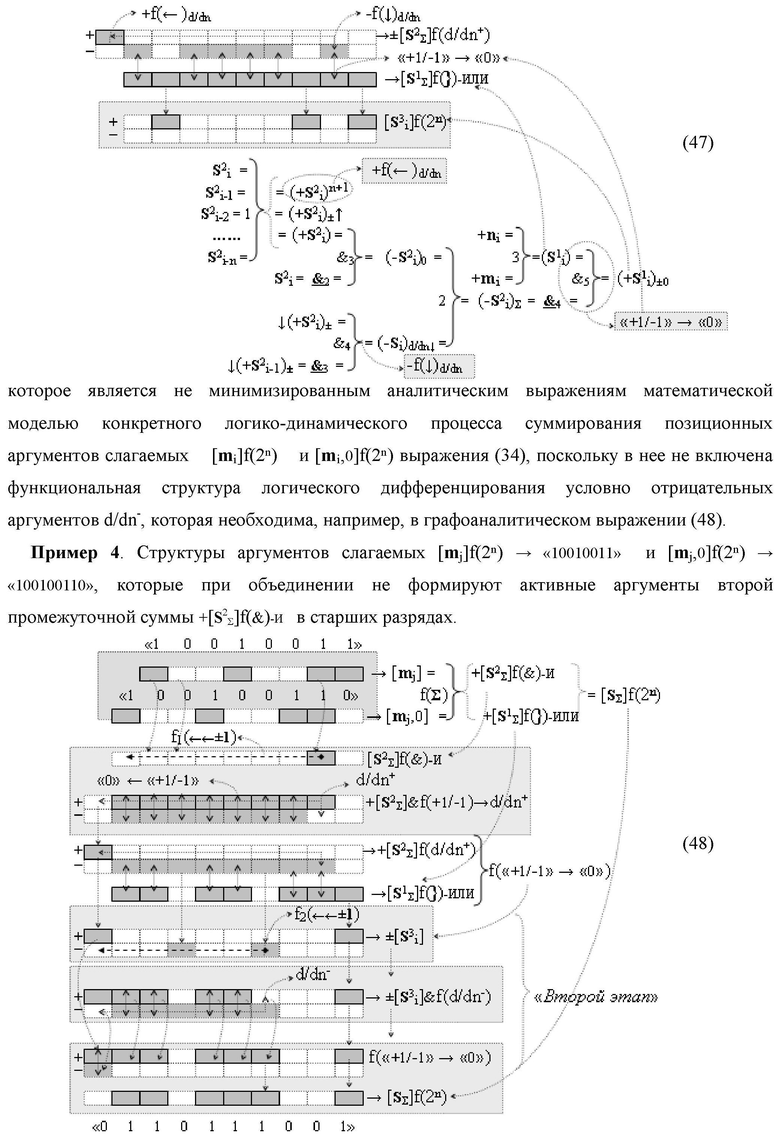

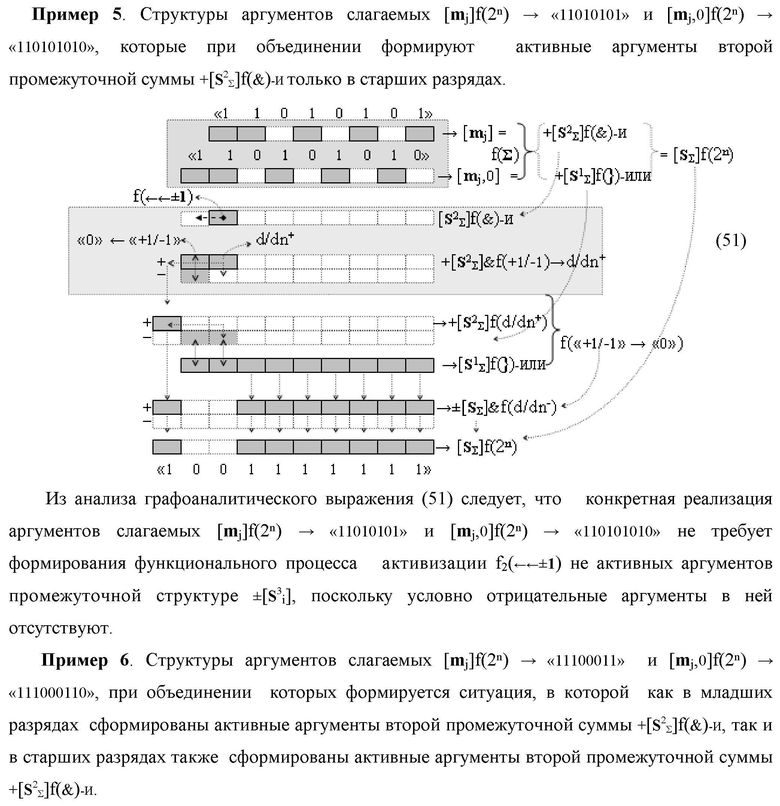
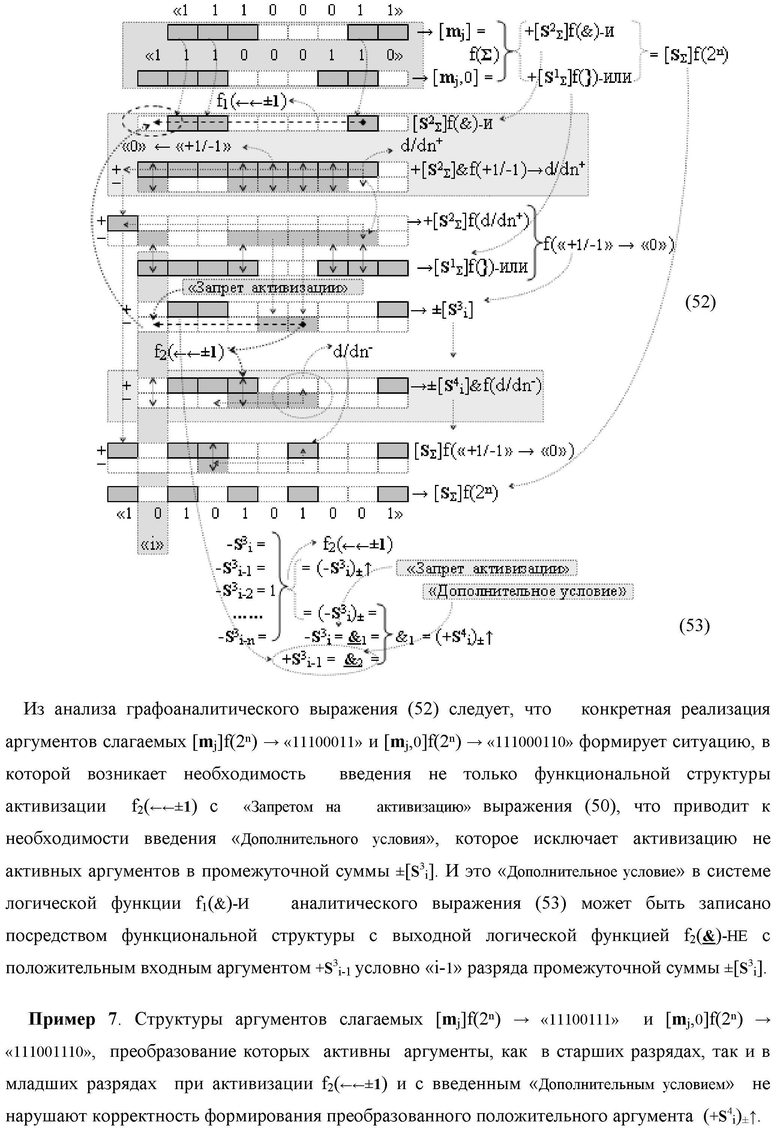
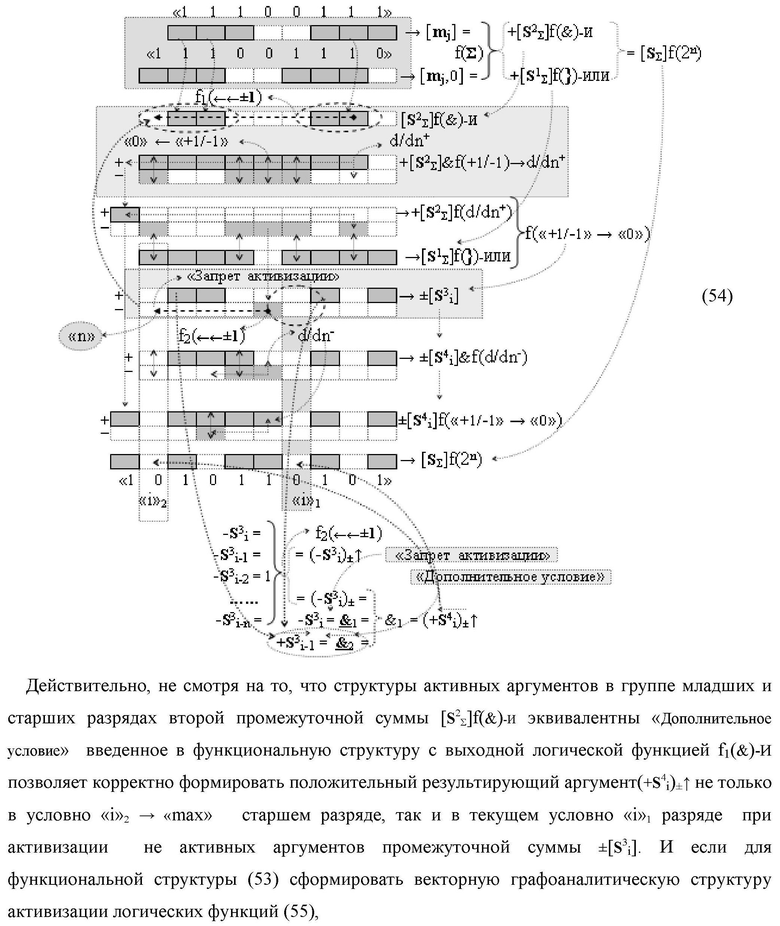
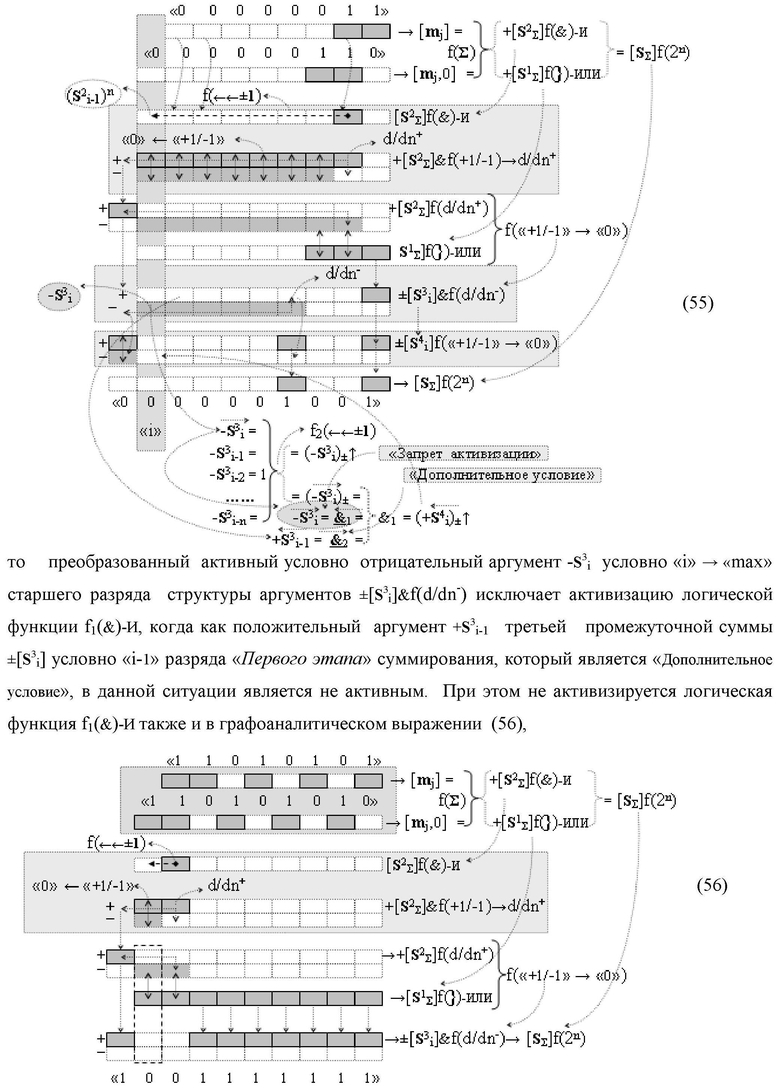
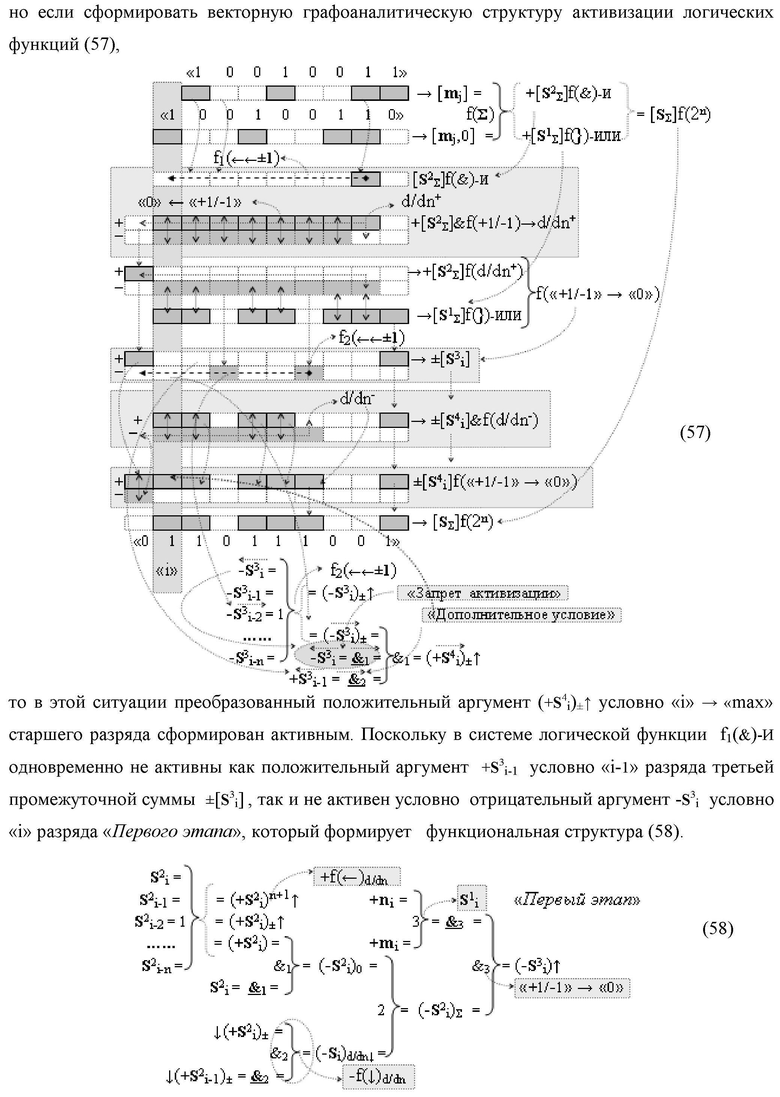


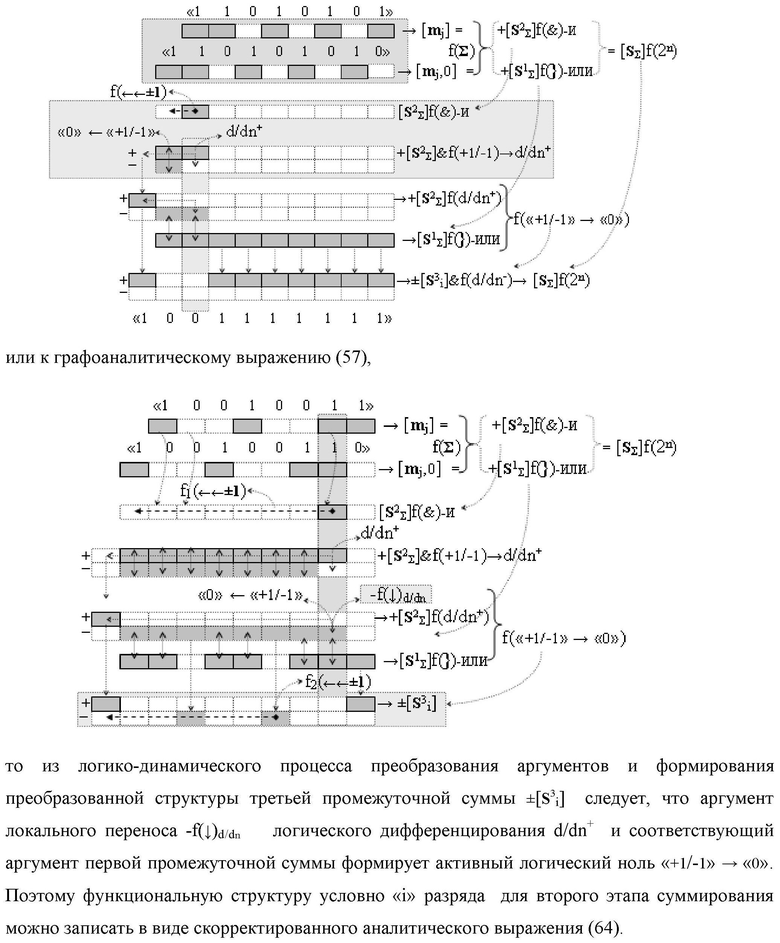






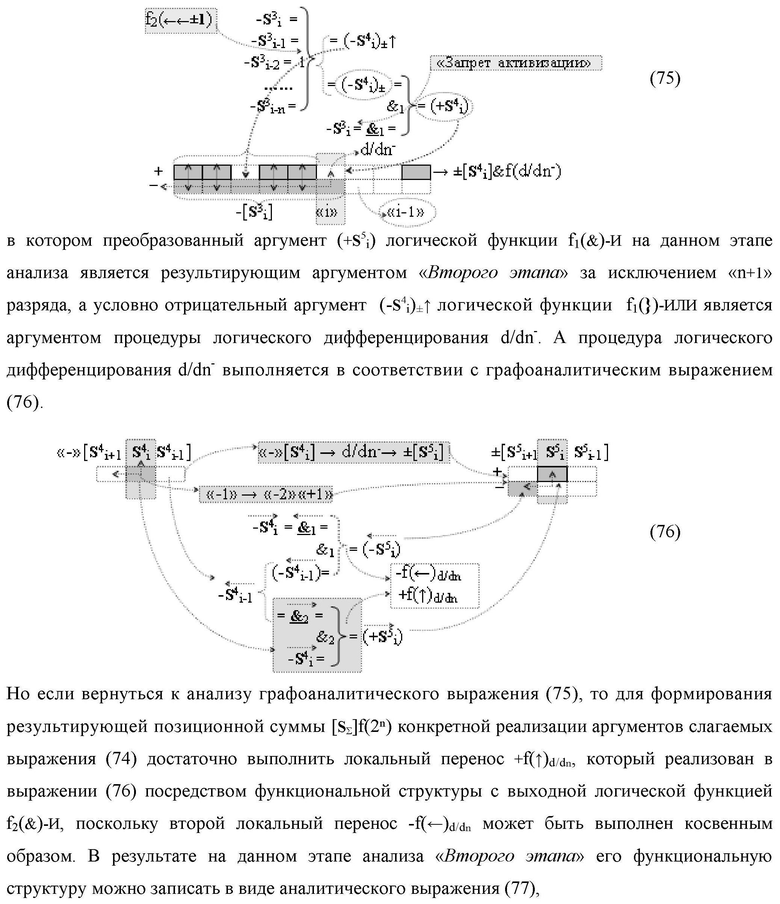
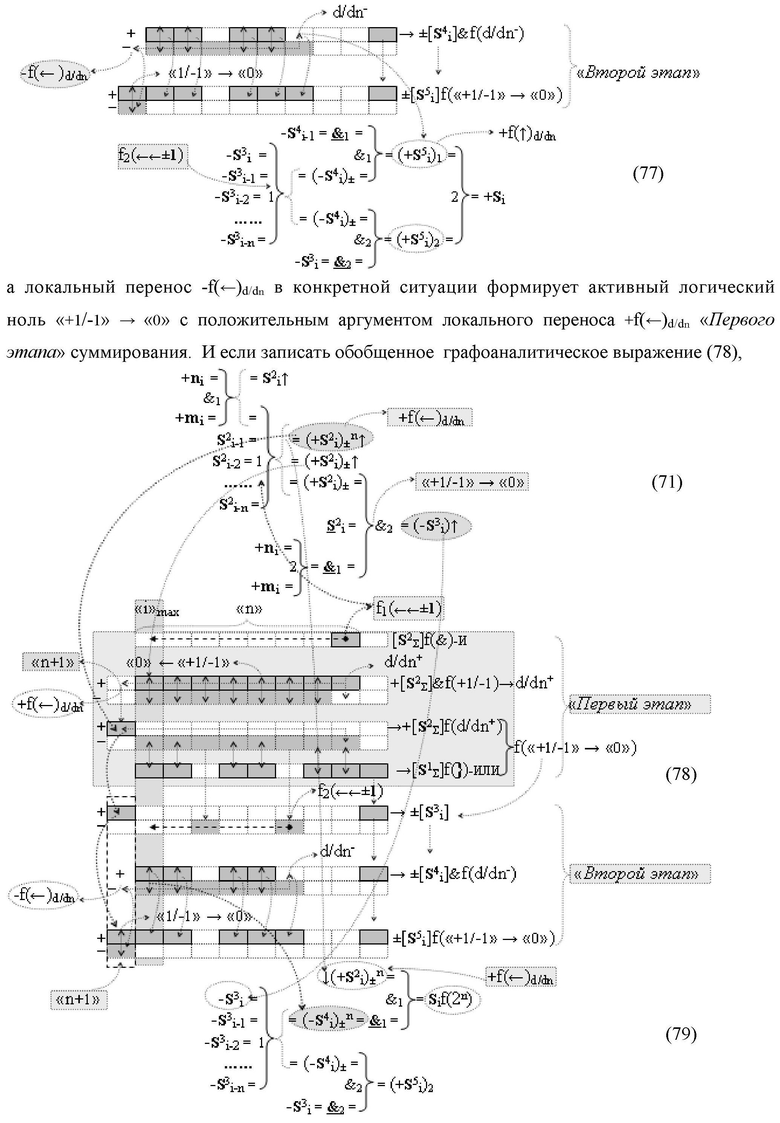
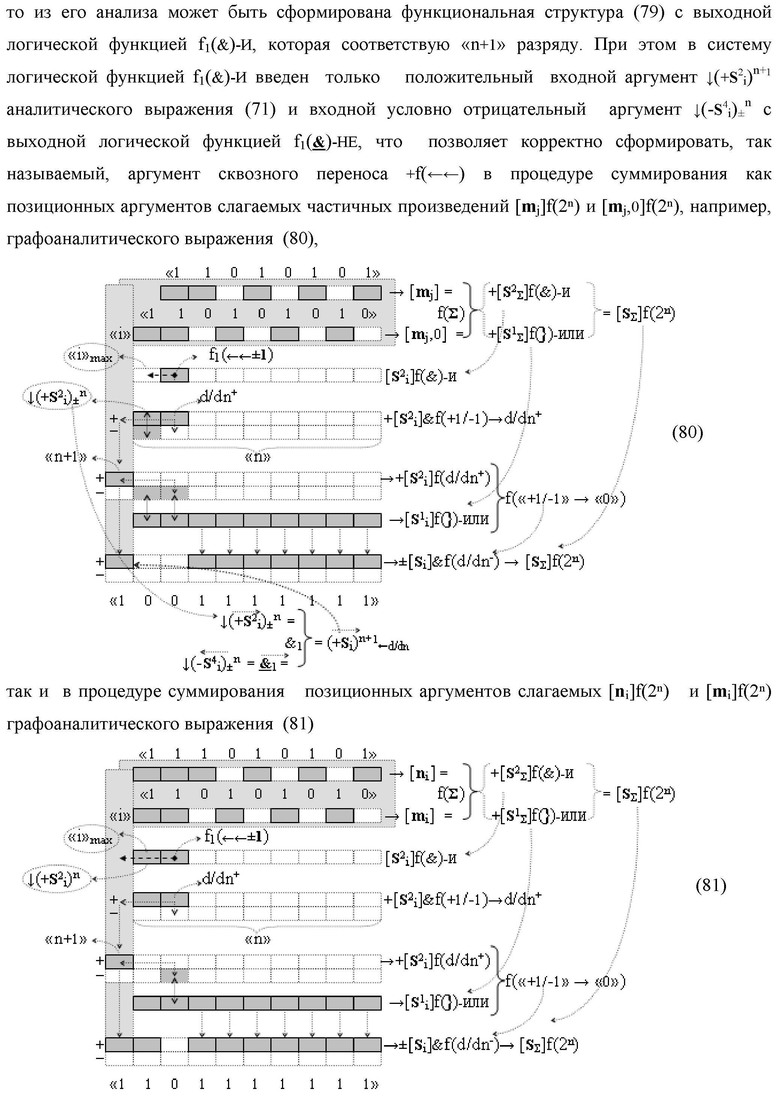

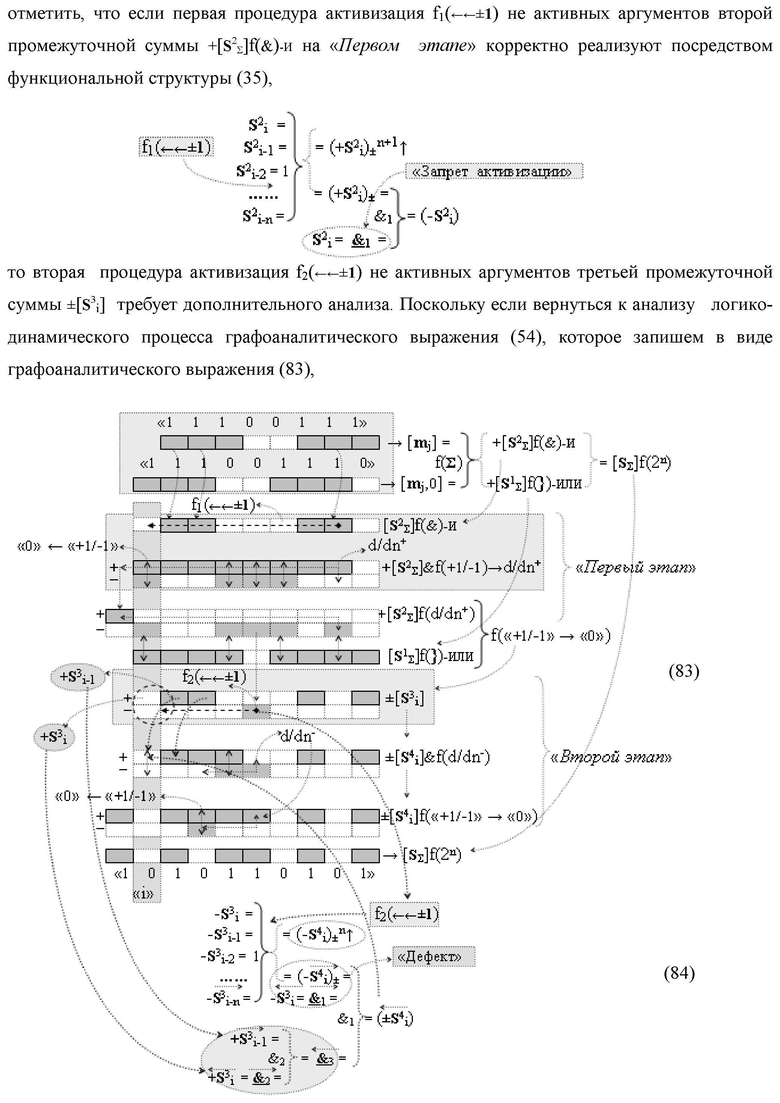


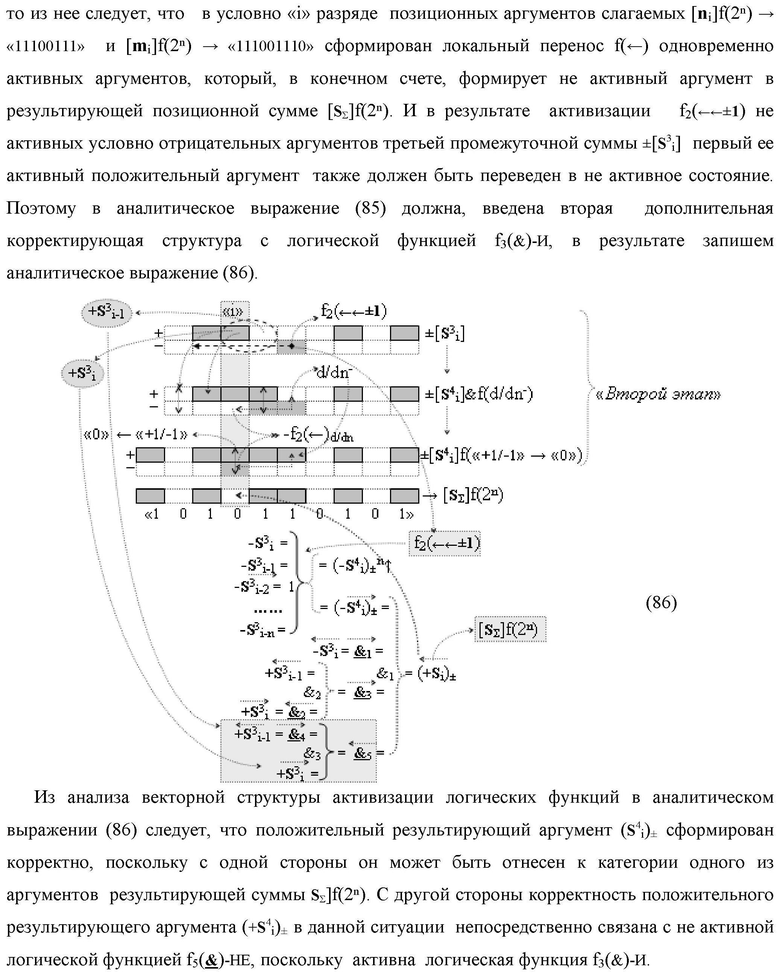
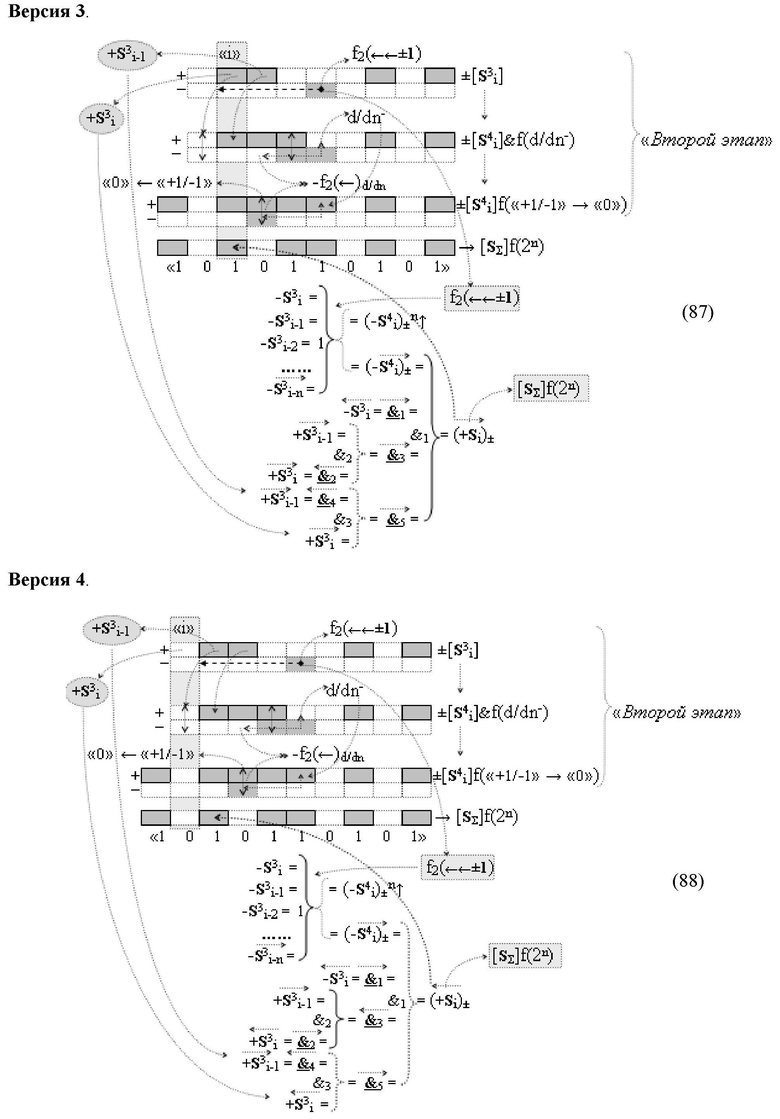
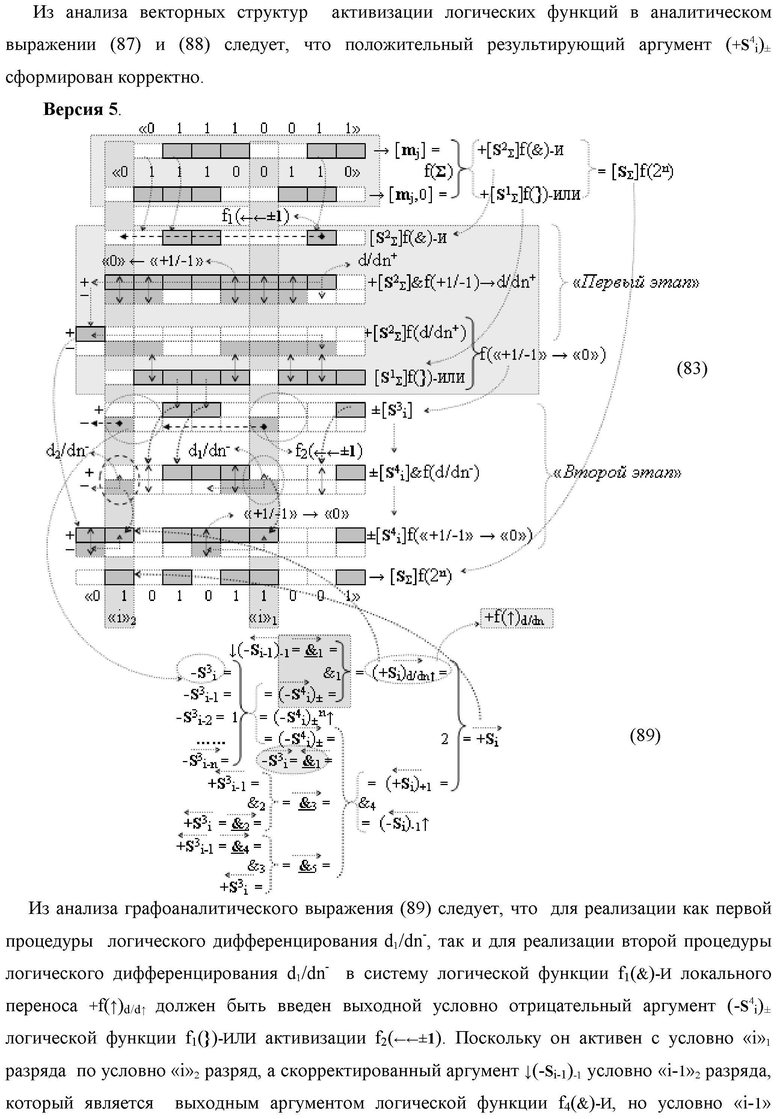

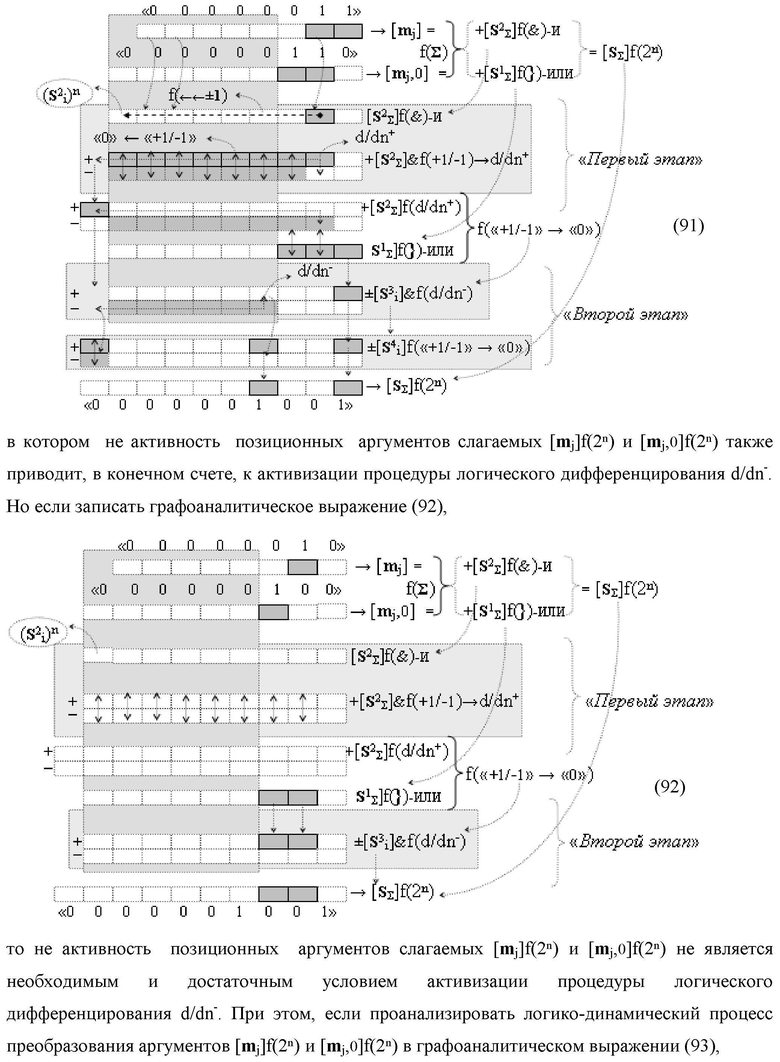

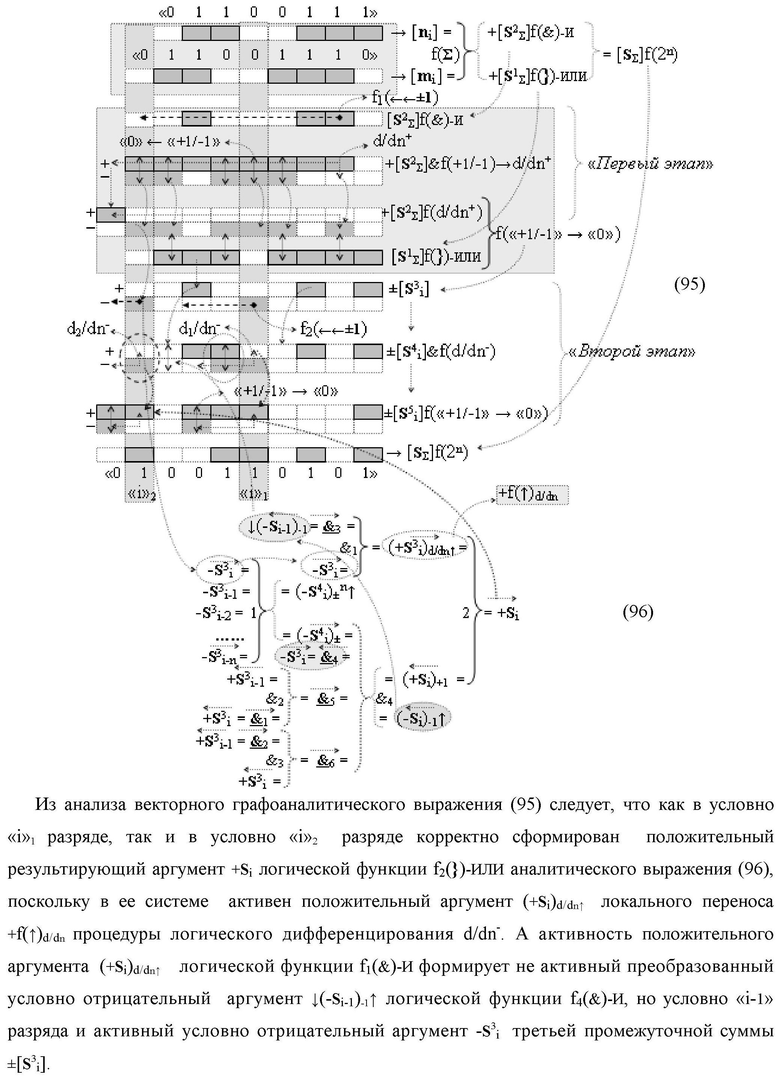




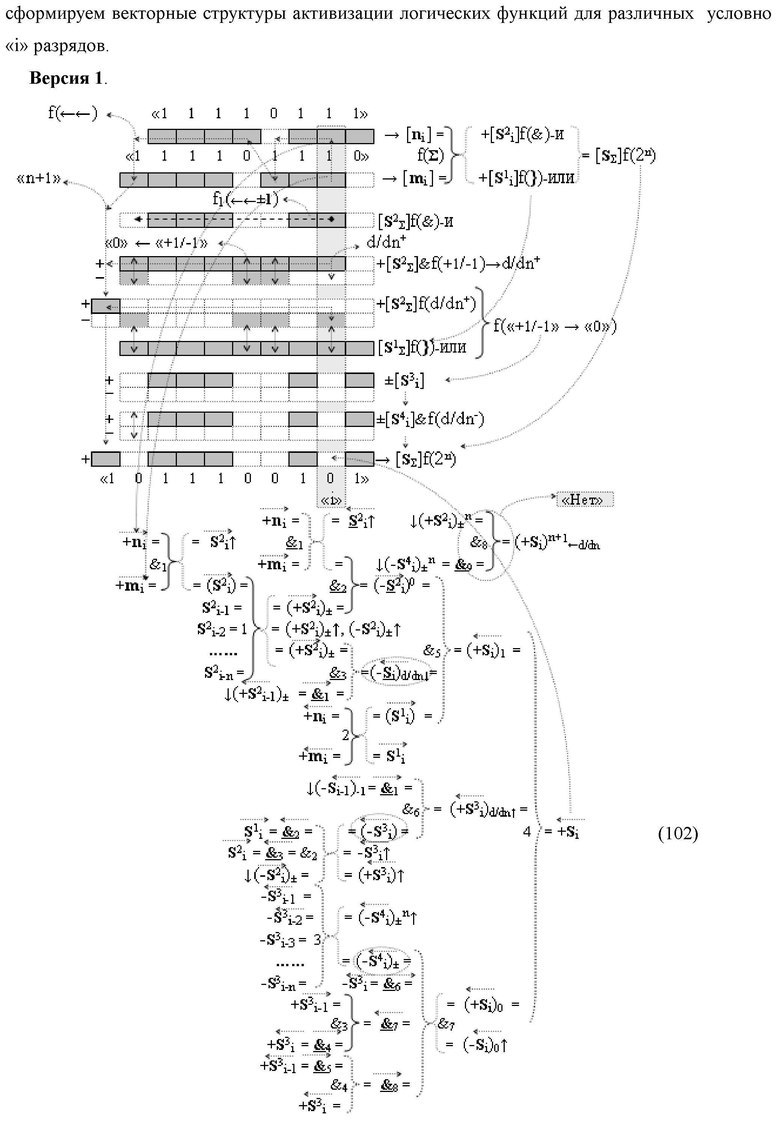
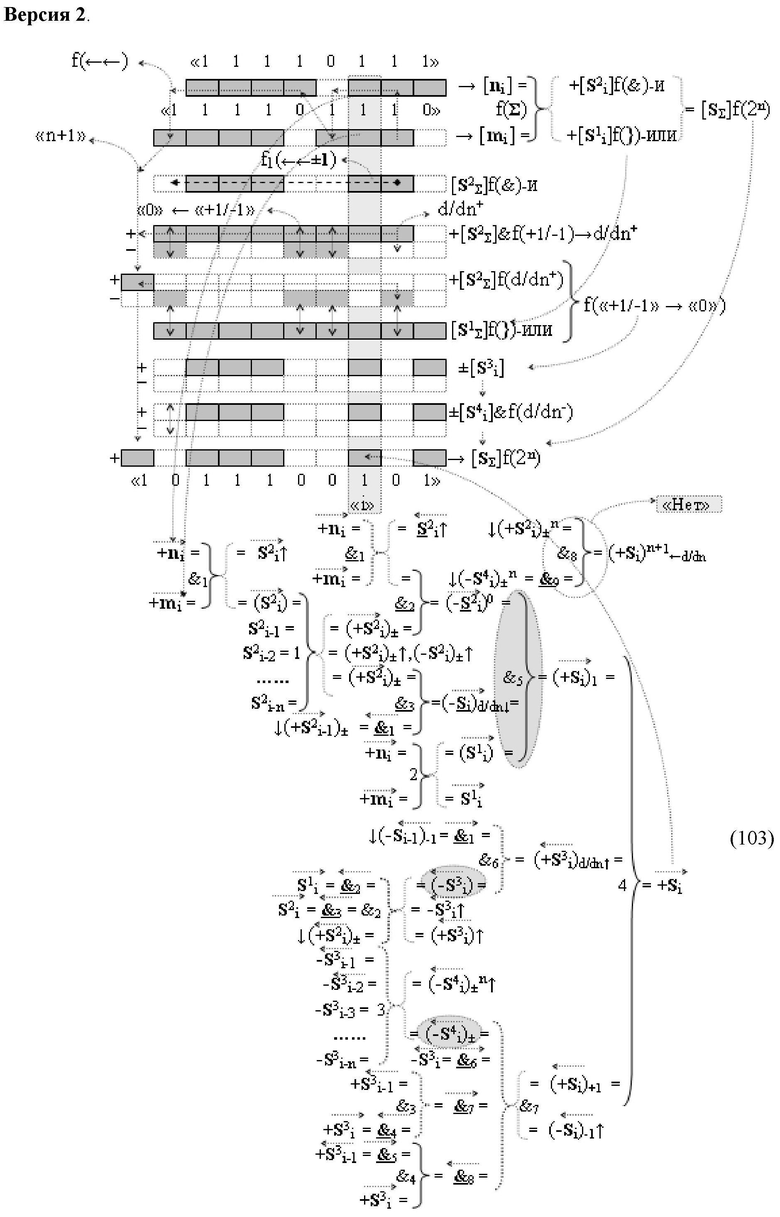
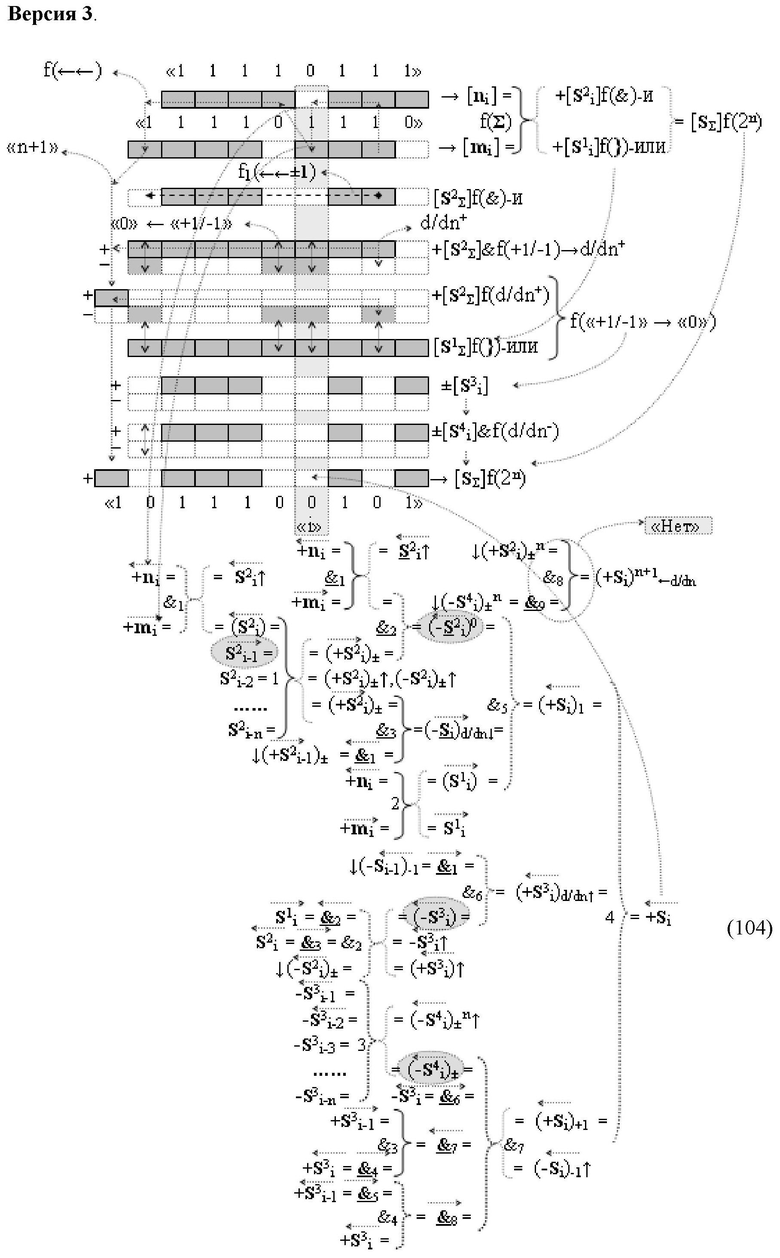

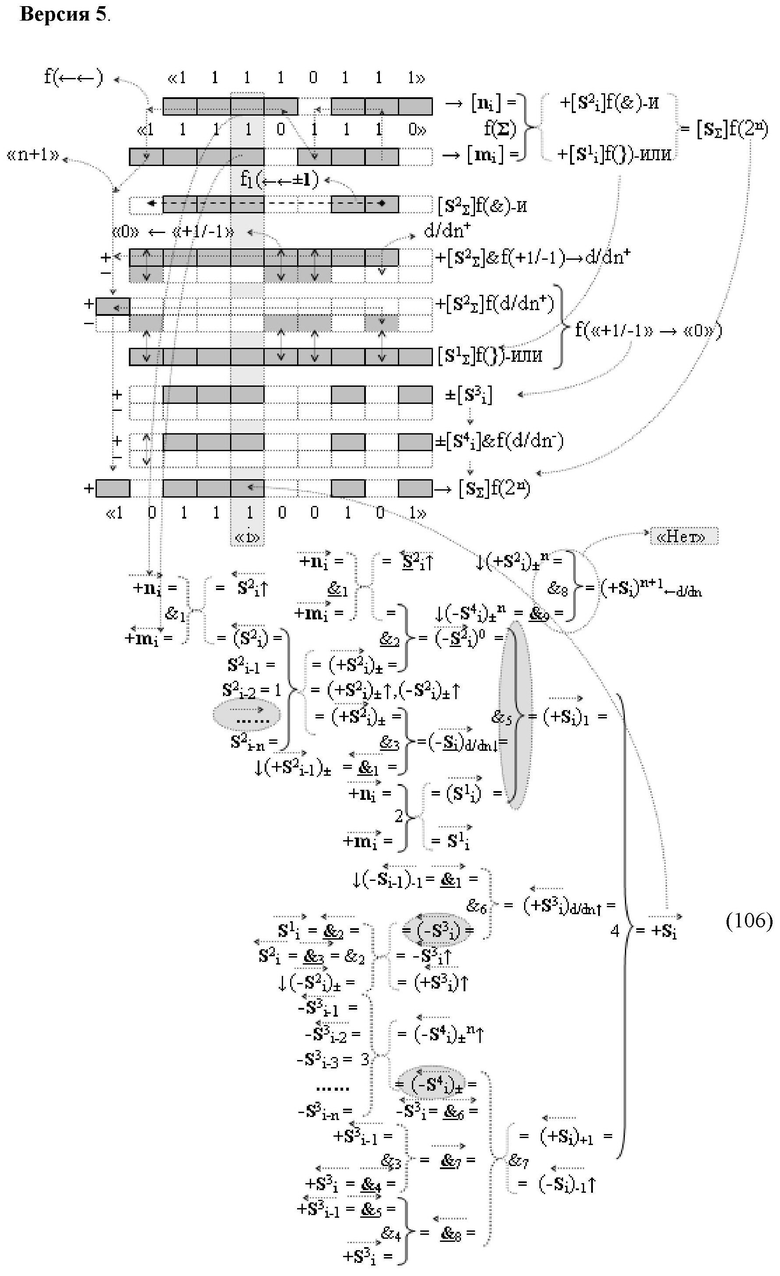
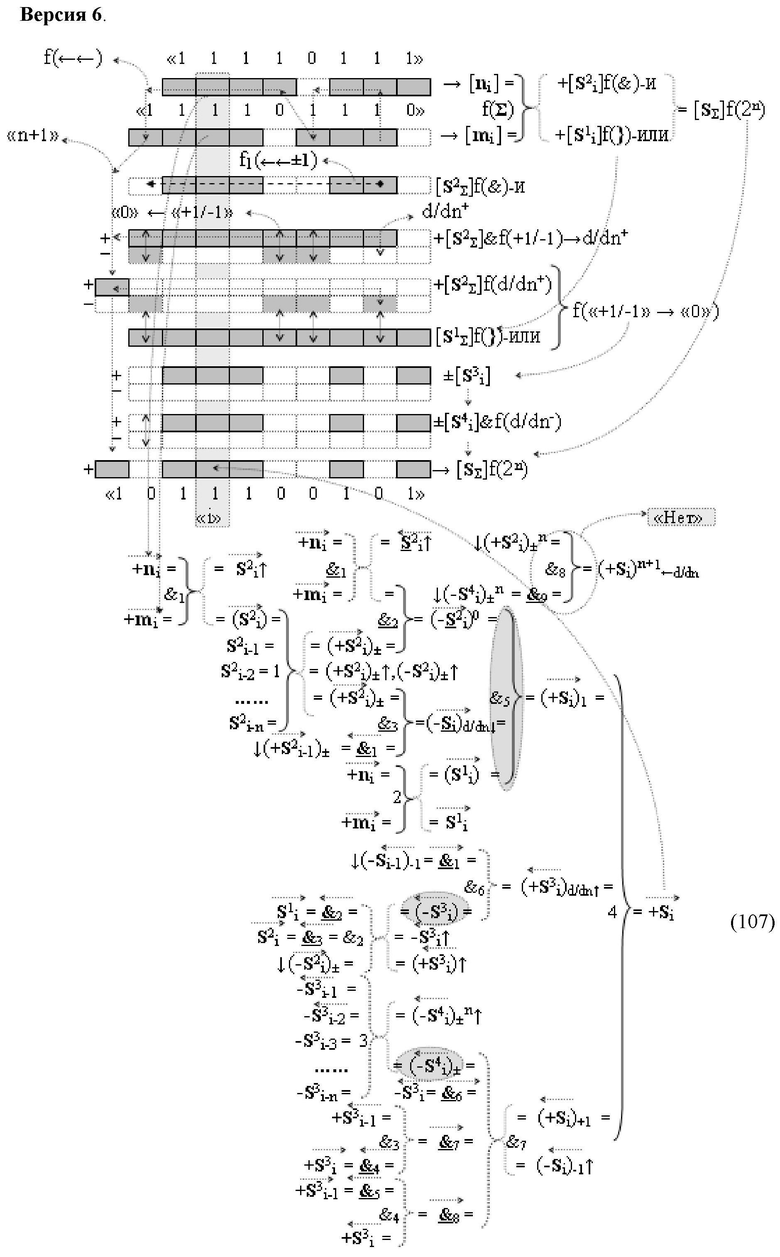
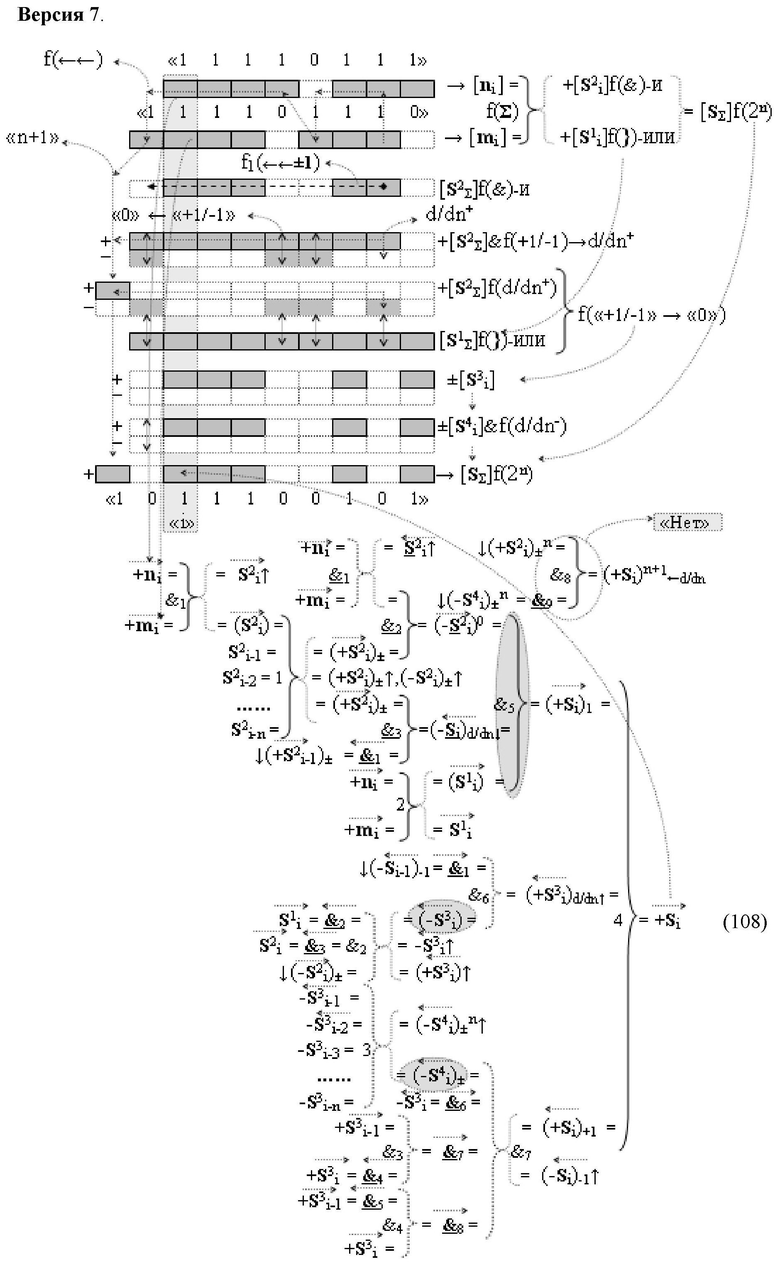
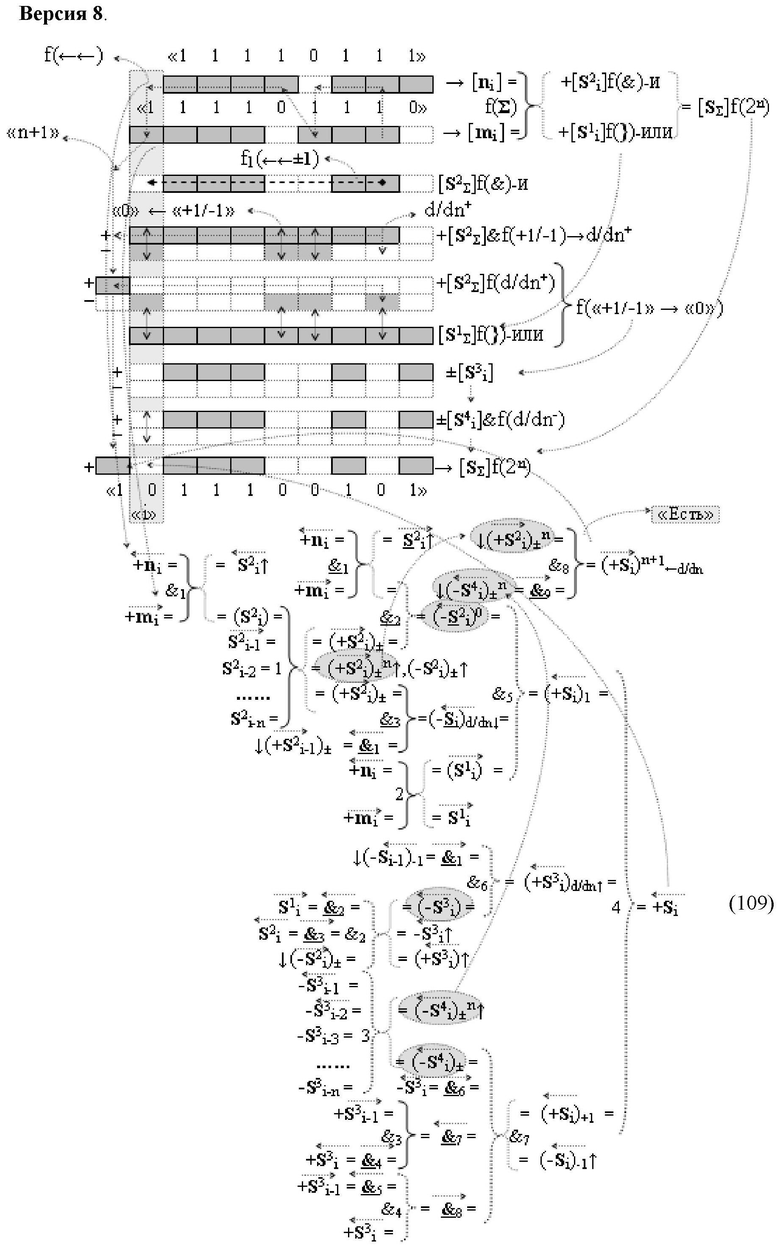
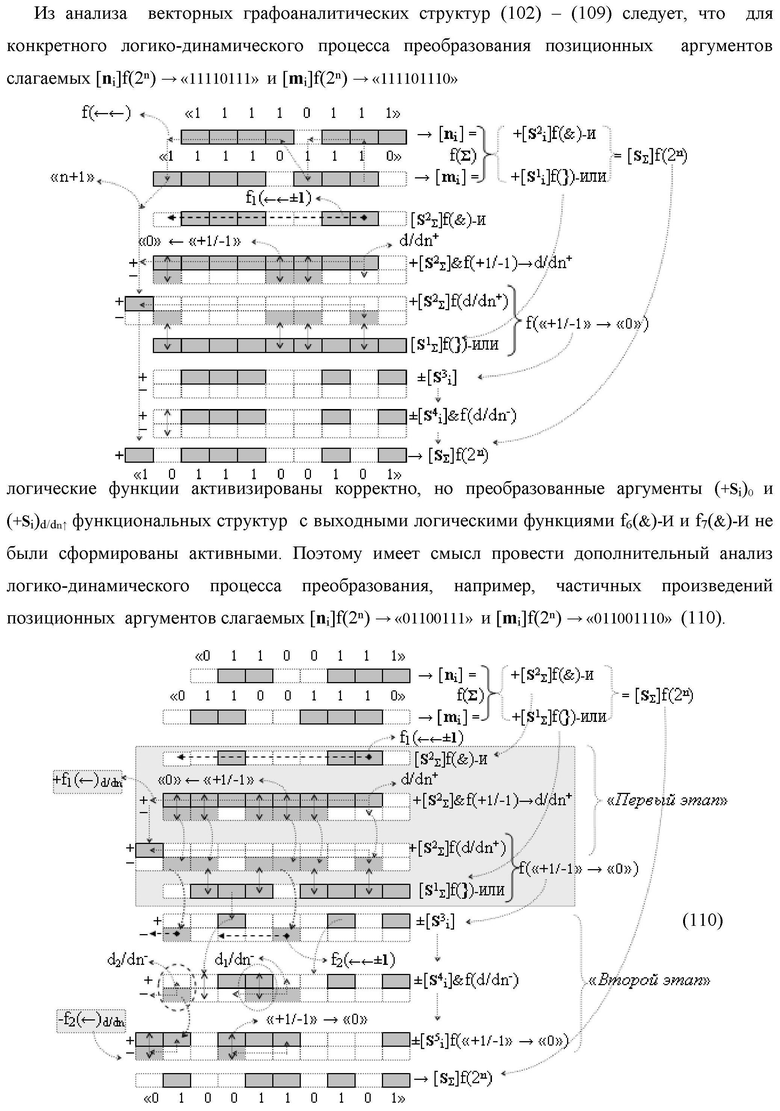
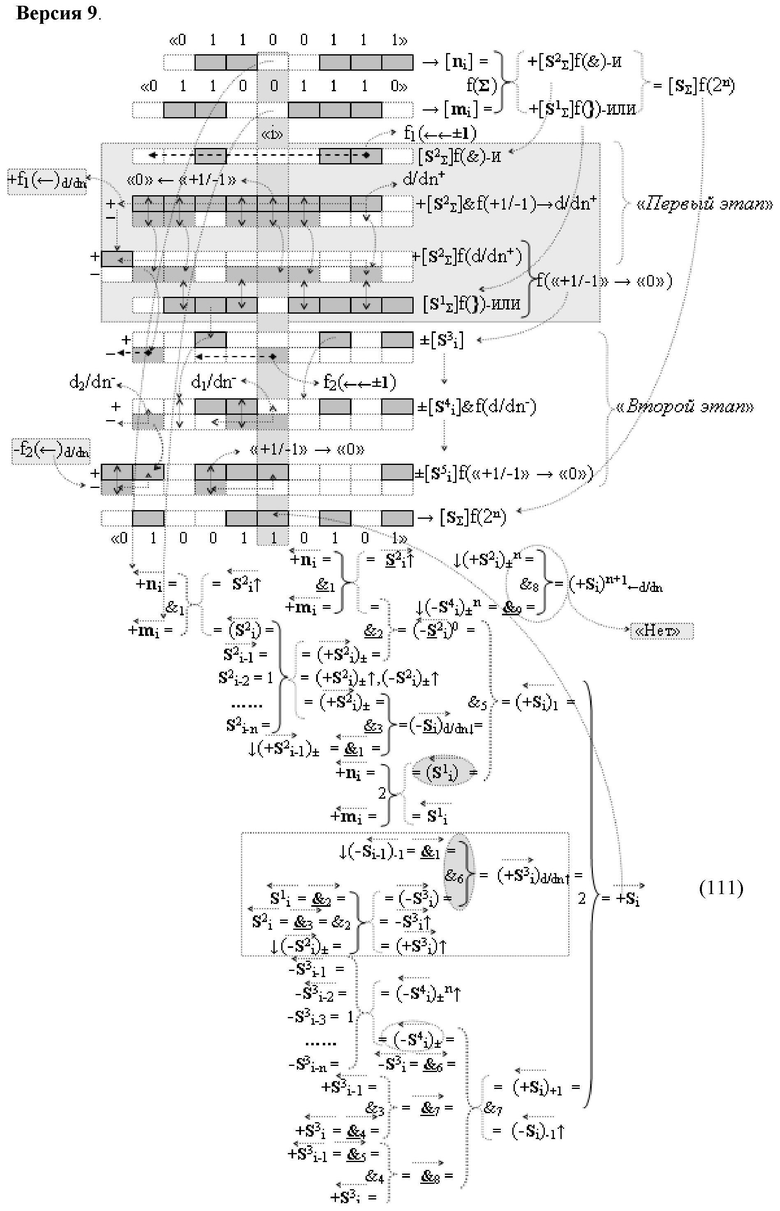
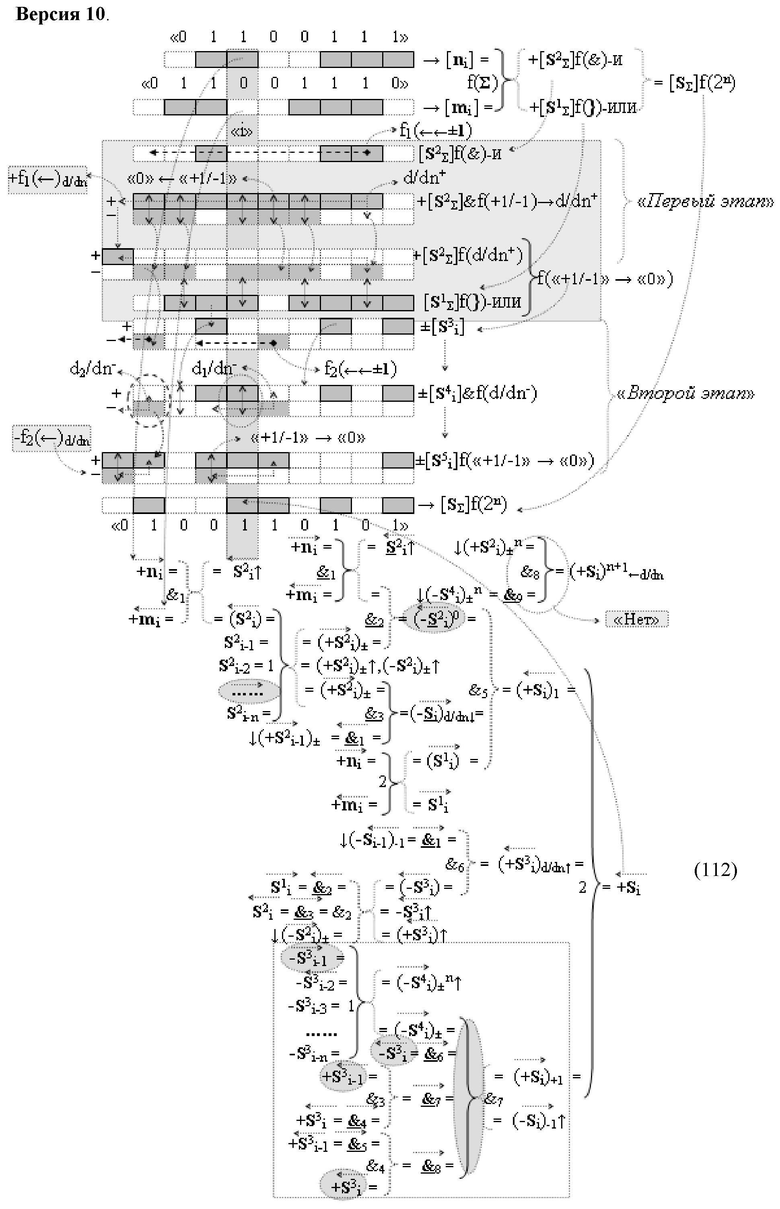
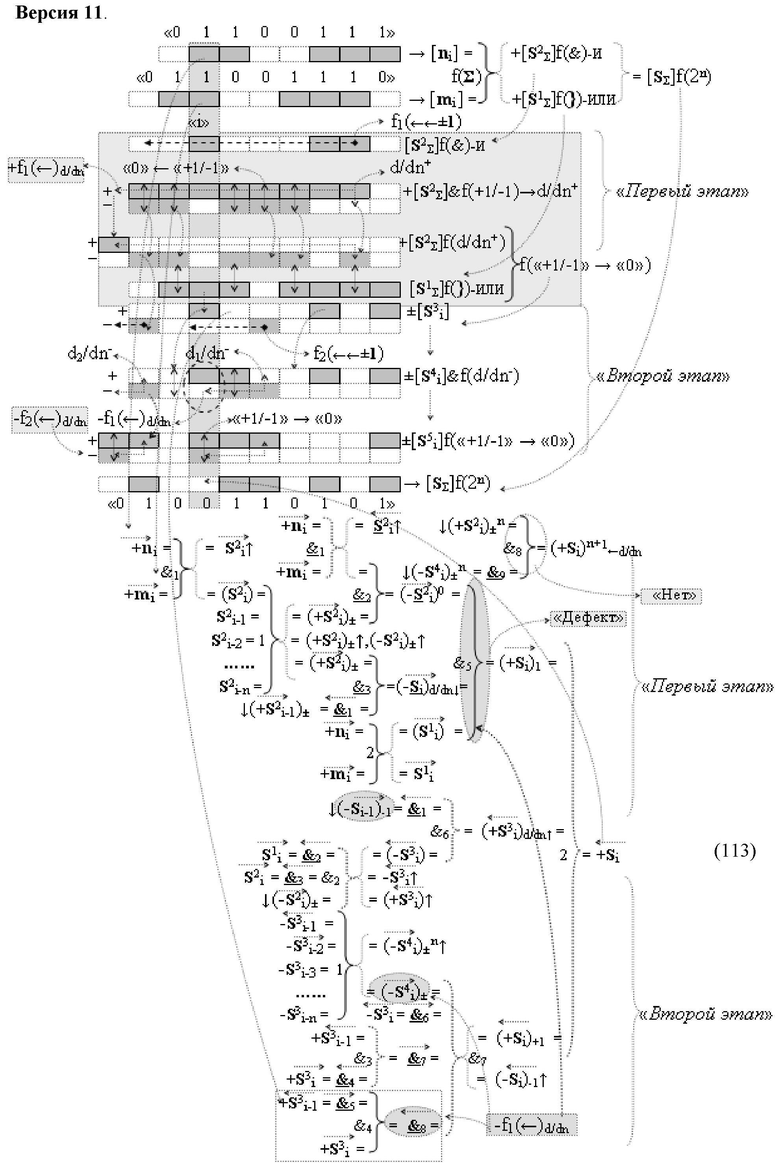
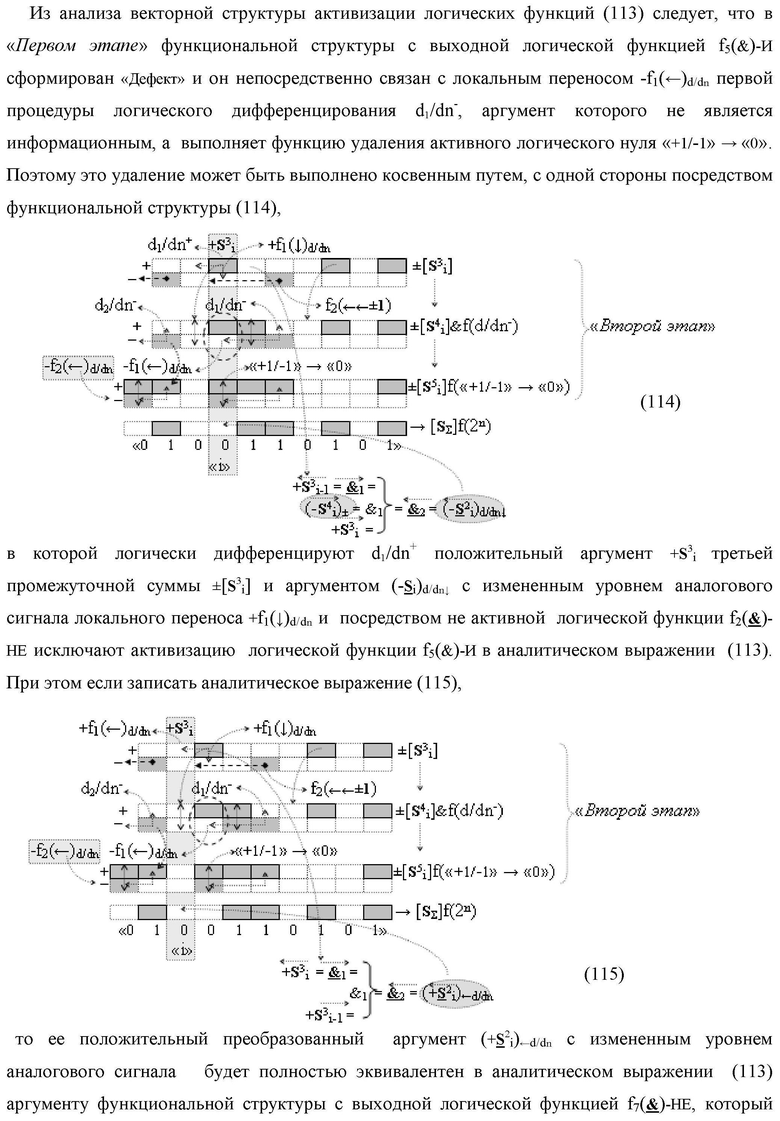



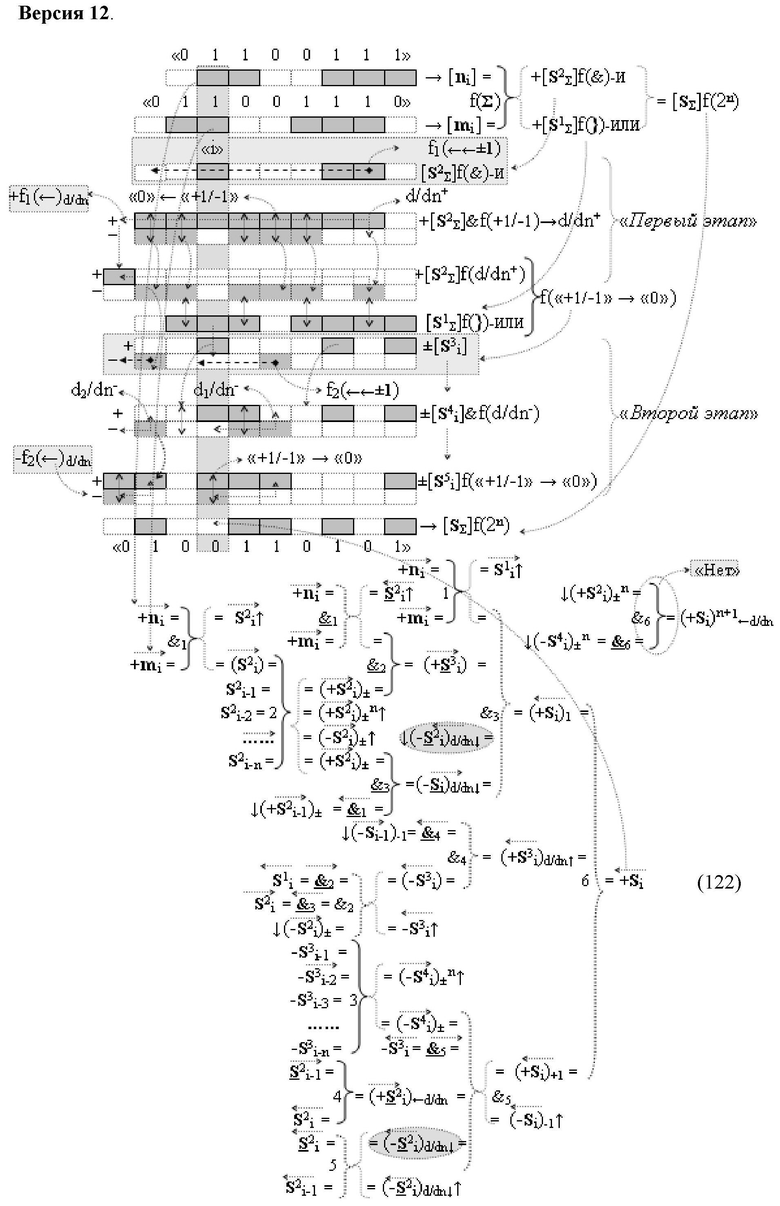
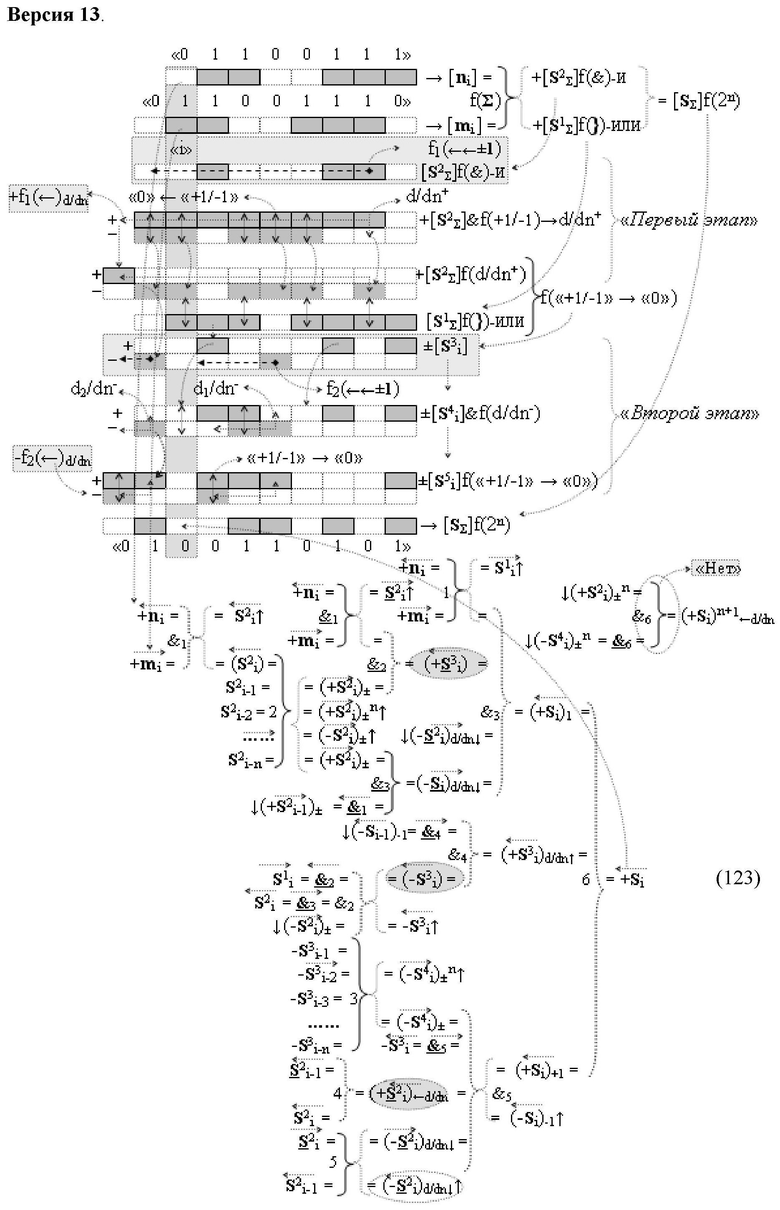
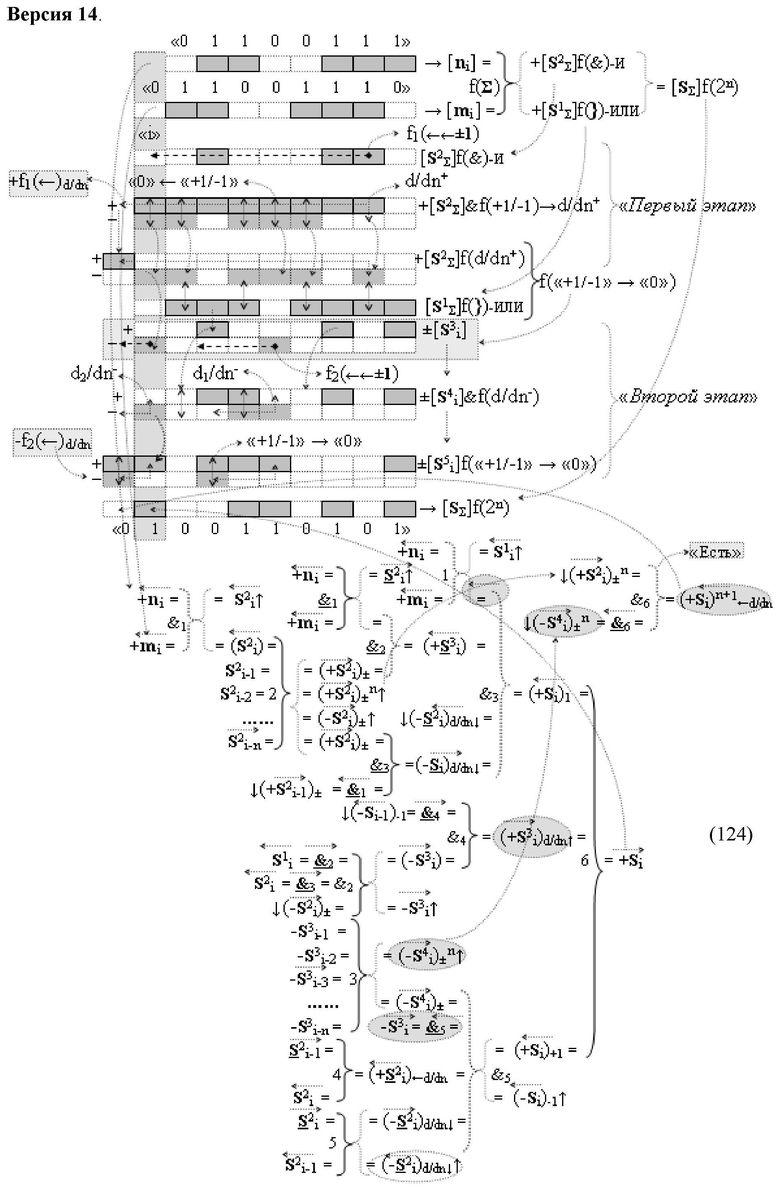




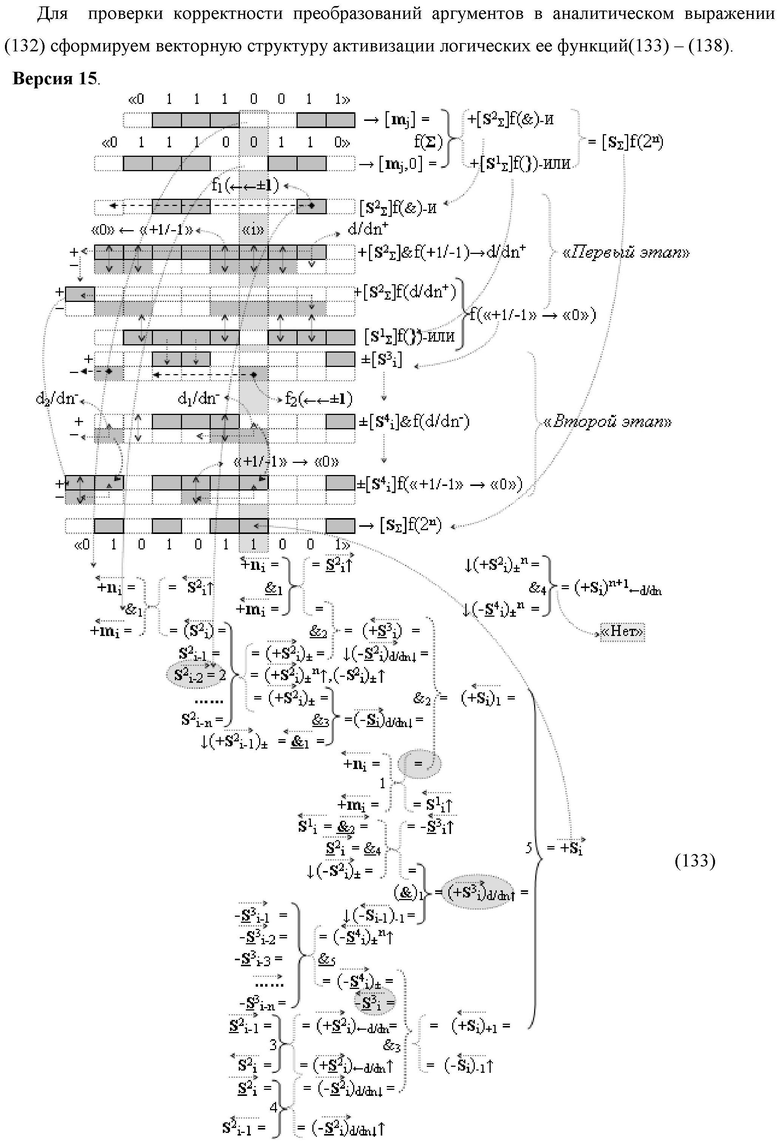
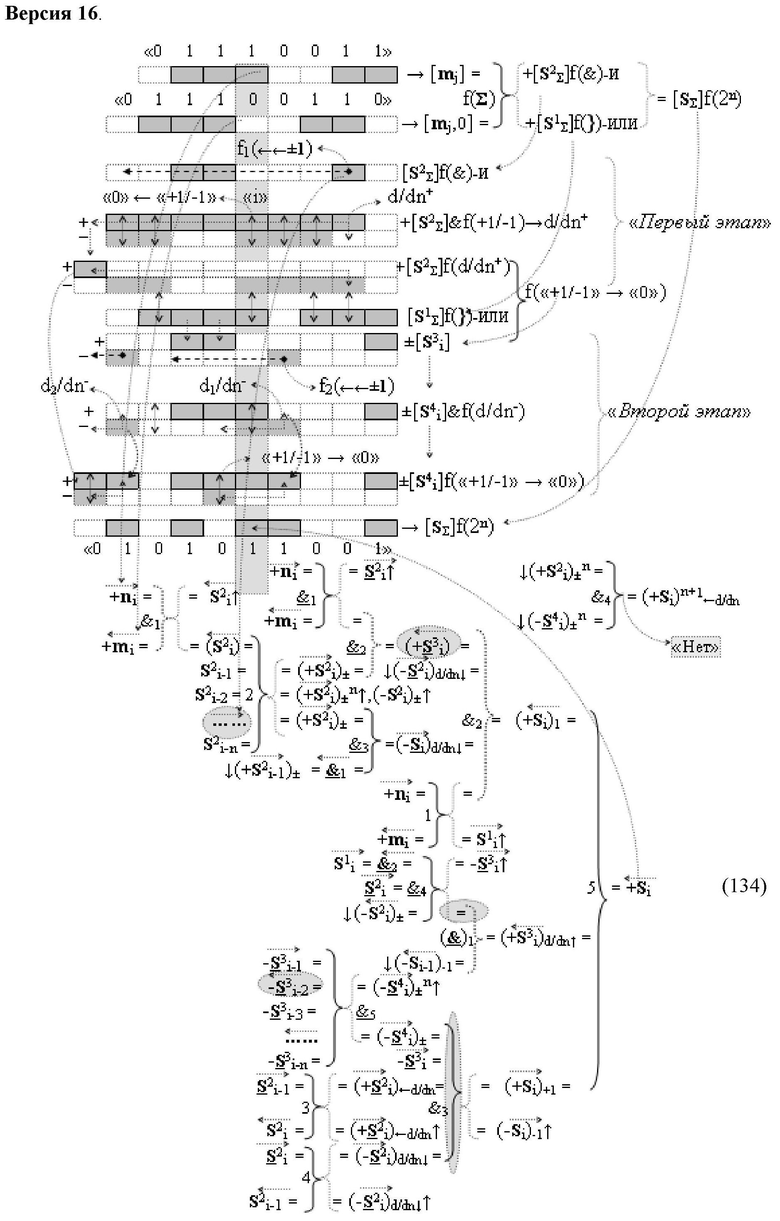
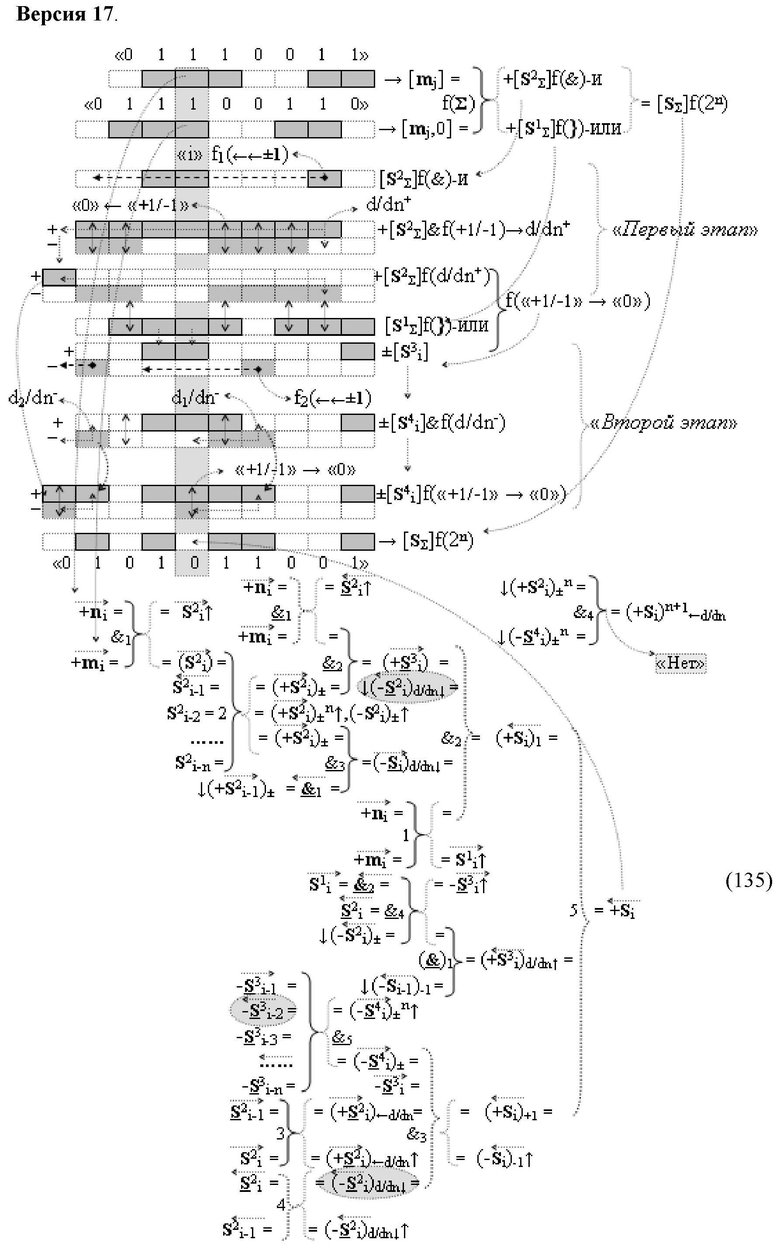
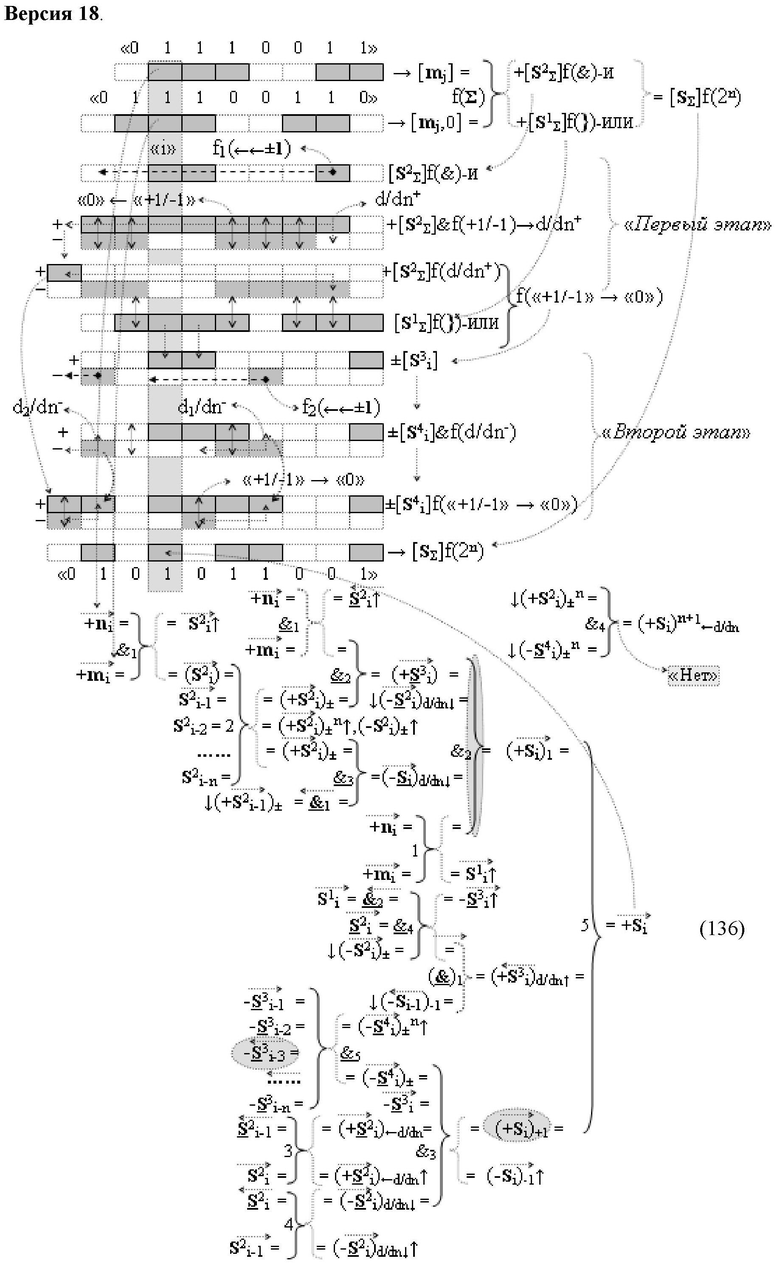
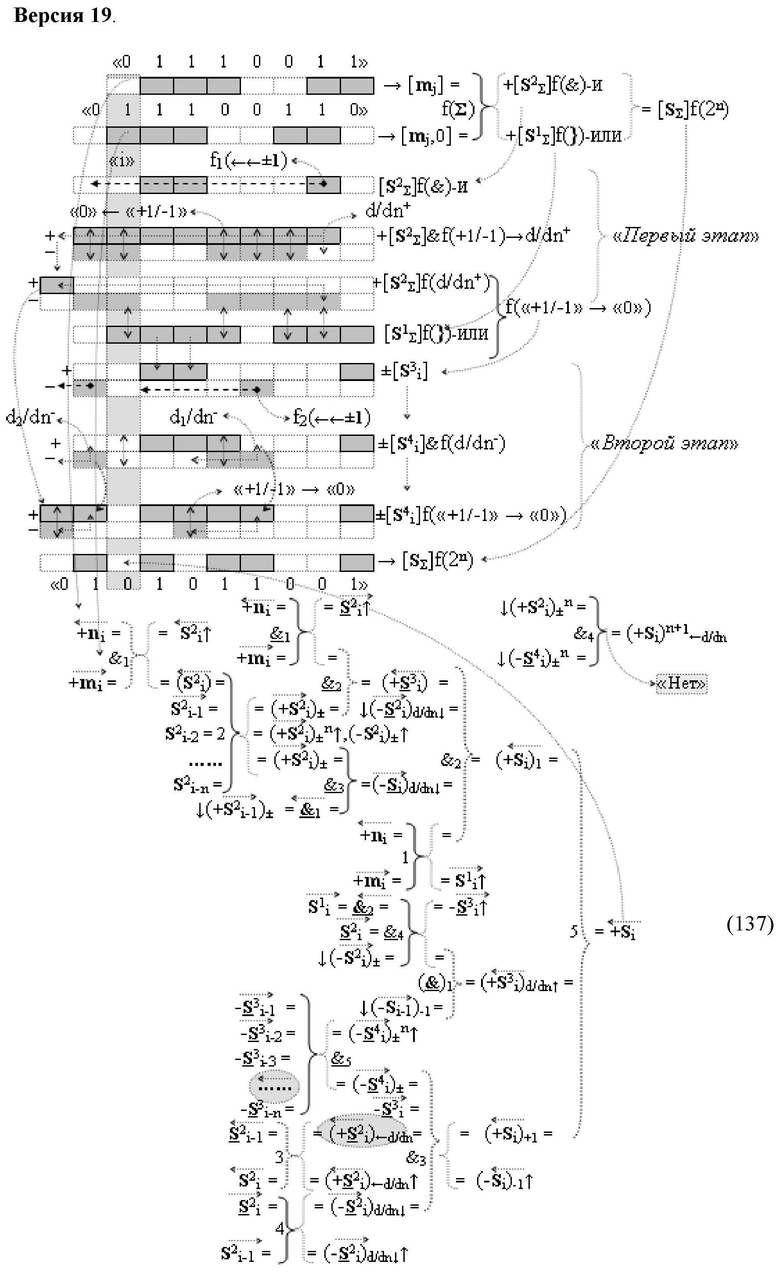

Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнения арифметических операций логического суммирования позиционных аргументов аналоговых сигналов [ni]f(2n) и [mi]f(2n) с применением арифметических аксиом троичной системы счисления f(+1,0,-1). Техническим результатом является повышение быстродействия суммирования. Способ заключается в следующем: формируют первую и вторую промежуточные суммы посредством логических элементов ИЛИ и И, а последующий процесс преобразования аргументов выполняют в два этапа, на «Первом этапе» выполняют сквозную активизацию не активных аргументов второй промежуточной суммы с последующим логическим дифференцированием только положительных результирующих аргументов и условно отрицательный аргумент этой процедуры включают в структуру условно отрицательных аргументов результата сквозной активизации не активных аргументов второй промежуточной суммы, посредством которых выполняют удаление соответствующих активных аргументов в структуре первой промежуточной суммы, формируют третью позиционно-знаковую промежуточную сумму, в которой активизируют очередные не активные аргументы после первого активного условно отрицательного аргумента в младшем разряде и формируют четвертую промежуточную сумму «Второго этапа» преобразования аргументов, в котором логически дифференцируют условно отрицательные аргументы с формированием только положительного аргумента этой процедуры и включают в результирующую структуру аргументов суммы, при этом на «Втором этапе» преобразования аргументов логически дифференцируют аргументы второй промежуточной суммы и положительным аргументом локального переноса этой процедуры исключают активизацию не активных аргументов третьей промежуточной суммы, а условно отрицательным аргументом локального переноса этой процедуры из результирующей структуры аргументов суммы исключают активный положительный аргумент третьей промежуточной суммы и формируют результирующую сумму аналоговых сигналов в позиционном формате.
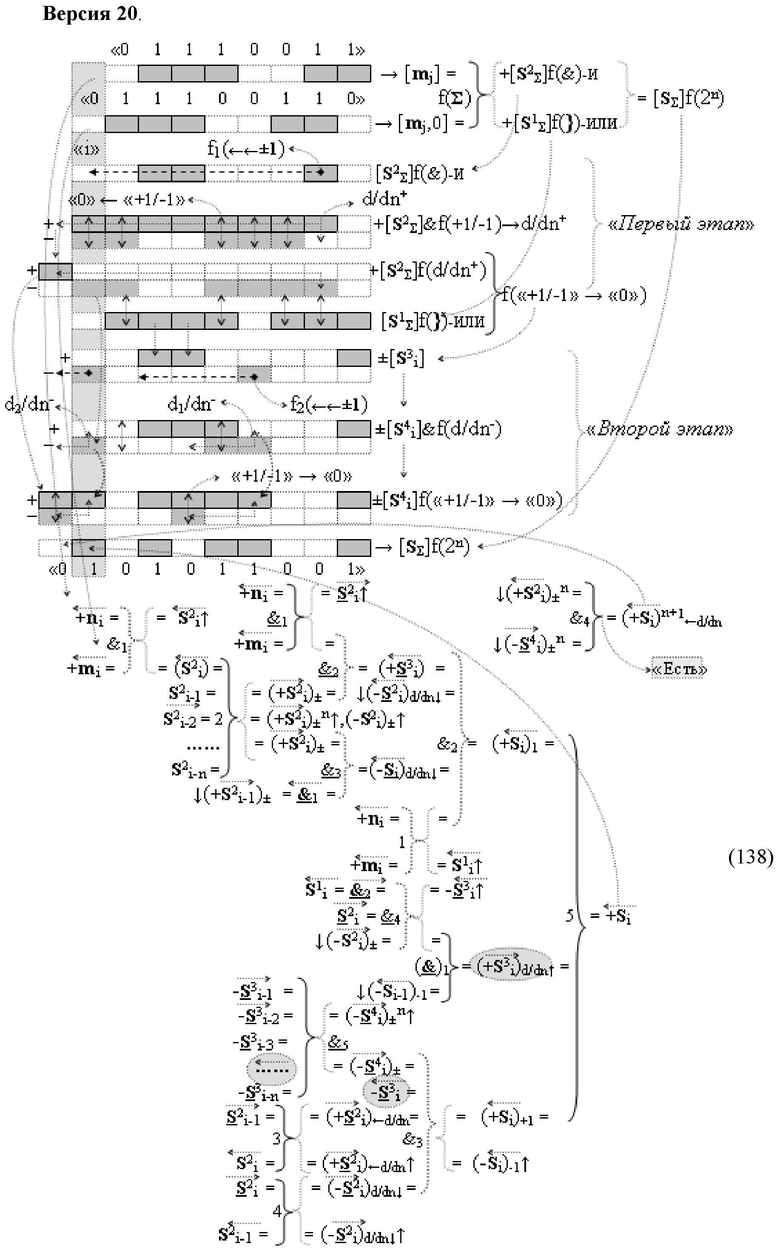
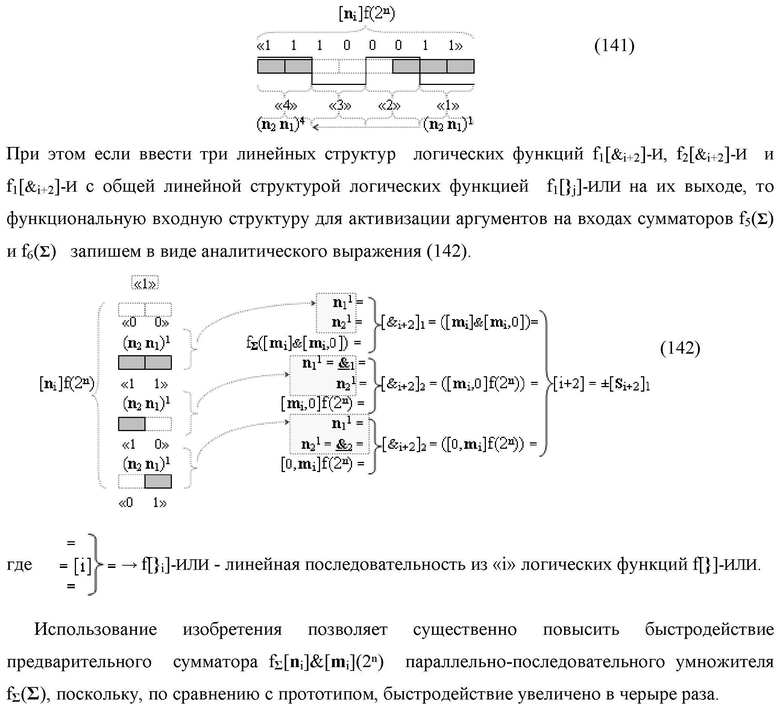
Способ реализации логического суммирования позиционных аргументов аналоговых сигналов слагаемых [ni]f(2n) и [mi]f(2n) частичных произведений в предварительном сумматоре fΣ[ni]&[mi](2n) параллельно-последовательного умножителя fΣ(Σ) с применением процедуры двойного логического дифференцирования d/dn+ и d/dn- промежуточных сумм и формированием результирующей суммы [Si]f(2n) в позиционном формате (Русская логика), в соответствии с которым выполняют в условно «i» разряде одновременный логический анализ позиционных аргументов аналогового сигнала nif(2n) и mif(2n) посредством логических функций с формированием первой и второй промежуточных сумм 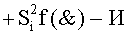 с измененным уровнем аналогового сигнала, отличающийся тем, что первую и вторую промежуточные суммы
с измененным уровнем аналогового сигнала, отличающийся тем, что первую и вторую промежуточные суммы  и
и 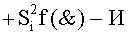 формируют посредством логических функций
формируют посредством логических функций 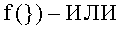 и
и 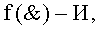 а последующий логико-динамический процесс преобразования аргументов выполняют в два этапа, на «Первом этапе» выполняют сквозную активизацию f1(←←±1) неактивных аргументов второй промежуточной суммы
а последующий логико-динамический процесс преобразования аргументов выполняют в два этапа, на «Первом этапе» выполняют сквозную активизацию f1(←←±1) неактивных аргументов второй промежуточной суммы 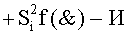 с последующим логическим дифференцированием d1/dn+ только положительных результирующих аргументов и условно отрицательный аргумент этой процедуры включают в структуру условно отрицательных аргументов результата сквозной активизации f1(←←±1) неактивных аргументов второй промежуточной суммы
с последующим логическим дифференцированием d1/dn+ только положительных результирующих аргументов и условно отрицательный аргумент этой процедуры включают в структуру условно отрицательных аргументов результата сквозной активизации f1(←←±1) неактивных аргументов второй промежуточной суммы 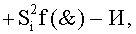 посредством которых выполняют удаление соответствующих активных аргументов в структуре первой промежуточной суммы
посредством которых выполняют удаление соответствующих активных аргументов в структуре первой промежуточной суммы 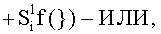 поскольку они формируют активные логические нули «+1/-1»→«0» и формируют третью позиционно-знаковую промежуточную сумму
поскольку они формируют активные логические нули «+1/-1»→«0» и формируют третью позиционно-знаковую промежуточную сумму 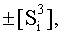 в которой активизируют очередные неактивные аргументы после первого активного условно отрицательного аргумента в младшем разряде, и формируют четвертую промежуточную сумму
в которой активизируют очередные неактивные аргументы после первого активного условно отрицательного аргумента в младшем разряде, и формируют четвертую промежуточную сумму 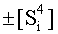 «Второго этапа» преобразования аргументов, в котором логически дифференцируют d1/dn- условно отрицательные аргументы с формированием только положительного аргумента этой процедуры и включают в результирующую структуру аргументов суммы
«Второго этапа» преобразования аргументов, в котором логически дифференцируют d1/dn- условно отрицательные аргументы с формированием только положительного аргумента этой процедуры и включают в результирующую структуру аргументов суммы 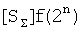 , при этом на «Втором этапе» преобразования аргументов логически дифференцируют d1/dn+ аргументы второй промежуточной суммы
, при этом на «Втором этапе» преобразования аргументов логически дифференцируют d1/dn+ аргументы второй промежуточной суммы 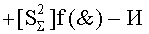 и положительным аргументом локального переноса +f2(←)d/dn этой процедуры исключают активизацию неактивных аргументов третьей промежуточной суммы
и положительным аргументом локального переноса +f2(←)d/dn этой процедуры исключают активизацию неактивных аргументов третьей промежуточной суммы 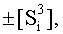 а условно отрицательным аргументом локального переноса -f2(↓)d/dn этой процедуры из результирующей структуры аргументов суммы [SΣ]f(2n) исключают активный положительный аргумент третьей промежуточной суммы
а условно отрицательным аргументом локального переноса -f2(↓)d/dn этой процедуры из результирующей структуры аргументов суммы [SΣ]f(2n) исключают активный положительный аргумент третьей промежуточной суммы 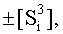 поскольку они формируют активные логические нули «+1/-1»→«0» и формируют результирующую сумму аналоговых сигналов [Sj]f(2n) в позиционном формате, в соответствии с логико-динамическим процессом вида
поскольку они формируют активные логические нули «+1/-1»→«0» и формируют результирующую сумму аналоговых сигналов [Sj]f(2n) в позиционном формате, в соответствии с логико-динамическим процессом вида 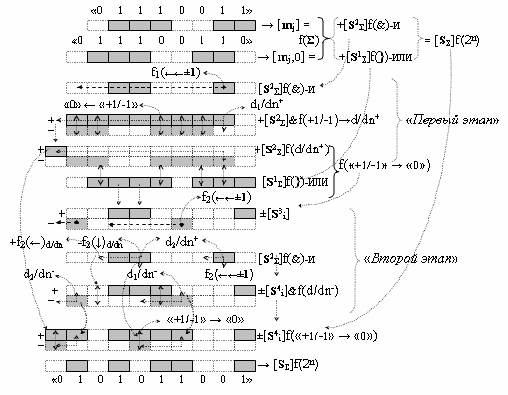
| Уэйкерли Дж | |||
| Проектирование цифровых устройств, т.1 | |||
| - М.: Постмаркет, 2002, с.508, рис.5.91 | |||
| СПОСОБ ПАРАЛЛЕЛЬНОГО ЛОГИЧЕСКОГО СУММИРОВАНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ АНАЛОГОВЫХ СИГНАЛОВ СЛАГАЕМЫХ ЭКВИВАЛЕНТНЫХ ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ | 2006 |
|
RU2378683C2 |
| СПОСОБ ПАРАЛЛЕЛЬНОГО ЛОГИЧЕСКОГО СУММИРОВАНИЯ АНАЛОГОВЫХ СИГНАЛОВ СЛАГАЕМЫХ, ЭКВИВАЛЕНТНЫХ ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ, И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2006 |
|
RU2375742C2 |
| JP 1304532 А, 08.12.1989 | |||
| JP 9016378 А, 17.01.1997. | |||
Авторы
Даты
2012-03-27—Публикация
2010-07-22—Подача