Текст описания приведен в факсимильном виде. 
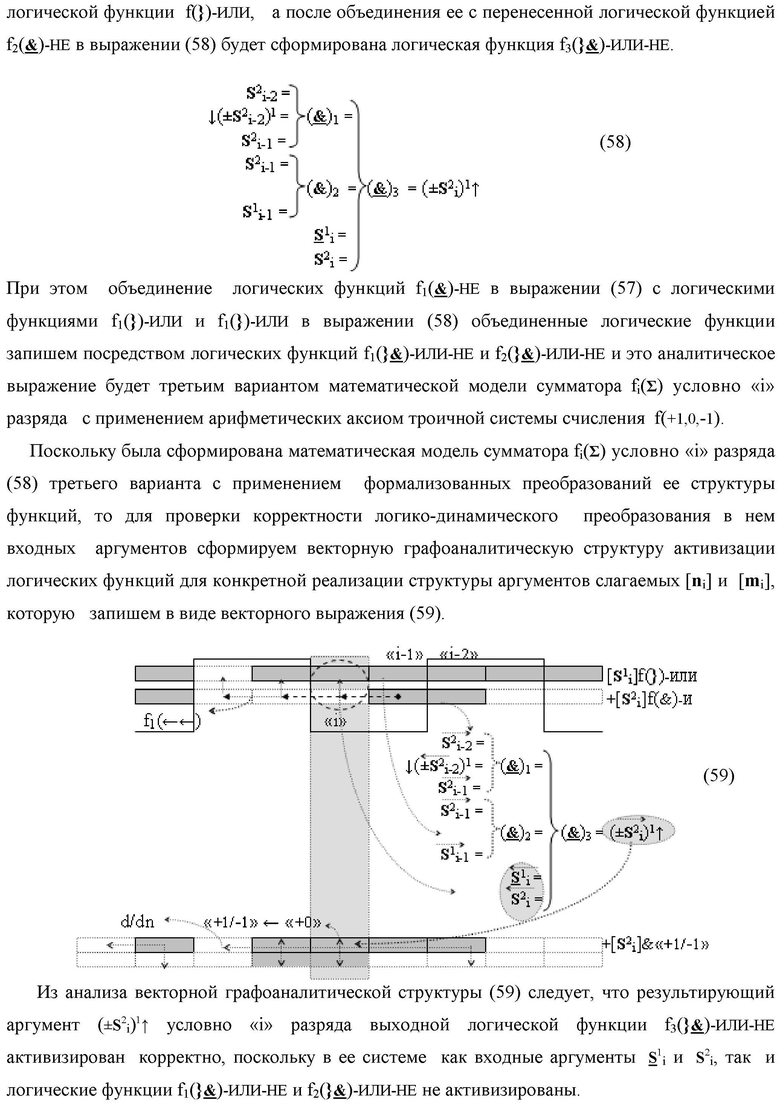
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств для выполнения арифметических процедур суммирования позиционных аргументов [ni]f(2n) и [mi]f(2n). Техническим результатом является повышение быстродействия суммирования. В одном из вариантов функциональная структура реализована с использованием логических элементов И, ИЛИ. 5 н.п. ф-лы.
1. Функциональная структура логико-динамического процесса последовательной сквозной активизации неактивных аргументов «0» второй промежуточной суммы
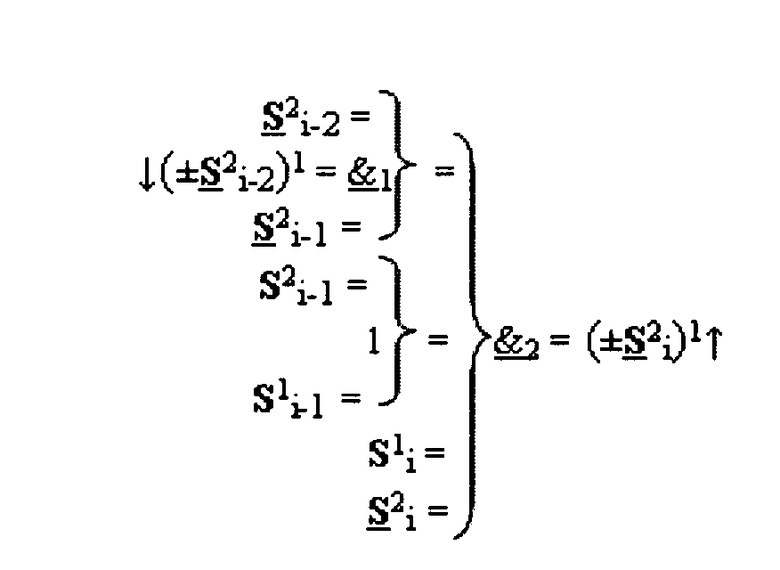
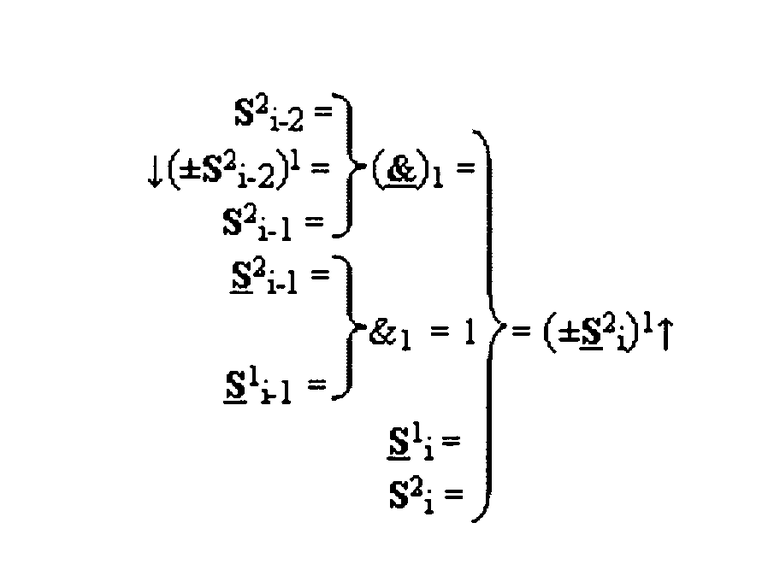
+[S2 i]f(&)-И в сумматоре f(Σ) при преобразовании позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n), для выполнения анализа аргументов первой промежуточной суммы [S1 i]f(2n) сформированных из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(})-ИЛИ, и второй промежуточной суммы, сформированной из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(&)-И, условно «i» разряд которой для выполнения анализа входных аргументов и формирования результирующего аргумента (±S2 i)1 активизации включает логические функции f1(})-ИЛИ, f2(})-ИЛИ и логическую функцию f1(&)-И, отличающаяся тем, что функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
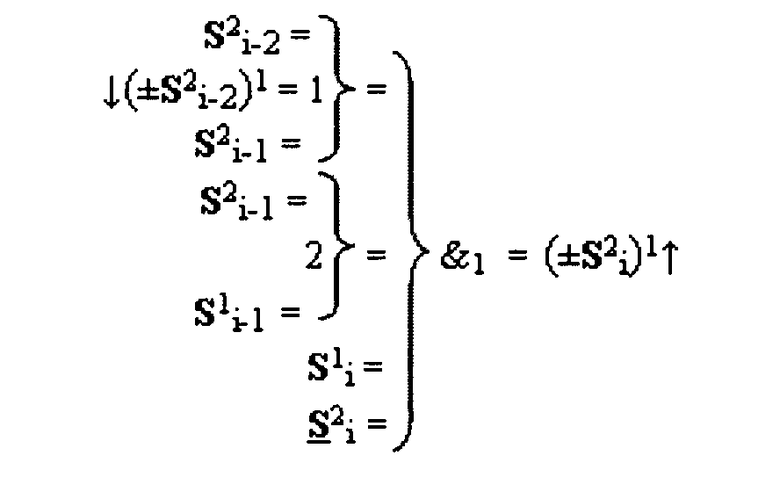
где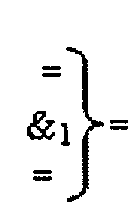 
- логическая функция f1(&)-И; 
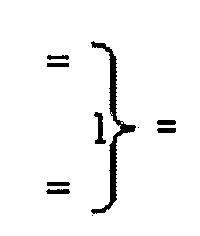- логическая функция f1(})-ИЛИ.
2. Функциональная структура логико-динамического процесса последовательной сквозной активизации неактивных аргументов «0» второй промежуточной суммы
+[S2 i]f(&)-И в сумматоре f(Σ) при преобразовании позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n), для выполнения анализа аргументов первой промежуточной суммы [S1 i]f(2n) сформированных из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(})-ИЛИ, и второй промежуточной суммы, сформированной из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(&)-И, условно «i» разряд которой для выполнения анализа входных аргументов и формирования результирующего аргумента (±S2 i)1 активизации включает логическую функцию f1(})-ИЛИ, отличающаяся тем, что введены дополнительные логические функции fi(&)-И-HE и f2(&)-И-НЕ, а функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
где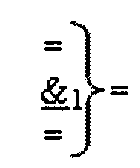 
- логическая функция f1(&)-И-HE.
3. Функциональная структура логико-динамического процесса последовательной сквозной активизации не активных аргументов «0» второй промежуточной суммы
+[S2 i]f(&)-И в сумматоре f(Σ) при преобразовании позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n), для выполнения анализа аргументов первой промежуточной суммы [S1 i]f(2n) сформированных из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(})-ИЛИ, и второй промежуточной суммы, сформированной из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(&)-И, условно «i» разряд которой предназначен для анализа входных аргументов и формирования результирующего аргумента (±S2 i)1 активизации, отличающаяся тем, что введены дополнительные логические функции f1(}&)-ИЛИ-HE, f2(}&)-ИЛИ-HE и f3(}&)-ИЛИ-НЕ, а функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
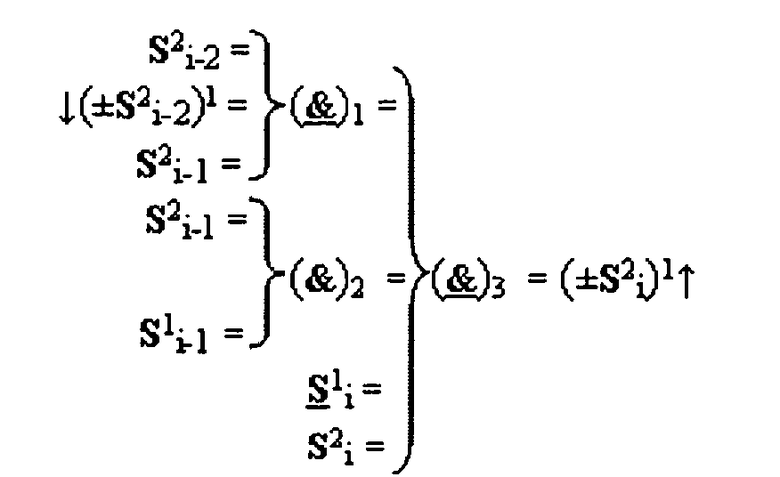
где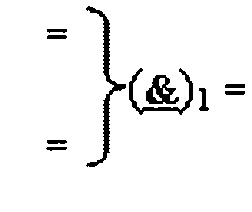 
- логическая функция f1(}&)-ИЛИ-HE.
4. Функциональная структура логико-динамического процесса последовательной сквозной активизации неактивных аргументов «0» второй промежуточной суммы
+[S2i]f(&)-И в сумматоре f(Σ) при преобразовании позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n), для выполнения анализа аргументов первой промежуточной суммы [S1 i]f(2n) сформированных из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(})-ИЛИ, и второй промежуточной суммы, сформированной из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(&)-И, условно «i» разряд которой включает логическую функцию f1(&)-И для выполнения анализа входных аргументов, функциональная выходная связь которой является функциональной входной связью выходной логической функции f1(})-ИЛИ, в которой функциональная выходная связь является функциональной выходной связью структуры для формирования результирующего аргумента (±S2 i)1 активизации, отличающаяся тем, что введена дополнительная логическая функция f1(}&)-ИЛИ-НЕ, а функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
5. Функциональная структура логико-динамического процесса последовательной сквозной активизации неактивных аргументов «0» второй промежуточной суммы
+[S2 i]f(&)-И в сумматоре f(Σ) при преобразовании позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n), для выполнения анализа аргументов первой промежуточной суммы [S1 i]f(2n) сформированных из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(})-ИЛИ, и второй промежуточной суммы, сформированной из входных позиционных аргументов слагаемых [ni]f(2n) и [mi]f(2n) посредством логической функции fi(&)-И, условно «i» разряд которой включает логическую функцию fi(&)-И для выполнения анализа входных аргументов, функциональная выходная связь которой является функциональной входной связью выходной логической функции f1(})-ИЛИ, в которой функциональная выходная связь является функциональной выходной связью структуры для формирования результирующего аргумента (±S2 i)1 активизации, отличающаяся тем, что введена дополнительная логическая функция f1(}&)-ИЛИ-НЕ, а функциональные связи в функциональной структуре выполнены в соответствии с математической моделью вида
| УЭЙКЕРЛИ ДЖ | |||
| Проектирование цифровых устройств | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Устройство для параллельного сложения чисел, представленных в двоичной знакоразрядной системе счисления | 1989 |
|
SU1727120A1 |
| Устройство для параллельного алгебраического сложения в знакоразрядной системе счисления | 1981 |
|
SU1003074A1 |
| JP 2002082798 A, 22.03.2002 | |||
| JP 63197227 A, 16.08.1988 | |||
| US 5907499 A, 25.05.1999. | |||
