Изобретение относится к способам определения пространственной ориентации при угловом движении подвижных объектов, преимущественно летательных аппаратов (ЛА), относительно какой-либо базовой системы координат, путем аналитического ее вычисления на основе измерений каких-либо отдельных параметров ориентации (углов, угловых скоростей и т.д.).
Задачам управления движением ЛА посвящено большое число публикаций в нашей стране и за рубежом. Однако сложность стоящих здесь проблем, отсутствие общих аналитических решений и трудности численного решения дифференциальных краевых задач, к которым сводятся задачи оптимального управления пространственным движением ЛА, продолжают оставлять эту проблематику актуальной.
Многие авторы рассматривают задачу управления угловым движением ЛА как с использованием классических моделей в угловых переменных, так и с помощью кватернионных моделей. Необходимо отметить работы А.В. Молоденкова, Я.Г. Сапункова [1-3], Ю.Н. Челнокова [4-9], посвященные данной тематике.
Изменение ориентации твердого тела в пространстве может быть выполнено различными способами: посредством трех последовательных разворотов вокруг трех связанных осей [10], одним плоским разворотом вокруг эйлеровой оси [10-13], несколькими плоскими разворотами [14], либо одним пространственным разворотом. Вопросы оптимального управления эйлеровым или экстенсивным [12] разворотом нашли в литературе наиболее полное отражение. Как отмечается в [14], этот способ особенно эффективен, когда эллипсоид инерции близок к сфере или управление осуществляется малыми по величине управляющими моментами. В работе В.И. Гуляева, В.Л. Кошкина, И.В. Савиловой [15] решение задачи оптимального управления ориентацией твердого тела строится в более общем классе пространственных поворотов без дополнительных ограничений на характер результирующего движения.
При использовании для описания положения тела какой-либо системы углов, в частности углов Эйлера, возникают трудности, обусловленные наличием в уравнениях движения особенностей, когда угол нутации становится кратным 90°. Переход от углов Эйлера к кватерниону поворота позволяет устранить особенность в кинематических уравнениях, однако система оказывается управляемой лишь на интегральном многообразии, описываемом первым интегралом кинематических уравнений в параметрических переменных, что затрудняет решение задачи. В работе [15] предлагается подход, при котором задача оптимизации управления формулируется в терминах физических переменных (углах Эйлера), а интегрирование системы уравнений движения и уравнений в вариациях осуществляется в параметрах Родрига-Гамильтона [6] с последующим использованием при построении оптимального управления регуляризующих матриц перехода.
Большое количество работ посвящено изучению задачи оптимального по быстродействию управления, угловым движением летательного аппарата - твердого тела, однако эта задача в общей постановке до настоящего времени далека от завершения. Среди работ, посвященных решению этой задачи в различных постановках с использованием аппарата кватернионов, отметим работы В.Н. Бранеца [4-6,16,17], И.П. Шмыглевского [4-16, 17], М.Б. Чертока, Ю.В. Казначеева [16], Д.В. Лебедева [18], А.Н. Сиротина [19-21], А.В. Молоденкова, Я.Г. Сапункова [2].
Обширный обзор литературы по задаче оптимальной, в смысле быстродействия переориентации летательного аппарата, содержится в монографии [22]. В этой монографии отмечается, что при исследовании динамических задач оптимального по быстродействию управления движением объектов, когда в качестве управляющего воздействия выступает вектор моментов внешних сил, основная аналитическая трудность заключается в рассмотрении оптимального по быстродействию управления ориентацией твердого тела. Обычно решение данной задачи разбивается на две подзадачи: торможение (гашение) вращений и переориентация твердого тела (начальное и конечное положения тела заданы и являются состояниями покоя). В работе [22] отмечается, что если торможение вращений достаточно полно исследовано, то задача оптимального по быстродействию управления переориентацией твердого тела в полной постановке является задачей нерешенной, тем более далека от завершения общая задача синтеза оптимальных управлений ориентацией твердого тела (с одновременным гашением угловой скорости).
Для определения углового положения подвижного объекта относительно некоторой базовой системы координат служат системы ориентации (БСО) на основе датчиков, устанавливаемых непосредственно на корпусе подвижного объекта, при этом реализуется бесплатформенная инерциальная навигационная система построения (БИНС). В современных БИНС путем интегрирования и преобразования рассчитанных значений скорости получают текущие значения координат объекта в базовой системе координат, а затем по формулам находят значения проекций скорости в базовой системе координат. Известно, что большим недостатком БИНС является неустойчивость погрешности счисления координат к внутренним возмущениям, например, инструментальным погрешностям, вызванным тем, что координаты объекта находят путем интегрирования и преобразования скорости. Вследствие этого погрешности счисления координат и, следовательно, проекций скорости имеют расходящийся характер. При существующей схеме построения этот недостаток БИНС ухудшает точность работы БСО, а первопричиной этому является со стороны БСО необходимость определения скорости для решения задачи ориентации, со стороны БИНС расходящийся характер погрешности определения координат и скорости.
Известен способ определения параметров ориентации и навигации подвижных объектов по патенту RU 2059205 (МПК: G01С 21/00, опубл. 27.04.1996), включающий в себя измерение абсолютных угловых скоростей и ускорений объекта, определение угловых скоростей и ускорений базовой системы координат, после чего определяют относительные угловые ускорения объекта путем решения уравнения угловых ускорений, связывающего ускорения объекта и базовой системы координат, затем определяют относительные угловые скорости объекта путем решения уравнения угловых скоростей проекции угловой скорости Земли на оси базовой системы координат, определяют координаты объекта либо путем решения алгебраических уравнений, связывающих координаты и проекции угловой скорости Земли, либо путем интегрирования относительных линейных скоростей. Этим из структурной схемы БИНС устраняется второй интегратор, с помощью которого в БИНСе вычисляются координаты объекта и который является причиной расходящегося характера погрешности вычисления в БИНСе координат объекта и проекций угловой скорости собственного вращения Земли.
Недостатком данного известного способа является то, что невозможно обеспечить необходимую точность определения угловых параметров быстровращающихся подвижных объектов.
Известен способ определения углового положения подвижного объекта по патенту RU 2343418 (МПК: G01С 21/10, опубл. 10.01.2009), принятый за наиболее близкий аналог. Для определения места точки на поверхности Земли и околоземном пространстве используют системы координат, жестко связанные с Землей - геоцентрические системы. Таких систем много. В данном способе используют одну из разновидностей, так называемую горизонтальную систему координат OXYZ, в которой горизонтальная ось ОХ направлена в сторону северного географического полюса и касается географического меридиана, горизонтальная ось OY направлена на восток, а вертикальная ось OZ совпадает с линией отвеса или геоцентрической вертикали. Горизонтальную систему координат OXYZ принимают за требуемую.
Для определения положения подвижного объекта - носителя измерительного устройства в пространстве используют систему координат, жестко связанную с объектом, так называемую связанную систему координат OX1Y1Z1. Определяют начало координат этой системы в центре масс объекта, ось ОХ1 направляют вперед по продольной оси, ось OY1 - вправо, а ось OZ1 - вниз к центру Земли. Положение связанной системы координат объекта OX1Y1Z1 относительно горизонтальной системы координат OXYZ, в которой определен вектор силы тяжести G и которая является требуемой, определяется тремя направляющими косинусами вектора силы тяжести G в связанной системе координат объекта. Решение этой задачи датчиком устройства для определения углового положения подвижного объекта производят способом одновременного измерения проекций вектора силы тяжести G на плоскости связанной системы координат произвольно расположенного в пространстве датчика устройства. При совмещении связанной системы координат объекта с горизонтальной системой координат, в которой определен вектор силы тяжести G, показания датчика принимают за начало отсчета, затем на маршруте движения по результатам измерений вычисляют навигационные параметры (истинный курс, крен и тангаж), а также значения ускорения вектора силы тяжести. Известный способ реализуется путем одновременного измерения проекций вектора G на координатные плоскости связанной системы координат устройства, а не составляющих вектора силы тяжести на оси этой системы. Измерения производятся с произвольно расположенного в пространстве устройства.
Недостатком ближайшего аналога является ограниченность области применения из-за принципа подхода при создании базовой и требуемой систем координат. Кроме того, применение гравиметрических измерений накладывает определенные требования на условия их применения, что может привести к выдаче данных, которые отличаются от реальных, в частности, навигационные параметры (истинный курс, крен и тангаж).
Техническим результатом заявляемого изобретения является расширение области применения, повышение достоверности и точности определения углового положения подвижного объекта.
Указанный технический результат достигается за счет того, что в способе определения углового положения подвижного объекта относительно центра масс, включающем определение связанной с подвижным объектом текущей угловой ориентации системы координат OX1Y1Z1, с началом координат в центре масс объекта, относительно геоцентрической базовой системы координат OXYZ, задание требуемой угловой ориентации системы координат, определение текущих значений углов ориентации связанной системы координат относительно базовой, перевод связанной системы координат из текущей угловой ориентации в требуемую с последующим вычислением параметров, по которым судят об угловом положении подвижного объекта, новым является то, что задают требуемую угловую ориентацию системы координат OX2Y2Z2, связанную с подвижным объектом, с началом координат в центре масс объекта, а параметрами, по которым судят об угловом положении подвижного объекта, являются углы относительной ориентации ςx, ςy, ςz между соответствующими осями связанной системы текущей угловой ориентации и требуемой в геоцентрической базовой системе координат, для чего определение текущих значений углов ориентации собственной системы координат подвижного объекта относительно геоцентрической базовой системы координат производят с помощью бесплатформенной инерциальной навигационной системы (БИНС), в геоцентрической базовой системе направление оси OZ принимают совпадающим с направлением вектора вращения Земли, а ось ОХ направлена в точку пересечения гринвичского меридиана с экватором, причем при переводе связанной системы координат из текущей угловой ориентации в требуемую принимают, что требуемая угловая ориентация связанной системы координат относительно геоцентрической базовой системы координат является неподвижной, саму требуемую связанную систему координат OX2Y2Z2 считают инерциальной и дальнейший процесс вычисления параметров осуществляют относительно этой неподвижной системы координат, углы относительной ориентации ςx, ςy, ςz определяют по следующим зависимостям:
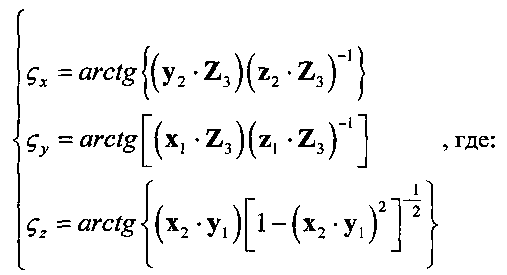
где Z3=(х2×y1)|х2×y1|-1 - промежуточная ось между OZ1 и OZ2; x1={x1x; x1y; x1z}, y1={y1x; y1y; y1z}, z1={z1x; z1y; z1z} - оси текущей связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат; x2={x2x; x2y; x2z}, y2={y2x; y2y; y2z}, z2={z2x; z2y; z2z} - оси требуемой связанной системы координат подвижного объекта в проекциях на оси геоцентрической инерциальной системы координат;
OX2Y2Z2 - оси требуемой связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат.
Задание требуемой угловой ориентации системы координат OX2Y2Z2, связанной с подвижным объектом, с началом координат в центре масс объекта, позволяет снять ограничения на величину требуемых углов ориентации, что дает возможность алгоритму переориентации и стабилизации устойчиво выполнять целевую задачу.
Определение углов относительной ориентации ςх, ςу, ςz между соответствующими осями связанной системы текущей угловой ориентации и требуемой в геоцентрической базовой системе координат, по которым судят об угловом положении подвижного объекта, позволяет избежать влияния перекрестных связей на алгоритм переориентации и стабилизации.
Определение текущих значений углов ориентации собственной системы координат подвижного объекта относительно геоцентрической базовой системы координат производят с помощью БИНС, позволяет упростить схемотехническое решение и облегчить реализации конструкции навигационной системы.
Принятие в геоцентрической базовой системе направление оси OZ совпадающим с направлением вектора вращения Земли, а ось ОХ направлена в точку пересечения гринвичского меридиана с экватором, позволяет достичь наибольшей методической точности результатов работы алгоритмов БИНС.
Принятие при переводе связанной системы координат из текущей угловой ориентации в требуемую, что требуемая угловая ориентация связанной системы координат относительно геоцентрической базовой системы координат является неподвижной, сама требуемая связанная система координат OX2Y2Z2 - инерциальная, и осуществление дальнейшего процесса вычисления параметров относительно этой неподвижной системы координат позволяет вычислять параметры в контуре решения основного уравнения навигации БИНС, что упрощает применение алгоритма переориентации и стабилизации.
Определение углов относительной ориентации ςх, ςу, ςz по вышеуказанным зависимостям позволяет упростить вычисления и реализовать способ более простыми техническими средствами.
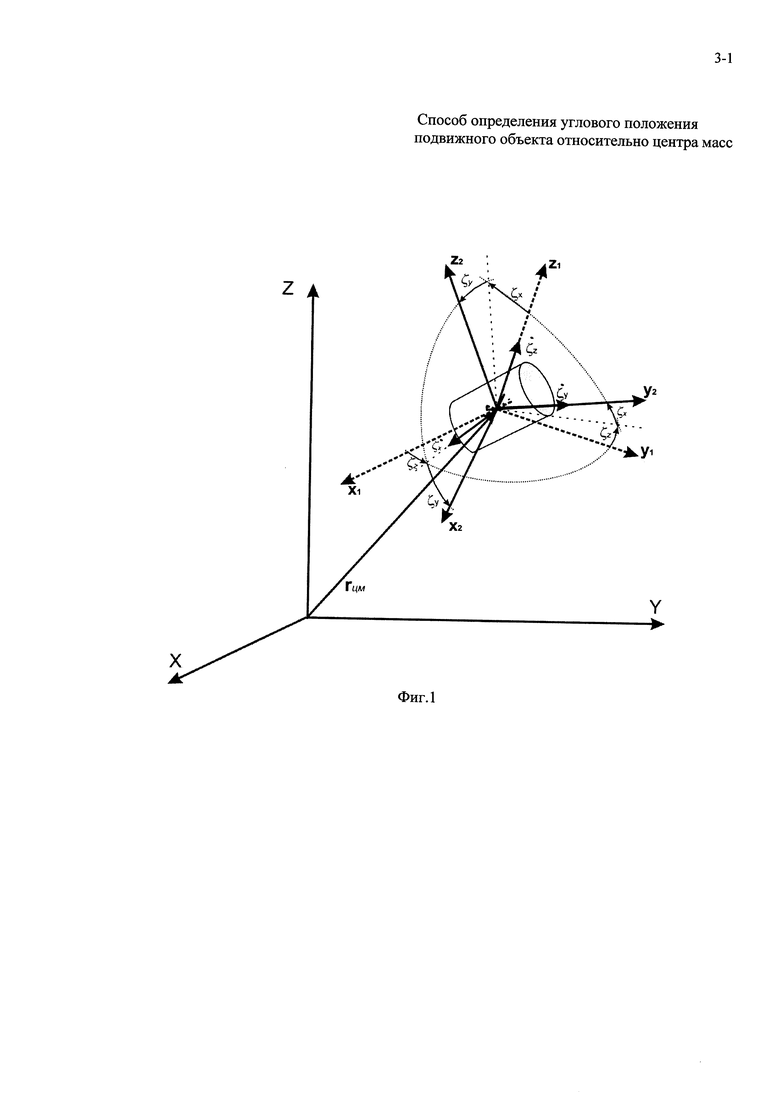
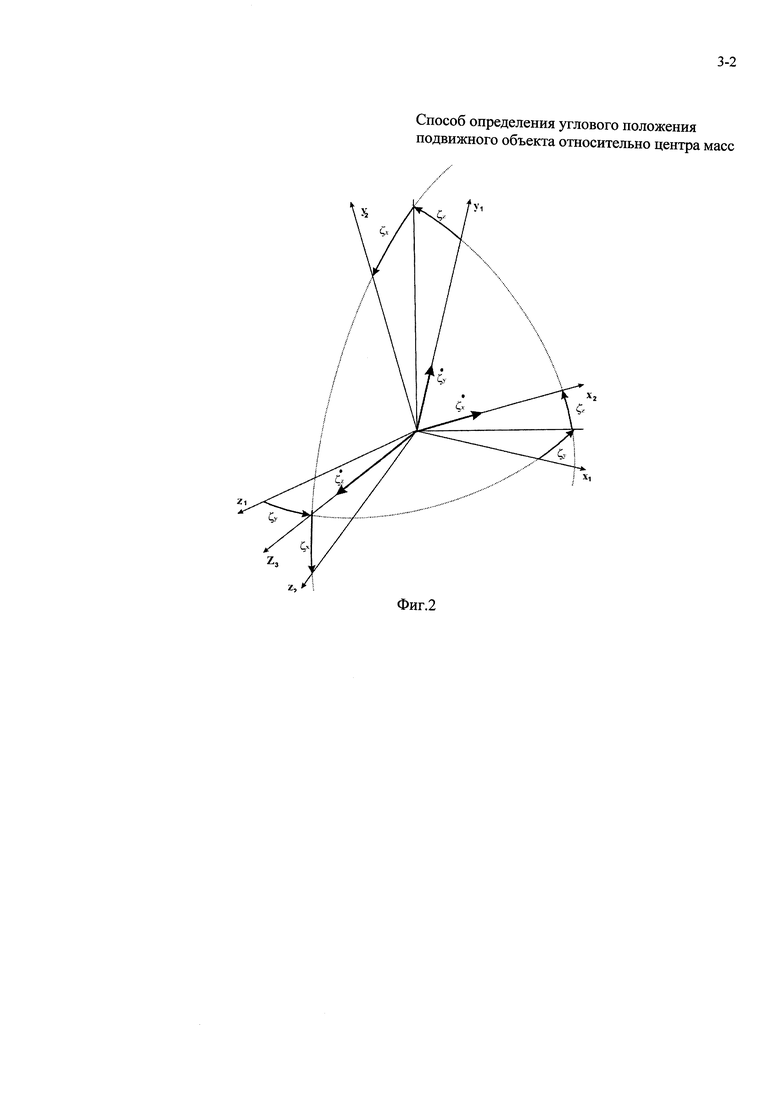
На фиг. 1 представлено взаимное положение геоцентрической базовой системы координат OXYZ, текущей связанной OX1Y1Z1 и требуемой связанной OX2Y2Z2 систем координат. На фиг. 2 - пояснение к определению углов относительной ориентации ςх, ςу, ςz, между соответствующими осями связанной системы текущей угловой ориентации и требуемой в геоцентрической базовой системе координат, где:
OX1Y1Z1 - оси текущей связанной системы координат относительно геоцентрической базовой системы координат OXYZ;
OX2Y2Z2 - оси требуемой связанной системы координат относительно геоцентрической базовой системы координат;
rцм - радиус-вектор центра масс аппарата в геоцентрической базовой системе координат;
Z3 - промежуточная ось между OZ1 и OZ2.
Примером конкретного выполнения заявляемого изобретения может служить способ управления угловым движением летательного аппарата (ЛА) относительно центра масс при одновременной работе двигательных установок по всем каналам управления ориентацией без наложения ограничений на величину текущих и требуемых углов ориентации связанной системы координат аппарата относительно геоцентрической базовой системы координат. Способ применим для ЛА, управляющее усилие которых создается реактивными, многоразовыми двигателями.
Движение летательного аппарата вокруг центра масс состоит из переориентации в заданное угловое положение в инерциальной системе координат и стабилизации продольной оси объекта около этого положения. При синтезе алгоритма переориентации предполагалось, что летательный аппарат - это твердое тело с неизменными положением центра масс и моментами инерции, не содержащее каких-либо движущихся масс, в частности гиросиловых стабилизаторов. Для синтеза контура переориентации и стабилизации использовался принцип максимума Понтрягина. Измерение текущих значений углов ориентации связанной системы координат аппарата относительно геоцентрической базовой системы координат производится с помощью БИНС. Требуемые углы ориентации выдаются системой управления ЛА как условие решения поставленной целевой задачи.
В каждый момент времени текущее положение связанной системы координат ЛА относительно геоцентрической базовой системы координат "замораживается", сама связанная система координат начинает считаться инерциальной и дальнейший процесс вращательного движения осуществляется относительно этой "замороженной" системы координат. При таком способе требуемое значение угла 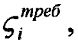 которое подается в систему управления для переориентации, равно нулю. А необходимое для алгоритма переориентации и стабилизации значение текущего угла ςi будет определяться как угол между соответствующими осями текущей и требуемой связанной системы координат в геоцентрической базовой системе координат (фиг. 1). Получается, что на каждом шаге определения текущих значений углов ориентации относительно геоцентрической базовой системы координат как бы "докручивается" текущая ориентация связанной системы координат ЛА до требуемого положения.
которое подается в систему управления для переориентации, равно нулю. А необходимое для алгоритма переориентации и стабилизации значение текущего угла ςi будет определяться как угол между соответствующими осями текущей и требуемой связанной системы координат в геоцентрической базовой системе координат (фиг. 1). Получается, что на каждом шаге определения текущих значений углов ориентации относительно геоцентрической базовой системы координат как бы "докручивается" текущая ориентация связанной системы координат ЛА до требуемого положения.
Углы относительной ориентации осей текущей связанной системы координат ЛА и требуемой определяются из следующих зависимостей
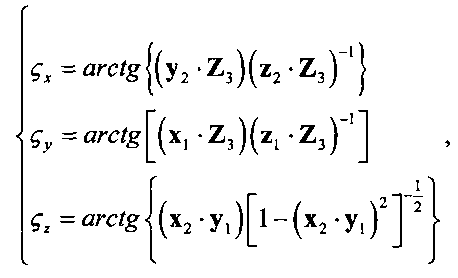
где Z3=(х2×y1)|х2×y1|-1 - промежуточная ось между OZ1 и OZ2; x1={x1x; x1y; x1z}, y1={y1x; y1y; y1z}, z1={z1x; z1y; z1z} - оси текущей связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат; x2={x2x; x2y; x2z}, y2={y2x; y2y; y2z}, z2={z2x; z2y; z2z} - оси требуемой связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат.; ςх, ςу, ςz - углы относительной ориентации текущей связанной системы координат OX1Y1Z1 ЛА и требуемой связанной системы координат OX2Y2Z2 аппарата.
Оси текущей связанной системы координат OX1Y1Z1 в проекциях на оси геоцентрической инерциальной системы координат OXYZ определяются столбцами матрицы пересчета А1о/и=[х1, у1, z1], которая вычисляется в контуре решения основного уравнения навигации БИНС. Оси требуемой связанной системы координат OX2Y2Z2 в проекциях на оси геоцентрической инерциальной системы координат OXYZ определяются столбцами матрицы пересчета A2о/и=[х2, у2, z2], которая также вычисляется в контуре решения основного уравнения навигации БИНС.
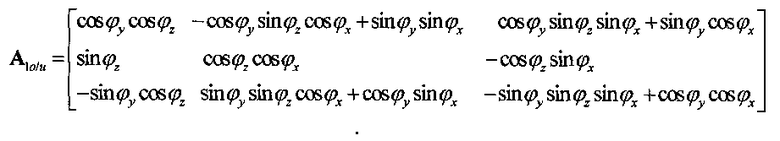
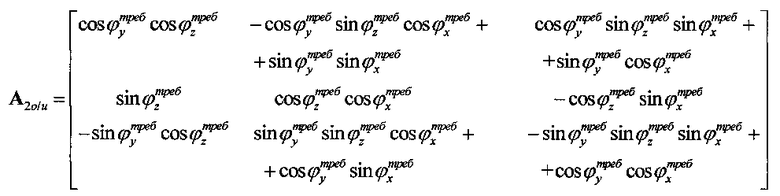
Здесь φx, φy, φz - текущие углы ориентации связанной системы координат ЛА относительно геоцентрической базовой системы координат; 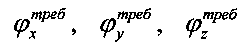 - требуемые углы ориентации связанной системы координат ЛА относительно геоцентрической базовой системы координат.
- требуемые углы ориентации связанной системы координат ЛА относительно геоцентрической базовой системы координат.
Формулы для вычисления производных по времени углов ориентации (фиг. 2) имеют вид
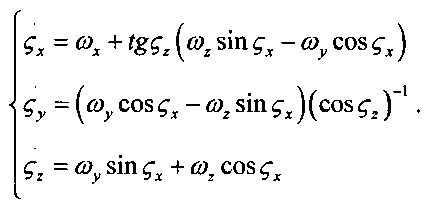
Здесь ωx, ωy, ωz - проекции вектора абсолютной угловой скорости ЛА на оси связанной системы координат ЛА, соответственно.
Т.о. заявляемый способ позволяет в течение длительного времени отслеживает необходимое направление продольной оси ЛА в инерциальном пространстве для различных законов изменения значений требуемых углов ориентации.
Сравнение полученных длительностей процесса с оптимальными значениями, полученными, исходя из предположения о независимости друг от друга каналов управления ориентацией ЛА, показало, что полученные значения времен процесса близки к оптимальным значениям, а сам алгоритм можно считать близким к оптимальному алгоритму.
Источники информации
1. Петухов, В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами / В.Г. Петухов // Космические исследования. 2004. - Т. 42. - Вып. 3. - С. 260-279.
2. Петухов, В.Г. Оптимизация межпланетных траекторий космических аппаратов с идеально-регулируемым двигателем методом продолжения / В.Г. Петухов // Космические исследования; - 2008 - Т. 46. Вып. 3. - С. 224-237.
3. Пимкина, Т.В. Краевая задача оптимального управления орбитальным движением космического аппарата пониженной размерности / Т.В. Пимкина, Ю.Н. Челноков // Математика. Механика: Сб. науч. тр. - 2003. - Вып. 5. - С. 168-171.
4. Бранец, В.Н. Кинематические задачи ориентации во вращающейся системе координат / В.Н. Бранец, И.П. Шмыглевский // Изв. АН СССР. Механика твердого тела. - 1972. - №6. - С. 36-43.
5. Бранец, В.Н. Применение кватернионов в задачах ориентации твердого тела / В.Н. Бранец, И.П. Шмыглевский. - М.: Наука, 1973. - 320 с.
6. Бранец, В.Н. Введение в теорию бесплатформенных инерциальных навигационных систем / В.Н. Бранец, И.П. Шмыглевский. - М.: Наука, 1992. - 278 с.
7. Рыжов, С.Ю. К проблеме решения задач оптимизации многовитковых траекторий межорбитальных перелетов КА / С.Ю. Рыжов, И.С. Григорьев // Космические исследования. - 2006. - Т. 44. Вып. 3. - С. 272-280
8. Сапунков, Я.Г. Оптимальное управление движением космического аппарата в нецентральном поле гравитации Земли / Я.Г. Сапунков // Математика. Механика: Сб. науч. тр. - 2005. Вып. 7. - С. 192-195.
9. Черноусько, Ф.Л. Управление колебаниями / Ф.Л. Черноусько, Л.Д. Акуленко, Б.Н. Соколов. - М.: Наука, 1980. - 380 с.
10. Пак, Ч.В. Использование ограниченных по величине импульсов для коррекции траектории / 4. В. Пак // Космические исследования. - 1998. - Т. 36. Вып. 2 - С. 177-182.
11. Алексеев, К.Б. Экстенсивное управление ориентацией космических летательных аппаратов / К.Б. Алексеев. - М.: Машиностроение, 1977. - 121 с.
12. Салмин, В.В. Приближенный расчет маневров формирования орбиты спутника Земли с двигателем малой тяги / В.В. Салмин, В.О. Соколов // Космические исследования. - 1991. - Т. 29: Вып. 6. - С. 872-888.
13. Kiforenko, В.М. Quasioptimal interorbit transfers of a low-thrust spacecraft in strong central newtonian gravity field / В.M. Kiforenko, I.Yu. Vasil'ev // Acta Astronáutica. 2009. - Vol. 65. - №1-2. - P. 82-94.
14. Mabsout, В.E. The optimization of the orbital hohmann transfer / В.E. Mabsout, O. M. Kamel, A.S. Soliman // Acta Astronáutica. - 2009. - Vol. 65. №7-8. - P. 1094-1097.
15. Ивашкин, В.В. Оптимизация двухимпульсного маневра встречи двух аппаратов на круговой орбите при наличии ограничений / В.В. Ивашкин, Г.Г. Райкунов // Космические исследования. - 1991. - Т. 29. Вып. 3. - С. 352-366.
16. Бранец, В.Н. Применение кватернионов в управлении угловым положением твердого тела / В.Н. Бранец, И.П. Шмыглевский // Изв. АН СССР. Механика твердого тела. - 1972. - №4. - С. 24-31.
17. Брумберг, В.А. Аналитические алгоритмы небесной механики / В.А. Брумберг. - М.: Наука, 1980. - 208 с.
18. Молоденков, А.В. Аналитическое решение импульсной задачи оптимального разворота космического аппарата / А.В. Молоденков, Я.Г. Сапунков // Математика. Механика: Сб. науч. тр. - 2000. Вып. 2. - С. 173-174.
19. Челноков, Ю.Н. Управление ориентацией космического аппарата, использующее кватернионы / Ю.Н. Челноков // Космические исследования. 1994. - Т. 32. - Вып. 3. - С. 21-32.
20. Челноков, Ю.Н. Кватернионное построение оптимальных управлений и траекторий движения космического аппарата, в ньютоновском гравитационном поле / Ю.Н. Челноков, В.А. Юрко // Изв. РАН. Механика твердого тела. - 1996. - №6. - С. 3-13.
21. Челноков, Ю.Н. Построение оптимальных управлений и траекторий космического аппарата на основе регулярных кватернионных уравнений задачи двух тел / Ю.Н. Челноков, Я.Г. Сапунков // Космические исследования. - 1996. - Т. 34. Вып. 2. - С. 150-158.
22. Панков, А.А. Исследование кватернионных законов кинематического управления ориентацией твердого тела по угловой скорости / А.А. Панков,. Ю.Н. Челноков // Изв. РАН. Механика твердого тела. - 1995. - №6. - С. 3-13.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| Способ определения углов ориентации ЛА на вертикальных траекториях полета | 2017 |
|
RU2671291C1 |
| СПОСОБ ПОВЫШЕНИЯ ТОЧНОСТИ НАВЕДЕНИЯ ДОВОДОЧНЫХ СТУПЕНЕЙ РАЗЛИЧНОГО НАЗНАЧЕНИЯ | 2010 |
|
RU2440557C9 |
| Способ определения ориентации объекта в бесплатформенной инерциальной навигационной системе | 2022 |
|
RU2794283C1 |
| Адаптивный способ коррекции углов ориентации БИНС | 2020 |
|
RU2754396C1 |
| Способ коррекции углов ориентации БИНС | 2022 |
|
RU2796328C1 |
| СПОСОБ ИНЕРЦИАЛЬНОГО АВТОСОПРОВОЖДЕНИЯ ЗАДАННОГО ОБЪЕКТА ВИЗИРОВАНИЯ И СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2011 |
|
RU2498193C2 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛОВ ИНЕРЦИАЛЬНОГО ПЕЛЕНГОВАНИЯ ЗАДАННОГО ОБЪЕКТА ВИЗИРОВАНИЯ И ИНЕРЦИАЛЬНЫЙ ДИСКРИМИНАТОР СИГНАЛОВ ПЕЛЕНГОВАНИЯ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2442185C2 |
| Способ коррекции углов ориентации БИНС на скользящем интервале | 2022 |
|
RU2790076C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ УПРАВЛЯЕМЫХ ПОДВИЖНЫХ ОБЪЕКТОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2003 |
|
RU2241959C1 |
Способ определения углового положения подвижного объекта относительно центра масс, т.е определение пространственной ориентации при угловом движении, преимущественно летательных аппаратов (ЛА), относительно какой-либо базовой системы координат, путем аналитического ее вычисления на основе измерений каких-либо отдельных параметров ориентации (углов, угловых скоростей и т.д.). Способ включает определение текущей угловой ориентации системы координат OX1Y1Z1 относительно геоцентрической базовой системы координат OXYZ, задание требуемой ориентации системы координат OX2Y2Z2 относительно геоцентрической базовой системы координат OXYZ, при этом системы координат OX1Y1Z1 и OX2Y2Z2 имеют начало координат в центре масс объекта и связаны с ним. Текущие значения углов ориентации связанной системы координат относительно базовой определяются с помощью бесплатформенной инерциальной навигационной системы (БИНС), при этом в геоцентрической базовой системе координат направление оси OZ принимают совпадающим с направлением вектора вращения Земли, а ось ОХ направлена в точку пересечения гринвичского меридиана с экватором. Определяют углы относительной ориентации ςx, ςy, ςz между соответствующими осями связанной системы текущей угловой ориентации и требуемой в геоцентрической базовой системе координат по определенным зависимостям и по результатам вычислений судят об угловом положении подвижного объекта. Технический результат - расширение области применения, повышение достоверности и точности определения углового положения подвижного объекта. 2 ил.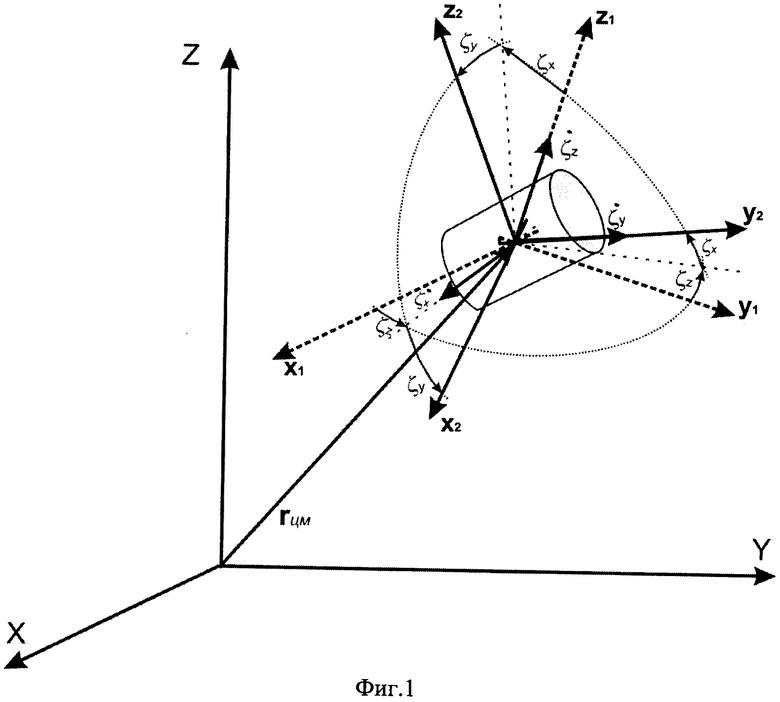
Способ определения углового положения подвижного объекта относительно центра масс, включающий определение текущей угловой ориентации системы координат OX1Y1Z1 с началом координат в центре масс объекта, связанной с подвижным объектом, относительно геоцентрической базовой системы координат OXYZ, задание требуемой угловой ориентации системы координат, определение текущих значений углов ориентации связанной системы координат относительно базовой, перевод связанной системы координат из текущей угловой ориентации в требуемую с последующим вычислением параметров, по которым судят об угловом положении подвижного объекта, отличающийся тем, что задают требуемую угловую ориентацию системы координат OX2Y2Z2, связанную с подвижным объектом, с началом координат в центре масс объекта, а параметрами, по которым судят об угловом положении подвижного объекта, являются углы относительной ориентации ζx, ζy, ζz между соответствующими осями связанной системы текущей угловой ориентации и требуемой в геоцентрической базовой системе координат, для чего определение текущих значений углов ориентации собственной системы координат подвижного объекта относительно геоцентрической базовой системы координат производят с помощью бесплатформенной инерциальной навигационной системы (БИНС), в геоцентрической базовой системе направление оси OZ принимают совпадающим с направлением вектора вращения Земли, а ось ОХ направлена в точку пересечения гринвичского меридиана с экватором, причем при переводе связанной системы координат из текущей угловой ориентации в требуемую принимают, что требуемая угловая ориентация связанной системы координат относительно геоцентрической базовой системы координат является неподвижной, саму требуемую связанную систему координат OX2Y2Z2 считают инерциальной и дальнейший процесс вычисления параметров осуществляют относительно этой неподвижной системы координат, углы относительной ориентации ζx, ζy, ζz определяют по следующим зависимостям:
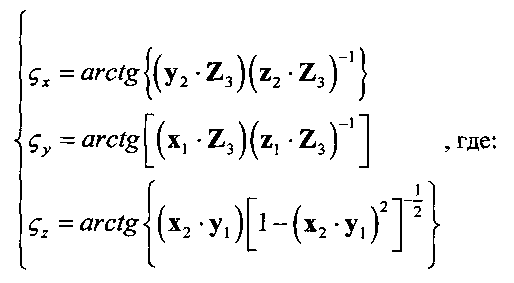
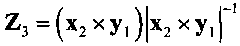 - промежуточная ось между OZ1 и OZ2;
- промежуточная ось между OZ1 и OZ2;
 ,
, 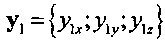 ,
, 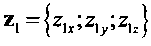 - оси текущей связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат;
- оси текущей связанной системы координат подвижного объекта в проекциях на оси геоцентрической базовой системы координат;
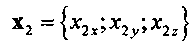 ,
, 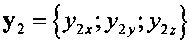 ,
, 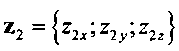 - оси требуемой связанной системы координат подвижного объекта в проекциях на оси геоцентрической инерциальной системы координат.
- оси требуемой связанной системы координат подвижного объекта в проекциях на оси геоцентрической инерциальной системы координат.
| СЕРЕГИН В.В "ПРИКЛАДНАЯ ТЕОРИЯ И ПРИНЦИПЫ ПОСТРОЕНИЯ ГИРОСКОПИЧЕСКИХ СИСТЕМ" УЧЕБНОЕ ПОСОБИЕ | |||
| - СПБ.: СПБГУ ИТМО, 2007; | |||
| СПОСОБ И УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ ВЕЛИЧИНЫ И НАПРАВЛЕНИЯ СМЕЩЕНИЯ ЦЕНТРА МАСС АППАРАТА | 2000 |
|
RU2176810C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВ ОРИЕНТАЦИИ ПОДВИЖНОГО ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2273826C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОРИЕНТАЦИИ АКСЕЛЕРОМЕТРОВ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2005 |
|
RU2289101C1 |
Авторы
Даты
2016-07-10—Публикация
2015-05-08—Подача