Изобретение относится к области автоматизации и управления и может быть использовано в динамических системах автоматического управления (САУ), автоматически выбирающих оптимальный режим работы для достижения предельного быстродействия, в частности в системах позиционно-следящего управления электроприводами технологических установок, в которых управляющее воздействие в процессе отработки задающих воздействий требует ограничения на предельно допустимом уровне.
Известны способы дискретного управления линейными объектами с подчиненным (каскадным) регулированием его переменных и ограничением управления каждой из подчиненных переменных путем ограничения сигналов, формируемых регулятором старшего контура управления [Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: учеб. пособие для вузов. - Л.: Энергоиздат. Ленингр. отд-е, 1982. - 392 с.].
Недостатком известных способов является значительное снижение быстродействия старшего контура управления, причем в геометрической прогрессии от числа подчиненных контуров управления. В результате, например для позиционно-следящих систем управления, содержащих два и более подчиненных контуров управления, быстродействие старшего контура снижается в несколько раз.
Известны способы дискретного финитного управления по состоянию объекта управления на основе контроля его полного состояния и задающих воздействий, в том числе на основе применения наблюдающих устройств, запоминания информации об этих переменных на шаге дискретного управления и выработки оптимального дискретного управляющего воздействия в функции контролируемых переменных [Ковчин С.А., Хаммами А.К. Анализ проблем построения цифровых финитных регуляторов и методы ограничения их выходных сигналов / В кн. Вычислительные, измерительные и управляющие системы. Труды СПбГТУ. №468-СПб, 1997 - С. 3-8].
Недостатком указанных способов является появление перерегулирования выходной переменной при ограничении управления на допустимом уровне, т.к. методология синтеза финитных регуляторов состояния ориентирована на класс линейных САУ, а ограничение управляющего воздействия требует применения в структуре замкнутой САУ нелинейного звена типа «насыщение» и, как следствие, ведет к появлению проблем обеспечения устойчивости и качества нелинейных систем управления.
Наиболее близким по технической сущности к заявляемому изобретению является способ управления линейным объектом с ограничением управления, основанный на модельном прогнозировании, при котором на каждом шаге (периоде) дискретного управления, меньшем горизонта управления, измеряют или оценивают переменные состояния объекта и аддитивные, в частности, задающие воздействия, принадлежащие соответствующим ограниченным множествам значений этих переменных, запоминают их на шаге управления, решают задачу оптимизации управления на ограничениях величины управления и формируют управляющее воздействие на объект [Гудвин Г.К., Гребе С.Ф., Сальгадо М.Э. Проектирование систем управления. - М.: БИНОМ. Лаборатория знаний, 2010,911 с.].
Недостатком указанного способа является формирование прогнозирующего ограниченного управления с постоянным шагом (периодом) дискретного управления, являющимся методологической основой этого способа управления, что не позволяет реализовать предельное быстродействие линейных САУ при ограничении управления на допустимом уровне, причем достигаемое лишь на одном из шагов прогнозируемых программных траекторий.
Технический результат изобретения заключается в обеспечении предельного быстродействия отработки системой произвольного начального состояния объекта управления и изменения аддитивных воздействий, в частности, задающего воздействия выходной переменной САУ.
Указанный технический результат достигается тем, что в способе дискретного управления линейным объектом с ограничением управления, основанном на применении модельного прогнозирующего управления, при котором на каждом шаге (периоде) дискретного управления, меньшем горизонта управления, измеряют или оценивают переменные состояния объекта и внешние, в частности, задающие воздействия, принадлежащие соответствующим ограниченным множествам, запоминают их оценки с применением экстраполяторов нулевого порядка и формируют ограниченное по величине прогнозирующее управляющее воздействие на объект, причем на каждом шаге дискретного управления решают задачу однопараметрической оптимизации величины периода финитного управления на ограничениях максимального значения управляющего воздействия и минимально допустимого периода управления на горизонте управления, что позволяет реализовать достижение максимально допустимого уровня управления на каждых п последующих прогнозируемых шагах горизонта управления. При этом производят параметрическую настройку параметров финитного регулятора как нелинейных функций полученного оптимального периода финитного управления, а минимальное значение периода управления выбирают не менее периода, обеспечивающего на горизонте управления заведомое вхождение системы управления в линейную зону работы на всех множествах значений переменных состояния и внешних аддитивных воздействий.
Отличительным признаком предлагаемого способа управления является то, что шаг (период) дискретного управления принят в качестве переменного параметра самонастройки системы, обеспечивающим такие значения параметров регулятора на каждом шаге дискретного управления, что прогнозное финитное управление достигает предельно допустимого значения на каждом горизонте управления.
Важно, что финитное управление обладает таким свойством, что переводит систему из любого начального состояния Х(0) в начало координат Х(n)=0 за заданное фиксированное время nT, где n - порядок линейного объекта управления. Если допустить, что на одном из n шагов прогнозирующего управления достигается ограниченное по величине управление, то этот шаг может рассматриваться как один из шагов финитного управления линейным объектом без ограничения. Поскольку прогнозируемое значение периода на каждом последующем шаге управления для любых асимптотически устойчивых САУ, к которым относятся системы финитного управления, имеет тенденцию к уменьшению интегральной квадратической ошибки управления, то и время переходного процесса тоже имеет тенденцию к снижению, а, следовательно, ведет к увеличению быстродействия САУ.
Кроме того, еще одним отличительным признаком предлагаемого решения является следующее. В соответствие с предлагаемым способом период управления неизбежно стремится к нулю при уменьшении переменных состояния объекта управления в процессе финитного управления. Для ограничения периода управления снизу предлагается в модель оптимизатора ввести минимальное значение Тмин, определяемое из условия обеспечения вхождения САУ в линейную зону работы на всех множествах значений переменных состояния и задающих воздействий на горизонте управления.
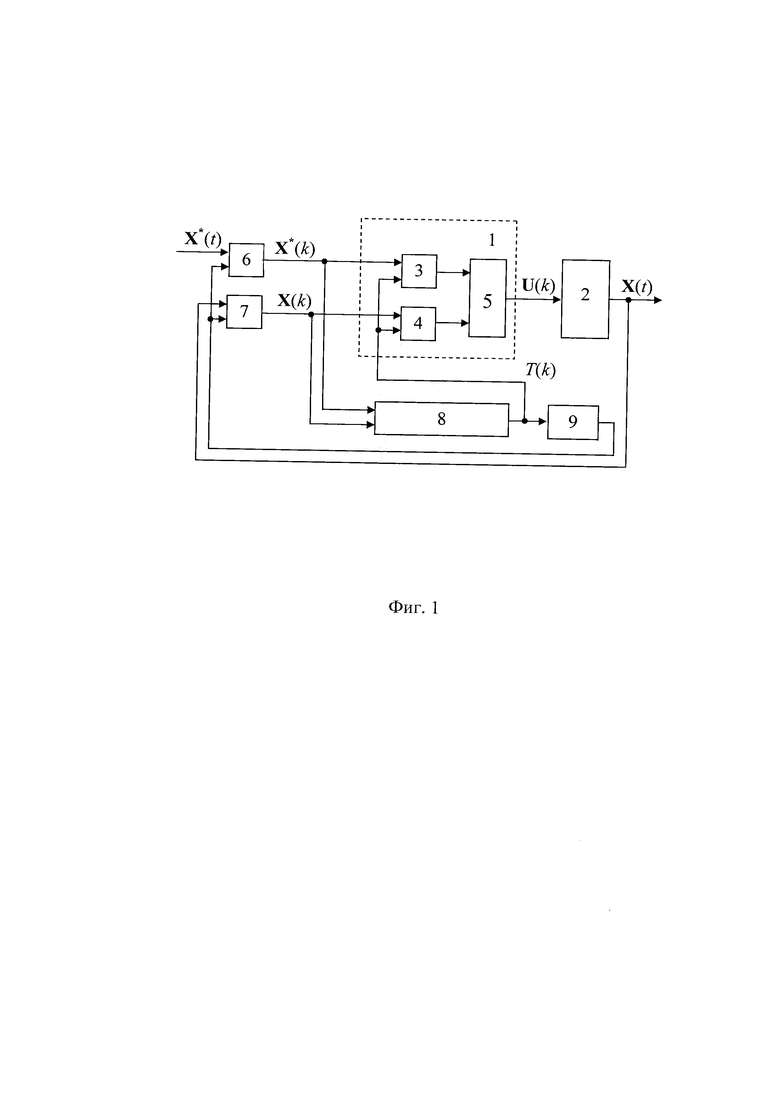
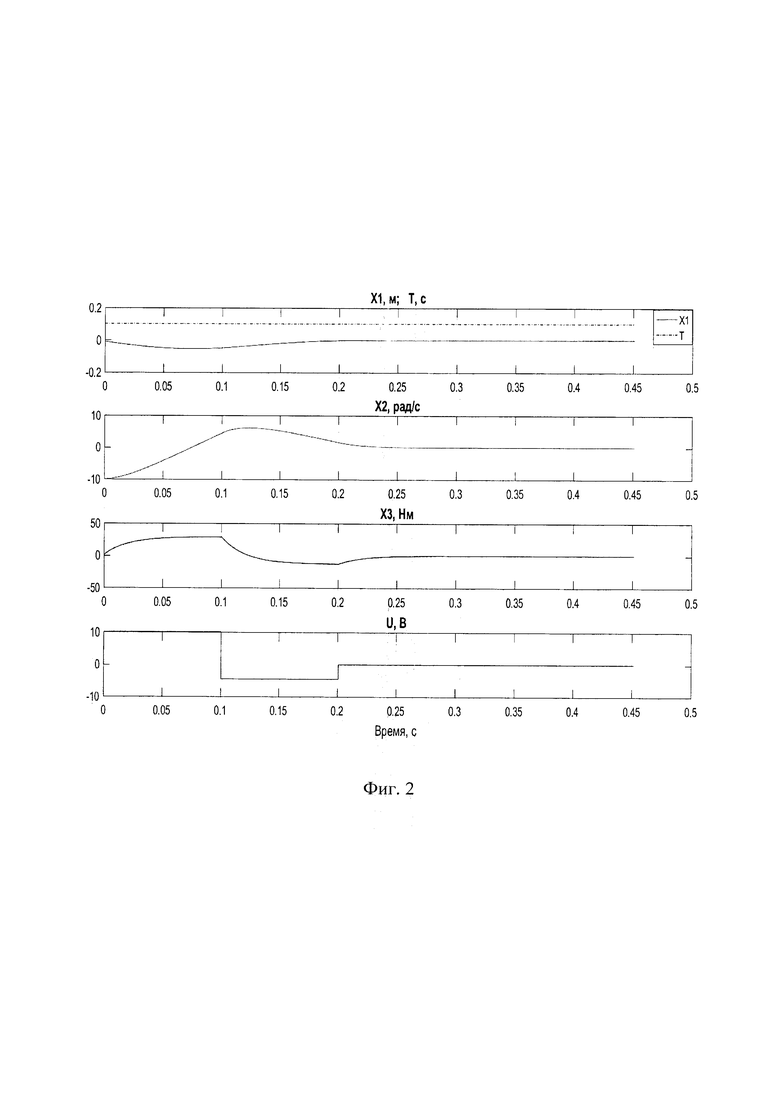
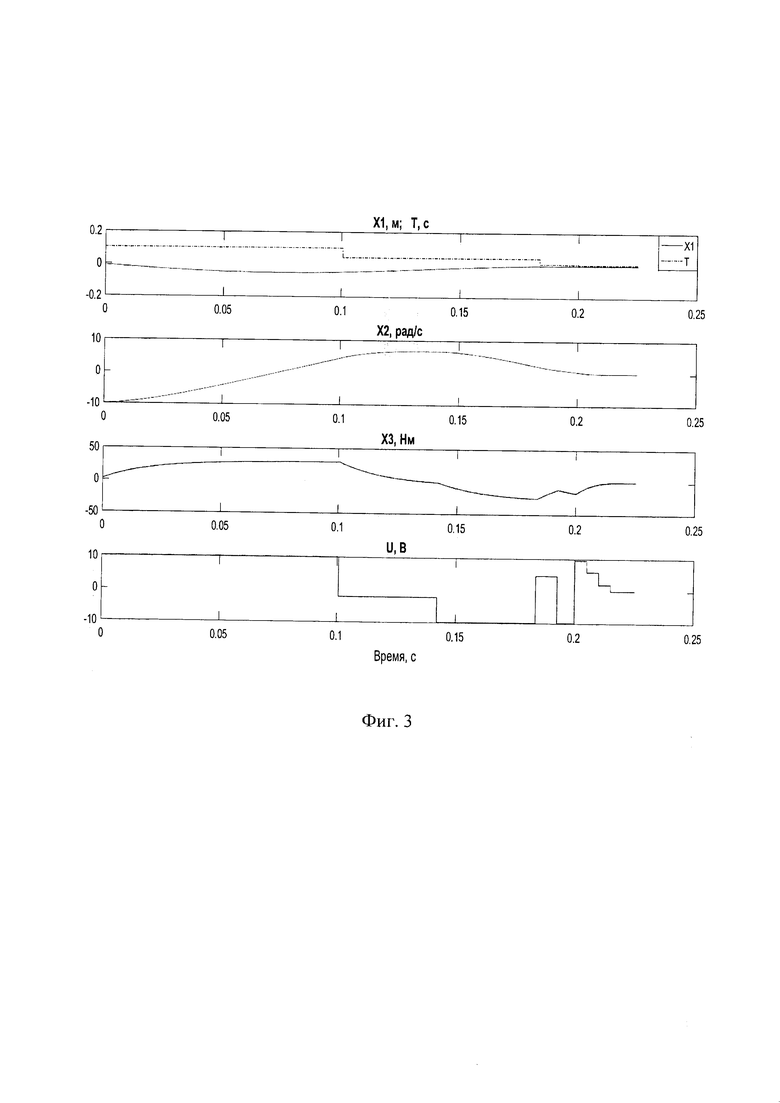
На фиг 1. приведена функциональная схема устройства, реализующего предложенный способ; на фиг. 2 - кривые переходных процессов при отработке ненулевых начальных условий Х(0) состояния объекта и тестового ступенчатого воздействия X*(t)=const на САУ в соответствие со способом-прототипом; на фиг. 3 - кривые переходных процессов при отработке ненулевых начальных условий Х(0) состояния объекта и тестового ступенчатого воздействия X*(t)=const на САУ в соответствие с предложенным способом. Переменные X1, Х2, Х3 и управление U на рисунках соответствуют переменным рассматриваемого ниже примера устройства для реализации предложенного способа управления.
Устройство, реализующее способ (фиг. 1), состоит из последовательно включенных регулятора 1 и объекта 2 управления, причем регулятор 1 содержит модули 3 и 4 параметрической самонастройки, выходы которых подключены к входам сумматора 5, выход которого подключен к входу объекта 2 управления. Информационные входы (верхние по схеме) модулей 3 и 4 самонастройки регулятора 1 соединены соответственно с выходами экстраполяторов 6 и 7 нулевого порядка, а входы самонастройки (нижние по схеме) объединены и соединены с выходом модуля оптимизатора 8 и с входом импульсного модулятора 9. Первый и второй входы оптимизатора 8 подключены соответственно к выходам экстраполяторов 6 и 7. На информационный вход (верхний по схеме) экстраполятора 6 подано аддитивное задающее воздействие САУ, на информационный вход (верхний по схеме) экстраполятора 7 нулевого порядка подана информация о текущем состоянии объекта управления. Выход импульсного модулятора 9 соединен с входами синхронизации выборки информации экстраполяторов 6 и 7.
Устройство, реализующее способ, работает следующим образом.
В некоторый начальный момент времени t в экстраполяторах 6 и 7 по синхросигналу импульсного модулятора запоминается информация о задающем воздействии Х*(t) и текущем состоянии X(t) переменных САУ. Экстраполяторы нулевого порядка (в англ. интерпретации - «Zero Order Hold») реализуются либо на основе устройств выборки-хранения (УВХ) при использовании аналоговой информации о переменных объекта управления, либо на основе регистров памяти при цифровой информации об этих переменных.
На основе этой информации оптимизатор 8 решает задачу однопараметрической оптимизации T(X*(t), X(t), U(k), k) → Topt(k) на условиях ограничения управления Umin≤U(k)≤Umax и минимально допустимого периода оптимального управления Topt(k)≥Tmin. Вопросы условной однопараметрической оптимизации в литературе по теории управления и оптимизации теоретически хорошо проработаны и решаются, в основном методами деления отрезка пополам, дихотомии и золотого сечения.
Полученное оптимизатором 8 оптимальное значение периода Topt(k) финитного управления подается на адаптивный регулятор 1, а именно на входы его самонастройки. Это позволяет параметрам финитного регулятора на каждом шаге финитного управления изменяться таким образом, что управляющее воздействие U(k) на его выходе в соответствие с модельным прогнозирующим управлением на горизонте управления, равном n⋅Topt, не будет превышать заданные оптимизатором ограничения Umin≤U(k)≤Umax. Смена дискретных значений Х*(k), Х(k) в параметрах самонастройки адаптивного регулятора 1 осуществляется по синхросигналам импульсного модулятора 9, формирующего частотно-импульсную последовательность с оптимальным периодом Topt(k) следования импульсов, рассчитанным оптимизатором 8. Таким образом, импульсный модулятор 9 представляет собой типовой преобразователь «код - частота следования импульсов». Объект управления 2 отрабатывает дискретное управление U(k), сформированное регулятором 1 на каждом шаге финитного управления, обеспечивая минимальное время переходного процесса и ограниченное по величине управление. При этом на каждом k-м шаге горизонт управления всегда равен n шагов, но величина шага (периода) меняется оптимизатором 8 в зависимости от начальных условий и аддитивных воздействий, в частности, задающего воздействия, на каждом из этих шагов.
В качестве примера, иллюстрирующего эффективность предложенного подхода, рассмотрим способ управления электромеханическим объектом, представленном векторно-матричным дискретно-непрерывным уравнением в концепции линейных систем управления (в англ. интерпретации «Linear Time Invariance» - LTI):
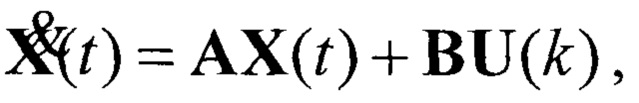
где Х(t), U(k) - векторы состояния и дискретного управления, действующего на объект управления, размера соответственно n×1 и 1×1; А, В - матрицы постоянных коэффициентов размера n×n, n×m соответственно,
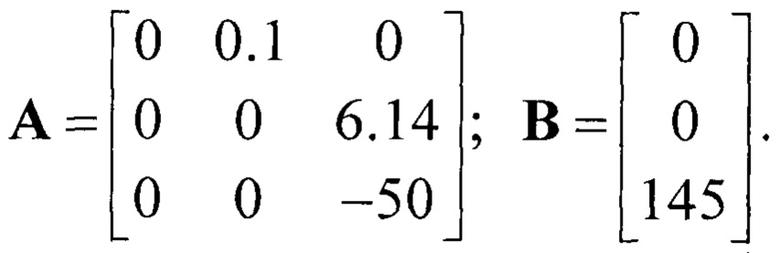
Такая модель объекта соответствует последовательно включенным апериодическому звену (контура регулирования момента) и двум интегрирующим звеньям (электромеханическая часть позиционного привода).
Финитное управление объектом имеет вид:
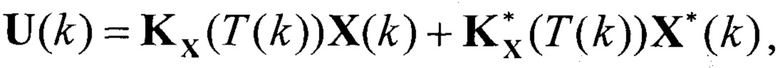
где k - номер такта дискретного финитного управления с изменяемым периодом, k∈(1, ∞); U(k)=U(k) - скалярное управление; KX(Т(k)) - матрица-строка размера 1×3 изменяющихся во времени по сигналам импульсного модулятора коэффициентов финитного регулятора, отвечающая за адаптивное финитное свободное движение; Т(k) - период дискретного управления, меняющийся в k-е моменты времени выработки управления и формируемый оптимизатором 8; Х(k) - фактическое значение компонент вектора состояния в k-й момент времени дискретного управления на выходе экстраполятора 7, полученных на основе измерения или наблюдения переменных состояния объекта управления, 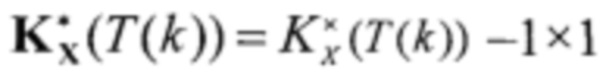 переменный во времени коэффициент, отвечающий за оптимальное вынужденное движение САУ под действием аддитивного задающего воздействия; X*(k)=S*(k) - заданное значение выходной переменной САУ - позиции рабочего органа, сформированное в k-й момент времени на выходе экстраполятора 6.
переменный во времени коэффициент, отвечающий за оптимальное вынужденное движение САУ под действием аддитивного задающего воздействия; X*(k)=S*(k) - заданное значение выходной переменной САУ - позиции рабочего органа, сформированное в k-й момент времени на выходе экстраполятора 6.
Для рассматриваемой модели электромеханического объекта имеем: Х(k)=[х1(k), х2(k), …, х3(k)]Т=[S(k), V(k), M(k)T, где S(k), ω(k), М(k) - соответственно положение (м) рабочего органа, скорость вращения вала электропривода (рад/с) и момент (Нм) на валу привода.
Переменные состояния объекта управления и управляющее воздействие образуют соответствующие замкнутые множества.
Зададимся условиями имитационного моделирования для сравнительного анализа способа-прототипа и предлагаемого решения. Пусть переменные электромеханической САУ (положение рабочего органа, скорость вращения вала и момент на валу привода) имеют конкретные начальные значения: начальная позиция Х1(0)=-0.01 (м), начальная скорость Х2(0)=-10 рад/с, начальный момент на валу привода, определяемый нагрузкой на валу, Х3(0)=1 Н⋅м. Не снижая общности результатов, зададимся нулевой конечной позицией, т.е. X*=S*=0 (м). Для определенности зададимся также ограничением управляющего воздействия |U(k)|=Umax(k)=10 В и минимально допустимым значением периода управления Tmin=0,005 с. Число шагов (горизонт управления) в соответствие с принципом финитного управления n=3, т.е. порядку объекта управления.
На фиг. 2 приведены результаты модельного прогнозирующего управления, реализуемого с применением способа-прототипа, при котором рассчитан оптимальный шаг (период) Т(k) ≈ 0,1 с, а время регулирования (полного установления финитного процесса управления) составляет 0,3 с. Заметим, что в процессе управления минимально допустимое значение периода здесь не достигается, шаг управления остается неизменным в течение всего горизонта управления, а процессы имеют апериодический характер, теоретически длящийся бесконечно долго.
На фиг. 3 приведены результаты модельного прогнозирующего управления, реализуемого с применением предложенного способа при тех же начальных значениях переменных и задающего воздействия. В этом случае шаг (период) уменьшается в процессе управления, т.е. T(k)=var, причем установление переходных процессов реализуется в линейной зоне работы САУ при достижении минимально возможного периода управления, т.е. T(k)=Tmin=0.005 с. Хотя число шагов и увеличилось, но время регулирования (полного установления процесса управления) уменьшилось и составляет порядка 0,215 с. При этом после вхождения САУ в зону линейного финитного управления, т.е. при работе с минимальным периодом Tmin, реализуется теоретически конечное время установления процесса ровно за n⋅Tmin=0.015 с. Это особенно важно, когда позиционирование рабочего органа объекта управления реализуется максимально быстро в микрометровом диапазоне и не допускает режима «дотягивания».
Как видим, применение предложенного способа дискретного управления с ограничением управляющего воздействия позволяет за счет оптимизации периода прогнозирующего управления на каждом шаге прогноза повысить быстродействие САУ и решить поставленную задачу повышения быстродействие САУ при ограничениях управления. Сопутствующим эффектом является повышение точности функционирования САУ в установившемся режиме вследствие реализации минимального допустимого периода отработки изменений переменных.
Источники информации
1. Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами: учеб. пособие для вузов. - Л.: Энергоиздат. Ленингр. отд-е, 1982. - 392 с.
2. Ковчин С.А., Хаммами А.К. Анализ проблем построения цифровых финитных регуляторов и методы ограничения их выходных сигналов. / В кн. Вычислительные, измерительные и управляющие системы. Труды СПбГТУ. №468-СПб, 1997 - С. 3-8.
3. Гудвин Г.К., Гребе С.Ф., Сальгадо М.Э. Проектирование систем управления. - М.: БИНОМ. Лаборатория знаний, 2010, 911 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для управления движениемплАВучЕгО СЕйСМОРАзВЕдОчНОгО КОМплЕКСА | 1978 |
|
SU842724A1 |
| УСТРОЙСТВО ДЛЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ПРОЦЕССОМ ДРОБЛЕНИЯ МАТЕРИАЛА | 2001 |
|
RU2204438C1 |
| Система управления движением судна | 1978 |
|
SU717730A1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ | 2016 |
|
RU2616219C1 |
| СИСТЕМА (ВАРИАНТЫ) И СПОСОБ ДЛЯ УПРАВЛЕНИЯ ПЕРЕКЛЮЧЕНИЕМ ПЕРЕДАЧ ТРАНСПОРТНОГО СРЕДСТВА В РЕЖИМЕ КРУИЗ-КОНТРОЛЯ | 2017 |
|
RU2748955C2 |
| ОПТИМИЗИРОВАННОЕ ИНТЕГРИРОВАННОЕ УПРАВЛЕНИЕ ДЛЯ ЭЛЕКТРОСТАНЦИИ, РАБОТАЮЩЕЙ НА СЖИГАНИИ КИСЛОРОДНОГО ТОПЛИВА | 2011 |
|
RU2559416C2 |
| УСТРОЙСТВО ДЛЯ УПРАВЛЕНИЯ ПРОЦЕССОМ ИЗГОТОВЛЕНИЯ БЕТОННЫХ И ЖЕЛЕЗОБЕТОННЫХ ИЗДЕЛИЙ | 1994 |
|
RU2082606C1 |
| Адаптивная система управления | 1983 |
|
SU1174903A1 |
| ПАРАМЕТРИЧЕСКИЙ СИНТЕЗАТОР | 1970 |
|
SU265218A1 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ | 2013 |
|
RU2541848C1 |
Изобретение относится к способу дискретного управления линейным объектом с ограничением управления. Применяют модельное прогнозирующее управление, при котором на каждом шаге дискретного управления, меньшем горизонта управления, измеряют или оценивают переменные состояния объекта и внешние, в частности, задающие воздействия, принадлежащие соответствующим ограниченным множествам, запоминают их оценки с применением экстраполяторов нулевого порядка и формируют ограниченное по величине прогнозирующее управляющее воздействие на объект определенным образом, обеспечивая заведомое вхождение системы управления в линейную зону работы на всех множествах значений переменных состояния и внешних воздействий. Обеспечивается предельное быстродействие отработки системой произвольного начального состояния объекта управления и изменение аддитивных воздействий, в частности задающего воздействия выходной переменной САУ. 3 ил.
Способ дискретного управления линейным объектом с ограничением управления, основанный на применении модельного прогнозирующего управления, при котором на каждом шаге дискретного управления, меньшем горизонта управления, измеряют или оценивают переменные состояния объекта и внешние, в частности, задающие воздействия, принадлежащие соответствующим ограниченным множествам, запоминают их оценки с применением экстраполяторов нулевого порядка и формируют ограниченное по величине прогнозирующее управляющее воздействие на объект, отличающийся тем, что на каждом шаге дискретного управления решают задачу однопараметрической оптимизации величины периода финитного управления на ограничениях максимального значения управляющего воздействия и минимально допустимого периода управления на горизонте управления, при этом производят параметрическую настройку параметров финитного регулятора как нелинейных функций полученного оптимального периода финитного управления, а минимальное значение периода управления выбирают не меньше периода, обеспечивающего на горизонте управления заведомое вхождение системы управления в линейную зону работы на всех множествах значений переменных состояния и внешних воздействий.
| Квазиинвариантный финитный регулятор с переменной структурой | 1986 |
|
SU1385123A1 |
| Приемный барабан чесальной машины | 1947 |
|
SU80970A1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ КОМПЕНСАЦИИ ВЛИЯНИЯ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ МОМЕНТА НАГРУЗКИ В ЭЛЕКТРОМЕХАНИЧЕСКОЙ СИСТЕМЕ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2014 |
|
RU2576594C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 1999 |
|
RU2150728C1 |
| Способ получения матовых глазурей для керамических плиток | 1985 |
|
SU1320184A1 |
Авторы
Даты
2020-08-07—Публикация
2019-12-26—Подача