Изобретение относится к измерительной технике в машиностроении и на транспорте. Оно может быть использовано для определения положения центра тяжести массивного и крупногабаритного объекта (изделия) путем его подвешивания при помощи подъемного устройства. В частности, оно может быть использовано для обеспечения безопасной погрузки/выгрузки на судно тяжеловесных и крупногабаритных грузов, так как неточное позиционирование последних относительно системы подвешивания зачастую приводит к разного рода инцидентам вплоть до опрокидывания или обрыва груза.
Изобретение может найти применение в других отраслях промышленности при проектировании, постройке или транспортировке сложных конструкций (летательных и подводных аппаратов, объектов энергетики, судо- и самолетостроения и проч.), везде, где чрезвычайно важно умение определять достаточно быстро и без значительных затрат положения центра тяжести объекта.
Известен способ определения центра тяжести массивных и крупногабаритных объектов, заключающийся в том, что объект через промежуточную траверсу и стропы (петлю навески) присоединяют к крюку подъемного устройства, после чего осуществляют подъем груза с опиранием его одной стороной, замеряют усилие, действующее на крюк подъемного устройства, из условия равновесия груза (объекта) при его одностороннем опирании определяют расстояние от точки подвеса до приблизительного месторасположения центра тяжести груза, перемещают петлю навески траверсы на это расстояние по направлению к этому месторасположению центра тяжести груза и последовательно повторяют этот процесс до точного совмещения петли подвески траверсы с центром тяжести груза [1]. Однако, данный способ достаточно сложен в реализации, так как перед каждым последующим подвешиванием необходимо перемещать объект относительно точки подвеса (крюка грузового устройства), для чего необходимо иметь достаточно сложный механизм перемещения (промежуточный подвижный элемент, соединенный с рамой траверсой). Кроме того, рама траверсы имеет специальные сложные захваты для груза (объекта), при этом форма поверхности объекта в местах захвата не может быть произвольной, или для каждого отдельного груза (имеющего другую форму) необходимо иметь свои специфические захваты. Наконец, для определения положения центра тяжести (ЦТ) груза необходимо каждый раз не только контролировать пространственную ориентацию полу-подвешенного объекта, но и измерять силу, действующую на крюк подъемного устройства, что также усложняет механизм и процедуру определения ЦТ.
Наиболее близким техническим решением является способ определения положения центра тяжести (ЦТ) массивных и крупногабаритных объектов сложной формы заключающийся в присоединении объекта (с помощью двух групп гибких строп) через промежуточную прямоугольную траверсу к крюку подъемного устройства, многократном (не менее двух) поднятии и свободном подвешивании объекта до положения равновесия с разной пространственной ориентацией, измерении параметров ориентации объекта в подвешенном положении равновесия и последующем вычислении на их основе координат ЦТ объекта [2]. Однако этот способ так же не лишен недостатков. Во-первых, измерение пространственной ориентации объекта и последующая процедура расчета координат его ЦТ достаточно сложна. Это обусловлено тем, что вторичные стропы (присоединяющие объект к траверсе) имеют неодинаковую длину, при этом они в подвешенном положении системы могут иметь разные углы отклонения от вертикали. Поэтому процедура расчета ЦТ сложна и громоздка с большим количеством уравнений и формул. Во-вторых, и это более существенно, если вторичные стропы присоединить к грузу (объекту) не в его верхней части (например, в средине или внизу), то вся система после ее подвешивания может стать неустойчивой. В этом случае груз может опрокинуться со всеми вытекающими негативными последствиями.
Замечание 1. Подвешивание тяжеловесного или крупногабаритного груза путем закрепления строп подъемного устройства в верхней части этого груза на практике бывает редко. Большинство таких грузов (объектов), состоят из многих отдельных элементов, и для подвешивания, как правило, не предназначены. Поэтому, для их транспортировки к месту постоянного использования, они устанавливаются на специальную погрузочную (транспортировочную) платформу, в которой и предусматриваются места (точки) крепления погрузочных строп. То есть, подвешивание (подъем) таких грузов осуществляется за счет крепления строп подъемного устройства в нижней части груза со всеми возможными негативными последствиями для устойчивости.
Цель изобретения - обеспечение устойчивости системы подвешивания, недопущение опрокидывания и повреждения объекта, упрощение процедуры измерения и расчета положения его центра тяжести (ЦТ). Поставленная цель достигается тем, что первичные стропы (соединяющие траверсу и крюк подъемного устройства) выбирают одинаковой длины (l) и таковой, чтобы подвешиваемый (измеряемый) объект мог быть вписан внутрь пирамиды, образованной траверсой и этими стропами, вторичные стропы (соединяющие объект и траверсу) также выбирают равной длины и присоединяют к объекту и траверсе таким образом, чтобы они были вертикальны и параллельны друг другу, при каждом подвешивании (измерении) разную пространственную ориентацию объекта в положении равновесия обеспечивают за счет изменения длины первичных строп  а саму эту ориентацию определяют с помощью измерения углов отклонения (αi и βi) от начального (горизонтального) положения сторон прямоугольника, образованного точками крепления вторичных строп к объекту (или погрузочной платформе, на которой установлен и закреплен последний), после чего вычисляют вертикальную координату центра тяжести (z) объекта по одной из следующих формул:
а саму эту ориентацию определяют с помощью измерения углов отклонения (αi и βi) от начального (горизонтального) положения сторон прямоугольника, образованного точками крепления вторичных строп к объекту (или погрузочной платформе, на которой установлен и закреплен последний), после чего вычисляют вертикальную координату центра тяжести (z) объекта по одной из следующих формул:

или:

а затем вычисляют поперечную (х) и продольную (у) координаты центра тяжести объекта по формулам:

где Рс, р - вес (масса) объекта и траверсы, Н (кг);
 - высота пирамиды первичного подвеса при i-том подвешивании, м;
- высота пирамиды первичного подвеса при i-том подвешивании, м;
а, b - длина и ширина траверсы, м;
 - длина первичных строп при i-м подвешивании, м;
- длина первичных строп при i-м подвешивании, м;
αi, βi - углы отклонения объекта (погрузочной платформы) от горизонтали при i-том подвешивании, град.
Технический результат изобретения достигается тем, что, во-первых, длину первичных строп (высоту пирамиды первичного подвеса) выбирают таковой, чтобы обеспечить устойчивость системы подвешивания с грузом (объектом) в положении равновесия; во-вторых, изменение пространственной ориентации объекта от опыта к опыту обеспечивают изменением длины первичных строп (и соответственно, высоты пирамиды первичного подвеса), в-третьих, при каждом опыте (подвешивании) длину как первичных, так и вторичных строп выбирают одинаковой, при этом, вторичные стропы закрепляют на траверсе и грузе (погрузочной платформе) параллельно друг другу, в-четвертых, в каждом опыте (подвешивании) измеряют углы отклонения объекта от исходного (до подвешивания) положения, после чего вычисляют координаты центра тяжести (ЦТ) объекта по формулам, отражающим причинно-следственные связи между массо-габаритными показателями системы подвешивания с объектом, углами отклонения объекта в подвешенном состоянии и координатами центра тяжести (ЦТ) последнего.
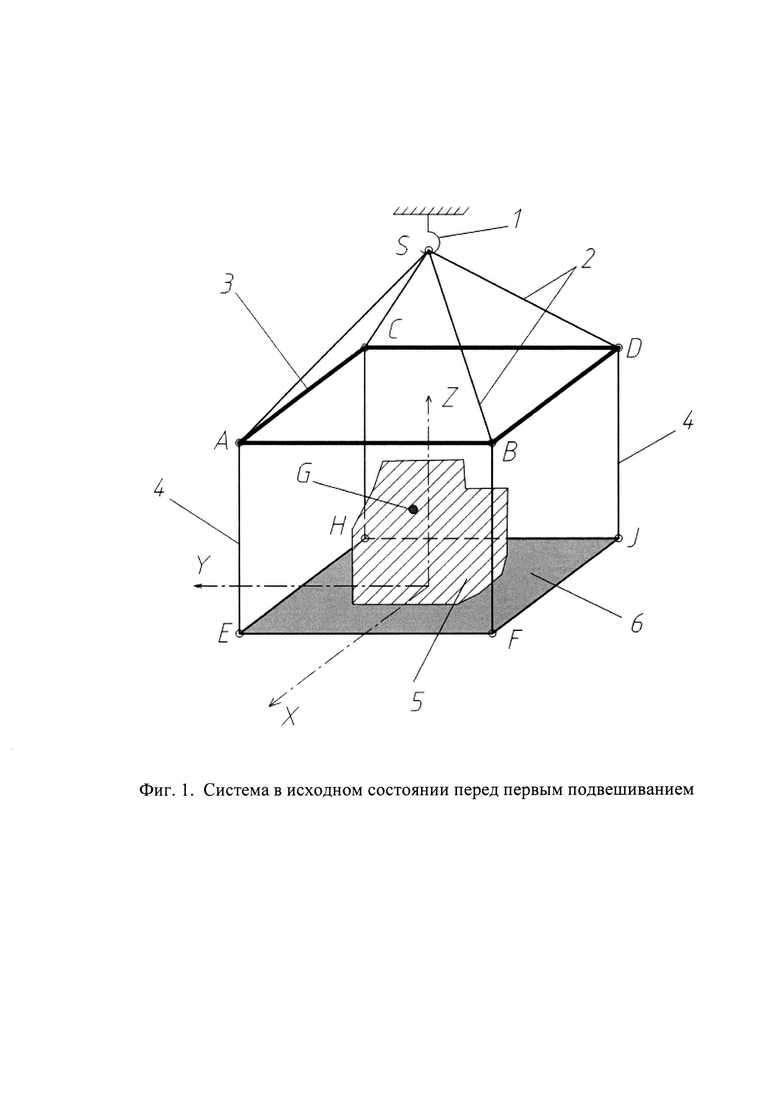
Некоторые дополнительные пояснения к заявляемому способу и формулам (1-4). Пусть имеется система подвешивания с грузом (объектом), представленная на фиг. 1 и состоящая из крюка подъемного устройства 1, соединенного посредством четырех первичных строп 2 с прямоугольной жесткой траверсой 3 (прямоугольник ABCD на фиг. 1), а также четырех вторичных строп 4, соединенных с траверсой 3 и грузом 5 (или его погрузочной платформой 6) в точках EFHJ. В работах [3-6] показано, что такая система после ее подвешивания на крюке 1 может принимать равновесное положение путем совместного отклонения траверсы 3 и объекта 5 от их первоначального положения. Это происходит вследствие того, что до подвешивания ЦТ груза (точка G) не находится на одной вертикали с точкой подвеса S (фиг. 1). Более того, при достаточно высоком положении ЦТ (относительно базы - плоскости, образованной точками крепления строп EFHJ к грузу 5 или его погрузочной платформе 6), такая двухзвенная система подвешивания может оказаться неустойчивой вплоть до нарушения целостности связей системы и опрокидывания груза (объекта) [3-6]. В работах [5, 6] подробно рассмотрены условия, при которых система, представленная на фиг. 1, становится неустойчивой после ее подвешивания. В частности, было показано, что для количественной оценки устойчивости такой пространственной системы ее необходимо вначале свести к двум плоским системам подвешивания (фиг. 2) путем проецирования на две вертикальные взаимно перпендикулярные плоскости, проходящие через точку подвеса S. Было также показано [5, 6], что для каждой из таких плоских систем необходимым и достаточным условием устойчивого равновесия является нахождение ЦТ груза (объекта), внутри равнобедренного треугольников EFTy (или FJTx - фиг. 2), названного авторами [5, 6] треугольникам безопасности. Основанием каждого из треугольников безопасности является база EF (FJ) (отрезок между нижними точками крепления вторичных строп). При этом, высота треугольников (zm=OTx=OTy) зависит от отношения масс (весов) траверсы и груза, а также высоты первичного подвеса (расстояния между точкой подвеса S и проекциями траверсы АВ (BD). В соответствии с [5, 6] высота каждого из треугольников безопасности (она будет одинаковой для обеих плоских систем-проекций) может вычислена по формуле

где h - высота первичного подвеса, вычисляемая по формуле:

где l - длина первичных строп, м;
a=AB=CD,b=BD=AC - длины сторон траверсы, м;
Рс, р - масса груза и траверсы, кг.
Поскольку вторичные стропы параллельны друг другу, то EF=AB=a и BD=FJ=b. Отсюда следует, что длина основания каждого треугольника безопасности (для ЦТ груза) равна длине соответствующей стороны траверсы. Кроме того, из формулы (5) видно, что высота треугольника безопасности равна или даже больше высоты первичного подвеса h (так как  ).
).
Таким образом, область безопасного положения ЦТ груза для устойчивости плоской системы определяется размерами треугольника безопасности с основанием, совпадающим с базой (EF или FJ) и высотой, равной или больше высоты первичного подвеса h [5, 6].
Логично предположить, что для большинства объектов ЦТ не может быть расположен за пределами их внешней (наружной) поверхности. Отсюда становится понятным, что если наружная поверхность объекта (или ее след на плоскости) вписывается внутрь треугольника безопасности, то устойчивость такой системы подвешивания гарантирована, о чем и заявляется в нашем изобретении.
Замечание 2. Если известно (хотя бы приблизительно) положение ЦТ груза (объекта) до измерения, то при формировании системы подвешивания и обеспечения ее устойчивости нет необходимости вписывать наружную поверхность объекта внутрь треугольника безопасности. Достаточно, чтобы предполагаемый ЦТ объекта находился внутри этого треугольника.
Возвращаясь от анализа устойчивости плоских систем к реальной (трехмерной) системе подвешивания, представленной на фиг. 1, логично предположить, что устойчивость последней будет обеспечена, если ЦТ груза расположить внутри области, ограниченной взаимным наложением (пересечением) двух призм, внешними гранями которых являются стороны двух треугольников безопасности EFTy и FJTx (фиг. 3). Очевидно, что эта область - ни что иное как пирамида EFHJT (фиг. 3), основанием которой является прямоугольник, эквивалентный базе EFHJ (или траверсы ABCD) и высота которой равна zm (фиг. 3), вычисляемая по формуле (5).
Теперь рассмотрим, как будет отклоняться (деформироваться) система с грузом в подвешенном положении равновесия, если ЦТ объекта изначально не находился на одной вертикали с точкой подвеса S. Для этого, вначале привяжем к нашей системе подвешивания систему координат, как показано на фиг. 1, 2, а именно: начало координат разместим в центре базы EFHJ, то есть на одной вертикали с точкой подвеса S. Ось OZ направим вертикально вверх, ось ОХ - горизонтально и параллельно отрезкам EH, FJ, и наконец, ось OY - горизонтально и параллельно отрезкам EF, HL (фиг. 1, 2). Условимся также, что система координат жестко связана с базой EFHJ, то есть при подвешивании и отклонении объекта система координат будет смещаться вместе с объектом и базой EFHJ.
Пусть координаты ЦТ груза равны x, y, z, при этом х и у не равны нулю, то есть первоначально (до подвешивания системы) ЦТ груза смещен относительно точки подвеса. Пусть также внешняя поверхность (предполагаемые координаты ЦТ) груза таковы, что находятся внутри пирамиды безопасности EFHJT. При таких условиях после подвешивания система будет находиться в устойчивом положении равновесия с некоторыми углами отклонения первичного подвеса (включая траверсу ABCD) и груза, при этом вторичные стропы останутся параллельны и вертикальны, что было показано и доказано в работах [5, 6]. В частности, отклонение траверсы и груза в плоскости ZOY произойдет на некоторый угол α, который можно вычислить по формуле [5, 6]:

В плоскости ZOX отклонение системы произойдет на угол β, который можно вычислить по аналогичной формуле:

Поскольку формулы (7) и (8) представляют собой систему уравнений, то их можно использовать для решения обратной задачи: по известным углам отклонения системы подвешивания α, β определять (рассчитывать) координаты ЦТ груза: x, y, z. Поскольку уравнений в системе два, а неизвестных координат - три, то необходимо провести, по меньшей мере два подвешивания (опыта), каждый из которых должен отличаться исходными данными, например, высотой первичного подвеса (h). При разной высоте h будут различными углы отклонения α, β. Таким образом, вместо системы двух уравнений мы получаем - четыре, чего вполне достаточно для решения задачи определения координат ЦТ груза. Например, пусть, в первом опыте высота первичного подвеса равна h1, при этом углы отклонения траверсы и груза - соответственно α1, β1. Во втором опыте - высота первичного подвеса h2, а углы отклонения - α2, β2. По результатам двух опытов можно составить следующую систему уравнений:

Решая совместно уравнения (9) и (11) можно получить формулу (1), а именно:
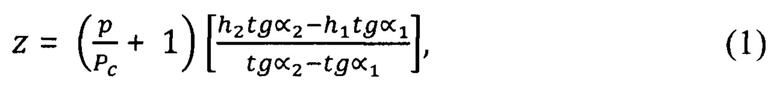
А решая совместно уравнения (10) и (12), соответственно получим формулу (2):

Решая совместно уравнения (9) и (11) и исключая из них переменную z, получим уравнение (3), а именно:

Аналогично, решая уравнения (10) и (12) относительно х, получим уравнение (4):

Таким образом, все три координаты центра тяжести груза определены. При этом высота расположения ЦТ относительно базы (погрузочной платформы) EFHJ может быть вычислена по двум разным формулам: (1) или (2). Это предоставляет нам дополнительные возможности по повышению точности получаемых результатов. Например, оба значения z, вычисленные по (1) и (2), можно сравнивать между собой. Если они окажутся равными, то это будет означать, что оба опыта (измерения) проведены качественно, без ошибок. Если же они окажутся разными, то необходимо установить причину этой разницы, и при необходимости, опыт может быть повторен (например, для еще одного значения высоты первичного подвеса h3 и т.д.). Полученные таким образом третье и четвертое значения z можно сравнить с остальными. Если есть уверенность в тщательности проведения первых двух опытов, то можно взять среднее значение высоты z, или то, которое позволяет сделать ошибку в безопасную сторону. Например, в случае определения высоты ЦТ груза, предназначенного к погрузке на судно подъемным устройством с применением многозвенной системы подвешивания, устойчивость которой должна быть проверена до начала грузовой операции, предпочтительным будет выбрать большее значение z.
И еще одно соображение по поводу выбора более подходящего значения z. Анализируя выражения (1, 2), можно увидеть, что уравнение (1) использует углы наклонения в одной плоскости (углы а - в плоскости ZOY), в то время как уравнение (2) - в другой (углы β в плоскости ZOX). Очевидно, в какой из плоскостей наклонение больше, а также разница наклонений между опытами больше - тем точнее результат вычисления z по соответствующей формуле. Например, углы наклонения (β1>α1 и β2>α2, кроме того разница между β1 и β2 так же значительна. Это означает, что при расчете высоты z следует отдать предпочтение формуле (2).
Пример реализации предложенного способа представлен на фиг. 1, 4-6. На фиг. 1 представлено положение системы подвешивания с грузом в исходном состоянии (перед первым опытом-подвешиванием). Крюк подъемного устройства 1 с помощью гибких первичных строп 2 равной длины l1=7 м соединяется с жесткой прямоугольной траверсой 3 массой 30 т (30000 кг) в точках ABCD. Размеры траверсы (между точками крепления) a=AB=ED=8 м; b=AE=BD=4 м. К этим же точкам ABCD траверсы 3 присоединяются гибкие вторичные стропы 4 равной длины 12 м (длина их может быть любой, и для проведения опыта-измерения это не имеет значения [5, 6]). Стропы 4 другими концами присоединяются к измеряемому объекту (грузу) 5 в точках EFJH (или его погрузочной платформе). Масса объекта 160 т (160000 кг).
Длину первичных строп 2  выбирают таковой, чтобы измеряемый объект 5 был полностью вписан в пирамиду первичного подвеса SABCD (фиг. 4). В этом случае устойчивость системы в процессе опыта (подвешивания) гарантирована.
выбирают таковой, чтобы измеряемый объект 5 был полностью вписан в пирамиду первичного подвеса SABCD (фиг. 4). В этом случае устойчивость системы в процессе опыта (подвешивания) гарантирована.
После того, как система будет полностью собрана и подготовлена к опыту с помощью крюка 1 ее поднимают и подвешивают (фиг. 4). В результате этого система деформируется: первичный подвес (стропы 2 и траверса 3) отклонится, так же отклонится и груз 5 на погрузочной платформе 6. При этом вторичные стропы 4 останутся в вертикальном положении (фиг. 4).
В подвешенном положении равновесия системы измеряют угол отклонения стороны траверсы АВ (CD) - α1=17,5°, а также угол отклонения стороны траверсы BD(AE) от исходного (горизонтального) положения -β1=8,9° (фиг. 5).
Замечание 3. Углы отклонения прямоугольника EFJH, образованного нижними точками крепления вторичных строп 4 будут такими же, поскольку траверса ABCD и база (погрузочная платформа) EFJH параллельны друг другу.
После измерения углов систему опускают в исходное положение и заменяют первичные стропы 2 на другие, имеющие другую (большую) длину  Система подвешивания с грузом и первичными стропами 2 длиной
Система подвешивания с грузом и первичными стропами 2 длиной  представлена на фиг. 5, 6. После этого систему вновь подвешивают и измеряют углы отклонения траверсы (или базы EFJH) α2=4,6° и β2=2,3°.
представлена на фиг. 5, 6. После этого систему вновь подвешивают и измеряют углы отклонения траверсы (или базы EFJH) α2=4,6° и β2=2,3°.
По известным размерам первичного подвеса вычисляют его высоту h1 (для первого опыта) и h2 (для второго) по формуле (6):

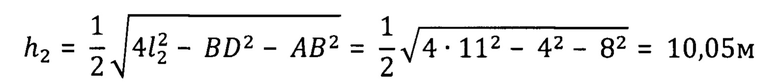
Далее по формуле (1) вычисляем координату z:

А по формуле (2) получим:

Полученные значения z, что свидетельствует о качественном проведении обоих опытов.
Теперь по формулам (4) и (3) вычислим координаты у и х соответственно:

Замечание 4. Пусть измеряемый объект 5 был установлен и жестко закреплен на погрузочной платформе 6, к которой и были прикреплены вторичные стропы 4 в точках EFJH. Предположим, что масса погрузочной платформы 6 равна рb=4 т (4000 кг), а координаты ее ЦТ: хb=уb=0, zb=0,3 м. Предположим также, что в проведенном выше примере (измерении) масса платформы входила в общую массу груза и платформы, то есть масса груза без платформы была равна:
Р=Рс - рb=156 т
В этом случае для получения координат ЦТ только груза (массой Р), полученные выше значения координат (обозначим их как: z1=4,50 м; х1=0,299 м; у1=0,030) необходимо пересчитать следующим образом:
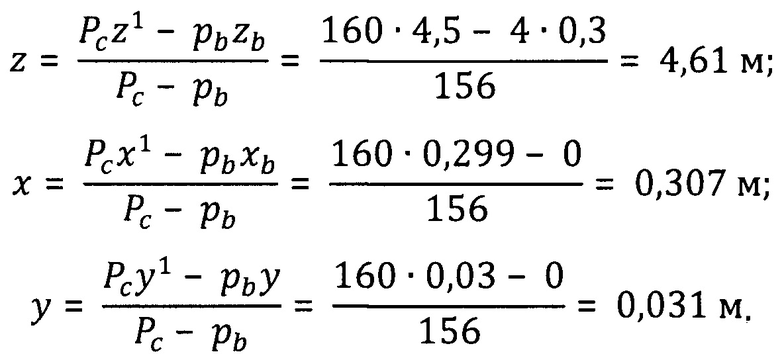
Литература
1. Умрихин В.И., Черный Н.В. Способ определения центра тяжести груза и устройство для его осуществления. Патент на изобретение: SU1 404431 А1. Опубликовано: 1988.06.23
2. Блинов И.А. Способ определения положения центра тяжести массивных изделий. Патент на изобретение RU 2721158 С1. 2020.05.18.
3. Kaps Н. (2009) ВВС Guideline. Safe Solutions for Project Cargo Operations. Version 1.0. BBC Chartering & Logistics GmbH&Ko. KG-68p.deckofficer.ru/titul/study/item/safe-solutions-for-project-cargo-operations
4. Kaps H. (2013) Stability of Cargo Suspension Arrangements. Transport Information Service (TIS) from the German Insurance Association, www.tis-gdv.de/tis_e/inhalt.html.
5. Никитин E.B., Устойчивость двухзвенной системы подвешивания груза с параллельными стропами вторичного подвеса. Вестник одесского национального морского университета. Сборник научных трудов. Вып.3 (39), 2013, с. 156-167.
6. Nikitin Yevgeny V. Static and tip-over stability analysis of two-chain suspension arrangements for large scale cargo operations//WMU Journal of Maritime Affairs. Volume 13, Number 1, April 2014, pp. 101-126. DOI 10.1007/s13437-013-0054-5.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения центра тяжести изделия подвешиванием по положению траверсы | 2021 |
|
RU2777341C1 |
| Способ определения положения центра тяжести массивных изделий | 2019 |
|
RU2721158C1 |
| СТРОПОВЫЙ ПОДВЕС | 2012 |
|
RU2520681C1 |
| Способ адаптивного управления мостовым краном | 2024 |
|
RU2830910C1 |
| СПОСОБ КАНТОВАНИЯ КРУПНОГАБАРИТНЫХ ЦИЛИНДРИЧЕСКИХ ГРУЗОВ | 2020 |
|
RU2742665C1 |
| ТРАВЕРСА | 2012 |
|
RU2526308C2 |
| ГРУЗОЗАХВАТНОЕ УСТРОЙСТВО ДЛЯ ТРАНСПОРТИРОВКИ КРУПНОГАБАРИТНОГО ЗЕРКАЛА ТЕЛЕСКОПА С ЦЕНТРАЛЬНЫМ ОТВЕРСТИЕМ | 2024 |
|
RU2837324C1 |
| ТРАВЕРСА ГОРИЗОНТАЛЬНОЙ СТЫКОВКИ, БЛОК ЗАДАНИЯ НАГРУЗКИ МЕХАНИЗМА БАЛАНСИРОВКИ ТРАВЕРСЫ, БЛОК КОМПЕНСАЦИИ ВЕКТОРА НАГРУЗКИ МЕХАНИЗМА БАЛАНСИРОВКИ ТРАВЕРСЫ, СПОСОБ НАСТРОЙКИ БАЛАНСИРОВКИ ТРАВЕРСЫ | 2008 |
|
RU2374164C1 |
| ГРУЗОЗАХВАТНОЕ УСТРОЙСТВО С КРЮКОМ-САМООТЦЕПОМ И САМООТКРЫВАЮЩИМСЯ ЗАТВОРОМ ПРИ СНЯТИИ ГРУЗА | 2003 |
|
RU2245291C2 |
| СПОСОБ УРАВНОВЕШИВАНИЯ ГРУЗОПОДЪЕМНОГО СТРЕЛОВОГО КРАНА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2281242C1 |





Изобретение относится к измерительной технике и может быть использовано для определения положения центра тяжести массивного и крупногабаритного объекта путем его подвешивания. Способ предполагает двукратное подвешивание объекта с помощью двухзвенной системы, у которой между подвешиваниями меняется длина первичных строп, измерение углов отклонения объекта и последующее вычисление координат его центра тяжести. Система подвешивания формируется таким образом, чтобы не допустить потерю устойчивости системы и возможное в таком случае опрокидывание и повреждение объекта. Технический результат заключается в обеспечении устойчивости системы подвешивания, недопущение опрокидывания и повреждения объекта, упрощение процедуры измерения и расчета положения его центра тяжести. 6 ил. 
Способ определения положения центра тяжести (ЦТ) массивных и крупногабаритных объектов сложной формы, заключающийся в присоединении объекта с помощью двух групп строп через промежуточную прямоугольную траверсу к крюку подъемного устройства, многократном поднятии и свободном подвешивании объекта до положения равновесия с разной пространственной ориентацией, измерении параметров ориентации объекта в подвешенном положении равновесия и последующем вычислении на их основе координат ЦТ груза, отличающийся тем, что первичные стропы, соединяющие траверсу и крюк подъемного устройства, выбирают одинаковой длины  и таковой, чтобы подвешиваемый измеряемый объект мог быть вписан внутрь пирамиды, образованной траверсой и этими стропами, вторичные стропы, соединяющие объект и траверсу, также выбирают равной длины и присоединяют к объекту и траверсе таким образом, чтобы они были вертикальны и параллельны друг другу, при каждом подвешивании и измерении разную пространственную ориентацию объекта в положении равновесия осуществляют путем изменения длины первичных строп
и таковой, чтобы подвешиваемый измеряемый объект мог быть вписан внутрь пирамиды, образованной траверсой и этими стропами, вторичные стропы, соединяющие объект и траверсу, также выбирают равной длины и присоединяют к объекту и траверсе таким образом, чтобы они были вертикальны и параллельны друг другу, при каждом подвешивании и измерении разную пространственную ориентацию объекта в положении равновесия осуществляют путем изменения длины первичных строп  , а саму эту ориентацию определяют с помощью измерения углов отклонения αi и βi от начального - горизонтального положения сторон прямоугольника, образованного точками крепления вторичных строп к объекту, после чего вычисляют вертикальную координату центра тяжести (z) объекта по одной из следующих формул:
, а саму эту ориентацию определяют с помощью измерения углов отклонения αi и βi от начального - горизонтального положения сторон прямоугольника, образованного точками крепления вторичных строп к объекту, после чего вычисляют вертикальную координату центра тяжести (z) объекта по одной из следующих формул:

или:

а затем вычисляют поперечную (х) и продольную (у) координаты центра тяжести объекта по формулам:


где Рс, р - масса объекта и траверсы, кг;
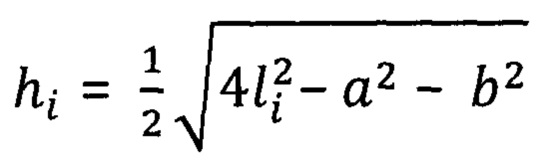 - высота пирамиды первичного подвеса при i-м подвешивании, м;
- высота пирамиды первичного подвеса при i-м подвешивании, м;
а, b - длина и ширина траверсы, м;
 - длина первичных строп при i-м подвешивании, м;
- длина первичных строп при i-м подвешивании, м;
αi, βi - углы отклонения объекта от горизонтали при i-м подвешивании, град.
| Способ определения положения центра тяжести массивных изделий | 2019 |
|
RU2721158C1 |
| Устройство для определения координат центра масс изделий | 1989 |
|
SU1677543A1 |
| Способ определения центра тяжести груза и устройство для его осуществления | 1986 |
|
SU1404431A1 |
| WO 2008122448 A1, 16.10.2008 | |||
| Kaps Н | |||
| Колосоуборка | 1923 |
|
SU2009A1 |
| Safe Solutions for Project Cargo Operations | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| BBC Chartering & Logistics GmbH&Ko | |||
| Способ получения смеси хлоргидратов опийных алкалоидов (пантопона) из опийных вытяжек с любым содержанием морфия | 1921 |
|
SU68A1 |
Авторы
Даты
2023-12-06—Публикация
2022-12-19—Подача