Изобретение относится к вычисли- телочой технике, а именно к специальным вычислительным устройствам функционального преобразования информации.
Цель изобретения - повышение быстродействия и достоверности вычислений.
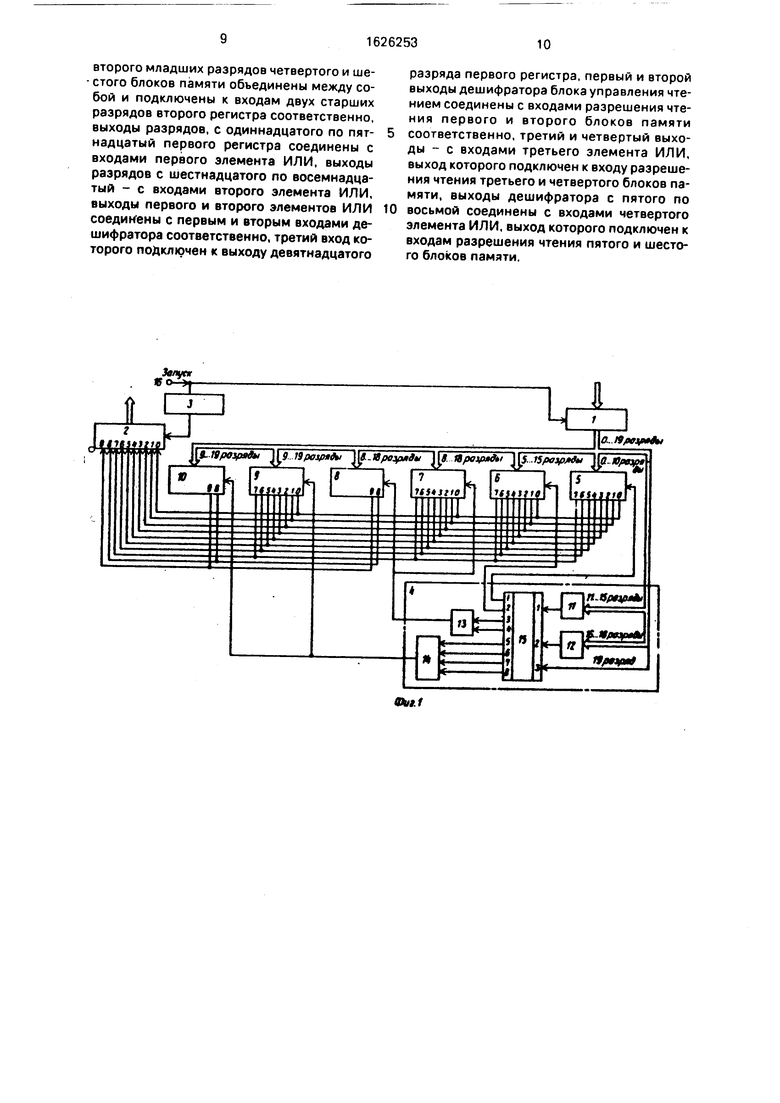
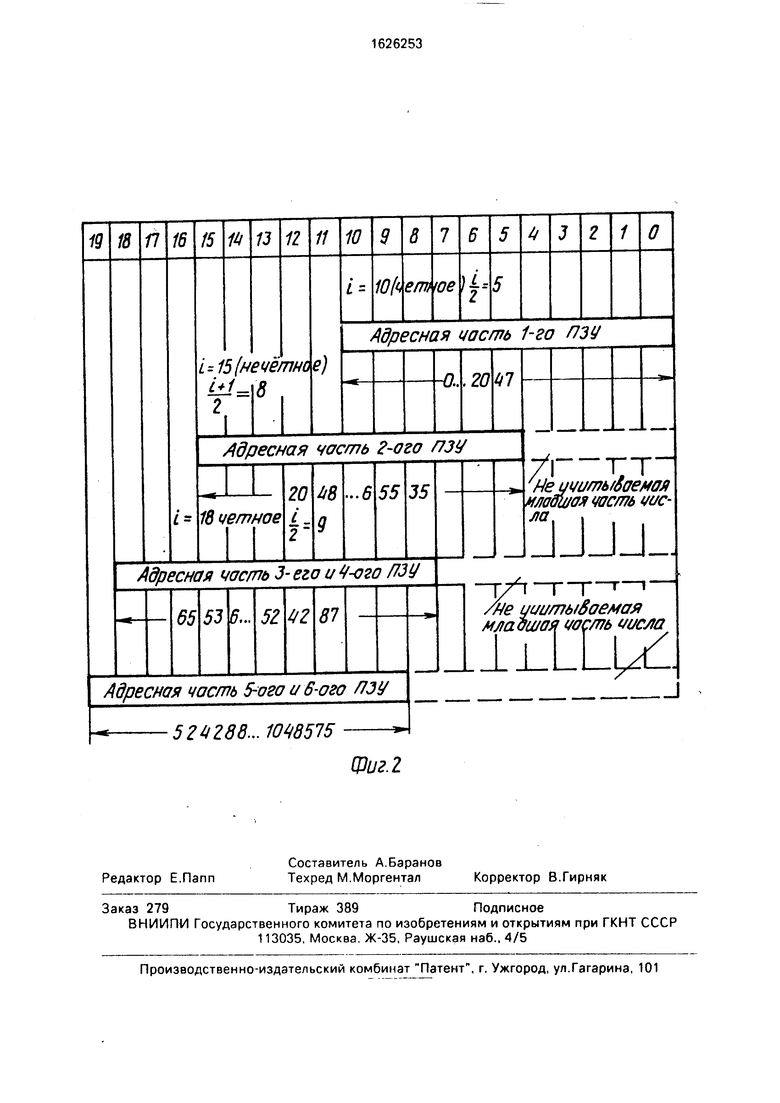
На фиг, 1 представлена структурная схема устройства; на фиг, 2 - формат числи, из которого производятся вычисления корня и распределение зон в этом формате для адресов каждого блока памяти.
Устройство содержит регистры 1 и 2, элемент 3 задержки, блок 4 управления чтением, блоки памяти (ПЗУ) 5-10 группы, блок 4 содержит элементы ИЛИ 11-14. дешифратор 15.
Сущность изобретения основана на ис- полизовании следующей закономерности:
12 1
22-(1 + 1)2 12 + 2х1 + 1 4
З2 - (2 + 1)2 22 + 2 х 2 + 1 9
42-(3+ 1)2 32 + 2хЗ + 1 t 16
52 (4 + 1)2 42 + 2 х 4 + 1 25 и т.д.
В общем виде (п+1)-й член данной последовательности можно представить как (п + 1 п2 + 2п + 1, если считать, что результат извлечения квадратного корня из целого числа есть целое число, то VА В и тогда А В2.
Если следовать в сторону увеличения числа А, то с определенного значения В + 1, при этом 6- 2В + 1, Таким образом, если задаться погрешностью 1, то для всех чисел от А по А + 2В значение квадратного корня будет В. H0VA-f2B + 1 -B+1.
Увеличение числа А на величину до (2В + 1) не вызывает изменения значения квадратного корня. Учитывая вышесказанное, можно написать следующую последовательность:
... 5 /25
6- /25 + 2 х 5 +1 /36 7 - 36Т2 х 6 +1 V49
Ё
О
ю
Os
го ел со
49+ 2x7+1
33 + 2 х 32 + 1 V1089 и т.д.
В последнем примере, если задаться погрешностью 1, значение квадратного корня 32 будет для всех чисел от 1024 до 1088, т.е. 65 значений.
Любое целое число А 1 в двоичной системе счисления можно представить в виде.
А а;Х2 + ам X 2м + амХ
+ ...+ aiX21+aoX2°, где ai 1, a(i-i)...a0 0,1. Это число находится в промежутке 21 А 2|+1. Значение квадратного корня из этого числа будет В - bi/2 X 2|/2 + bi/2 -1 X ... + bi X
X21 + bo X2°, 1, bi/2-i ... bo 0,1 если I - четное,
где bi/2 и
i + i
B b(i + ii/2 X2 гдеЬ(| + jj/2... bo
2 + ... + biX21 + boX2°, 0,1, если I - нечетное.
Если идти в сторону увеличения числа А, то следующее значение корня будет соответствовать В + 1, при этом число А увеличится на 2В + 1. Умножение на два числа в двоичной системе соответствует сдвигу влево числа на один разряд. Следовательно, если номер старшего разряда числа В был 1/2, то номер старшего разряда числа 2В
будет ( + 1). Таким образом, если VA В
и идти в сторону увеличения числа А, то значение корня В + 1 будет в том случае,
О|
если изменится (-н- + 1}-й разряд числа А,
при этом погрешность может быть 1. Изменения в разрядах младше указанного не вызывают изменения в значении квадратного корня. Следовательно, при извлечении квадратного корня из 1-разрядного числа можно не учитывать младшие разряды с 0-го по 1/2-й, Значащие разряды при этом будут
с (-j- + 1)-го по 1-й. Для уменьшения погрешности в два раза необходимо сократить в два раза не учитываемую часть числа, т.е. сдвинуты на один разряд вправо границу значащей частцчисла при извлечении квадратного корня. Если извлекать квадратный корень из .1-разрядного двоичного числа с погрешностью 0,5, можно не учитывать
младшие разряды с 0-го по (-у - 1}-й и только изменения в разрядах, начиная с l/2-го по 1-й влекут изменения в результате квадратного корня.
На фиг. 1 изображена блок-схема устройства для извлечения квадратного корня из всех чисел, ограниченных 20-ю двоичными разрядами. В качестве блоков памяти (ПЗУ) использована микросхема с организацией памяти 2К х 8. Блок памяти имеет 11
0 линий адреса с 0-го по 10-й разряды, N 10 и 8 линий данных, М 8, имеется также вход Разрешение чтения. При отсутствии сигнала на этом входе все 8 линий данных блока памяти находятся в третьем состоянии 5 состоянии высокого импеданса.
Блок 5 памяти программируется для всех чисел от 0 до 2047. Значение квадратного корня из 2047 соответствует 45. Если идти в сторону увеличения чисел, то следу0 ющее значение кормя будет 46, при этом подкоренное выражение увеличится по сравнению с предыдущим на 45 х 2 + 1 91, что соответствует с двоичной системе 1011011 (шесть разрядов, считая с нулево5 го). Таким образом, следующий блок памяти программируется не с 6-го разряда входного числа/ а с 5-го разряда и дальше до полного заполнения адресной части ПЗУ, т.е. по 15-й разряд. Программирование с 5-го раз0 ряда, а не с 6-го позволяет получить погрешность результата не более 0,5. ПЗУ 6 охватывает все числа от 2048 до 65535. Значение квадратного корня из 65535 соответствует 256 28. Следующее значение корня
5 257, при этом подкоренное значение увеличится на 256 х 2 + 1 513, т.е. изменение при этом произойдет в 9-м разряде. Следовательно, для получения погрешности не более 0,5 следующее ПЗУ 7 надо програм0 мировать не с 9-го разряда, а с 8-го разряда входного числа, и далее до полного заполнения адреса ПЗУ, т.е. по 18-й разряд числа от 65536 по 324287.
Корень квадратный из 324287 равен
5 724. Следующее значение 725 будет, если подкоренное значение увеличится на 724 х х 2 + 1 1449, т.е. изменение должно произойти в 10-м разряде, а для погрешности не более 0,5 следующее ПЗУ 9 программи0 руется с 9-го разряда входного числа и далее по 19-й разряд.
Выбранные ПЗУ имеют 8 линий данных. Поскольку в примере входное число может иметь все 20 разрядов значащих, т.е. логи5 ческие 1, то с некоторого значения результат извлечения квадратного корня может превысить 8 разрядов. Для этого в устройство введены еще два ПЗУ, ПЗУ 8 по адресной части подключено аналогично ПЗУ 7, а две линии данных предназначены для расширения разрядности результата извлечения корня (8-й и 9-й разряды). ПЗУ 10 работает совместно с ПЗУ 9, а две линии данных используются также для расширения разрядности результата.
Устройство работает следующим образом.
Двоичный код числа, из которого надо извлечь квадратный корень, поступает на информационные входы регистра 1. По сигналу Запуск, который поступает на управ- ляющий вход регистра 1, этот код записывается в регистр и поступает на адресную часть ПЗУ 5... ПЗУ 10 и блок 4 управления чтением. Причем разряды с 0-го по 10-й поступают на ПЗУ 5, разряды с 5-го по 15-й - на ПЗУ 6, разряды с 8-го по 18-й - на ПЗУ 7 и 8 и разряды с 9-го по 19-й - на ПЗУ 9 и 10.
Блок 4 управления чтением содержит входные элементы ИЛИ 11 и 12, дешифратор 15 и выходные элементы ИЛИ 14 и 13. Разряды с 11-го по 15-й с выхода регистра 1 через входной элемент ИЛИ 11 блока 4 управления чтением поступают на первый скод дешифратора 15. Разряды с 16-го по 18-й через входной элемент ИЛИ 12 блока 4 управления чтением поступают на второй вход дешифратора 15, а 19-й разряд - на третий вход дешифратора 15. Если в двоичном коде числа отсутствуют логические единицы в разрядах с 11-го по 19-й (фиг. 2), то на входах дешифратора 15 будет код ОООа (0) и на выходе 1 дешифратора 15 вырабатывается сигнал Разрешение чтения для ПЗУ 5, который активизирует выходы этого ПЗУ 5. Выходы остальных ПЗУ 6...ПЗУ 10 находятся в состоянии высокого импеданса. Значение квадратного корня, прошитое в этом ПЗУ 5, по данному адресу (код числа) с выходов ПЗУ 5 поступает на информационные входы регистра 2. Сигнал Запуск, задержанный элементом 3 задержки на время выборки ПЗУ, поступает на управляющий вход регистра 2 и двоичный код значения квадратного корня записывается в регистр 2.
Если в двоичном коде числа в разрядах с 11 -го по 15-й имеется хотя бы одна логическая 1, то эта логическая 1 через входной элемент ИЛИ 11 блока управления чтением поступает на первый вход дешифратора 15 и, при отсутствии логических единиц в разрядах с 16-го по 19-й, на входах дешифратора формируется код 001.
На выходе 2 дешифратора 15 вырабатывается сигнал Разрешение чтения для ПЗУ 6. который активизирует уже выходы этого ПЗУ 6. Выходы остальных ПЗУ 5, ПЗУ 7 ... ПЗУ 10 находятся в состоянии высокого
импеданса. Значение квадратного корня, прошитое в ПЗУ 6, по коду адреса с его выходов также поступает на информационные входы регистра 2. Если в двоичном коде
числа в разрядах с 16-го по 18-й присутствует хотя бы одна логическая 1. а в разряде 19 -логический О, то эта (эти) логическая 1 через входной элемент ИЛИ 12 блока управления чтением поступает на второй
0 вход дешифратора 15 и на входах дешифратора формируется код 010, если в разрядах с 11-го по 15гй не было логических 1, или 011, если в разрядах с 11-го по 15-й была хотя бы одна логическая 1. При этом либо
5 на выходе 3 дешифратора 15, либо на его выходе 4 вырабатываются сигналы Разрешение чтения, которые объединяются через выходной элемеш ИЛИ 13 и с выхода этого элемента сигнал Разрешение чтения
0 активизирует выходы ПЗУ 7 и ПЗУ 8. Использование двух ПЗУ в данном случае обусловлено тем, что разрядность значения квадратного корня из 19-разрядного числа может превысить количество линий данных
5 одного ПЗУ (в данном случае количество линий данных одного ПЗУ составляет 8). Поэтому ПЗУ 8 используется для наращивания данных до 10-ти разрядов; с 0-го по 7-й выходы с ПЗУ 7, а 8- и 9-й разряды - выходы
0 ПЗУ 8.
Если в 19-м разряде кода числа логическая 1, то на входе дешифратора 15 блока 4 управления чтением устанавливается код
100,если в разрядах с 11-го по 18-й нет ни 5 одной логической 1. При этом на выходе 5
дешифратора 15 вырабатывается сигнал Разрешение чтения. Если в 19-м разряде кода числа логическая 1 и в разрядах с 11-го по 18-й тоже могут быть логические 1, 0 то на входах дешифратора может быть код
101,сигнал Разрешение чтения при этом вырабатывается на 6-м выходе дешифратора 15, код 110 - на 7-м выходе и код 111 - на 8-м выходе дешифратора 15. Эти выходы
5 5-8 дешифратора 15 объединены выходным элементом ИЛИ 14 блока 4 управления чтением и с выхода элемента ИЛИ 14 сигнал Разрешение чтения активизирует выходы ПЗУ 9 и 10. Остальные ПЗУ 5 ... ПЗУ 8 нахо0 дятся в состоянии высокого импеданса. ПЗУ 10, в данном случае, используется аналогично ПЗУ 8 в предыдущем случае для расширения разрядности значения квадратного корня до 10-ти. Выходы с ПЗУ 9 - это разря5 ды с 0-го по 7-й; 8- и 9-й разряды - с ПЗУ 10. Для определения величины максимальной разрядности подкоренного выражения и количества ПЗУ в устройстве для извлечения квадратного корня необходимо задаться количеством линий адреса, выбранного
ПЗУ. В общем случае, если старший разряд адреса имеет номер N (0,1, ...N), то такое ПЗУ можно запрограммировать для всех 2 адресов, т.е. для всех чисеч от 0 до 2 запрограммировать значения их квадрат- ных корней.
Если разрядность чисел, из которых необходимо извлечь квадратный корень, превышает разрядность адресной части ПЗУ, то следующее, второе, ПЗУ программируется, начиная с N/2 разряда числа и далее по (N/2 + N) разряд, т.е. номер старшего разряда второго ПЗУ будегЗ Ч/2 разряда числа, из которого извлекается квадратный корень.
Следующее, третье ПЗУ будет программироваться, начиная с (3N/2):2 3N/4 разряда числа и старший разряд адреса будет соответствовать с 3N/4 + N 7N/4 разряда входного числа.
Следующее, четвертое ПЗУ программируется, начиная с 7N/4-.2 7N/8 разряда числа, а старший разряд адреса соответствует 7N/8 + N - 15N/8 разряда числа, и т.д.
Таким образом, номер старшего разря- да первого ПЗУ - N, второго - 3N/2, третьего - 7N/4. четвертого ISN/8-и т.д. В общем виде номера старших разрядов ПЗУ будут описываться выражением Nx2k-1 /2 - Nx(2-1/2k 1), где k- 1, 2, 3.... - количество ПЗУ. Предел этого выражения при k - °o характеризует максимальную разрядность подкоренного выражения, т.е.
Hm N(2-, )2N.(1)
k - оо
следовательно, с помощью ПЗУ можно запрограммировать фунцию квадратного корня для всех чисел, разрядность которых в двоичном коде в два раза превышает разрядность адресной части ПЗУ.
Для определения количества ПЗУ, для реализации выражения (1) необходимо решить уравнение
N(2-1/2k-1) 2N-1;
2N-N2/2IM -2N-1;
N/2k 1-1;
2k 1 - N;
k-1 loga N;
k - 1 + loga N(2)
Поскольку количество ПЗУ может быть только целым числом, то при вычислении k по выражению (2) результат надо округлить в большую сторону до целого числа, т.е.
k 1 + Iog2 N.(3) Выражение (3) показывает необходи- мое количество ПЗУ с адресной частью в (N + 1) разрядов (от 0 до N) для реализации функции квадратного корня с погрешностью 0,5 для всех возможных для данного
случая чисел. Выражение (3) не учитывает тот факт, когда рязрядность значения квадратного корня может превысить разрядность линий данных ПЗУ. Этот случай зависит от организации памяти ПЗУ.
В примере, описанном выше, выбрано ПЗУ с организацией памяти 2К х 8, N 10. С помощью такого ПЗУ можно реализовать функцию квадратного корня для всех чисел с разрядностью до 2N 20, при этом количество ПЗУ будет k 1 + IOQ2 10 5 без учета расширения линий данных. Повышение быстродействия в предлагаемом устройстве достигается за счет применения ПЗУ запрограммированных как функция квадратного корня от значения адреса Д V| AI . Таким образом, время вычислений здесь совпадает с временем выборки ПЗУ и для массовых ПЗУ составляет 100...500 не.
Повышение достоверности обусловлено тем, что в схеме устройства отсутствуют всякого рода счетчики, триггеры и другие элементы, требующие специальных мероприятий по помехозащищенности. Число, из которого извлекается квадратный корень, является непосредственным адресом ПЗУ, в котором запрограммирован результат.
Формула изобретения Устройство для извлечения квадратного корня, содержащее первый и второй регистры, управляющий вход последнего из которых подключен к выходу элемента задержки, отличающееся тем, что, с целью повышения быстродействия и достоверности вычислений, в него введена группа из шести блоков памяти и блок управления чтением, содержащий дешифратор и четыре элемента И ПИ, причем вход запуска устройства подключен к входу элемента задержки и управляющему входу первого регистра, информационный вход которого соединен с информационным входом устройства, а выходы разрядов с нулевого по десятый - с соответствующими адресными входами первого блока памяти, выходы разрядов с пятого по пятнадцатый первого регистра соединены с адресными входами второго блока памяти, выходы разрядов с восьмого по восемнадцатый - с соответствующими адресными входами третьего и четвертого блоков памяти, а выходы разрядов с девятого по девятнадцатый - с соответствующими адресными входами пятого и шестого блоков памяти, разрядные выходы первого, второго, третьего и пятого блоков памяти объединены между собой и подключены к соответствующим разрядным входам второго регистра, выходы первого и
второго младших разрядов четвертого и шестого блоков памяти объединены между собой и подключены к входам двух старших разрядов второго регистра соответственно, выходы разрядов, с одиннадцатого по пятнадцатый первого регистра соединены с входами первого элемента ИЛИ, выходы разрядов с шестнадцатого по восемнадцатый - с входами второго элемента ИЛИ, выходы первого и второго элементов ИЛИ соединены с первым и вторым входами дешифратора соответственно, третий вход которого подключен к выходу девятнадцатого
разряда первого регистра, первый и второй выходы дешифратора блока управления чтением соединены с входами разрешения чтения первого и второго блоков памяти соответственно, третий и четвертый выходы - с входами третьего элемента ИЛИ, выход которого подключен к входу разрешения чтения третьего и четвертого блоков памяти, выходы дешифратора с пятого по восьмой соединены с входами четвертого элемента ИЛИ, выход которого подключен к входам разрешения чтения пятого и шестого блоков памяти.



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для формирования дуг и окружностей на экране телевизионного индикатора | 1990 |
|
SU1800476A1 |
| Вычислительная система | 1989 |
|
SU1734101A1 |
| УСТРОЙСТВО ПОИСКА ИНФОРМАЦИИ | 2006 |
|
RU2313128C1 |
| Устройство для сортировки @ -ичных чисел (его варианты) | 1984 |
|
SU1265758A1 |
| Устройство для отсчета времени | 1990 |
|
SU1784959A1 |
| Устройство для контроля хода программ | 1988 |
|
SU1545223A1 |
| Оперативное запоминающее устройство | 1990 |
|
SU1751812A1 |
| Устройство кодирования-декодирования числовых последовательностей | 1990 |
|
SU1809541A1 |
| Многоканальное устройство тестового контроля логических узлов | 1990 |
|
SU1837295A1 |
| Устройство для обработки нечеткой информации | 1989 |
|
SU1674145A1 |
Изобретение относится к вычислительной технике и может быть использовано дня вычисления квадратного корня в функциональных преобразованиях информации. Цель изобретения - повышение быстродействия и достоверности вычисления квадрат- ного корня. Цель достигается введением группы ПЗУ и блока управления чтением с соответствующими связями Это позволяет сделать число, из которого извлекается кчлдратный корень, непосредственным ад- р гом ПЗУ, в котором запрограммирован результат, чтп приводит к повышению быстродействия и экономии оборудования. 2 ил.


| Авторское свидетельство СССР N | |||
| Устройство для извлечения квадратного корня | 1980 |
|
SU949654A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Авторское свидетельство СССР Г 1146652, кл G 06 7/552 | |||
| Гребенчатая передача | 1916 |
|
SU1983A1 |
Авторы
Даты
1991-02-07—Публикация
1989-04-05—Подача