Известны арифметические устройства цифровых моделей, содержащие множительно-суммирующее устройство, счетчики и регистры.
Предлагаемое устройство отличается тем, что в нем к выходам регистра результата множительного устройства с частичным суммированием частных произведений подключена схема сравнения предсказанных и уточненных значений приращений, выходы которой соединены с реверсивным счетчиком порядка формул интегрирования, его выходы подсоединены к схеме управления считывания из долговременного запоминающего устройства констант, к регистру управления выборкой приращений подынтегральной функции и к устройству управления моделью.
Это позволяет повысить эффективность использования устройства.
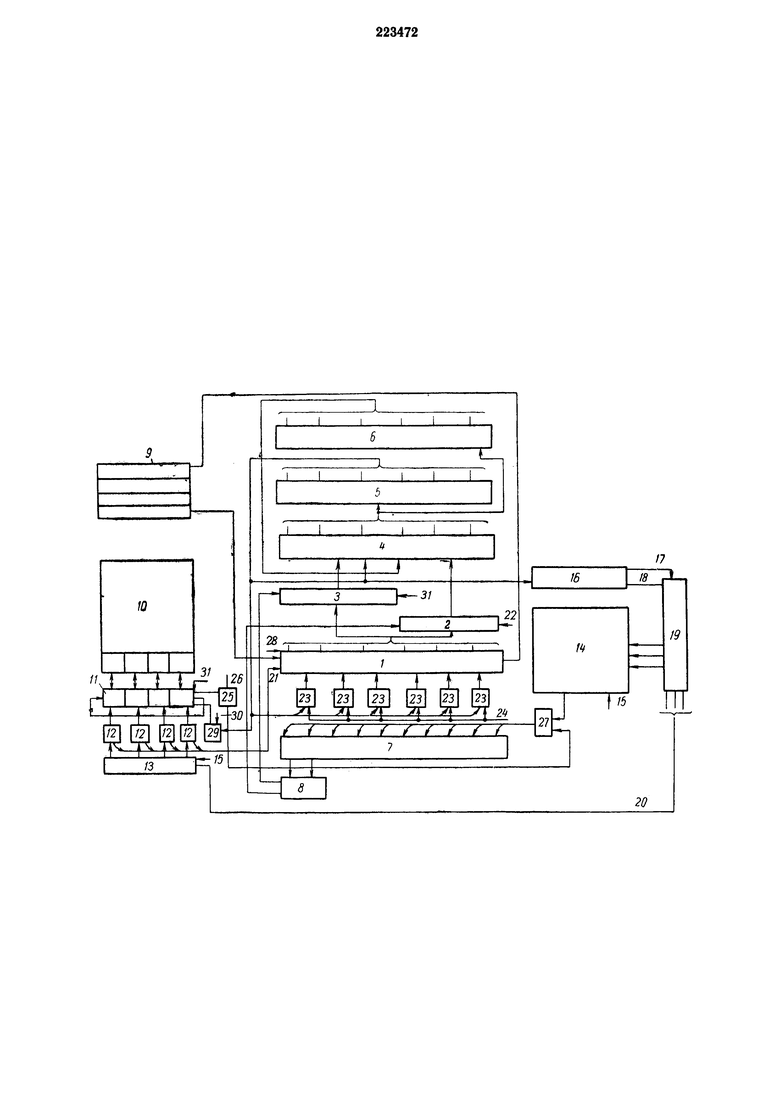
Блок-схема предлагаемого устройства представлена на чертеже, на котором приняты следующие обозначения: регистр 1 множимого, вентили 2 прямой передачи числа, вентили 3 инверсионной передачи числа, комбинационные сумматоры 4, регистр 5 суммы, регистр 6 переносов, регистр 7 множителя, схема 8 анализа двух старших разрядов множителя, магнитное оперативное запоминающее устройство (МОЗУ) 9 для хранения значений подынтегральной функции, магнитное оперативное запоминающее устройство 10 для хранения значений полноразрядных приращении, регистр 11 сдвига, клапаны 12, регистр 13 сдвига с управляемыми цепями обратной связи, долговременное запоминающее устройство (ДЗУ 14, шина 15 блока управления машины (последняя не показана на чертеже), блок 16 сравнения, шина 17 перехода к формулам более высокого порядка, шина 18 перехода к формулам интегрирования на порядок ниже, реверсивный счетчик 19 с группой шин 20, шина 21 передачи приращений, шина 22 управления клапанами, вентили 23, шина 24 управления вентилями, клапаны 25, шина 26 управления, схема 27 «ИЛИ», цепь 28 передачи одиночного импульса сдвига, группа вентилей 29, шина 30 управления, шина 31 управления вентилями инверсной передачи.
Формулы численного интегрирования, включая формулы 3-го порядка (порядок интерполяционной формулы может быть выбран на порядок ниже, чем для экстраполяционной формулы), сведены в табл. 1.
Символ ~ означает уточненные значения подынтегральной функции и интеграла.
Экстраполяционная формула (предиктор) используется для получения приближенного значения Yn+1, которое далее используется для получения величины 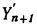 , затем значение Yn+1 уточняется по интерполяционной
, затем значение Yn+1 уточняется по интерполяционной

формуле (корректор), и полученная величина используется в дальнейших вычислениях. Величина 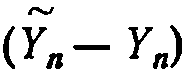 является мерой точности решения.
является мерой точности решения.
Так как обычно оперируют с разностными представлениями, нас интересуют формулы, выражающие ΔYn=Yn+1-Yn явно через подынтегральную функцию. Такие формулы могут быть получены путем замены ΔYn-1, ΔYn-2, ΔYn-3 на 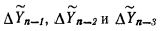 и т.д., полученных из интерполяционных формул того же порядка, что и экстраполяционные формулы (см. табл. 1). Соответствующие формулы сведены в табл. 2. При этом учитываются соотношения:
и т.д., полученных из интерполяционных формул того же порядка, что и экстраполяционные формулы (см. табл. 1). Соответствующие формулы сведены в табл. 2. При этом учитываются соотношения:
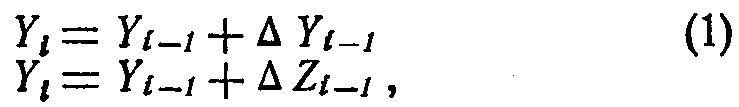
где: 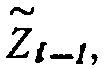 приращение, полученное на выходе другого интегратора.
приращение, полученное на выходе другого интегратора.
Как это следует из табл. 2, с увеличением порядка формул предикатора резко возрастает как сложность формул, так и количество хранимых величин. В случае формул порядка 0,1 необходимо хранить величины ΔYn, 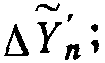 в случае формул порядка 2 необходимо хранить
в случае формул порядка 2 необходимо хранить 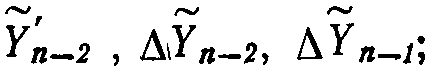 в случае формул порядка 3 необходимо хранить
в случае формул порядка 3 необходимо хранить 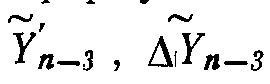
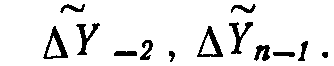
Анализ формул, представленных в табл. 2, показывает, что арифметические устройство должно содержать суммирующее и множительное устройства, связанные с ДЗУ констант и с местным устройством управления. Блок управления должен получать сигналы от устройства сравнения, в котором производится

сравнение величин ΔYn и 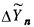 . Итерация разбита на два цикла: цикл вычисления ΔYn на основе формул предикторов и цикл вычисления
. Итерация разбита на два цикла: цикл вычисления ΔYn на основе формул предикторов и цикл вычисления 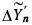 на основе формул корректоров. После вычисления скорректированного значения ΔYn заменяется на
на основе формул корректоров. После вычисления скорректированного значения ΔYn заменяется на 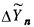 в ЗУ. Производится сравнение ΔYn с
в ЗУ. Производится сравнение ΔYn с 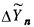 и, если
и, если 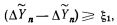 то местный блок управления реализует квадратурные формулы большего на единицу порядка. Блок управления также должен осуществлять обратное переключение к формулам на порядок ниже. Подобное переключение должно осуществляться каждый раз, когда
то местный блок управления реализует квадратурные формулы большего на единицу порядка. Блок управления также должен осуществлять обратное переключение к формулам на порядок ниже. Подобное переключение должно осуществляться каждый раз, когда 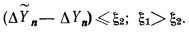
Арифметическое устройство содержит множительное устройство с промежуточным суммированием частных произведений, включающее регистр 1 множимого, вентили 2 прямой передачи числа, вентили 3 инверсной передачи числа, вентили 3 инверсной передачи числа, комбинационные сумматоры 4 на три входа, регистр 5 суммы, регистр 6 переносов, регистр 7 множителя и схему 8 анализа двух старших разрядов. Указанное множительное устройство общеизвестно и не является объектом изобретения. Разрядная сетка для величин 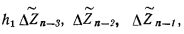 ΔZn может быть выбрана меньшей, чем разрядная сетка для величины
ΔZn может быть выбрана меньшей, чем разрядная сетка для величины 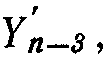 поэтому может быть получена некоторая экономия объема ЗУ в том случае, если в ЗУ хранятся значения
поэтому может быть получена некоторая экономия объема ЗУ в том случае, если в ЗУ хранятся значения 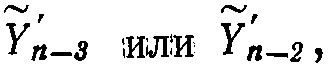 или
или 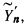 а также набор величин
а также набор величин 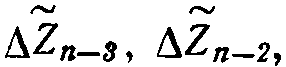
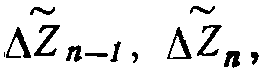 что позволяет в случае необходимости по формулам 1 перейти к требуемым значениям Y. Величины Y хранятся в МОЗУ 9, при этом осуществляется жесткий опрос МОЗУ, адрес увеличивается на единицу за каждую итерацию. В этом отношении организация адресной системы МОЗУ 9 не отличается от организации МОЗУ хранения подынтегральной функции цифрового дифференциального анализатора (ЦДА) и также не является объектом изобретения.
что позволяет в случае необходимости по формулам 1 перейти к требуемым значениям Y. Величины Y хранятся в МОЗУ 9, при этом осуществляется жесткий опрос МОЗУ, адрес увеличивается на единицу за каждую итерацию. В этом отношении организация адресной системы МОЗУ 9 не отличается от организации МОЗУ хранения подынтегральной функции цифрового дифференциального анализатора (ЦДА) и также не является объектом изобретения.
В МОЗУ 10 параллельно хранятся значения 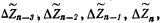 составляющие одну числовую линейку. Адресная система выборки линейки приращений
составляющие одну числовую линейку. Адресная система выборки линейки приращений 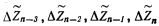 аналогична системе выборки приращений для ЦДА. При этом могут быть применены любые блоки с мнемонической организацией выборки соответствующих приращений. Так как эта часть предполагается известной, она не отражена на чертеже.
аналогична системе выборки приращений для ЦДА. При этом могут быть применены любые блоки с мнемонической организацией выборки соответствующих приращений. Так как эта часть предполагается известной, она не отражена на чертеже.
Считанный набор приращений 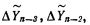
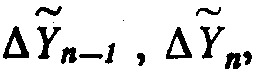 хранится в регистре 11 сдвига. Считывание данных из регистра 11 производится клапанами 12, управляемыми регистром 13 сдвига с управляемыми цепями обратной связи. Регистр 13 также управляет считыванием соответствующих констант из ДЗУ 14 в зависимости от цикла итерации. Информация о том, является ли он циклом вычисления по формулам предиктора или по формулам корректора, поступает по шине 15. Регистр 13 также получает информацию от блока 16 сравнения, на выходе которого на шине 17 вырабатывается сигнал перехода к формулам интегрирования на порядок выше, если
хранится в регистре 11 сдвига. Считывание данных из регистра 11 производится клапанами 12, управляемыми регистром 13 сдвига с управляемыми цепями обратной связи. Регистр 13 также управляет считыванием соответствующих констант из ДЗУ 14 в зависимости от цикла итерации. Информация о том, является ли он циклом вычисления по формулам предиктора или по формулам корректора, поступает по шине 15. Регистр 13 также получает информацию от блока 16 сравнения, на выходе которого на шине 17 вырабатывается сигнал перехода к формулам интегрирования на порядок выше, если 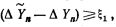 и вырабатывается сигнал на шине 18 перехода к формулам интегрирования на порядок ниже, если
и вырабатывается сигнал на шине 18 перехода к формулам интегрирования на порядок ниже, если 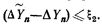 Эта информация поступает на реверсивный счетчик 19 порядка формулы интегрирования, который непосредственно связан с регистром 13 при помощи группы шин 20, а также с ДЗУ 14. В зависимости от состояния счетчика 19 регистр 13 осуществляет выборку соответствующей последовательности приращений, которые по группе шин 21 поступают в регистр 1. Одновременно из ДЗУ 14 через схему 27 «ИЛИ» передаются соответствующие константы, а из блока управления, на который поступает группа сигналов по шине 20, подаются управляющие сигналы. Множительное устройство при этом умножает приращения на соответствующие константы под воздействием сигналов управления из блока управления. Цепи организации сдвига на чертеже не показаны.
Эта информация поступает на реверсивный счетчик 19 порядка формулы интегрирования, который непосредственно связан с регистром 13 при помощи группы шин 20, а также с ДЗУ 14. В зависимости от состояния счетчика 19 регистр 13 осуществляет выборку соответствующей последовательности приращений, которые по группе шин 21 поступают в регистр 1. Одновременно из ДЗУ 14 через схему 27 «ИЛИ» передаются соответствующие константы, а из блока управления, на который поступает группа сигналов по шине 20, подаются управляющие сигналы. Множительное устройство при этом умножает приращения на соответствующие константы под воздействием сигналов управления из блока управления. Цепи организации сдвига на чертеже не показаны.
В регистре 5 образуется сумма произведений приращений на соответствующие константы.
Затем по сигналам блока управления осуществляется выборка 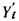 . В том случае, если не поступают сигналы по шинам 17 или 18, то в МОЗУ 9 в выбираемой ячейке хранятся соответствующие формулам заданного порядка (табл. 2) значения величины
. В том случае, если не поступают сигналы по шинам 17 или 18, то в МОЗУ 9 в выбираемой ячейке хранятся соответствующие формулам заданного порядка (табл. 2) значения величины 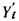 .
.
При изменении порядка на блок управления передаются сигналы об изменении порядка, при этом нормальная последовательность действий нарушается, и по формулам 1 осуществляется переход к требуемому значению 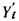 .
.
В нормальном (установившемся) режиме 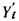 записывается в регистр 1 и через вентиль 2, управляемый сигналом по шине 22, поступает на накопительный регистр 5. Далее содержимое регистра 5 переписывается в регистр 1 через группу вентилей 23, открываемых сигналом по шинам 24, поступающим из блока управления. Одновременно из МОЗУ 10 выбирается соответствующее значение ΔУn или h, которое через клапаны 25, управляемые сигналом по шинам 26 от блока управления, и схему «ИЛИ» 27 переписывается в регистр множимого 1.
записывается в регистр 1 и через вентиль 2, управляемый сигналом по шине 22, поступает на накопительный регистр 5. Далее содержимое регистра 5 переписывается в регистр 1 через группу вентилей 23, открываемых сигналом по шинам 24, поступающим из блока управления. Одновременно из МОЗУ 10 выбирается соответствующее значение ΔУn или h, которое через клапаны 25, управляемые сигналом по шинам 26 от блока управления, и схему «ИЛИ» 27 переписывается в регистр множимого 1.
Необходимо отметить, что в случае формул нулевого, первого и второго порядка запись 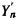 производится таким образом, что по отношению к взвешенной сумме приращений записывается число
производится таким образом, что по отношению к взвешенной сумме приращений записывается число 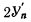 , однако, до суммирования по цепи 28 поступает один импульс сдвига. В случае формул третьего порядка указанный импульс не поступает.
, однако, до суммирования по цепи 28 поступает один импульс сдвига. В случае формул третьего порядка указанный импульс не поступает.
Далее осуществляется цикл умножения на h или 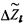 . При этом случае формул третьего порядка из МОЗУ 10 выбирается приращение
. При этом случае формул третьего порядка из МОЗУ 10 выбирается приращение 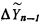 . Цикл переписи
. Цикл переписи 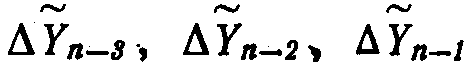 и ΔYn на регистр 11 производится для формул любого порядка.
и ΔYn на регистр 11 производится для формул любого порядка.
Приращение ΔYn-1 вычитается из величины, хранимой в регистре 5. Затем содержимое регистра 5 переписывается через группу вентилей 29, управляемых сигналом по шине 30 блока управления, в ячейку регистра 11. Предварительно в регистре 11 производится сдвиг информации на одну ячейку влево.
Второй цикл вычислений по формулам предиктора осуществляется аналогичным образом.
Отличия второго цикла заключаются в численных значениях констант, а также в последовательности выборки сигналов 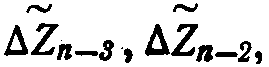
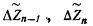 . Сигналы от блока управления переключают регистр 13 и схему ДЗУ 14. В конце цикла импульс сдвига по шине 31 не подается, поэтому Yn заменяет ранее записанное значение Yn.
. Сигналы от блока управления переключают регистр 13 и схему ДЗУ 14. В конце цикла импульс сдвига по шине 31 не подается, поэтому Yn заменяет ранее записанное значение Yn.
Необходимо отметить, что значение Yn переписывается через группу вентилей 23 и поступает на регистр 1. Устройство управления открывает группу вентилей 3 путем подачи сигнала по шине 31, в результате чего в регистре 5 образуется 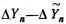 . Величина
. Величина 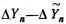 переписывается в блок 16, в котором образуется
переписывается в блок 16, в котором образуется 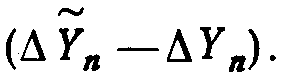 Соответствующие дешифраторы формируют сигналы по шинам 17 и 18; которые управляют работой схемы, в течение двух следующих циклов.
Соответствующие дешифраторы формируют сигналы по шинам 17 и 18; которые управляют работой схемы, в течение двух следующих циклов.
В данном случае рассматривалось устройство, реализующее формулы 0-3 порядков. Очевидно, что тот же самый принцип может быть распространен и на формулы более высокого порядка.
В устройстве реализован асинхронный принцип работы, вычисление по формулам более низкого порядка производится хотя и с тем же шагом, что и по формулам более высокого порядка, однако, в блоке управления генерируется сигнал о том, что суммирующее и множительное устройства свободны. Цифровая модель также снабжена МОЗУ универсальной части ЦВМ, не показанным на чертеже.
Соответствующие вычисления производятся в арифметическом устройстве в те моменты времени, когда производятся вычисления по формулам более низкого порядка. Это позволяет повысить эффективность использования арифметического устройства цифровой модели, а также увеличить его быстродействие.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОМБИНИРОВАННАЯ ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА | 1966 |
|
SU224910A1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО СПЕЦИАЛИЗИРОВАННОЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ | 1969 |
|
SU234753A1 |
| Цифровой интегратор для однородных цифровых интегрирующих структур (оцис) с плавающей запятой | 1973 |
|
SU510727A1 |
| Интегроарифметическое устройство | 1990 |
|
SU1784975A1 |
| Стереоавтограф | 1960 |
|
SU147841A1 |
| Цифровой интегратор с плавающей запятой | 1975 |
|
SU590774A2 |
| СТАТИСТИЧЕСКИЙ АНАЛИЗАТОР | 1969 |
|
SU255658A1 |
| Многофункциональное запоминающее устройство | 1972 |
|
SU458037A1 |
| РЕШАЮЩИЙ БЛОК ДЛЯ ЦИФРОВОГО ДИФФЕРЕНЦИАЛЬНОГО | 1972 |
|
SU355631A1 |
| ЦИФРОВОЙ ИНТЕГРАТОР | 1973 |
|
SU369590A1 |
Арифметическое устройство цифровой модели, содержащее множительно-суммирующее устройство, счетчики и регистры, отличающееся тем, что, с целью повышения эффективности его использования, в нем к выходам регистра результата множительного устройства с частичным суммированием частных произведений подключена схема сравнения предсказанных и уточненных значений приращений, выходы которой соединены с реверсивным счетчиком порядка формул интегрирования, его выходы подсоединены к схеме управления считывания из долговременного запоминающего устройства констант, к регистру управления выборкой приращений подынтегральной функции и к устройству управления моделью.
Авторы
Даты
1968-11-13—Публикация
1967-05-27—Подача