Попытки механического решения математических уравнений, особенно уравнений высших степеней, насчитывают не один десяток лет. Они повели к изобретению довольно сложных по устройству и в работе специальных машин для решения уравнений. Однако в широкий обиход прикладной математики-математики технических расчетов, вычисления физических постоянных и статистических выкладок ни одна из машин этого рода до сих пор не вошла. Расчетчики-вычислители, работающие в разнообразных областях точного и научно-технического знания и до сих пор вынуждены затрачивать на нахождение с необходимой точностью корней уравнений высших степеней довольно много труда и времени. С точки зрения практики в этой работе ценным является только результат работы-вычисленные корни уравнения, а не процесс работы, не процесс вычисления корней.
Эти обстоятельства настойчиво требуют механизации процесса вычисления корней уравнений высших степеней.
Предлагаемая машина для решения уравнений дает возможность выделять и вычислять корни уравнений высших степеней с одним неизвестным с точностью до единиц третьей значущей цифры, что в большинстве случаев решения уравнений может вполне удовлетворить требованиям практики.
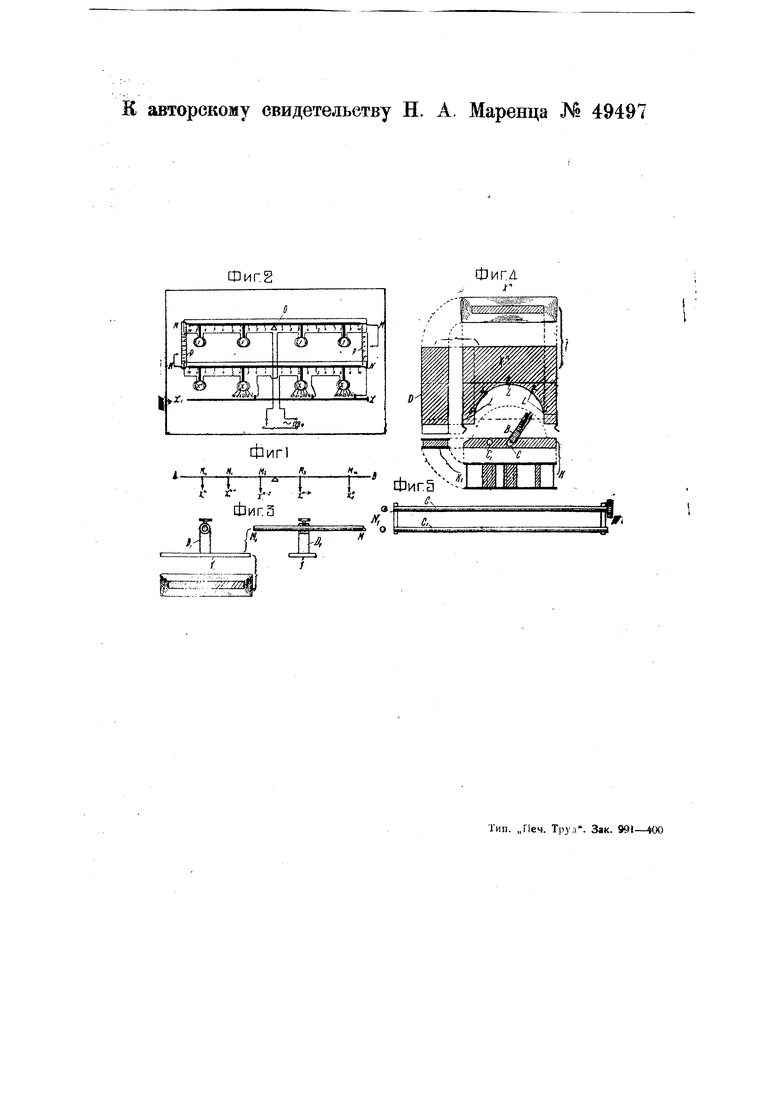
Предлагаемая машина основана на механической интерпретации целого рационального многочлена с действительными коэфициентами /(X) А,х + А,х- + А, - . . . , заключающейся в следующем. Если на оси АОВ (фиг. 1), которая может вращаться около точки О, отрезки ОМ, OAfj, OyW., OMs, .... ОМ„ численно равны коэфициентам многочлена f(x) и в точках MO . Wa, MS - . . М приложены перпендикулярно к оси и одинаково направленные силы соответственно пропорциональные числам Х Х . . .Х„ Хо„ то сумма всех вращающих моментов будет численно равна значению многочлена f{x).
Если, меняя силу Xi, мы найдем такое ее значение X., которое приведет систему АОВ в состояние покоя, то, очевидно, сумма всех вращающих моментов при этом будет равна нулевому значению многочлена f(x), т. е. будетДЛ,) 0 и, следовательно X. будет корнем этого многочлена.
Таким образом, вычисление корней уравнения/(л:) О может быть сведено к непосредственному измерению силы Хs момент, когда система ЛОВ приходит в состояние статического равновесия.
Принцип устройства предлагаемой I машины для решения уравнений легко усмотреть из прилагаемого чертежа (фиг, 2).
На чертеже фиг. 2 изображает схему общего расположения частей предлагаемой машины и схему ее электрических соединений. На близком расстоянии располагаются две параллельных между собой металлических, одинаково градуированных рейки ММ и .VA/,, причем первая из них ММ устроена поворотной в горизонтальной (или в вертикальной плоскости вокруг точки О (фиг. 2), а вторая NNi-неподвижной в этом случае на ММ применяются уравновешиваюш,ие передвижные грузики).
Рейка MMi снабжена передвижными по ней соленоидами 7, /, 7 и т. д., имеющими одинаковое число витков, принятое за единицу, а рейка Л/Л, снабжена также передвижными по ней соленоидами Х, Х, Х , Х и т. д., причем соленоид имеет число витков, равное числу витков на соленоидах /, а соле- ноиды Х, Х-, Л - и т. д. состоят каждый из десяти (или, например, из пяти; тогда для решения уравнения, имеющего границу корней выше 5, надо его преобразовать подстановкой х 2у) секций, первая из которых для всех этих соленоидов имеет одинаковое число витков, равное числу витков, имеющихся на каждом из соленоидов 7, 7, 7 и т. д.; каждая же из последующих секций заключает в себе все предыдущие секции соленоида, причем количества витков в секциях соленоида X относятся, как 1:2:3...., в Секциях соленоида Х, как ..., в секциях соленоида X, как 1 ..., в секциях соленоида X, как 1 : 2 : 3 и т. д.
Соленоиды крепятся на рейках посредством держателей D, дающих возможность быстро устанавливать в любом месте рейки любой соленоид (фиг. 3 и 4), причем держатели каждого из соленоидов X, Х, Х и т. д. снабжены дугой (фиг. 4), несущей контактные пластинки / от секций соленоидов и дающей возможность быстро передвигать соленоиды месте с контактными пластинками В, кользящими вдоль граненых осей С и Q.
Поворачивая ось С, можно включать посредством контактных пластинок А и S то или иное число секций, причем пластинки размещаются по дуге так, чтобы контактные пластинки В могли включать одновременно секции только с одинаковыми номерами, начиная от первой, как показано это схематически на фиг. 2.
Все соленоиды соединяются последовательно и замыкаются через реостат на городскую сеть, вследствие чего во всех соленоидах появляется одинаковая сила тока. Переключательными контактными ппастинками В (или, как показано схематически на фиг. 1, переключателем LL) можно включать в соленоидах X, Х, Х и т. д. секции витков с одним и тем же номером, который и укажет корень уравнения, если предварительно были расставлены соленоиды А , X, Х и т. д. на расстояниях от точки О, пропорциональных коэфициентам членов уравнения с ответственными степенями неизвестного, и если также расставлены на рейке ММ соленоиды 7, 7, 7 и т. д.
Если, например, после включения переключателем LL трех секций соленоидов X, Х, и т. д. сумма вращающих рейку MMi моментов станет равной
нулю, то будем иметь Ло К 3 -}-A,, ..., где Л - коэфициент пропорциональности, зависящий главным образом от силы тока (соленоиды включаются в городскую сеть напряжения 120 вольт через особое коммутаторное устройство) и числа витков в соленоидах , 7, 7, 7 ... После сокращения на будем иметь:
Аг,П tяпП1 ял(2 I
о 3 -f л 3 -|- - 4-|- Л, о и, следовательно, число 3 будет корнем данного уравнения.
Для более плавного вращения рейки АГ/И концы реек MMi и MVj можно соединить слабой пружинкой Р со шкалой, показывающей приближение к корню и дающей возможность приближенно оценить следующий (например после найденного знака 3) знак корня.
Если же между каждой паров основных выводов секций сделать еще по девяти промежуточных, то второй знак корня можно будет отсчитывать с по мощью переключателя так же, как и первый; при этом по шкале пружины Р
можно будет оценить приблизительно третий знак корня. Найдя же три знака корня и применив один раз способ Ньютона, мы найдем шесть знаков корня, если это требуется.
Как пользоваться практически предлагаемой машиной, видно из следующего примера.
Пример. Требуется .решить уравнение:
32жЗ 4- ей - 37А- - 88 О
Корни этого уравнения, как известно, по абсолютной величине меньше
1+1 4.
При этом положительных корней не больше 1 (одна перемена знаков в коэфициентах Л ц, А, А, АЯ). Следовательно, установив соленоиды Х, А, X, Х соответственно на расстояниях, пропорциональных коэфициентам, и, поставив соответственно соленоиды 7, 1, 1, 7, на рейке ММ (как указано на фиг. 2), следует переключателем LLi поочередно включить секции с номерами 1, 2, 3. Если, допустим, достигнуто наилучшее равновесие на втором номере, т. е. при JC 2, то оценив приближенно по шкале Р вторую цифру корня, можно уточнить ее, включая промежуточные деления около второго основного; при этом третий знак корня можно оценить приблизительно по шкале пружинки Р.
Заменив х на (--х} и расставив соленоиды пропорционально коэфициентам полученного уравнения
- 32л;« + 81.x: 4- 37л - 88 О,
мы также найдем числовые значения отрицательных корней, которых, очевидно, не больше двух и каждый из которых по абсолютной величине меньше 4. Если же перемещением ползунка переключателя , по всем выводам секции 1-4 не достигнуто равновесие, то это будет означать, что остальные два корня - числа комплексные (их можно
этом случае найти из соотношении iete, механически же мнимых корней айти нельзя)...-,,
Предмет изобретения.
1.Машина для решения уравнений ысших степеней с одним неизвестным, остоящее из парных электромагнитньк соленоидов, расположенных один против ругих, причем одни соленоиды в каждой паре устроены передвижными на рейке, вращающейся около некоторой точки, на расстояниях от этой точки, пропорциональных коэфициентам при неизвестном и свободному члену уравнения, а вторые соленоиды в каждой паре уст|Х ены передвижными на неподвижной рейке, отличающаяся тем, что соленоиды X, Х, Л ..., укрепленные на неподвижной рейке NNi, состоят каждый из девяти секций, из которых первая имеет число витков, равное числу витков в соленоидах / на подвижной рейке М.М. а также в соленоиде Х° на рейке NNi, а последующие имеют число витков в ответвлениях, относящиеся к числу витков в ответвлении первой секции, как
1:2:3: 9, соответственно -: 2: 3:...
9 и т. д. с вывоцами от каждой секции к переключателю LLi, каковые соленоиды 1, 1.... и Х, X, Х включены в электрическую цепь последовательно.
2.В машине по п. 1 применение для соединения одних из концов реек MMi и MVi пружины Р, несущей указатель на одном конце пружины, подвижной против шкалы, соединенной с другим концом пружины.
3.Форма выполнения машины по п. 1, отличающаяся тем, что переключатели соленоидов Х, X, Х, Х .... выполнены в виде передвижных по рейке NN держателей D,, имеющих контактные пластинки L и сидящих на рамках ККъ которые несут по одной, вращаемой осью, замыкающей цепь контактной пластинке В.
Фиг. 2
.1.
Фиг и, м, f,
i- }: i- Г .
сЬиг.З
-4
1
р%Ж ШШуЖЩ (1 С
-. Xi




Авторы
Даты
1936-08-31—Публикация
1934-10-24—Подача