Изобоетение относится к автоматическому управлению и оегулиоованию и предназначено для идентификации неизвестных параметров и восстановления неизмеряекых фазовых координат электромеханических, электрических и радиотехнических систем различного назначения.
Известно устройство идентификации параметров системы управления, содержащее модель, блоки сравиейия, сумматоры, интеграторы и умножители 1.
Однако данное устройство не позволяет одновременно вычислять неизвестные параметры и неизмеряекше фс1зовые координаты систем управления за наперед заданное время.
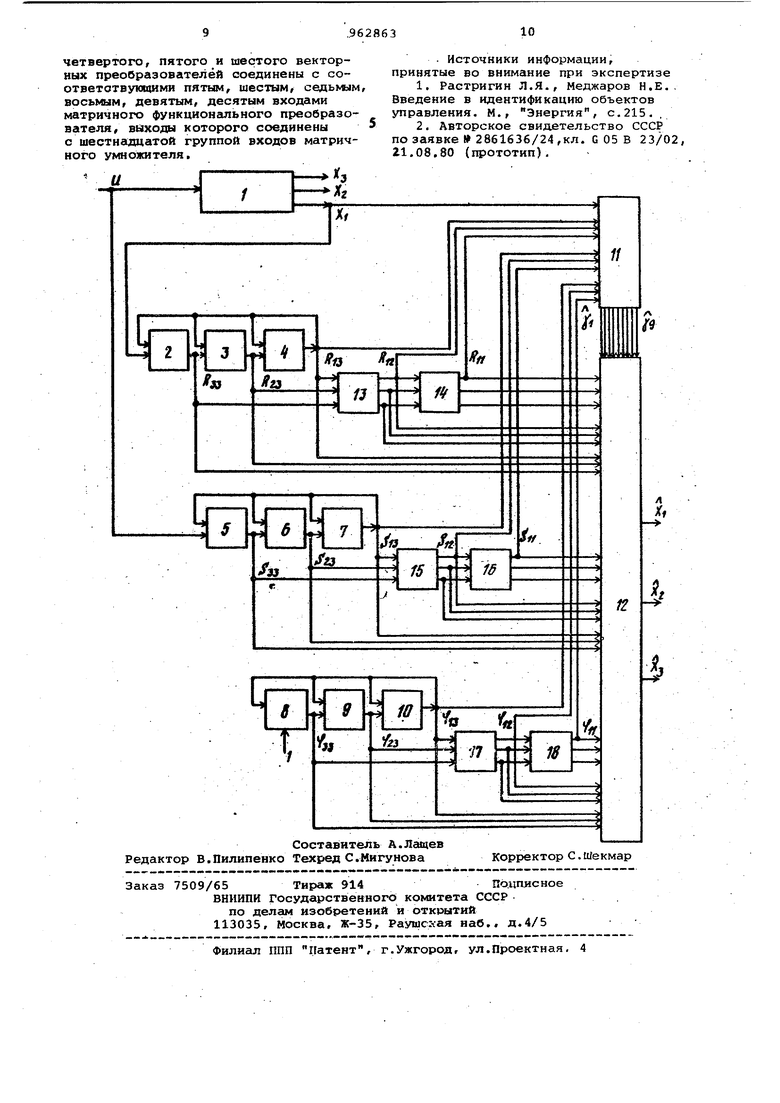
Наиболее близким по технической сущности к предлагаемому является устройство, содержгицее последовательно соединенные объект управления, первый, второй, третий интеграторы и матричный функциональный преобразователь, последовательно соединенные четвертый, пятый и шестой интеграторы, последовательно соединенные седьмой, восьмой и девятый интеграторы, выход девятого интегратора соединен с вторыми входами седьмого, восьмого.
девятого интеграторов и матричного функционального преобразователя, выход шестого интегратора соедине н с вторыми входами четвертого, пятого и шестого интеграторов и третьим входом матричного функционального преобразователя, выход третьего интегратора соединен с вторыми входами первого, второго и третьего интегра10торов, вход объекта управления соединен с первым входом четвертого интегратора, а выход - с первым входом первого интегратора и четвертым входом матричного функционального пре-.
15 образователя 2.
Недостатком известного устройства является невысокая точность при одновременном вычислении за фиксированное время неизвестных параметров и
20 неизмеримых фазовых координат объекта.
Цель изобретения - повышение точности устройства путем одновременного вычисления неизвестных параметров и
25 неиэмеряемых фазовых координат объекта за заданное время.
Для достижения указанной цели идеи тификатор содержит матричный умножитель, последовательно соединенные
30 первый и второй векторные преобразователи, последовательно соединенные третий и 11етвертый векторные преобра зователи, последовательно соединенны пятый и шестой векторные преобразователи, первый вход первого векторно го преобразователя соединен с выходо третьего интегратора и первым входом матричного умножителя, второй вход с выходом второго интегратора и вторым входом матричного умножителя, третий вход - с выходом первого интегратора и третьим входом матричного умножителя, первый вход третьего векторного преобразователя соединен с выходом шестого интегратора и четвертым входом матричного умножителя, второй вход - с выходом пятого интег ратора и пятым входом матричного ум ножителя , третий вход - с выходом четвертого интегратора и шестым входом матричного умножителя. пеоиый вход пятого векторного преобразователя соединен с выходом девятого интегратора и седьмым входом матричного умножителя, второй вход - с выходом восьмого интегратора и восьмым входом матричного умножителя, третий вход - с выходом седьмого интегратора и девятым входом матричного умно жителя, выходы первого, второго, третьего, четвертого, пятого и шеетого векторных преобразователей соединены с соответствующими десятой, одиннадцатой, двенадцатой, тринадцатой, четырнадцатой, пятнадцатой группами входов матричного умножителя , первые выходы первого, второго, третьего, четвертого, пятого и. шестого векторных преобразователей соединены с соответствующими пятым, шестым, седьмым, .-восьмым, девятым, . десятым входами матричного функционального преобразователя, выходы которого соединены с шестнгщцатОй группой входов матричного умножителя На чертеже представлен идеитификатор параметров и состояния объёкта, описываемого дифференциальным уравнением третьего порядка () . Идентификатор содержит объект 1 управления, первую, вторую и тре.тыр цепи из трех последовательно соединенных первого, второго, третьего 2-3-4, четвертого, пятого, шестого 5-6-7 и седьмого, восьмого, девятого 8-9-10 интеграторов, матричный функциональный преобразователь 11, матричный умножитель 12 и три1 цепи из последовательно соединенных векторных преобразователей первого, второго 13-14, третьего, четвертого 15-16 и пятого, шестого 17-18. Выходы матричного функционального преобразователя 11 и выходы матричного умножителя 12 являются выходами устройства, где образуются соответственно оценки неизвестных параметров и f оценки неизмеряемых фазовых координат объекта ( t) , . . Хр (t) . Работу идентификатора параметров и состояния систем управления можно описать математически. Введем обозначения: х (t) х .( t.) , Х2( t) , X jC t ) - вектор состояния объекта 1 (Т - символ транспортирования) , x(t) - измеряемая выходная координ ата объекта 1; U(t) - скалярный вход объекта 1, . 23 вектор выходов интеграторов 4,3,2, стоящих в первой цепи; Sj S i,,Sij, Sj - вектор выходов интеграторов 7,6,5, стоящих во второй цепи; ф -з,,1 1 кт:ор выходов интеграторов 1р, 9, 8, стоящих в третьей цепи; R,j, R-,2 выходы векторного преобразователя 13; R(Rii . OL-i 3i3 выходы векторного преобразователя 14; 5 Ц.. 1 S ttSai - выходы векторных преобразователей 15 и 16 соответственнол Ф « . соответствуклдие выходы векторных преобразователей 17 и 18, -y-lTi-/g вектор оценок неизвестных параметров объекта 1; ,з ,хз) - вектор оценки состояния х« (х, ,х , х) объекта 1. Объект 1 управления описывается уравнением x{t)Ax(t) + bU(t) ,х(0)х... .. , (1) dim , dim. , dim x{t)nxl, dim n(t)lxl. Коэффициенты a,, .. ., a матрицы A и координаты Ь, ..., Ь вектора Ь суть неизвестные постоянные. Неизвестны также координаты начального вектора состояния х(0), ..., х,(0). Приборно измеряется вход п(t) и координа та x(t) вектора .состояния x(t) ( t)- . . . ,х( t)) объекта 1. Остальные фазовые координаты x,(t), X J (t) , . ., () недоступны прямому измерению. Задача идентификатора параметров и состояния состоит в том, чтобы по измерениям входа n(t) и выxoдax(t) объекта 1 управления на наперед заданном интервале времени Л 0, ТТвычис- лить оценки 3,. .,а,,,Ь,.. .b,Xjf.O},,. . Хр(0) неизвестных параметров а,,..,, ап,Ьц,...Ьп, х(0), .-. . , хг,|0) и одновременно получить оценки x(t) ,,.., xn(t) неизМеряемых фазовых координат вектора х(t). Прибавляя к правой части (1) вектор Cx(t) (С - известная, постоянная гурвицева матрица) .и вычитая, пр дем (1) к виду X {t)-С х( t) X t) EbL п (t) Е Р., -Сп-1 - -Сп 0-OJ Е - единичная мaтpицaJ - единичная матрица; (Ci С„-ап)Г; (5-(Ь i) - векторы неизвестных п метров. Непосредственной подстановкой трудно убедиться, что решение ур нения (2) имеет вид х{1)ф(1)хо+К(1)(1)р, где матрицы Ф(1), R(t), S(t) удо воряют уравнениям Ф{1).СФ(1), Ф(0)«Е, R(t)CR(t) x(t)E, R(0)-0, S(t)CS(t)+n(t)E, S(0)0, , d im Ф (t) d imR( t) d imS (t) nxn Запишем выражения для первой стр ки в левой и правой частях уравнения (3). Игдаем x(t)-Lf(t)xi(0)«4n(t) -/ / л V / -tlV т./А ( О )t . . . If in X „ ( О ) Rii( t) AI -. (tW + S(t)p.... (е)|Ь„. Последнее выражение перепишем в более краткой форме e(t)qT(t)y.(5) где e(t)x(t)-i/(t)x;i(0); q(t) (t)...ifin(t)Rn (t)... R(t)S,,(t)...S(t)3 ; (0), ... x(0)ct .. .Af, .. ..i Из (5) неизвестный вектор парамет ров у вычисляется по формуле Т )(3)(6)g(6)dd,(b) о3 . где Т - наперед заданное время. Теперь, когда оценка ,ft неизвестного вектора параметров | получена, восстановление неизмеряемых фазовых координат х ii( t),..., х( t) объекта 1 управления осуществляется по формуле Х(1) Ф(1)Хо + ЙША+91)11. Из (7) видно, что при вычислении оценки x(t) следует проинтегрировать уравнения 4) для получения матриц ф(1) .R(t).S(t) . Интегрирование одного матричного уравнения из систегиы (4) равносильно интегрированию п уравнений относительно .столбцов соответствующих матриц. Так, матричное уравнение . И U)CR (t)x(t)E ; R (0)«0, эквивалентно следующей системе Rj (t)-CRtNt)4x,(t)ti ; () R(0)0(,...,n) где R - 1 -n - столбец матрицы, R/ i -i - столбец единичной матрицы. Соотношения, аналогичные (9), име|ют место для остальных уравнений в системе (4). Всего уравнений типа (9), будет, очевидно, Зп. Однако общее число уравнений, подлежащих интегрированию, можно сократить до трех. Нетрудно видеть, что векторы Р и Е связаны между собой следукхцим со от но-, шением (i«1,...n-1) Аналогичными зависимостями связаны векторы Ф,- , ; + )t i Ф ,-4i, ;ft iCRui; S|«CS. ; (i l ,...n-1) покажем справедливость (11) на примере уравнения (9). Для этого подставим в (9) значение 4 из (10), а также второе из соотношений (11). Имеем -ciRUi «i t)CC.; RUrtO)- (2) Умножат обе части уравнения (12) слева на матрицу cr(/det С/ /Сп/; 0), получаем (t)-CRUi (,(t)-M- (13) Уравнение (13) совпадает с уравнением для (+1)-го столбца матрицы R(t). С помощью соотношений (11) аналогично осуществляется переход от уравнения (13) к (9). Таким образом, вместо интёгрирования 3 уравнений (4) достаточно проинтегри1)овать три, а именно Rn(t)-CRf,(t) + x(t)n,Rn(0)-0 Sn(t)CSn(t)+n(t)«n. Sn(0)«0 (11.) Ф(1)-сФп(1).Ф„(о).д«,гп(о..-о1) , rfleRn(t), 5п(.1),Фп(1) n-e столбцы размерна nxl матриц R(t), S(t),4(t). Интегрирование уравнений (14) при , осуществляют первая, вторая и третья цепи из последовательно соединенных интеграторов 2-3.-4. 5-6-7,8-910. На интеграторе 8 задаются начальные условия УЗЗ() Один вход ИН-тегратора 2 соединен с выходом объ екта 1 управления, а один вход интегратора 5 соединен с входом объекта 1 упрзаленйя. На выходах интеграторов каждрй цепи образуются вектода )Kз(tl.iCt).r,tt)V Ri(,«2i( l S li Si rTpH цепи из последовательно соеди ненных векторных преобразователей 13 14, 15-16 и 17-18 осуществляют вЫчис леяия по формулам (11) при 3с цёлью получения остальных столбцов мат риц 4(t) , R(t) , S(t) . Матричный функциональный преобраэо§атель 11 вычисляет оценку у (xj,o,$) вектора неизвестных napftMcTpOB У по формуле (6 ). Соответствующие входы матричнрго функцио нального преобразователя 11 подключены к выходам интеграторов 4, 7,10, квыходам R,R векторных преобразователей 13, 14, к выходам S , век торных преобразователей 15, 16, к выходам 1, Ч векторных преобразо ватрлей 18, а также к выходу х объекта 1 управления. На выходе матричного функционального преобразователя образуют.ся сигналы, численно равные оценкам XQ,ot , (ь вектора неиз вестных параметров . Матричный умножитель 12 производит вычисление по формуле (7 ). Соответствующие входы матричного умножителя 12 соединены с выходами интегра торов 2-10, векторных преобразователей 13-18 и с выходами матричного функционального преобразователя 11. На выходе матричного умножителя 12 образуются сигналы, численно равные оценкам неизмеряемых фазовых координат a(t), з(). Изобретение позволяет существенно повысить точность управления за счет вычисления оценок координат вектора состояния и неизвестных параметров за заданное время, которое может быть значительно меньше времени пере ходного процесса объекта управления, Изобретение расширяет область при менения идентификаторов и может найти применение для управления объектами с неизвестными параметрами при неполной информации о координатах вектора состояния. Кроме повышения точности и расширения области применения предлагаемый идентификатор позволяет упростить первоначальную накладку систем управления и снизить эксплуатационные расходы. Формула изобретения Идентификатор параметров и состоя ния систем управления, содержащий последовательно соединенные объект упрлаленкяf первый, второй, третий интеграторы и матричный функциональный преобразователь, последовательно соединенные четвертый, пятый и шестой интеграторы, последовательно соединенные седьмой, восьмой и девятый интеграторы, выход девятого интегратора соединен с вторыми входами седьмого, восьмого, девятого интеграторов и матричного функционального преобразователя, выход шестого интегратора соединен с вторыми входами четвертого, пятого и шестого интеграторов и третьим входом матричного функционального преобразователя, выход третьего интегратора соединен с вторыми входами первого, второго и третьего интеграторов, вход объекта управления соединен с первым входом четвертого интегратора, а выход - с первым входом первого интегратора и четвертым входом матричного функционального преобразователя, отличающийся тем, что, с целью повышения точности идентификатора путем одновременного вычисления неизвестных параметров и неизмеряемых фазовых координат объекта за заданноевремя, в него введены матричный умножитель, последовательно соединенные первый и второй векторные преобразователи, последовательно соединенные третий и четвертый векторные преобразователи, последовательно соединенные пятый и шестой векторные преобразователи , первый вход первого векторного преобразователя соединен с выходом третьего интегратора и первым входом матричного умножителя, второй вход с выходом второго интегратора и входом матричного умножителя, третий вход - с выходом первого ин.тегратора и третьим входом матричного умножителя, первый вход третьего векторного преобразователя соединен с выходом шестого интегратора и четвертым входом матричного умножителя,второй вход - с выходом пятого интегратора и пятым входом матричного умножителя, третий вход - с выходом четвертого интегратора и шестым входом матричного умножителя, первый вход пятого векторного преобразователя соединен с выходом девятого интегратора и седьмым входом матричного умножителя, второй вход - с выходом восьмого интегратора и восьмым входом матричного умножителя, третий вход - с выходом седьмого интегратора и девятым входом матричного умножителя, выходы первого, второго, третьего, четвертого, пятого и шестого векторных преобразователей соединены с соответствующими десятой, одй ннадцатой, двенадцатой, тринадцатой, четырнадцатой, пятнадцатой группами входов матричного умножителя, первые входы первого, второго, .третьего.
четвертого, пятого и шестого векторных преобразователей соединены с соответотвующими пятым, шестым, седьмым, восьмым, девятым, десятым входами матричного функционального преобразователя, выходы которого соединены с шестнадцатой группой входов матричного умножителя.
Источники информации, принятые во внимание при экспертизе
1.Растригин Л.Я., Меджаров Н.Е.. Введение в идентификацию объектов управления. М., Энергия, с.215.
2.Авторское свидетельство СССР по заявке 2861636/24,кл. G 05 В 23/02, 21.08,80 (прототип).



| название | год | авторы | номер документа |
|---|---|---|---|
| Идентификатор параметров стохастического динамического объекта | 1984 |
|
SU1255991A1 |
| Способ регулирования мощности емкостной компенсации в тяговой сети | 1987 |
|
SU1504723A1 |
| Устройство для преобразования координат @ точек | 1980 |
|
SU960854A1 |
| КОМБИНИРОВАННЫЙ СПОСОБ ФОРМИРОВАНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА И НАБЛЮДАЕМОГО С ЕГО БОРТА ОБЪЕКТА В СТАБИЛИЗИРОВАННОЙ СИСТЕМЕ КООРДИНАТ, КОМПЛЕКСНАЯ СИСТЕМА ЕГО РЕАЛИЗАЦИИ | 2001 |
|
RU2207513C1 |
| Следящая система автоматического управления нестационарным динамическим объектом | 2018 |
|
RU2692204C1 |
| Устройство для формирования сигнала управления с оптимальными коэффициентами обратной связи | 1984 |
|
SU1242913A1 |
| Устройство для идентификации параметров систем управления | 1979 |
|
SU885976A1 |
| Система терминального управления пространственным угловым маневрированием | 1988 |
|
SU1613999A1 |
| ПАССИВНАЯ ПЕЛЕНГАЦИОННАЯ СИСТЕМА | 2005 |
|
RU2298803C2 |
| Устройство для вычисления координат | 1989 |
|
SU1635178A1 |


Авторы
Даты
1982-09-30—Публикация
1981-03-18—Подача