Изобретение относится к области управления технологическими процессами и может быть использовано при управлении инерционным объектом с экстремальной статической характеристикой, состоящей из двух монотонных промежутков, сопряженных в точке экстремума. Последняя представляет собой минимальное либо максимальное значение выходной координаты этой характеристики. Задача управления в этом способе состоит в достижении и удержании экстремума статической характеристики в ходе технологического процесса, а качество управления может оцениваться средней амплитудой колебаний выходной координаты объекта и средней величиной отклонения текущего значения этой координаты от экстремума.
Целью изобретения является повышение качества управления за счет увеличения средней скорости управляющего воздействия путем выбора минимально допустимого периода его изменений.
Цель достигается тем, что по способу, включающему измерения выходного сигнала объекта управления и по результатам их анализа периодические дискретные изменения управляющего воздействия, на объект управления вначале последовательно подают первое и второе различные по величине неизменные пробные управляющие воздействия и после поочередного вывода объекта на соответствующие указанным воздействиям установившиеся режимы регистрируют определяющие эти режимы значения выходного сигнала, затем определяют среднее из упомянутых значений выходного сигнала и в заданный момент времени опять подают на объект управления первое пробное воздействие, после чего, когда объект управления начнет возвращаться к своему первому установившемуся режиму, непрерывно контролируют текущее значение выходного сигнала, фиксируют момент достижения равенства его с ранее определенным средним и в качестве периода изменений управляющего воздействия выбирают величину, равную или большую разности между зафиксированным и заданным моментами времени. Для предотвращения возможных ошибок при реализации способа в процессе вывода объекта управления на соответствующий второму пробному воздействию установившийся режим дополнительно контролируют монотонность изменения, т. е. неизменность знака скорости выходного сигнала, и при ее нарушении возобновляют осуществление способа, принимая второе пробное воздействие за новое первое. При возникновении потребности в корректировке величины выбранного периода указанные операции выполняют снова.
На фиг.1 представлена структурная схема системы, реализующей способ; на фиг. 2 показано поведение этой системы при двух различных значениях периода изменений управляющего воздействия.
Система содержит объект управления, линейная инерционная часть 1 которого с передаточной функцией Wo(p) соединена выходным сигналом x с нелинейной безынерционной частью 2 объекта со статической характеристикой вида у=Кх2 (экстремум здесь является минимумом), и подключенный к выходу объекта экстремальный регулятор 3, состоящий из последовательно соединенных импульсного элемента 4, входным сигналом для которого служит выходной сигнал у нелинейной части 2 объекта, и исполнительного устройства (интегратора) 5 с передаточной функцией Wu(р)=1/p, выходной сигнал u которого подан на вход линейной части 1 объекта управления.
Для описания поведения системы на фиг.1 при двух различных значениях периода изменений управляющего воздействия Та и Тб на фиг.2 приняты следующие обозначения: хо - начальное, до реверса, значение х, va и vб - серии импульсов с выхода элемента 4, соответствующие этим периодам.
Способ осуществляется следующим образом.
Импульсный элемент 4 формирует и подает на вход интегратора 5 серию импульсов v(t) в соответствии с законом управления
v(t) = 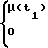
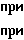
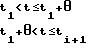 (1)
(1)
μ(t1) = -μ(ti-1){sign[y(ti)-y(ti-1)-χy[}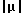 = 1,ti= iT, i=0,1,2,...,, (2) где t - время; θ - длительность импульсов; Т - период повторения импульсов; κу - зона нечувствительности регулятора. Конкретный вид экстремума - минимум - влияет только на знак перед правой частью выражения (2) и не нарушает общности последующих рассуждений. Выходной сигнал интегратора 5 представляет собой последовательность единичных ступенчатых воздействий u(t), которая поступает на вход линейной части 1 объекта управления.
= 1,ti= iT, i=0,1,2,...,, (2) где t - время; θ - длительность импульсов; Т - период повторения импульсов; κу - зона нечувствительности регулятора. Конкретный вид экстремума - минимум - влияет только на знак перед правой частью выражения (2) и не нарушает общности последующих рассуждений. Выходной сигнал интегратора 5 представляет собой последовательность единичных ступенчатых воздействий u(t), которая поступает на вход линейной части 1 объекта управления.
Как видно из фиг.2, поведение системы определяется эволюциями выходной координаты х(t) линейной части 1 объекта на интервале времени между моментом t1 подачи реверсирующего сигнала и моментом t1+1измерения реакции объекта на его воздействие.
В том случае, если удовлетворяется условие
{ [x(ti+1)-x(ti)] sign(xo)} - κx, (3) где κх - величина, определяемая чувствительностью регулятора, - она связана известным соотношением с величиной κу из выражения (2), то в момент t1+1 знак управляющего воздействия не изменяется, так как величина [y(ti)-y(ti-1)- κy] в выражении (2) отрицательна. Как видно из фиг.2, этот факт имеет место, если период изменения управляющего воздействия равен Та>Тб. В этом случае система делает очередной (i+2)-й шаг в том же направлении, что и предыдущий, т.е. к экстремуму.
В случае, если период равен Тб<Та и условие (3) не выполняется, то и величина [y(ti)-y(ti-1)- κy] в выражении (2) положительна, а значит, в момент ti+1 снова происходит реверс управляющего воздействия и свой очередной (i+2)-й шаг система делает в сторону от экстремума, что ведет к увеличению ошибки управления, т. е. к понижению его качества. Таким образом, неравенство (3) является условием безошибочной работы системы.
Для определения координаты х(t) в моменты времени ti и ti+1линейный импульсный элемент 4 удобно представить в виде генератора δ-импульсов с периодом Т и формирующего элемента с передаточной функцией Wф(р)=[1-exp(- θp)] /p, преобразующего δ-импульсы в единичные прямоугольные импульсы длительностью θ <<Т. Если теперь выделить приведенную линейную часть системы и обозначить ее передаточную функцию как Wпр(р)=Wф(р)Wo(p), то изображение по Лапласу для величины х можно представить в виде
L{ x(t)} = Wпр(p)
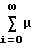 (ti)exp(-pti), а саму реакцию инерционной части системы на последовательность прямоугольных импульсов - в виде
(ti)exp(-pti), а саму реакцию инерционной части системы на последовательность прямоугольных импульсов - в виде
x(t)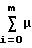 (ti)hпр(t-ti), tm<t≅ tm+1, (4) где hпр(t)=L-1{Wпр(р)} - переходная характеристика приведенной линейной части системы.
(ti)hпр(t-ti), tm<t≅ tm+1, (4) где hпр(t)=L-1{Wпр(р)} - переходная характеристика приведенной линейной части системы.
Если теперь для определенности принять, что κх=0(= κy) и хо<0 (как на фиг.2), и считать, что система после пуска сразу начала двигаться в сторону экстремума, то с учетом выражения (4) неравенство (3) записывается в виде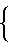
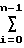 h
h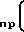 tn+1-t
tn+1-t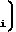 -hпр(tn+1-tn) -
-hпр(tn+1-tn) -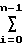 h
h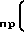 tn-t
tn-t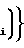 ≅ 0 или
≅ 0 или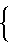
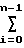 h
h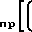 n-i+1
n-i+1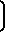 T
T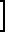 -hпр(T) -
-hпр(T) -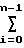 h
h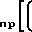 n-i
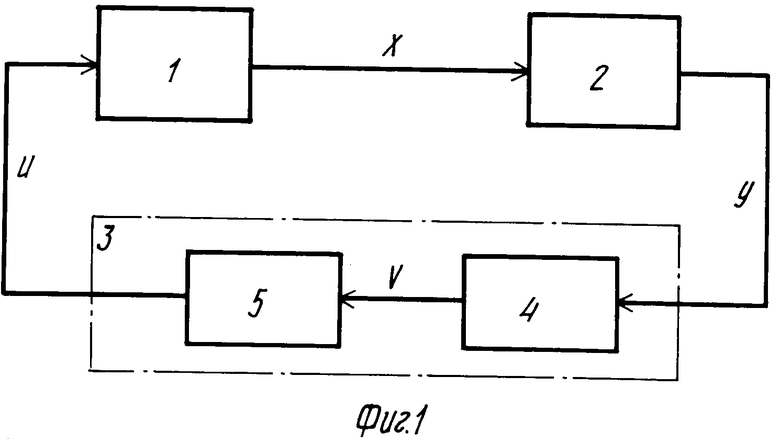
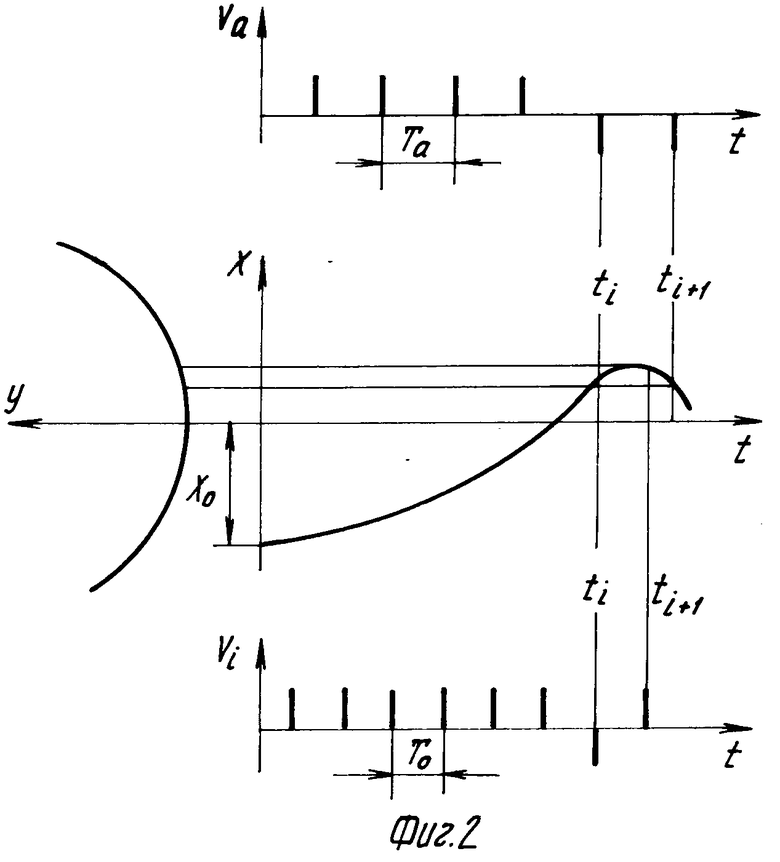
n-i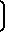 T
T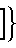 ≅ 0, откуда после несложных преобразований можно получить
≅ 0, откуда после несложных преобразований можно получить
{hпр[(n+1)T]-2hпр[T]} ≅ 0. (5)
Неравенство (5) позволяет выразить условие безошибочной работы через характеристики системы и начальное отклонение ее от экстремума. При заданных параметрах системы, определяющих ее переходную характеристику, и известном начальном отклонении от экстремума минимальная величина периода Т изменения управляющего воздействия, гарантирующая безошибочный переходный процесс, может быть найдена из решения уравнения
2hпр[T] -hпр[(n+1)T]=0, (6) где n=xo/ Δ x+1; Δ x - величина дискретного шага системы.
Как видно из уравнения (6), величина искомого периода Т зависит от начального состояния системы управления, т.е. от числа шагов n, которые необходимо сделать для достижения экстремума. Для решения этого уравнения число n нужно предварительно определить, что представляет известную, а иногда и непреодолимую, трудность, так как, во-первых, необходимо знать начальное состояние системы и положение экстремума и, во-вторых, каждый раз определять их заново. Все это усложняет процедуру определения величины Т. Для упрощения этой процедуры, а главное обеспечения безошибочной работы системы при любых начальных условиях, следует выбрать максимальную величину Т из всех, отвечающих уравнению (6), что соответствует n= ∞, когда уравнение (6) принимает вид
2hпр[T]-hпр[ ∞]=0.
Это означает, что второй член уравнения представляет собой новое установившееся значение переходной характеристики приведенной линейной части системы. Если последнее уравнение записать в виде
hпр[T] = hпр[ ∞]/2, то становится очевидной последовательность операций описанного способа. Действительно, искомая величина Т оказывается равной времени, за которое переходная характеристика hпр достигает половины своего установившегося значения, поэтому при реализации способа сначала определяют установившееся значение, затем его половину и, наконец, время достижения этой половины.
Изложенные соображения основываются на схеме фиг.1 и на возможности измерения входной координаты х экстремальной характеристики. Однако на практике не всегда имеется возможность разделить линейную и нелинейную части объекта управления и непосредственно измерить координату х. Учитывая, что отрезок экстремальной характеристики, к которому относятся эти соображения, можно выбрать достаточно малым за счет соответствующего выбора пробных управляющих воздействий и пренебречь его нелинейностью, т.к. принять, что на этом отрезке у= Сх, где С - некоторый постоянный коэффициент, то все обоснование способа остается в силе при замене х на у, и можно проводить все операции способа, измеряя выходную координату экстремальной характеристики объекта управления, как указано выше.
Предыдущие рассуждения предполагают, что все описанные операции выполняются в пределах одного из монотонных промежутков экстремальной статической характеристики объекта управления, где можно пренебречь ее нелинейностью, что позволяет воспользоваться при обосновании способа линейной теорией переходных процессов. Если в процессе вывода на второй установившийся режим выходной сигнал объекта управления переходит с одного монотонного промежутка на другой, то результат реализации способа ошибочен, т.е. полученная величина Т может оказаться как меньше, так и больше действительно необходимой. В первом случае система работает с ошибками, а во втором - с необоснованно уменьшенной скоростью управляющего воздействия, что в обоих случаях ведет к ухудшению качества управления.
Для предотвращения этой ошибки необходимо, чтобы при обоих установившихся режимах значения выходного сигнала объекта управления находились на одном монотонном промежутке экстремальной характеристики. Для этого в процессе вывода объекта управления на соответствующий второму пробному воздействию установившийся режим следует контролировать монотонность изменения выходного сигнала и в случае ее нарушения, что означает достижение экстремума и переход на сопряженный промежуток, повторить осуществление способа, считая, что в момент обнаружения немонотонности происходит вывод объекта на первоначальный установившийся режим. Тогда второе пробное воздействие, отличающееся от первого на заданную величину, вызывает движение в сторону от экстремума, что гарантирует способ от упомянутой ошибки и обеспечивает правильный выбор искомой величины периода изменений управляющего воздействия.
К преимуществам технического решения относятся его простота и возможность оперативно корректировать величину периода Т при изменениях режимов работы и динамических характеристик системы управления.
| название | год | авторы | номер документа |
|---|---|---|---|
| КОМАНДНЫЙ БЛОК ДЛЯ ЭКСТРЕМАЛЬНОГО РЕГУЛЯТОРА | 2011 |
|
RU2475797C1 |
| СПОСОБ АДАПТАЦИИ ИНТЕРВАЛА КВАНТОВАНИЯ В ДИСКРЕТНЫХ ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ С ПОСТОЯННОЙ ДЛИНОЙ ШАГА | 1973 |
|
SU397889A1 |
| Способ поиска экстремума | 1978 |
|
SU744447A1 |
| СПОСОБ ПОИСКА ЭКСТРЕМУМА СТАТИСТИЧЕСКОЙ ХАРАКТЕРИСТИКИ ИНЕРЦИОННОГО ОБЪЕКТА | 2011 |
|
RU2471220C1 |
| Устройство для регулирования колебаний виброплощадки | 1981 |
|
SU987597A1 |
| СПОСОБ ПОИСКА МИНИМУМА | 1973 |
|
SU408272A1 |
| Экстремальный регулятор для резонансного объекта | 1975 |
|
SU590695A1 |
| Многоканальный непрерывно-шаговыйэКСТРЕМАльНый РЕгуляТОР | 1978 |
|
SU813357A1 |
| АДАПТИВНЫЙ РЕЛЕЙНЫЙ РЕГУЛЯТОР | 2011 |
|
RU2462744C1 |
| Экстремальный регулятор для резонансного объекта | 1982 |
|
SU1035564A1 |
Изобретение относится к области управления технологическими процессами и может быть использовано при управлении инерционным объектом с экстремальной статической характеристикой. Задачей изобретения является повышение качества управления за счет увеличения средней скорости управляющего воздействия путем выбора минимально допустимого периода его изменений. Решение этой задачи достигается тем, что по способу управления, включающему измерения выходного сигнала объекта управления и по результатам их анализа периодические целесообразные дискретные изменения управляющего воздействия, на объект управления вначале последовательно подают первое и второе неизменные пробные воздействия и после поочередного вывода объекта на соответствующие им установившиеся режимы регистрируют значения выходного сигнала, затем определяют среднее из этих значений и в заданный момент времени опять подают первое пробное воздействие, после чего контролируют выходной сигнал, фиксируют момент достижения его равенства с ранее определенным средним и выбирают в качестве периода изменения управляющего воздействия величину, равную или большую разности между зафиксированным и заданным моментами времени. Дополнительно при выводе объекта управления на второй установившийся режим контролируют монотонность изменения выходного сигнала и при ее нарушении возобновляют осуществление способа, принимая второе пробное воздействие за новое первое. 1 з.п.ф-лы, 2 ил.
| Фицнер Л.Н | |||
| О принципах построения и методах анализа некоторых типов экстремальных систем | |||
| //Теория и применение дискретных автоматических систем | |||
| Машина для добывания торфа и т.п. | 1922 |
|
SU22A1 |
Авторы
Даты
1994-06-30—Публикация
1991-04-05—Подача