Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании гирокомпасов и курсоуказывающих устройств полуаналитического типа.
Известны способы определения истинного курса с помощью гироскопического датчика угловой скорости (см., например, книгу Б.И.Назарова и Г.А.Хлебникова "Гиростабилизаторы ракет" М. , 1975, стр.193-196 и патент RU 2098766 С1 по кл. G 01 С 21/14 от 10 декабря 1997 г.), согласно которым курсовое направление горизонтально расположенной измерительной оси гироскопа на неподвижном основании определяют аналитически с использованием результатов показаний с гироскопа, полученных на разных азимутальных углах.
За прототип взят способ определения истинного курса с помощью двухканального гироскопического датчика угловой скорости (см. патент RU 2176708 по кл. G 01 C 21/12 от 10 декабря 2001 г.).
В этом способе определения истинного курса с помощью одного гироскопа предварительно привязывают измерительные оси гироскопа к осям, связанным с объектом, применяют гироскоп в режиме обратной связи по току датчика момента, определяют сигналы с эталонных сопротивлений датчика угловой скорости, затем при операции предварительной настройки проводят фазировку системы измерения напряжений с эталонных сопротивлений гироскопа, обеспечивающую отрицательное приращение сигналов с первого и второго каналов гироскопа при азимутальном повороте его корпуса против часовой стрелки на 90o из положения, при котором измерительная ось Y первого канала направлена на север, а измерительная ось Х второго канала на восток, определяют коэффициенты модели дрейфа гироскопа, а при гирокомпасировании в искомом курсовом положении объекта определяют углы наклона плоскости измерительных осей гироскопа по тангажу и крену, угол широты местоположения объекта, напряжения с эталонных сопротивлений гироскопа по первому и второму каналам, а затем определяют значение истинного курса измерительной оси первого канала гироскопа по следующей формуле
K=2π-arctg a, если b1>0, b2>0;
K=π-arctg a, если b1>0, b2<0;
K=π-arctg a, если b1<0, b2<0;
K=-arctg a, если b1<0, b2>0,
где a=b1b2 -1; ,
,
b2 = U11Кн11cosγ+ω
ω
U11, U12 - напряжения с эталонных сопротивлений датчика угловой скорости соответственно по первому и второму каналам,
Kн11, Kн12 - крутизна гироскопа по напряжению для первого и второго каналов,
υ,γ - углы наклона плоскости осей чувствительности гироскопа соответственно по тангажу и крену,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта.
Гирокомпасирование с применением известного способа возможно в условиях неподвижного основания. Угловые движения основания вызывают весьма значительные погрешности гирокомпасирования. Оценить эти погрешности можно расчетным путем, используя следующее выражение для ошибки гирокомпасирования
где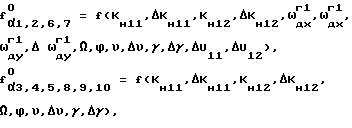
ΔU11, ΔU12 - погрешность измерения напряжений с эталонных сопротивлений датчика угловой скорости соответственно по первому и второму каналам,
ΔKн11, ΔKн12 - погрешность задания крутизны гироскопа по напряжению для первого и второго каналов,
Δυ,Δγ - погрешность задания углов наклона плоскости осей чувствительности гироскопа соответственно по тангажу и крену,
Δϕ - погрешность задания широты местоположения.
Рассмотрим влияние в известном способе на погрешность гирокомпасирования скорости рыскания 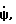 скоростей изменения углов тангажа
скоростей изменения углов тангажа 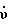 и крена
и крена  при наличии ошибок в задании рассматриваемых параметров. При расчете погрешностей гирокомпасирования с использованием выражения (2) брались следующие значения параметров и ошибок их задания:
при наличии ошибок в задании рассматриваемых параметров. При расчете погрешностей гирокомпасирования с использованием выражения (2) брались следующие значения параметров и ошибок их задания:
ΔU11=ΔU12=0,15 мВ,
Kн11=Kн12=3,5•10-7 1/c мВ,
ΔKн11=ΔKн12=3,5•10-10 1/с мВ,
ω
Δω
ϕ=55,5 град,
Δϕ=0,05 град,
Δυ = Δγ=0,017 град,
υ = γ=30 град.
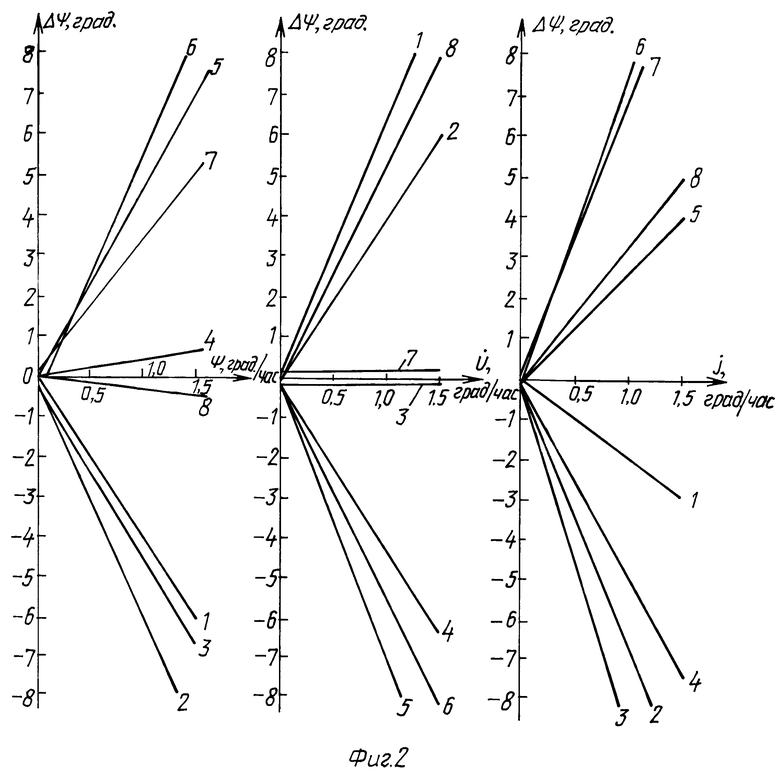
На фиг.2 показаны погрешности гирокомпасирования с помощью двухканального гироскопического датчика угловой скорости в зависимости от скорости рыскания 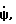 скоростей изменения углов тангажа
скоростей изменения углов тангажа 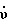 и крена
и крена 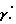 Зависимостями 1, 2, 3, 4, 5, 6, 7, 8 представлены погрешности гирокомпасирования соответственно на азимутальных углах 0, 45, 90, 135, 180, 225, 270, 315o. Эти зависимости показывают, что на разных азимутальных углах угловые скорости рыскания, изменения углов по тангажу и крену обуславливают существенные погрешности гирокомпасирования. Таким образом, известный способ имеет ограничение на применение, обусловленное угловыми скоростями основания.
Зависимостями 1, 2, 3, 4, 5, 6, 7, 8 представлены погрешности гирокомпасирования соответственно на азимутальных углах 0, 45, 90, 135, 180, 225, 270, 315o. Эти зависимости показывают, что на разных азимутальных углах угловые скорости рыскания, изменения углов по тангажу и крену обуславливают существенные погрешности гирокомпасирования. Таким образом, известный способ имеет ограничение на применение, обусловленное угловыми скоростями основания.
Исследуем с применением выражения (2) влияние в известном способе на погрешность гирокомпасирования азимутальной ориентации гироскопа, характеризуемой углом ψ. При расчете этой погрешности гирокомпасирования брались следующие значения параметров и ошибок их задания:
ΔU11=ΔU12=0,15 мВ,
Kн11=Kн12=3,5•10-7 1/c мВ,
ΔKн11=ΔKн12=3,5•10-10 1/с мВ,
Δω
ϕ=55,5 град,
Δϕ=0,05 град,
υ = γ=0,017 град,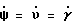 =0,01 град/ч,
=0,01 град/ч,
ω
На фиг. 3 показана погрешность гирокомпасирования с помощью двухканального гироскопического датчика угловой скорости в зависимости от азимутальной ориентации гироскопа.
Из зависимости, представленной на фиг.3, видно, что в известном способе азимутальная ориентация гироскопа влияет на погрешность гирокомпасирования. При этом погрешность имеет синусоидальный характер. Так как в известном способе предполагается бесплатформенная установка гироскопа на объекте, то на различных курсах объекта в этом случае будут различные погрешности гирокомпасирования, которые могут достигать существенных величин на курсовых углах 90 и 270o.
Техническим результатом, который может быть получен при осуществлении настоящего изобретения, является обеспечение возможности гирокомпасирования с применением гироскопических датчиков угловой скорости при наличии угловых скоростей основания и повышение точности гирокомпасирования за счет устранения зависимости погрешности гирокомпасирования от курсового угла.
Технический результат достигается тем, что в известном способе определения истинного курса с помощью двухканального гироскопического датчика угловой скорости, включающем использование гироскопа в режиме обратной связи по току датчиков момента, предварительное согласование знаков изменения напряжений с эталонных сопротивлений гироскопа с направлением поворота корпуса вокруг оси собственного вращения, определение модели дрейфа гироскопа, а при гирокомпасировании определение напряжений с эталонных сопротивлений гироскопа по первому и второму каналам, дополнительно предварительно устанавливают гироскоп на платформу, управляемую в азимуте и стабилизированную в плоскости местного горизонта таким образом, чтобы плоскость измерительных осей гироскопа совпадала с горизонтальной плоскостью платформы, устанавливают платформу на объект так, чтобы ось стабилизации по крену совпадала с продольной осью объекта, ось стабилизации по тангажу была направлена перпендикулярно плоскости симметрии объекта к правому борту, после этого выставляют платформу в горизонте и в азимуте так, чтобы одна горизонтальная ось платформы была направлена на север, другая на восток, поворачивают относительно платформы корпус гироскопа вокруг оси собственного вращения, проводят гирокомпасирование и определение погрешностей гирокомпасирования после поворота, определяют азимутальный угол поворота корпуса гироскопа относительно платформы, при котором погрешность гирокомпасирования минимальна, а затем при рабочем гирокомпасировании определяют азимутальный угол поворота объекта относительно платформы и вычисляют угол истинного курса объекта по следующей формуле
K = 2π-arctg(b1b
K = π-arctg(b1b
K = π-arctg(b1b
K = -arctg(b1b
где b1 = -U12Kн12+ω
b2 = U11Kн11+ω
ω
U11, U12 - напряжения с эталонных сопротивлений датчика угловой скорости соответственно по первому и второму каналам,
Kн11, Kн12 - крутизна гироскопа по напряжению для первого и второго каналов,
ψг - азимутальный угол поворота объекта относительно платформы,
ψг1 - азимутальный угол между горизонтальными осями платформы и гироскопа.
Схема для гирокомпасирования с применением гироскопического датчика угловой скорости, установленного на управляемую в азимуте и стабилизированную в плоскости местного горизонта платформу, представлена на фиг.1.
При анализе этой схемы рассмотрим следующие системы координат. Система координат ОдХдYдZд является системой координат Дарбу: ось ОдХд направлена на север, ось ОдYд - вертикально вверх, а ось ОдZд - на восток. Систему координат ОсXсYсZc свяжем с объектом: начало системы координат помещено в центр масс объекта, оси ОсХс и ОсYс расположены в вертикальной плоскости симметрии объекта, при этом ось ОсХс направлена вдоль оси корпуса объекта, а ось ОсYс - по перпендикуляру к оси ОсХс, лежащему в вертикальной плоскости симметрии объекта, ось OcZc перпендикулярна плоскости симметрии объекта и образует правую систему координат. С платформой свяжем правую ортогональную систему координат ОпХпYпZп: оси ОпYп и OпZп лежат в плоскости платформы, при этом ось ОпХп совпадает с осью стабилизации по крену при совпадении плоскостей платформы и внешнего кольца, ось OпZп направлена по оси стабилизации платформы по тангажу, ось ОпYп перпендикулярна плоскости платформы и направлена по оси платформы. С наружным кольцом карданова подвеса платформы свяжем систему координат O1X1Y1Z1: ось O1X1 направлена по оси внешнего кольца, являющейся осью стабилизации платформы по крену, ось O1Y1 направлена перпендикулярно плоскости кольца, ось O1Z1 совпадает с осью внутреннего кольца и осью стабилизации по крену. С внутренним кольцом свяжем систему координат O2X2Y2Z2: ось O2Z2 направим по оси внутреннего кольца, ось О2Y2 - по оси платформы, ось О2Х2 направлена перпендикулярно плоскости внутреннего кольца. С гироскопом свяжем систему координат Oг1Хг1Yг1Zг1: оси Oг1Xг1 и Oг1Yг1 расположены в измерительной плоскости гироскопа, при этом ось Oг1Xг1 направлена по измерительной оси второго канала, а ось Oг1Yг1 - по измерительной оси первого канала гироскопа, ось Oг1Zг1 направлена вдоль оси собственного вращения гироскопа.
Пусть в начальный момент времени оси, связанные с платформой и объектом, совпадают с системой координат Дарбу. Вследствие углового движения объекта в азимуте со скоростью рыскания  оси, связанные с объектом OcZc и ОсХс, и оси O1Z1 и O1X1, О2Z2 и О2Х2, связанные с кольцами подвеса, повернутся на азимутальный угол ψ.г. От угловых движений объекта по тангажу
оси, связанные с объектом OcZc и ОсХс, и оси O1Z1 и O1X1, О2Z2 и О2Х2, связанные с кольцами подвеса, повернутся на азимутальный угол ψ.г. От угловых движений объекта по тангажу 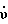 и крену
и крену 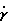 система координат, связанная с объектом, наклонится соответственно на угол тангажа υ и угол крена γ. При этом внешнее кольцо подвеса наклонится на угол тангажа υ.
система координат, связанная с объектом, наклонится соответственно на угол тангажа υ и угол крена γ. При этом внешнее кольцо подвеса наклонится на угол тангажа υ.
Гироскоп работает в режиме обратной связи по токам датчиков момента и является двухканальным датчиком угловой скорости. Первый канал гироскопа содержит датчик угла 1, измеряющий поворот корпуса гироскопа относительно измерительной оси Yг1, усилитель 2, эталонное сопротивление 3, датчик момента 4, создающий момент вокруг оси Xг1. Второй канал содержит датчик угла 5, измеряющий поворот корпуса гироскопа относительно измерительной оси Xг1, усилитель 6, эталонное сопротивление 7, датчик момента 8, создающий момент вокруг оси Yг1. Напряжения U11 и U12, снимаемые с эталонных сопротивлений по первому и второму каналам, подаются в вычислитель 9.
Гироскопический датчик угловой скорости установлен на управляемую в азимуте и стабилизированную в плоскости местного горизонта платформу, кинематическая схема которой показана на фиг.1. Устройство имеет трехосный подвес, состоящий из наружного и внутреннего колец. Во внутреннем кольце установлена стабилизируемая платформа. Ось вращения наружного кольца укреплена в подшипниках, жестко связанных с объектом, и ориентируется параллельно продольной оси объекта. Ось вращения внутреннего кольца укреплена в подшипниках, жестко связанных с наружным кольцом. Стабилизированная платформа имеет свободу вращения по отношению к внутреннему кольцу вокруг оси платформы. Ось вращения платформы укреплена в подшипниках, связанных с внутренним кольцом. Платформа обладает относительно объекта тремя степенями свободы, и поэтому установленный на ней датчик угловой скорости развязан от угловых движений объекта, то есть имеет полную трехосную стабилизацию. С помощью управляющих воздействий обеспечивается угловая скорость платформы относительно инерциальной системы координат. При согласовании осей платформы с осями системы Дарбу и отсутствием линейного движения объекта проекции абсолютной угловой скорости платформы на ее оси можно представить в виде
ω
ω
ω
В установившемся режиме для изодромной обратной связи напряжения с эталонных сопротивлений гироскопического датчика угловой скорости можно представить в следующем виде
U11 = (-ω
U12 = (ω
где ω
Пусть платформа с гироскопами расположена на объекте, не имеющем линейной скорости относительно поверхности Земли, но совершающем угловое движение со скоростями 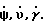 Угловые движения объекта парируются системой стабилизации и на датчики угловой скорости не действуют. Пусть датчик угловой скорости установлен на точную платформу, погрешности стабилизации и дрейф которой малы и ими можно пренебречь. Для этого случая, в соответствии с взаимным расположением выбранных систем координат, проекции абсолютной угловой скорости на оси гироскопа можно представить в следующем виде:
Угловые движения объекта парируются системой стабилизации и на датчики угловой скорости не действуют. Пусть датчик угловой скорости установлен на точную платформу, погрешности стабилизации и дрейф которой малы и ими можно пренебречь. Для этого случая, в соответствии с взаимным расположением выбранных систем координат, проекции абсолютной угловой скорости на оси гироскопа можно представить в следующем виде:
ω
ω
Подставив выражение (6) в (5), можно получить выражения для определения sinψг1 и cosψг1 в следующем виде:
cosψг1 = (U11Kн11+ω
sinψг1 = (-U12Kн12+ω
В практике определения курсового угла с помощью датчика угловой скорости его вычисление проводят через функцию арктангенс. Тогда аналитическое выражение для определения азимутального угла ψг1 можно представить в следующем виде:
ψг1 = arctg(b1b
где b1 = -U12Kн12+ω
b2 = U11Kн11+ω
При использовании функции тангенса квадрант, в котором расположен азимутальный угол ψг1, может быть вычислен по соотношению знаков b1 и b2. Зная квадрант, формулу для вычисления угла истинного курса измерительной оси первого канала гироскопа, можно представить в виде
Kr1=2π-arctg(b1b2 -1), если b1>0, b2>0;
Kr1=π-arctg(b1b2 1), если b1>0, b2<0;
Kr1=π-arctg(b1b2 -1), если b1<0, b2<0;
Kr1=-arctg(b1b2 -1), если b1<0, b2>0. (9)
Учитывая, что угол истинного курса К объекта есть угол, отсчитываемый по часовой стрелке, между осью ОдХд, направленной на север, и проекцией продольной оси объекта ОсХс на горизонтальную плоскость, то есть между направлением оси О2Х2, этот угол можно представить в виде
K = 2π-arctg(b1b
K = π-arctg(b1b
K = π-arctg(b1b
K = -arctg(b1b
где ψг - азимутальный угол поворота объекта относительно платформы,
ψг1 - азимутальный угол между горизонтальными осями платформы и гироскопа.
Азимутальный угол поворота объекта ψг относительно платформы можно определить с помощью датчика угла, расположенного на азимутальной оси платформы.
Азимутальный угол ψг1 между горизонтальными осями гироскопа и платформы выбирается предварительно. Для этого на разных известных азимутальных углах выполняют гирокомпасирование и определяют погрешность гирокомпасирования ΔKг1 и находят угол ψг1, на котором погрешность гирокомпасирования минимальна.
Погрешность гирокомпасирования с применением датчика угловой скорости, установленного на стабилизированную платформу, можно представить в виде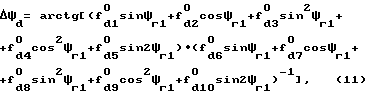
где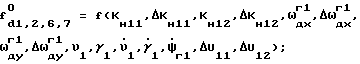
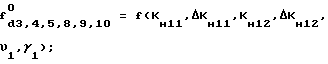
υ1,γ1 - угол наклона платформы по тангажу и крену,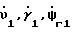 - платформы по крену, тангажу и в азимуте.
- платформы по крену, тангажу и в азимуте.
С помощью выражения (11) исследовалось влияние на погрешность гирокомпасирования азимутального угла ψг1. Исследования проводились путем компьютерных расчетов с использованием следующих параметров и погрешностей их задания:
ΔU11 = ΔU12=0,15 мВ,
υ1 = γ1=0,017 град,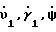 =0,01 град/ч,
=0,01 град/ч,
ω
Δω
ϕ=55,5 град,
Kн11=Kн12=3,5•10-7 1/с мВ,
ΔKн11=ΔKн12=3,5•10-10 1/с мВ,
Δϕ=0,05 град.
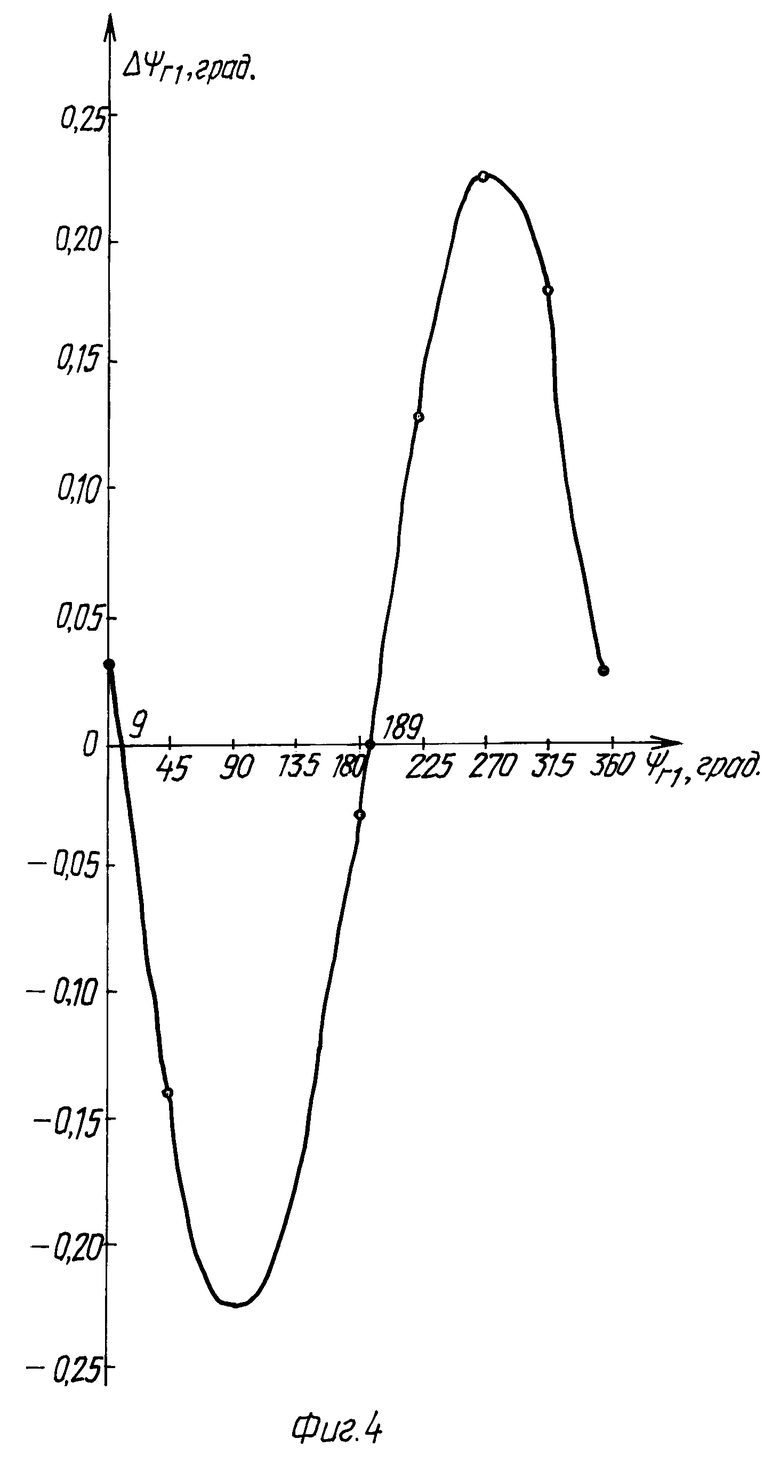
Расчетная погрешность гирокомпасирования ΔKг1 в зависимости от азимутального угла ψг1 между горизонтальными осями управляемой в азимуте и стабилизированной в плоскости местного горизонта платформы и гироскопа показана на фиг.4.
При рассмотрении зависимости, показанной на фиг.4, видно, что есть два азимутальных положения гироскопа при углах ψг1=13,5o и ψг1=148,5o, когда погрешность гирокомпасирования отсутствует. Поэтому выбрав один из этих углов, например, ψг1=13,5o, в этом азимутальном положении фиксируют корпус гироскопа относительно платформы и в дальнейшем при рабочем гирокомпасировании этот угол сохраняется.
Дрейф гироскопа, установленного на платформу, определяется в результате предварительных калибровочных испытаний, по результатам которых строится модель дрейфа, применяемая при гирокомпасировании.
Таким образом, предлагаемый способ гирокомпасирования с применением гироскопического датчика угловой скорости, установленного на управляемую в азимуте и стабилизированную в плоскости местного горизонта платформу, имеет следующие отличия от известного способа:
- в операции предварительной настройки устанавливают гироскопический датчик угловой скорости на платформу, управляемую в азимуте и стабилизированную в плоскости местного горизонта,
- в операции предварительной настройки находят азимутальное положение гироскопа относительно платформы, при котором погрешность гирокомпасирования минимальна,
- в операции гирокомпасирования определяется новая информация об азимутальном угле поворота объекта относительно платформы,
- определение угла истинного курса объекта производится по новой аналитической зависимости, в которой используется информация об углах, характеризующих азимутальные положения гироскопа и объекта относительно платформы.
На фиг.1 показана схема для гирокомпасирования с применением гироскопического датчика угловой скорости, установленного на управляемую в азимуте и стабилизированную в плоскости местного горизонта платформу.
На фиг.2 показаны погрешности гирокомпасирования с помощью двухканального гироскопического датчика угловой скорости в зависимости от скорости рыскания, скоростей изменения углов тангажа и крена.
На фиг.3 показана погрешность гирокомпасирования с помощью двухканального гироскопиченского датчика угловой скорости в зависимости от азимутальной ориентации гироскопа.
Из зависимостей, представленных на фиг.2, видно, что в известном способе угловые скорости объекта, на котором установлен гироскопический датчик угловой скорости, существенно снижают точность гирокомпасирования, делая ее практически невозможной при угловых скоростях по тангажу, крену и азимуту более чем 1 град/ч.
В предлагаемом способе на датчик угловой скорости угловые скорости объекта в азимуте, по тангажу и крену не действуют, так как он находится на платформе, обеспечивающей трехосную стабилизацию.
Из сравнения зависимостей, представленных на фиг.3 и фиг.4, видно, что в известном способе имеется зависимость погрешности гирокомпасирования от азимутальной ориентации объекта, так как гироскоп бесплатформенным способом жестко связан с объектом. При этом имеются курсовые углы объекта, при которых возникает существенное увеличение погрешности гирокомпасирования.
В предлагаемом способе определяется азимутальная ориентация гироскопа в пространстве, которая обеспечивает минимальную погрешность гирокомпасирования, которая сохраняется во время рабочего гирокомпасирования за счет применения управляемой в азимуте и стабилизированной в плоскости местного горизонта платформы.
Поэтому применение предлагаемого способа позволяет проводить гирокомпасирование с повышенной точностью с применением гироскопического датчика угловой скорости в условиях угловых движений объекта, что невозможно при применении известного способа.
Применение предлагаемого способа позволяет расширить область использования гирокомпасных устройств на основе гироскопического датчика угловой скорости за счет возможности определять истинный курс объекта, подверженного воздействию колебаний грунта, волнения водной поверхности, ветровых нагрузок.

Использование: при создании гирокомпасов и курсоуказывающих устройств полуаналитического типа. Сущность: предварительно устанавливают гироскоп на платформу, управляемую в азимуте и стабилизированную в плоскости местного горизонта таким образом, чтобы плоскость измерительных осей гироскопа совпадала с горизонтальной плоскостью платформы. Устанавливают платформу на объект так, чтобы ось стабилизации по крену совпадала с продольной осью объекта, ось стабилизации по тангажу была направлена перпендикулярно плоскости симметрии объекта к правому борту. Выставляют платформу в горизонте и в азимуте так, чтобы одна горизонтальная ось платформы была направлена на север, другая на восток, поворачивают относительно платформы корпус гироскопа вокруг оси собственного вращения. Проводят гирокомпасирование и определение погрешностей гирокомпасирования после поворота. Определяют азимутальный угол поворота корпуса гироскопа относительно платформы, при котором погрешность гирокомпасирования минимальна. Затем при рабочем гирокомпасировании определяют азимутальный угол поворота объекта относительно платформы. Вычисляют с помощью аналитического выражения угол истинного курса объекта, используя информацию об азимутальном положении объекта и гироскопа относительно платформы. Технический результат: возможность гирокомпасирования при наличии угловых скоростей основания, повышение точности. 4 ил.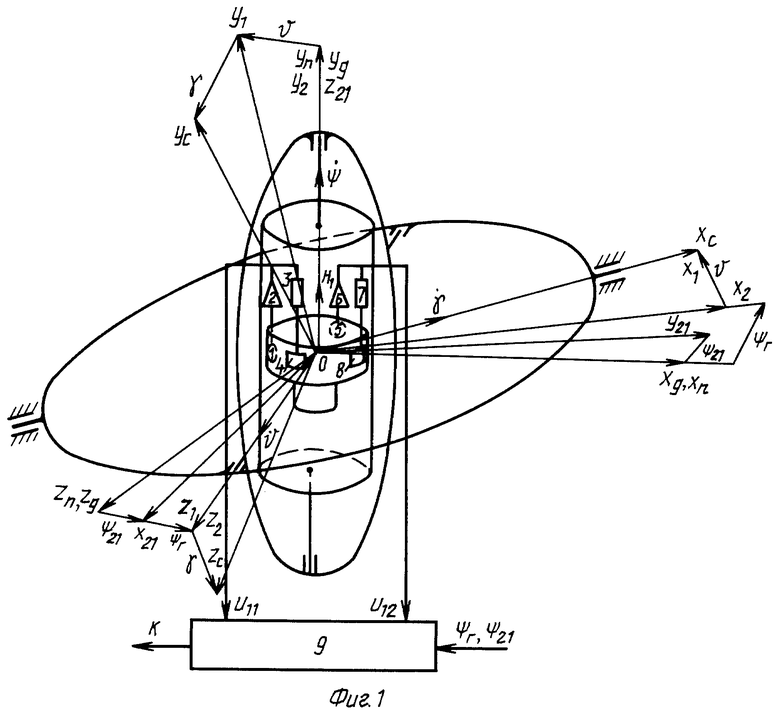
Способ гирокомпасирования с применением гироскопического датчика угловой скорости, установленного на управляемую в азимуте и стабилизированную в плоскости местного горизонта платформу, включающий использование гироскопа в режиме обратной связи по току датчиков момента, предварительное согласование знаков изменения напряжений с эталонных сопротивлении гироскопа с направлением поворота корпуса вокруг оси собственного вращения, определение модели дрейфа гироскопа, а при гирокомпасировании - определение напряжений с эталонных сопротивлений гироскопа по первому и второму каналам, отличающийся тем, что предварительно устанавливают гироскоп на платформу, управляемую в азимуте и стабилизированную в плоскости местного горизонта таким образом, чтобы плоскость измерительных осей гироскопа совпадала с горизонтальной плоскостью платформы, устанавливают платформу на объект так, чтобы ось стабилизации по крену совпадала с продольной осью объекта, ось стабилизации по тангажу была направлена перпендикулярно плоскости симметрии объекта к правому борту, после этого выставляют платформу в горизонте и в азимуте так, чтобы одна горизонтальная ось платформы была направлена на север, другая на восток, поворачивают относительно платформы корпус гироскопа вокруг оси собственного вращения, проводят гирокомпасирование и определение погрешностей гирокомпасирования после поворота, определяют азимутальный угол поворота корпуса гироскопа относительно платформы, при котором погрешность гирокомпасирования минимальна, а затем при рабочем гирокомпасировании определяют азимутальный угол поворота объекта относительно платформы и вычисляют угол истинного курса объекта по следующим формулам:
K = 2π-arctg(b1b
K = π-arctg(b1b
K = π-arctg(b1b
K = -arctg(b1b
где b1 = -U12Kн12+ω
b2 = U11Kн11+ω
ω
U11, U12 - напряжения с эталонных сопротивлений датчика угловой скорости соответственно по первому и второму каналам;
Кн11, Кн12 - крутизна гироскопа по напряжению для первого и второго канала;
ψr - азимутальный угол поворота объекта относительно платформы;
ψr1 - азимутальный угол между горизонтальными осями платформы и гироскопа.
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА С ПОМОЩЬЮ ДВУХКАНАЛЬНОГО ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 2000 |
|
RU2176780C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА С ПОМОЩЬЮ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 1995 |
|
RU2098766C1 |
| US 4458426 А, 10.07.1984 | |||
| US 4622646 А, 11.11.1986. | |||
Авторы
Даты
2003-08-20—Публикация
2002-01-30—Подача