Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании гирокомпасов аналитического типа.
Известны способы определения истинного курса с помощью гироскопического датчика угловой скорости (см., например, книгу Б.И.Назарова и Г.А.Хлебникова "Гиростабилизаторы ракет" М., 1975, стр.193-196 и патент RU 2176708, кл. G 01 C 21/12 от 10 декабря 2001 г.), согласно которым курсовое направление измерительной оси гироскопа на неподвижном основании определяют аналитически. В книге Б.И.Назарова и Г.А.Хлебникова "Гиростабилизаторы ракет" гирокомпасирование выполняется в условиях горизонтального основания с использованием одного канала гироскопа. В патенте RU 2176708 гирокомпасирование возможно проводить в условиях наклонного основания, но при этом используются два канала гироскопа.
Использование одного канала имеет положительное качество, связанное с тем, что при горизонтальном основании не требуется информация о коэффициенте крутизны гироскопа по напряжению, в результате чего исключается существенная ошибка гирокомпасирования, связанная с ошибкой определения этого коэффициента.
За прототип взят способ определения истинного курса с помощью гироскопического датчика угловой скорости при использовании одного канала (см. патент RU 2098766 С1, кл. G 01 C 21/14 от 10 декабря 1997 г.).
В этом способе определения истинного курса с помощью гироскопического датчика угловой скорости предварительно выставляют измерительные оси гироскопа в горизонт и привязывают их к продольной оси объекта, применяют гироскоп в режиме обратной связи по току датчика момента, определяют сигналы с эталонного сопротивления датчика угловой скорости на угле измеряемого курса и положениях, полученных в результате азимутального поворота гироскопа на 90 градусов и 180 градусов, проводят фазировку системы измерения напряжения с эталонного сопротивления обратной связи с направлением поворота корпуса гироскопа, а при гирокомпасировании поворачивают гироскоп в азимуте относительно искомого курсового направления против часовой стрелки на 360 градусов, при этом измеряют углы поворота корпуса гироскопа и соответствующие этим углам напряжения с эталонного сопротивления, затем определяют значения напряжений с эталонного сопротивления в равноотстоящих по углу друг от друга положениях, угловое расстояние между которыми выбирают таким, чтобы для него угол 90 градусов являлся кратным, и определяют значение истинного курса оси гироскопа по следующей формуле:

где
ψi=2π-[arctg((Uj-U(j+0,5N))(2U(j+0,25N)-Uj-U(j+0,5N))-1)-(j-1)2πN-1],
если
Uj-U(j+0,5N)>0, 2U(j+0,25N)-Uj-U(j+0.25N)>0,
ψi=π-[arctg((Uj-U(j+0,5N))(2U(j+0,25N)-Uj-U(j+0.5N))-1)-(j-1)2πN-1],
если
Uj-U(j+0.5N)>0, 2U(j+0,25N)-Uj-U(j+0,25N)<0,
ψi=π-[arctg((Uj-U(j+0,5N))(2U(j+0.25N)-Uj-U(j+0,5N))-1)-(j-1)2πN-1],
если
Uj-U(j+0,5N)<0, 2U(j+0,25N)-Uj-U(j+0,25N)<0,
ψi=-[arctg((Uj-U(j+0,5N))(2U(j+0,25N)-Uj-U(j+0,5N))-1)-(j-1)2πN-1],
если
Uj-U(j+0.5N)<0, 2U(j+0,25N)-Uj-U(j+0,25N)>0,
i - текущий индекс, характеризующий азимутальное положение гироскопа,
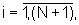
N=2πΔϕ-1 - число угловых разбиений на промежутке [0,2π],
Δϕ - угол между равноотстоящими азимутальными положениями,
N+1 - число измерений на угловом промежутке [0,2π], включая измерения на границах,
Uj=Ui при j≤(N+1),
Uj=U(i-N) при j>(N+1),
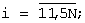
Ui - значение напряжения с эталонного сопротивления датчика угловой скорости в i азимутальном положении.
В известном способе имеются недостатки, снижающие точность гирокомпасирования и связанные с тем, что неточная угловая выставка гироскопа на объекте и наклоны объекта вызывают существенные погрешности гирокомпасирования.
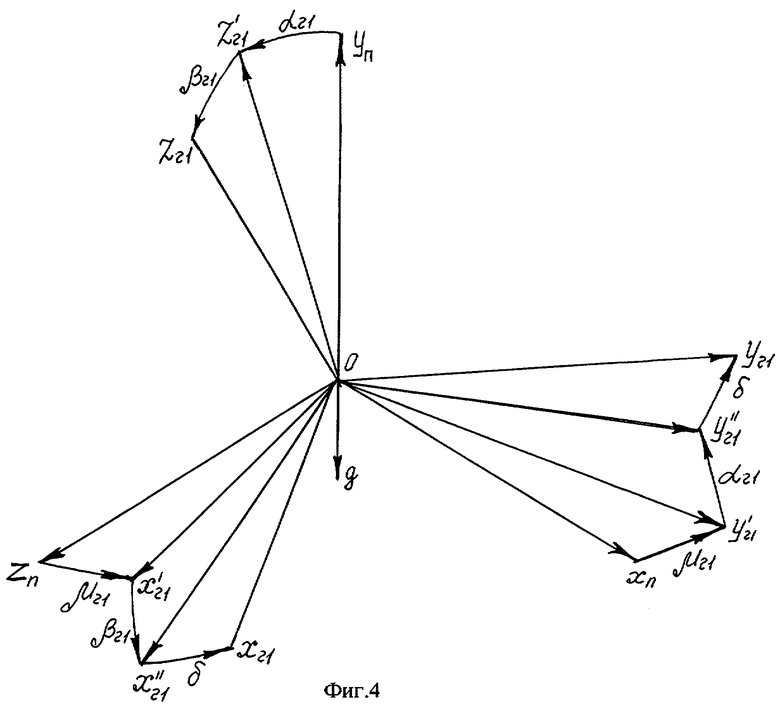
При гирокомпасировании с применением гироскопического датчика угловой скорости определяется азимутальная ориентация одной из его измерительных осей. Практически согласование осей, связанных с гироскопом Xг1Уг1Zг1, и осей, связанных с объектом или корпусом прибора XпУпZп, выполняется с угловыми погрешностями μг1, αг1, βг1, как показано на фиг.4.
На фиг.1 зависимостями 1, 2, 3 показаны расчетные погрешности гирокомпасирования на нулевом курсовом угле при горизонтальном основании с применением известного способа при наличии соответственно угловых невыстовок μг1, αг1, βг1. При расчетах использовались типичные параметры дрейфа гироскопов типа динамически настраиваемых гироскопов. Величина азимутальной невыставки гироскопа μг1 обуславливает погрешность гирокомпасирования, величина которой равна этой погрешности невыставки. Наклон гироскопа на углы αг1 или βг1 также обуславливает погрешности гирокомпасирования, вызванные появлением на измерительной оси гироскопа вредной проекции вертикальной составляющей угловой скорости Земли и дрейфа, не компенсируемого в известном способе, например дрейфа от разбаланса вдоль оси собственного вращения.
Наклон самого объекта по тангажу υ и крену γ также обуславливает погрешности гирокомпасирования по своей физической природе, аналогичные погрешностям от угловых невыставок αri и βri гироскопа в корпусе прибора.
При значительных углах наклона объекта гирокомпасирование с применением известного способа не представляется возможным вследствие возникновения больших погрешностей гирокомпасирования.
Техническим результатом, который может быть получен при осуществлении настоящего изобретения, является повышение точности гирокомпасирования с применением гироскопического датчика угловой скорости.
Технический результат достигается тем, что в известном способе определения истинного курса с помощью гироскопического датчика угловой скорости, включающем предварительную установку гироскопа в исходное положение, при котором измерительная ось Уг1 первого канала гироскопа совпадает с погрешностью установки с продольной осью объекта Хс, измерительная ось Xг1 второго канала гироскопа совпадает с погрешностью установки с направленной к правому борту объекта осью Zc, а ось собственного вращения гироскопа Zг1 направлена с погрешностью установки по оси объекта Ус, находящейся в плоскости его симметрии, работу гироскопа в режиме обратной связи по току датчика момента, фазировку сигнала с эталонного сопротивления с направлением поворота корпуса гироскопа вокруг оси собственного вращения, определение коэффициентов модели дрейфа гироскопа, а при гирокомпасировании определение углов наклона объекта по тангажу и крену, угла широты местоположения объекта, поворот корпуса гироскопа вокруг оси собственного вращения относительно исходного положения против часовой стрелки с измерением углов поворота корпуса гироскопа и напряжений с эталонного сопротивления первого канала в равноотстоящих по углу друг от друга положениях, угловое расстояние между которыми выбирают таким, чтобы для него угол 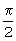 радиан являлся кратным, дополнительно при гирокомпасировании в первом исходном положении определяют углы наклона плоскости измерительных осей гироскопа относительно плоскости объекта, связанной с его продольной осью Хс и осью Zc, направленной к правому борту, потом снимают показания с первого канала гироскопа на заданных углах поворота корпуса гироскопа вокруг оси собственного вращения и возвращают гироскоп в исходное положение, после чего разворачивают корпус гироскопа вокруг продольной оси объекта на угол, равный π радиан, во второе положение и снимают показания с первого канала гироскопа на заданных углах поворота гироскопа вокруг оси собственного вращения, а затем находят угол истинного курса объекта по следующей формуле:
радиан являлся кратным, дополнительно при гирокомпасировании в первом исходном положении определяют углы наклона плоскости измерительных осей гироскопа относительно плоскости объекта, связанной с его продольной осью Хс и осью Zc, направленной к правому борту, потом снимают показания с первого канала гироскопа на заданных углах поворота корпуса гироскопа вокруг оси собственного вращения и возвращают гироскоп в исходное положение, после чего разворачивают корпус гироскопа вокруг продольной оси объекта на угол, равный π радиан, во второе положение и снимают показания с первого канала гироскопа на заданных углах поворота гироскопа вокруг оси собственного вращения, а затем находят угол истинного курса объекта по следующей формуле:
К=0,5(K1+К2), при К<2π,
К=0,5(K1+К2)-2π при К≥2π, (2)
где
K1, К2 - значения курсовых углов, осредненных по углу поворота гироскопа вокруг оси собственного вращения соответственно до и после разворота корпуса гироскопа вокруг продольной оси объекта,
i, j, n - текущие индексы, характеризующие положения гироскопа при его поворотах вокруг оси собственного вращения,
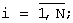
N=2πδ-1 - число измерений на интервале [0,2π) радиан,
δ=δi+1-δi - угол между i и i+1 положениями гироскопа,
j=i+0,5N при i≤0,5N,
j=i-0,5N при i>0,5N,
n=i+0,25N при i≤0,75N,
n=i-0,75N при i>0,75N,

к1i=2π-arctg(a1ib-1 1i), если a1i>0, b1i>0;
к1i=π-arctg(а1ib-1 1i), если а1i>0, b1i<0;
к1i=π-arctg(a1ib-1 1i), если a1i<0, b1i<0;
к1i=-arctg(a1ib-1 1i), если a1i<0, b1i>0, K1i>μ;
к1i=2π-arctg(a1ib-1 1i), если а1i<0, b1i>0, K1i≤μ;
к2i=2π-arctg(a2ib-1 2i), если а2i>0, b2i>0;
к2i=π-arctg(a2ib-1 2i), если a2i>0, b2i<0;
к2i=π-arctg(a2ib-1 2i), если а2i<0, b2i<0;
к2i=-arctg(a2ib-1 2i), если a2i<0, b2i>0; K2i>μ;
к2i=2π-arctg(a2ib-1 2i), если а2i<0, b2i>0; K2i≤μ;
μ - максимально возможная величина азимутальной невыставки гироскопа,
a1i=[(U11i+U11j-2U11n)Kн11(e21cosδi-e11sinδi)-(U11i-U11j)Kн11(e21sinδi+е11cosδi)-Δωг1 д1i·(e21cosδi-e11sinδi)-Δωг1 д2i(e21sinδi+e11cosδi)-2 Ωsinϕ(e13e21-е11е23)]·[2 Ωcosϕ(е12е21-e11e22)]-1;
b1i=[(U11i-U11j)Kн11(e22sinδi+e12cosδi)-(U11i+U11j-2U11n)Kн11(e22cosδi-е12sinδi)+Δωг1 д2i·(e22sinδi+e12cosδi)+Δωг1 д1i(e22cosδi-e12sinδi)-2 Ωsinϕ(e12e23-е13е22)]·[2 Ωcosϕ(е12е21-e11e22)]-1;
a2i=[(U21i+U21j-2U21n)Kн11(l21cosδi-l11sinδi)-(U21i-U21j)Kн11(l21sinδi+l11cosδi)-Δωг1 д3i·(l21cosδi-l11sinδi)-Δωг1 д4i(l21sinδi+l11cosδi)-2 Ωsinϕ(l13l21-l11l23)]·[2 Ωcosϕ(l12l21-l11l22)]-1;
b2i=[(U21i-U21j)Kн11(l22sinδi+l12cosδi)-(U21i+U21j-2U21n)Kн11(l22cosδI-l12sinδi)+Δωг1 д4i·(l22sinδi+l12cosδi)+Δωг1 д3i(l22cosδi-l12sinδi)-2 Ωsinϕ(l12l23-l13l22)]·[2 Ωcosϕ(l12l21-l11l22)]-1;
Δωг1 д1i, Δωг1 д3i - модель разности двойного дрейфа в n положении и суммы дрейфов в i и j положениях соответственно до и после разворота гироскопа вокруг продольной оси объекта;
Δωг1 д2i, Δωг1 д4i - модель разности дрейфа в i и j положениях гироскопа соответственно до и после разворота гироскопа вокруг продольной оси объекта;
Δωг1 д1i=2[(ω1у 1у1g(c12cosδi+c22sinδi)-ω1у 1x1g(c22cosδi-c12sinδi)+ω1у 1y1z1·g2((c2 12-c2 22)cos2δi+2c12c22sin2δi)-ω1у 1у1у1g2(с12cosδi+c22sinδi)c32-ω1у 1z1z1g2(с12cosδi+c22sinδi)c32+ω1у 1x1y1g2(c22cosδi-c12sinδi)c32+2 ΩIY 1x1z1g2(0,5(c2 12-С2 22)sin2δi-c12c22cos2δi)];
Δωг1 д2i=2[(ω1у 1у1g(c12sinδi+c22cosδi)-ω1у 1x1g(c12cosδi+c22sinδi)-ω1у 1y1у1·g2((c12sinδi-c22cosδi)c32-ω1у 1z1z1g2(с12sinδi+c22cosδi)c32+ω1у 1x1у1g2(с12cosδi+c22sinδi)c32];
Δωг1 д3i=2[(ω1у 1у2g(m12cosδi+m22sinδi)-ω1у 1x2g(m22cosδi-m12sinδi)+ω1у 1y1z2·g2((m2 12-m2 22)cos2δi+2m12m22sin2δi)-ω1у 1у1у2g2(m12cosδi+m22sinδi)-ω1у 1z1z2g2(m12cosδi+m22sinδi)m32+ω1у 1x1y2g2(m22cosδi-m12sinδi)m32+2ωIY 1x1z2g2(0,5(m2 12-m2 22)sin2δi-m12m22cos2δi)];
Δωг1 д4i=2[(ω1у 1у2g(m12sinδi-m22cosδi)-ω1у 1x2g(m22cosδi+m22sinδi)-ω1у 1y1у2·g2((m12sinδi-m22cosδi)m32-ω1у 1у1z2g2(m12sinδi-m22cosδi)m32+ω1у 1x1y2g2(m12cosδi+m22sinδi)m32];
ω1у 1у1, ω1у 1у2 - коэффициенты модели дрейфа гироскопа от разбаланса вдоль оси собственного вращения соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1x1, ω1у 1х2 - коэффициенты модели дрейфа гироскопа от квадратурных моментов соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1y1z1, ω1у 1у1z2 - коэффициенты модели дрейфа гироскопа, пропорциональные ускорению во второй степени вдоль оси Yг1,
ω1у 1у1у1, ω1у 1z1z1; ω1у 1y1y2,ω1у 1z1z2 - коэффициенты модели дрейфа гироскопа от неравно-жесткости подвеса соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1x1у1, ω1у 1х1у2 - коэффициенты модели дрейфа гироскопа от перекрестного влияния при действии ускорений вдоль осей Xг1 и Zг1 гироскопа соответственно до и после его разворота вокруг продольной оси объекта;
ω1у 1х1z1, ω1у 1х1z2 - коэффициенты модели дрейфа гироскопа от перекрестного влияния при действии ускорений вдоль осей Xri и Yri гироскопа соответственно до и после его разворота вокруг продольной оси объекта;
υ,γ - углы наклона объекта соответственно по тангажу и крену;
μг1, αг1, βг1 -углы невыставки гироскопа на объекте;
е11=cosυsinβг1sinαг1+cosγsinυsinβг1cosαг1+sinγsinυcosβг1,
e12=cosγcosβг1-sinγsinβг1cosαг1,
e13=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1,
е21=cosυcosαг1-cosγsinυsinαг1,
е22=sinγsinαг1,
е23=sinυcosαг1+cosγcosυsinαг1,
l11=cosυsinβг1sinαг1-cosγsinυsinβг1cosαг1-sinγsinυcosβг1,
l12=-cosγcosβг1+sinγsinβг1cosαг1,
l13=sinυsinβг1sinαг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1,
l21=cosυcosαг1+cosγsinυsinαг1,
l22=-sinγsinαг1,
l23=sinυcosαг1-cosγcosυsinαг1,
C12=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1,
C22=sinυcosαг1+cosγcosυsinαг1,
С32=-sinυcosβг1sinαг1+cosγcosυcosβг1cosαг1-sinγcosυsinβг1,
m12=sinυsinβг1sinαг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1,
m22=sinυcosαг1-cosγcosυsinαг1,
m32=-sinυcosβг1sinαг1-cosγcosυcosβг1cosαг1+sinγcosυsinβг1,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта,
g - ускорение силы тяжести.
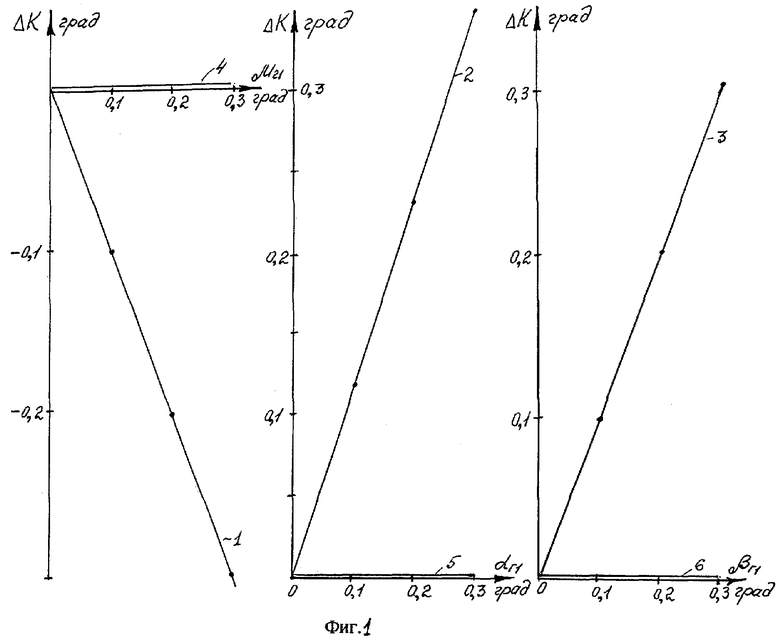
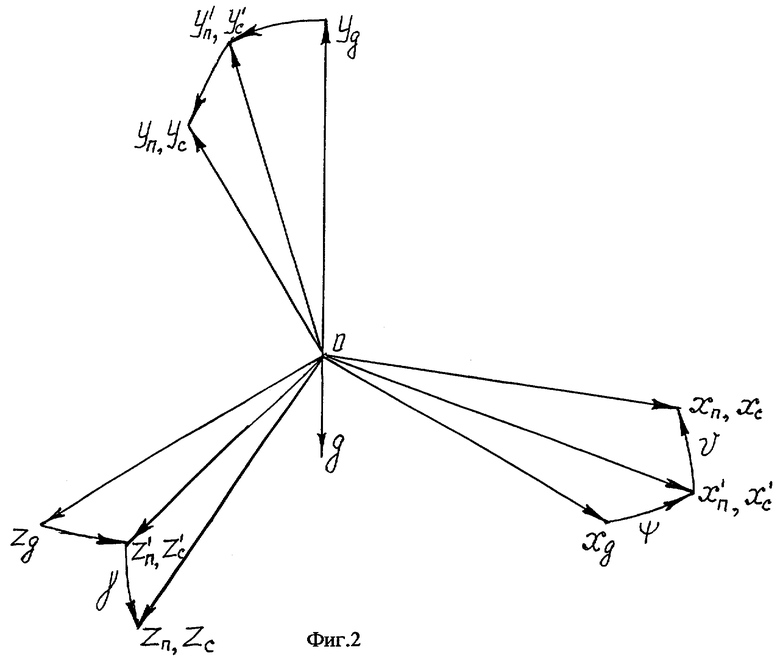
При анализе гирокомпасирования с применением предлагаемого способа используем следующие системы координат. Система координат ХдУдZд является географической: ось Хд направлена на север, ось Уд - вертикально вверх, ось Zд - на восток. С объектом свяжем систему координат XcYcZc: начало этой системы помещено в центр масс объекта, оси Хс и Ус расположены в вертикальной плоскости симметрии объекта, при этом ось Хс направлена вдоль оси корпуса объекта, а ось Ус - по перпендикуляру к оси Хс, лежащему в вертикальной плоскости симметрии объекта, ось Zc - перпендикулярна плоскости симметрии объекта и образует правую систему координат. Систему координат XпYпZп, свяжем с корпусом прибора. Систему координат Xг1Yг1Zг1 свяжем с гироскопом: оси Xг1 и Уг1 находятся в измерительной плоскости гироскопа, при этом ось Xг1 направлена по измерительной оси второго канала, а ось Уг1 по измерительной оси первого канала гироскопа, ось Zг1 направлена вдоль оси собственного вращения гироскопа. На фиг.2 показано взаимное расположение географической и связанных с объектом и корпусом прибора систем координат в первом исходном положении гироскопа. На фиг.3 показано взаимное расположение географической и связанных с объектом и корпусом прибора систем координат во втором исходном положении гироскопа. На фиг.4 показано взаимное расположение систем координат, связанных с корпусом прибора и гироскопом при неточной угловой выставке гироскопа.
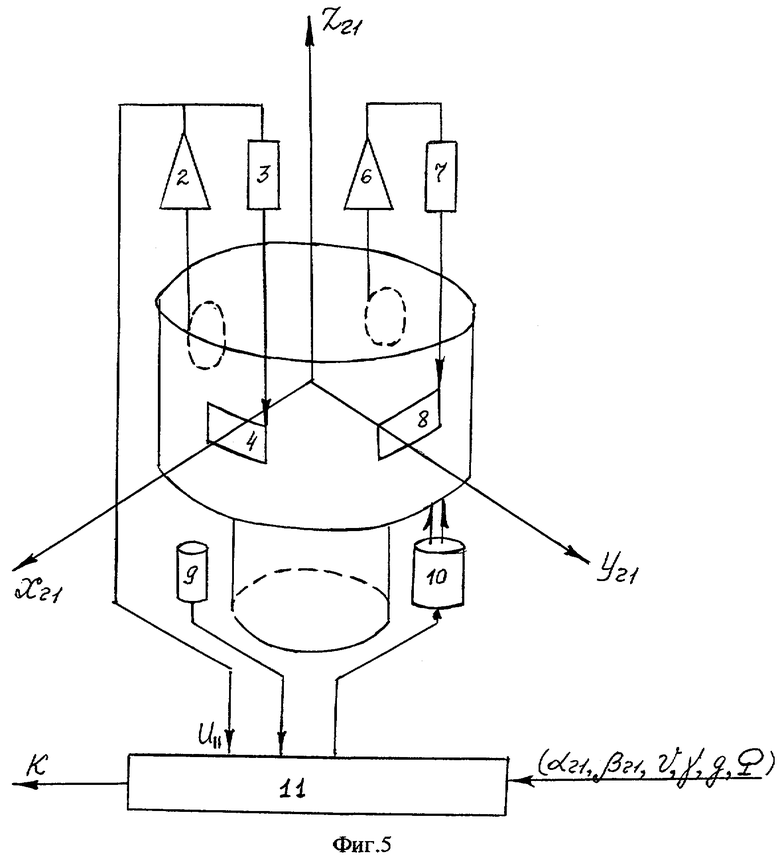
Схема гирокомпасирования с применением гироскопического датчика угловой скорости представлена на фиг.5. Гироскоп работает в режиме обратной связи по токам датчиков момента. Первый канал гироскопа содержит датчик угла 1, измеряющий поворот корпуса гироскопа относительно измерительной оси Уг1, усилитель 2, эталонное сопротивление 3, датчик момента 4, создающий момент вокруг оси Xг1. Второй, не используемый при гирокомпасировании канал содержит датчик угла 5, измеряющий поворот корпуса гироскопа относительно измерительной оси Xг1, усилитель 6, эталонное сопротивление 7, датчик момента 8, создающий момент вокруг оси Уг1. Показания гироскопа в виде напряжения U11, снимаемое с эталонного сопротивления по первому каналу, подается в вычислитель 11. В вычислитель также подается информация об углах наклона объекта по тангажу υ и крену γ, углах невыставки гироскопа относительно корпуса прибора αг1, βг1, широте местоположения объекта ϕ, значения угловой скорости вращения Земли и ускорения силы тяжести. Поворот гироскопа вокруг оси собственного вращения и измерение углов поворота осуществляется с помощью двигателя 10 и датчика угла 9. Гироскоп и устройства поворота гироскопа смонтированы в корпусе прибора.
Расположим гироскоп в первое исходное положение, как показано на фиг.2. В этом положении ось прибора Хп совпадает с осью объекта Хс, ось прибора Уп совпадает с осью объекта Ус, а ось прибора Zп - с осью объекта Zc. Пусть оси, связанные с объектом и прибором, наклонены на угол тангажа υ и угол крена γ. Положение осей координат, связанных с гироскопом и корпусом прибора, показано на фиг.4. Положим, что гироскоп неточно выставлен в корпусе прибора и имеет угловые ошибки невыставки μг1, αг1, βг1, как показано на фиг.4.
Пусть гироскоп обладает возможностью поворачиваться в диапазоне [0, 2π) радиан вокруг оси собственного вращения относительно корпуса прибора на углы δi против часовой стрелки, если смотреть с конца оси Zг1, где i - индекс, характеризующий положение гироскопа. Тогда показания гироскопа в i положении при условии малого угла невыставки μг1 можно представить в виде
U11i=(-Mx1i+H1ωг1 у1i)(H1Kн11)-1, (3)
где
ωг1 у1i - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа в 1 положении на δi угле,
ωг1 у1i=cosψ Ωcosϕ(e21cosδi-e11sinδi)+sinψ Ωcosϕ(е22созδi-e12sinδi)+ Ωsinϕ(e23cosδi-e13sinδi),
e11=cosυsinβг1sinαг1+cosγsinυsinβг1cosαг1+sinγsinυcosβг1;
e12=cosγcosβг1-sinγsinβг1cosαг1;
e13=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1;
e21=cosυcosαг1-cosγsinυsinαг1;
е22=sinγsinαг1;
е23=sinυcosαг1+cosγcosυsinαг1;
Mx1i=M1х 0i+M1x 1уig1уi+M1x 1xig1xi+М1x 1zig1zi+M1x 1у1zig2 1уi+М1x 1z1уig2 1zi+M1x 1y1yig1yig1уi+M1x 1z1zig1zig1уi+M1x 1x1уig1xig1zi+M1x 1x1zig1xig1уi,
g1xi, g1уi, g1zi - проекции ускорения силы тяжести g соответственно на оси Xг1, Уг1, Zг1 гироскопа в положении i,
g1xi=-g(C12cosδi+C22sinδi),
g1уi=g(C12sinδi-C22cosδi),
g1zi=-gC32,
C12=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1;
C22=sinυcosαг1+cosγcosυsinαг1;
С32=-sinυcosβг1sinαг1+cosγcosυcosβг1cosαг1-sinγcosυsinβг1;
М1х 0i - коэффициент модели вредного момента гироскопа, не зависящий от ускорения,
M1x 1yi - коэффициент модели вредного момента от разбаланса вдоль оси собственного вращения,
M1x 1xi - квадратурный коэффициент модели вредного момента,
M1x 1zi - коэффициент модели вредного момента, пропорциональный ускорению вдоль оси собственного вращения,
M1x 1y1zi - коэффициент модели вредного момента, пропорциональный второй степени ускорения вдоль оси Уг1,
M1x 1z1yi - коэффициент модели вредного момента, пропорциональный второй степени ускорения вдоль оси Zг1,
M1x 1y1yi, M1x 1z1zi - коэффициенты модели вредного момента от неравножесткости подвеса гироскопа,
M1x 1x1yi - коэффициент модели вредного момента от перекрестного влияния при действии ускорений вдоль осей Xг1 и Zг1,
M1x 1x1zi - коэффициент модели вредного момента от перекрестного влияния при действии ускорений вдоль осей Xг1 и Уг1,
H1 - кинетический момент гироскопа.
Практически при поворотах гироскопа на углы δi коэффициенты модели вредного момента мало отличаются друг от друга и этим отличием можно пренебречь. Положим, что при всех углах δi коэффициенты модели вредного момента сохраняют свои равные значения. Тогда, обозначив коэффициент индексом 1, выражение для модели вредного момента представим в виде
Mx1i=М1х 01+M1x 1ylg1yi+M1x 1x1g1xi+M1x 1z1g1zi+M1x 1y1z1g2 1zi+M1x 1y1y1g1yig1zi+M1x 1z1z1g1zig1yi+M1x 1x1y1g1xig1zi+M1x 1x1z1g1xig1yi, (4)
Повернем гироскоп вокруг оси собственного вращения из положения i в положение n=i+0,25N, угол между которыми составляет π/2 радиан.
Показания гироскопа в n положении можно представить в виде U11n=(-Mx1n+H1ωг1 y1n)H1Kн11)-1, (5)
где
ωг1 yn - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа в n положении,
ωг1 y1n=-cosψ Ωcosϕ(e21sinδi+e11cosδi)-sinψ Ωcosϕ(e22sinδi+e12cosδi)- Ωsinϕ(e23sinδi+e13cosδi),
g1xn, g1yn, g1zn - проекции ускорения силы тяжести соответственно на оси Хг1,Уг1, Zг1 гироскопа в положении n.
g1xn=-g(-C12sinδi+C22cosδi),
g1yn=g(C12cosδi+C22sinδi),
g1zn=-gC32,
Mx1n=M1x 01+M1x 1y1g1yn+M1x 1x1g1xn+M1x 1z1g1zn+М1x 1у1z1g2 1yn+M1x 1z1y1g2 1zn+M1x 1y1y1g1yng1zn+M1x 1z1z1g1zng1yn+M1x 1x1y1g1xng1zn+M1x 1x1z1g1xng1yn.
Повернем гироскоп вокруг оси собственного вращения из положения i в положение j=i+0,5N. Угол между этими положениями составляет π радиан.
Показания гироскопа в j положении можно представить в виде
U11j=(-Mx1j+H1ωг1 y1j)H1Kн11)-1,
где
ωг1 y1j - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа в j положении,
ωг1 у1j=-ωг1 y1i,
a1xj=-a1xi,
a1yj=-a1yi,
a1zj=a1zi,
Mx1j=M1x 01+M1x 1y1g1yj+M1x 1x1g1xj+M1x 1z1g1zj+М1x 1у1z1g2 1уj+M1x 1z1y1g2 1zj+M1x 1y1y1g1yjg1zj+M1x 1z1z1g1zjg1yj+M1x 1x1y1g1xjg1zj+M1x 1x1z1g1xjg1yj.
Вычтя из показаний гироскопа в i положении показания гироскопа в j положении, получим
U11i-U11j=[-(Mx1i-Mx1j)+H1(ωг1 y1i-ωг1 у1j)(H1Kн11)-1, (7)
где
Mx1i-Mx1j=2[M1x 1y1g(c12sinδi-c22cosδi)-M1x 1x1g(c12cosδi+c22sinδi)-M1x 1y1y1·g2(c12c32sinδi-c22c32cosδi)-M1x 1z1z1g2(c12c32sinδi-c22c32cosδi)],
ωг1 у1i-ωг1 y1j=2cosψ Ωcosϕ(e21cosδi-e11sinδi)+2sinψ Ωcosϕ(e22cosδi-e12sinδi)+2 Ωsinϕ(e23cosδi-e13sinδi).
Уравнение (7) можно представить в следующем виде:
где
Δωг1 д2i=(Mx1i-Мх1j)Н-1 1=2[ω1y 1y1g(c12sinδi-c22cosδi)-ω1У 1x1g(c12cosδi+c22sinδi)-ω1y 1y1y1·g2(c12sinδi-c22cosδi)c32-ω1y 1z1z1·g2(c12sinδi-c22cosδi)c32+ω1y 1x1y1g2(c12cosδi+c22sinδi)c32],
где
ω1y 1y1 - коэффициент модели дрейфа гироскопа от разбаланса вдоль оси собственного вращения в i положении,
ω1y 1x1 - коэффициент модели дрейфа гироскопа от квадратурного момента,
ω1y 1y1y1, ω1y 1z1z1 - коэффициенты модели дрейфа от неравножесткости подвеса,
ω1y 1x1y1 - коэффициент модели дрейфа гироскопа от перекрестного влияния при действии ускорений вдоль осей Xг1 и Zг1.
Вычитая из двойного показания гироскопа в положении n сумму показаний гироскопа в положениях i и j, получим
2U11n-(U11i+U11j)=[-(2Mx1n-Mx1i-Mx1j)+H1(2ωг1 yn-ωг1 yi-ωг1 yj)(H1Кн11)-1; (9)
где
2Mx1n-Mx1i-Mx1j=2[M1x 1y1g(c12cosδi+c22sinδi)-M1x 1x1g(c22cosδi-c12sinδi)+M1x 1y1z1·g2((c2 12-c2 22)cos2δi+2c12c22sin2δi)-M1x 1y1y1g2(c12cosδi+c22sinδi)c32-M1x 1z1zg2(c12cosδi+c22sinδi)c32+M1x 1x1y1g2(c22cosδi-c12sinδi)c32+2M1x 1x1z1·g2(0,5(c2 12-c2 22)sin2δi-c12c22cos2δi)],
2ωг1 y1n-ωг1 y1j-ωг1 y1j=-2[cosψ Ωcosϕ(e21sinδi+e11cosδi)+sinψ Ωcosϕ(е22sinδi+e12cosδi)+ Ωsinϕ(e23sinδi+e13cosδi)].
Уравнение (8) также можно представить в виде
cosψ[2 Ωcosϕ(e21sinδi+e11cosδi)]+sinψ[2 Ωcosϕ(е22sinδi+e12cosδi)]=(U11i+U11j-2U11n)Kн11-Δωг1 д1i-2 Ωsinϕ(e23sinδi+e13cosδi), (10)
где
Δωг1 д1i=(Mx1n-Мх1i-Mx1j)Н-1 1=2[ω1y 1y1g(c12cosδi+c22sinδi)-ω1y 1x1g(c22cosδi-c12sinδi)+ω1y 1y1y1g2((c2 12-c2 22)cos2δi+2c12c22sin2δi)-ω1y 1y1y1g2(c12cosδi+c22sinδi)c32-ω1y 1z1z1g2·(c12cosδi+c22sinδi)c32+ω1y 1x1y1g2(c22cosδi-c12sinδi)c32+2ω1y 1x1z1g2(0,5(c2 12-c2 22)sin2δi-c12c22cos2δi)],
ω1y 1z1z1 - коэффициент модели дрейфа гироскопа, пропорциональный ускорению во второй степени вдоль оси Уг1,
ω1y 1x1z1 - коэффициент модели дрейфа гироскопа от перекрестного влияния при ускорений вдоль осей Xг1 и Уг1,
Представим уравнение (7) и (9) в следующем виде:
a11icosψ+a12sinψ=b11i,
a21icosψ+a22isinψ=b12i, (11)
где
a11i=2 Ωcosϕ(e21cosδi-e11sinδi),
a12i=2 Ωcosϕ(e22cosδi-e12sinδi),
a21i=2 Ωcosϕ(e21sinδi+e11cosδi),
a22i=2 Ωcosϕ(e22sinδi+e12cosδi);
b11i=(U11i-U11j)Кн11+Δωг1 д2i-2 Ωsinϕ(e23cosδi-e13sinδi),
b12i=(U11i+U11j-2U11n)Kн11-Δωг1 д1i-2 Ωsinϕ(e23sinδi+e13cosδi).
Решая уравнение (11), можно определить выражения для sinψ и cosψ в следующем виде:
(sinψ)i=a1i,
(cosψ)i=b1i, (12)
где
a1i=[(U11i+U11j-2U11n)Kн11(e21cosδi-e11sinδi)-(U11i-U11j)Kн11(e21sinδi+e11cosδi)-Δωг1 д1i(e21cosδi-e11sinδi)-Δωг1 д2i(e21sinδi+e11cosδi)-2 Ωsinϕ(e13e21-e11e23)]·[2 Ωcosϕ(e12e21-е11е22)]-1,
b1i=[(U11i-U11j)Kн11(e22sinδi+e12cosδi)-(U11i+U11j-2U11n)Kн11(e22cosδi-e12sinδi)+Δωг1 д2i(e22sinδi+e12cosδi)+Δωг1 д1i(e22cosδi-e12sinδi)-2 Ωsinϕ(e12e23-e13e22)]·[2 Ωcosϕ(e12e21-e11e22)]-1.
Используя соотношение (12), искомый азимутальный угол ψi можно представить в следующем виде:
ψ1i=arctg(a1ib-1 1i) (13)
При использовании функции тангенса квадрант, в котором расположен азимутальный угол ψi, может быть вычислен по соотношению знаков для (sinψ)i и (cosψ)i в выражении (12).
Обозначив значение курса, определенное в первом положении при δi угле поворота корпуса гироскопа вокруг оси собственного вращения через К1i и зная квадрант, формулу для вычисления угла истинного курса, можно представить в виде
к1i=2π-arctg(a1ib-1 1i), если a1i>0, b1i>0;
к1i=π-arctg(a1ib-1 1i), если а1i>0, b1i<0;
к1i=π-arctg(а1ib-1 1i), если a1i<0, b1i<0;
к1i=-arctg(a1ib-1 1i), если a1i<0, b1i>0. (14)
Тогда осредненное по углу поворота гироскопа вокруг оси собственного вращения значение истинного курса в первом положении K1 получим в виде

Осреднение по углу поворота корпуса гироскопа вокруг оси собственного вращения гироскопа уменьшает погрешность гирокомпасирования от неучтенных факторов за счет того, что погрешность гирокомпасирования за оборот гироскопа меняет свой знак и ее среднее значение значительно меньше ее амплитудного значения.
Установим гироскоп во второе положение путем поворота его вместе с корпусом прибора вокруг продольной оси объекта на π радиан. Взаимное расположение географической и связанных с объектом, корпусом прибора систем координат во втором положении гироскопа показано на фиг.3. Исходная установка гироскопа во втором положении показана на фиг.4. При этой исходной установке оси гироскопа совпадают с осями корпуса прибора с точностью, обусловленной угловыми погрешностями установки μг1, αг1, βг1.
Так же, как и в первом положении, будем во втором положении гироскопа поворачивать его корпус в диапазоне [0, 2π) радиан вокруг оси собственного вращения относительно корпуса прибора на углы δi против часовой стрелки, если смотреть с конца оси Zг1.
Тогда показания гироскопа во втором положении при повороте на угол δi при условии малости углов невыставки μг1 можно представить в виде
U21i=(-Мх2i+H1ωг1 y2i)(H1Kн11)-1, (16)
где
ωг1 y2i - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа во втором положении на угле δi.
ωг1 y2i=cosψ Ωcosϕ(l21cosδi-l11sinδi)+sinψ Ωcosϕ(l22cosδi-l12sinδi)+ Ωsinϕ(l23cosδi-l13sinδi),
l11=cosυsinβг1sinαг1-cosγsinυsinβг1cosαг1-sinγsinυcosβг1;
l12=-cosγcosβг1+sinγsinβг1cosαг1;
l13=sinυsinβг1sinαг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1;
l21=cosυcosαг1+cosγsinυsinαг1;
l22=-sinγsinαг1;
l23=sinυcosαг1-cosγcosυsinαг1;
Mx2i - вредный момент по оси гироскопа Xг1 во втором положении на δi угле,
Mx2i=М1х 02i+M1 1y2ig1y2i+M1x 1x2ig1x2i+M1x 1z2ig1z2i+M1x 1y1z2i+M1x 1y1z2ig2 1y2i+M1x 1y1y2ig1y2ig1z2i+M1x 1z1z2ig1z2ig1z2i+M1x 1x1y2ig1x2ig1z2i+M1x 1x1z2ig1x2ig1y2i,
g1x2i, g1y2i, g1z2i - проекции ускорения силы тяжести g соответственно на оси Xг1, Уг1, Zг1 гироскопа во втором положении при повороте на угол δi,
g1x2i=-g(m12cosδi+m22sinδi),
g1y2i=g(m12sinδi-m22cosδi),
g1z2i=-gm32,
m12=sinυsinβг1sinβг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1;
m22=sinυcosαг1-cosγcosυsinαг1;
m32=-sinυcosβг1sinαг1-cosγcosυcosαг1cosαг1+sinγcosυsinβг1.
При переводе гироскопа из первого положения во второе возможно изменение коэффициентов модели вредного момента, поэтому эти коэффициенты обозначены цифрой 2 в отличие от первого положения, когда они были обозначены цифрой 1.
При поворотах на углы δi эти коэффициенты практически мало отличаются друг от друга и этим отличием можно пренебречь. Положим, что при всех углах δi коэффициенты модели вредного момента сохраняют свои значения и не зависят от угла δi. При этих условиях модель вредного момента представим в виде
Mx2i=М1х 02+M1х 1у2g1у2i+M1x 1x2g1x2i+M1х 1z2g1z2i+М1x 1z2g1z2i+M1x 1y1y2g1y2ig1z2i+M1x 1z1z2g1z2ig1y2i+M1x 1z2ig1x2ig1z2i+M1x 1x1z2g1x2ig1y2i.
Повернем гироскоп вокруг оси собственного вращения из положения δi в положение δn, где n=i+0,25N, и угол между которыми составляет π/2 радиан.
Показания гироскопа в положении δn можно представить в виде
U21n=(-Mx2n+H1ωг1 y2n)(H1Kн11)-1, (17)
где
ωг1 y2n - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа во втором положении на угле δn,
ωг1 y2n=-cosψ Ωcosϕ(l21sinδi+l11cosδi)-sinψ Ωcosϕ(l22sinδi+l12cosδi)- Ωsinϕ(l23sinδi+l13cosδi),
Mx2n=М1х 02+M1х 1у2g1у2n+M1x 1x2g1x2n+M1х 1z2g1z2n+М1x 1y1z2g2 1y2n+M1x 1z1y2g2 1z2n+M1x 1y1y2g1y2ng1z2n+M1x 1z1z2ig1z2ng1y2n+M1x 1x1y2g1x2ng1z2n+M1x 1x1z2g1x2ng1y2n,
g1x2n, g1y2n, g1z2n - проекции ускорения силы тяжести g соответственно на оси Хг1, Уг1, Zг1 гироскопа во втором положении на угле δn,
g1x2n=-g(-m12sinδi+m22cosδi),
g1y2n=g(m12cosδi+m22sinδi),
g1z2n=-gm32.
Повернем гироскоп вокруг оси собственного вращения из положения δi в положение j, где j=i+0,5N, и угол между этими положениями составляет π радиан.
Показания гироскопа при угле δj можно представить в виде
U21j=(-Mx2j+H1ωг1 y2j)(H1Kн11)-1, (18)
где
ωг1 y2j - проекция абсолютной угловой скорости на измерительную ось Уг1 первого канала гироскопа во втором положении на угле δj,
ωг1 y2j=-ωг1 у2i,
Mx2j=M1x 02+M1x 1y2g1y2j+M1x 1x2g1x2j+M1x 1z2g1z2j+M1x 1y1z2g2 1y2j+M1x 1z1y2g2 1z2j+M1x 1y1y2g1y2jg1z2j+M1x 1z1z2g1z2jg1y2j+M1x 1x1y2g1x2jg1z2j+M1x 1x1z2g1x2jg1y2j,
a1x2j=-a1x2i,
a1y2j=-a1y2i,
a1z2j=a1z2i.
Вычтем из показания гироскопа во втором положении на угле δi показания гироскопа на угле δj
U21i-U21j=[-(2Mx2i-Mx2j)+H1(ωг1 y2i-ωг1 y2j)(H1Kн11)-1, (19)
где
Mx2i-Mx2j=2[M1x 1y2g(m12sinδi-m22cosδi)-M1x 1x2g(c12cosδi+c22sinδi)-M1x 1y1y2g2(m12sinδi-m22cosδi)m32-M1x 1z1z2g2(m12sinδi-m22cosδi)m32],
ωг1 y2i-ωг1 y2j=2cosψ Ωcosϕ(l21cosδi-l11sinδi)+2sinψ Ωcosϕ(l22cosδi-l12Sinδi)+2 Ωsinϕ(l23cosδi-l13sinδi).
Уравнение (19) можно представить в виде
cosψ[2 Ωcosϕ(l21cosδi-l11sinδi)]+sinψ[2 Ωcosϕ(l22cosδi-l12sinδi)]=(U21i-U21j)Kн11+Δωг1 д4i-2 Ωsinϕ(l23cosδi-l13sinδi), (20)
где
Δωг1 д4i=(Мх1i-Mx1j)H1 -1=2[ω1y ly2g(m12sinδi-m22cosδi)-ω1y 1x2g(m12cosδi+m22sinδi)-ω1y 1y1y2g2(m12sinδi-m22cosδi)m32-ω1y 1z1z2g2(m12sinδi-m22cosδi)m32+ω1y 1x1y2g2(m12cosδi+m12sinδi)m32].
Вычтем из двойного показания гироскопа во втором положении на угле δn сумму показаний гироскопа на углах δi и δj.
2U21n-(U21i+U21j)=[-(2Mx2n-Mx2i-Mx2j)+Н1(2ωг1 y2n-ωг1 y2i-ωг1 y2j)-1; (21)
где
2Mx2n-Mx2i-Mx2j=2[M1x 1y2g(m12cosδi+m22sinδi)-M1x 1x2g(m22cosδi-m12sinδi)+M1x 1y1z2·g2((m2 12-m2 22)cos2δi+2m12m22sin2δi)-M1x 1y1y2g2(m12cosδi+m22sinδi)m32-M1x 1z1z2g2(m12cosδi+m22sinδi)m32+M1x 1x1y2g2(m22cosδi-m12sinδi)m32+2M1x 1x1z2·g2(0,5(m2 12-m2 22)sin2δi-m12m22cos2δi)],
2ωг1 y2n-ωг1 y2j-ωг1 y2j=-2[cosψ Ωcosϕ(l21sinδi+l11cosδi)+sinψ Ωcosϕ(l22sinδi+l12cosδi)+ Ωsinϕ(l23sinδi+l13cosδi)].
Уравнение (20) также можно представить в виде
где
Δωг1 д3i=(Мх2n-Mx2i-Mx2j)H1 -1=2[ω1y ly2g(m12cosδi+m22sinδi)-ω1y 1x2g(m22cosδI-m22sinδi)+ω1y 1y1z2g2(m2 12-m2 22)cos2δi+2m12m22sin2δi)-ω1y 1y1y2g2(m12cosδi+m22sinδi)m32-ω1y 1z1z2g2(m12cosδi+m22sinδi)m32+ω1y 1x1y2g2(m22cosδi-m12sinδi)m32+2ω1y 1x1z2g2(0,5(m2 12-m2 22)sin2δi-m12m22cos2δi)].
Представим уравнения (20) и (22) в следующем виде:
n11i(cosψ)i+n12i(sinψ)i=d11i,
n21i(cosψ)i+n22i(sinψ)i=b12i, (23)
где
n11i=2 Ωcosϕ(l21cosδi-l11sinδi),
n12i=2 Ωcosϕ(l22cosδi-l12sinδi),
n21i=2 Ωcosϕ(l21sinδi+l11cosδi),
n22i=2 Ωcosϕ(l22sinδi+l12cosδi);
d11i=(U21i-U21j)Kн11+Δωг1 д4i-2 Ωsinϕ(l23cosδi-l13sinδi),
d12i=(U21i+U21j-2U21n)Kн11-Δωг1 д3i-2 Ωsinϕ(l23sinδi+l13cosδi).
Решая уравнение (23), можно определить выражения для (sinψ)i и (cosψ)i в следующем виде:
(sinψ)i=а2i,
(cosψ)i=b2i, (24)
где
а2i=[(U21i+U21j-2U21n)Kн11(l21cosδi-l11sinδi)-(U21i-U21j)Kн11(l21sinδi+l11cosδi)-Δωг1 д3i(l21cosδi-l11sinδi)-Δωг1 д4i(l21sinδi+l11cosδi)-2 Ωsinϕ(l13l21-l11l23)]·[2 Ωcosϕ(l12l21-l11l22)]-1,
b2i=[(U21i-U21j)Kн11(l22sinδi+l12cosδi)-(U21i+U21j-2U21n)Kн11(l22cosδi-l12sinδi)+Δωг1 д4i(l22sinδi+l12cosδi)+Δωг1 д3i(l22cosδi-l12sinδi)-2 Ωsinϕ(l12l23-l13l22)]·[2 Ωcosϕ(l12l21-l11l22)]-1.
Используя соотношение (24), искомый азимутальный угол ψ2i можно представить в следующем виде:
ψ2i=arctg(a2ib-1 2i), (25)
а угол истинного курса K2i найти из следующих соотношений:
к2i=2π-arctg(a2ib-1 2i), если a2i>0, b2i>0;
к2i=π-arctg(a2ib-1 2i), если a2i>0, b2i<0;
к2i=π-arctg(a2ib-1 2i), если a2i<0, b2i<0;
к2i=-arctg(a2ib-1 2i), если a2i<0, b2i>0. (26)
Тогда осредненное по углу поворота гироскопа вокруг оси собственного вращения значение истинного курса во втором положении К2 можно представить в виде

Определим среднее значение курсового угла по результатам его измерения в первом и втором положении гироскопа.
Если разность между фактическим курсовым углом объекта и нулевым или 2π радиан значением курса не превышает азимутальной угловой невыставки гироскопа μг1, то для определения среднего значения курсового угла по его измерениям в двух положениях необходимо выполнить следующие дополнительные условия:
К1i=2π-arctg(a1ib-l 1i), если a1i<0, b1i>0, K1i<μ;
К1i=-arctg(a1ib-1 1i), если а1i<0, b1i>0, К1i>μ;
К2i=-arctg(a2ib-1 2i), если а2i<0, b2i>0, К2i>μ;
К2i=2π-arctg(a2ib-1 2i), если а2i<0, b2i>0, К2i<μ, (28)
где
μ - максимальная возможная величина азимутальной невыставки гироскопа.
Тогда с учетом условий (28) выражение для среднего значения курсового угла по измерениям в двух положениях можно представить в виде
К=0,5(K1+K2), если К<2π,
К=0,5(K1+K2)-2π, если К≥2π, (29)
где

к1i=2π-arctg(a1ib-1 1i), если a1i> 0, b1i>0;
к1i=π-arctg(a1ib-1 1i), если a1i>0, b1i<0;
к1i=π-arctg(a1ib-1 1i), если a1i<0, b1i<0;
к1i=-arctg(a1ib-1 1i), если a1i<0, b1i>0, К1i>μ;
к1i=2π-arctg(a1ib-1 1i), если a1i<0, b1i>0, К1i≤μ,
к2i=2π-arctg(a2ib-1 2i), если a2i>0, b2i>0;
к2i=π-arctg(a2ib-1 2i), если a2i>0, b2i<0;
к2i=π-arctg(a2ib-1 2i), если a2i<0, b2i<0;
к2i=-arctg(a2ib-1 2i), если а2i<0, b2i>0, K2i>μ;
к2i=2π-arctg(a2ib-1 2i), если a2i<0, b2i>0, К2i≤μ.
Как видно из соотношения (29) и представленных в (3) и (16) формул для е и 1, в предлагаемом способе проводится алгоритмическая компенсация погрешности гирокомпасирования от углов αг1 и βг1 невыставки гироскопа относительно корпуса прибора и объекта, характеризующих наклон гироскопа. Путем определения курсового угла по значениям курса, определенных в первом и втором положениях гироскопа, проводится автономная компенсация погрешности гирокомпасирования от угла μг1, характеризующего азимутальную невыставку гироскопа.
Рассмотрим как происходит автокомпенсация погрешности гирокомпасирования от азимутальной невыставки μг1 гироскопа на примере гирокомпасирования на горизонтальном объекте υ=γ=0, при точной выставке гироскопа в горизонт αг1 и βг1=0 и отсутствии дрейфа гироскопа Δωд1i=Δωг1 д2i=Δωг1 д3i=Δωг1 д4i=0.
Определим погрешность гирокомпасирования при установке гироскопа в первое положение. Погрешность гирокомпасировапия в этом случае можно представить в следующем виде:
Δψ1i=arctg[(a1icosψ-b1isinψ+(b1icosψ+a1isinψ)-1]. (30)
Для рассматриваемого случая в соответствии с (3) и (30)
e11=0, e12=1, e13=0, e21=1, e22=0, е23=0. (31)
Тогда в соответствии с (12) и (31)
a1i=[(U11i+U11j-2U11n)Kн11cosδi-(U11i-U11j)Kн11isinδi](2 Ωcosϕ)-1;
b1i=[(U11i-U11j)Kн11cosδi+(U11i+U11j-2U11n)Kн11sinδi](2 Ωcosϕ)-1. (32)
При нахождении показаний гироскопа необходимо учитывать угол его азимутальной невыставки μг1. Тогда с учетом его малости можно представить
e11=μг1, e12=1, e13=0, e21=1, e22=-μг1, e23=0. (33)
С учетом (7), (9) и (33) можно записать
U11i-U11j=2 Ωcosϕ[cosψ(cosδi-μг1sinδi)-sinψ(μг1cosδi+sinδi)K-1 н11;
U11i+U11j-2U11n=2 Ωcosϕ[cosψ(sinδi+μг1cosδi)+sinψ(cosδi-μг1sinδi)K-1 н11. (34)
Подставив (34) в (32), получим
a1i=μг1cosψ+sinψ,
b1i=cosψ-μг1sinψ. (35)
Подставив (35) в (30), получим следующую погрешность гирокомпасирования в первом положении:
Δψ1i=arctg{[(μг1cosψ+sinψ)cosψ-(cosψ-μг1sinψ)sinψ]·[{cosψ-μг1sinψ)cosψ+(μг1cosψ+sinψ)sinψ]-1. (36)
Выполнив в выражении (36) преобразования, получим
Δψ1i=arctgμг1=μг1. (37)
Определим погрешность гирокомпасирования при установке гироскопа во второе положение.
Погрешность гирокомпасирования для этого случая можно представить
Δψ2i=arctg[(a2icosψ-b2isinψ)(b2icosψ+a2isinψ)-1]; (38)
В этом положении в соответствии с (16)
l11=0, l12=-1, l13=0, l21=1, l22=-μг1, l23=0. (39)
Тогда в соответствии с (24) и (39)
a2i=-[(U21i+U21j-2U21n)Kн11cosδi-(U21i-U21j)Kн11sinδi](2 Ωcosϕ)-1;
b2i=[(U21i-U21j)Kн11cosδi+(U21i+U21j-2U21n)Kн11sinδi](2 Ωcosϕ)-1. (40)
При нахождении показаний гироскопа во втором положении также необходимо учитывать угол его азимутальной невыставки μг1. Тогда с учетом его малости можно представить
l11=μг1, l12=-1, l13=0, l11=1, l22=μг1, l23=0; (41)
Тогда согласно (19) и (21) с учетом (39) можно представить
U21i-U21j=2 Ωcosϕ[cosψ(cosδi-μг1sinδi)+sinψ(μг1cosδi+sinδi)]K-1 н11;
2U21n-U21i-U21j=-2 Ωcosϕ[cosψ(sinδi+μг1cosδi)+siniψ(μг1sinδi-cosδI)]K-1 н11. (42)
Подставив (42) в (40) и выполнив преобразования, получим
a2i=sinψ-μг1cosψ,
b2i=cosψ+μг1sinψ. (43)
Подставив (43) в (38), получим следующую погрешность гирокомпасирования во втором положении:
Δψ2i=arctg{[(sinψ-μг1cosψ)cosψ-(cosψ+μг1sinψ)sinψ)]·[(cosψ+μг1sinψ)cosψ+(sinψ-μг1cosψ)sinψ]-1}. (44)
Выполнив в выражении (44) преобразования, получим
Δψ1i=arctg(-μг1)=-μг1. (45)
Таким образом, определяя курсовой угол предлагаемым методом с помощью соотношения (29) как среднее значение курсовых углов в первом и втором положении гироскопа, получим согласно (37) и (45) нулевую погрешность гирокомпасирования от азимутальной невыставки μг1 гироскопа
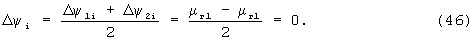
Таким образом, предлагаемый способ гирокомпасирования с применением гироскопического датчика угловой скорости при неточной выставке гироскопа на объекте имеет следующие отличия от известного способа:
- при операции гирокомпасирования вводится новое действие, связанное с определением углов наклона плоскости измерительных осей гироскопа относительно плоскости объекта, связанной с его продольной осью и осью, направленной к правому борту, что позволяет устранить погрешность гирокомпасирования от этой угловой невыставки гироскопа путем учета углов невыставки в аналитическом выражении для определения курсового угла,
- при операции гирокомпасирования вводится второе новое действие, связанное с поворотом гироскопа на π радиан вокруг продольной оси объекта, что позволяет выполнить автокомпенсацию погрешности гирокомпасирования, обусловленную азимутальной невыставкой гироскопа на объекте,
- определение истинного курсового угла производится по новым аналитическим зависимостям, определяющих курсовой угол как среднее значение курсовых углов в первом и втором положениях, учитывающих углы наклона объекта и использующих новую модель дрейфа гироскопа, что позволяет уменьшить влияние погрешности гирокомпасирования наклона объекта и угловых ошибок при выставке гироскопа на объекте.
На фиг.1 показаны зависимости погрешности гирокомпасирования от угловых ошибок установки гироскопа на горизонтальном объекте.
На фиг.2 представлено взаимное расположение географической и связанных с объектом и корпусом прибора систем координат в первом положении гироскопа.
На фиг.3 показано взаимное расположение географической и связанных с объектом корпусом прибора систем координат во втором положении гироскопа.
На фиг.4 представлено взаимное расположение систем координат, связанных с корпусом прибора и гироскопом при неточной угловой выставке гироскопа.
На фиг.5 показана схема гирокомпасирования с применением гироскопического датчика угловой скорости на основе динамически настраиваемого гироскопа при осреднении погрешности гирокомпасирования по углу поворота корпуса гироскопа вокруг оси собственного вращения.
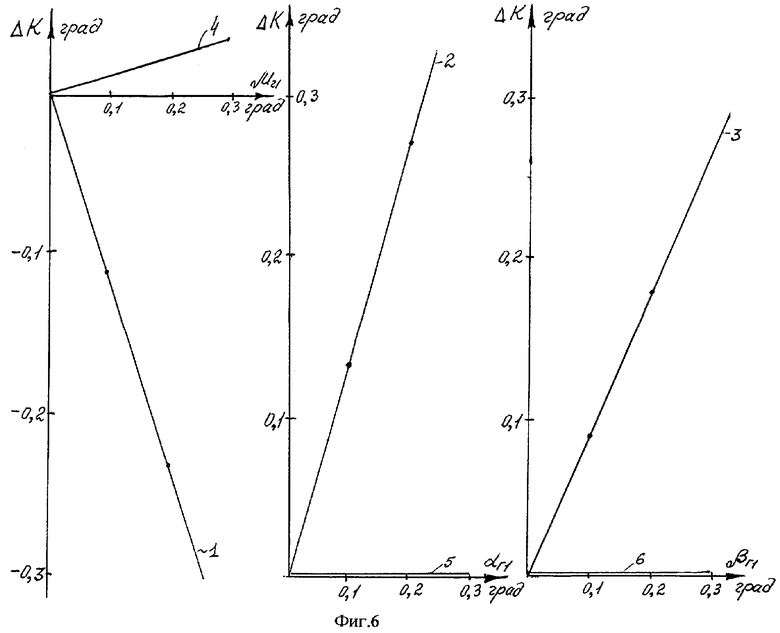
На фиг.6 представлены зависимости погрешностей гирокомпасирования от угловых ошибок установки гироскопа на наклонном объекте.
Проводились сравнительные теоретические исследования погрешностей гирокомпасирования, обусловленных угловыми ошибками выставки гироскопа на объекте с применением предлагаемого и известного способов. Выполнялись численные исследования с использованием предложенного аналитического выражения (29) и известного аналитического выражения (1). При расчете погрешностей использовались соотношения (30) и (38).
При числовом расчете погрешностей гирокомпасирования от ошибок угловой невыставки гироскопа использовались следующие параметры:
Ω=15 град/час, ϕ=55,5 град, Δϕ=0, Кн11=3,5·10-7 1/смв, ΔКн11=0;
ω1у 01=ω1у 02=1 град/час; ω1у 1x1=ω1у 1х2=1 град/час;
ω1у 1z1=ω1у 1z2=0,1 град/час; ω1у 1у1z1=ω1у 1у1y1z2=0,01 град/час;
ω1у 1у1у1=ωIY 1у1у2=0,05 град/час; ω1у 1z1z1=ω1у 1z1z2=0,05 град/час;
ω1у 1x1z1=ω1у 1x1z2=0,01 град/час; ω1у 1z1у1=ω1у 1z1у2=0,01 град/час;
ω1у 1у1=ω1у 1у2=1 град/час; ω1у 1x1у1=ω1у 1х1у2=0,01 град/час;
υ=γ=30 град.
На фиг.6 показаны зависимости погрешностей гирокомпасирования от угловых ошибок установки гироскопа на наклонном объекте. Зависимостями 1, 2, 3 показаны погрешности гирокомпасирования при использовании известного способа, а зависимостями 4, 5, 6 - погрешности гирокомпасироваиия с применением предлагаемого способа. Из сравнения этих зависимостей видно, что применение предлагаемого способа существенно уменьшает погрешности гирокомпасирования от ошибок угловой невыставки гироскопа на объекте.
Таким образом, использование предлагаемого способа позволяет существенно повысить точность гирокомпасирования при наличии углов наклона объекта по крену и тангажу, а также при неточной угловой выставке гироскопа на объекте.
Повышение точности гирокомпасирования расширяет область применения аналитических гирокомпасов с использованием датчика угловой скорости в геодезии, строительстве, авиации при начальной выставке по курсу бесплатформенных курсовертикалей и инерциальных систем.
Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании гирокомпасов аналитического типа. При гирокомпасировании с применением гироскопического датчика угловой скорости при неточной выставке гироскопа на объекте устанавливают гироскоп в первое исходное положение, при котором измерительная ось первого канала гироскопа совпадает с погрешностью установки с продольной осью объекта, измерительная ось второго канала гироскопа совпадает с погрешностью установки с осью объекта, направленной к правому борту, а ось собственного вращения гироскопа направлена с погрешностью установки по оси объекта, находящейся в плоскости его симметрии, определяют углы наклона плоскости измерительных осей гироскопа относительно плоскости объекта, связанной с его продольной осью и осью, направленной к правому борту, снимают показания с первого канала гироскопа на заданных углах поворота корпуса гироскопа вокруг оси собственного вращения, возвращают гироскоп в исходное положение, разворачивают корпус гироскопа вокруг продольной оси объекта на угол равный π радиан во второе положение и снимают показания с первого канала гироскопа на заданных углах поворота гироскопа вокруг оси собственного вращения, а затем находят угол истинного курса объекта как среднее значение курсовых углов, определенных в первом и втором положениях гироскопа с помощью аналитических выражений, использующих показания гироскопа, информацию об углах наклона объекта и углах наклона гироскопа относительно объекта, модель дрейфа гироскопа, широту местоположения объекта. 6 ил.
Способ гирокомпасирования с применением гироскопического датчика угловой скорости при неточной выставке гироскопа на объекте, включающий предварительную установку гироскопа в исходное положение, при котором измерительная ось Yг1 первого канала гироскопа совпадает с погрешностью установки с продольной осью объекта Хс, измерительная ось Xг1 второго канала гироскопа совпадает с погрешностью установки с направленной к правому борту объекта осью Zc, а ось собственного вращения гироскопа Zг1 направлена с погрешностью установки по оси объекта Yc, находящейся в плоскости его симметрии, работу гироскопа в режиме обратной связи по току датчика момента, фазировку сигнала с эталонного сопротивления с направлением поворота корпуса гироскопа вокруг оси собственного вращения, определение коэффициентов модели дрейфа гироскопа, а при гирокомпасировании определение углов наклона объекта по тангажу и крену, угла широты местоположения объекта, поворот корпуса гироскопа вокруг оси собственного вращения относительно исходного положения против часовой стрелки с измерением углов поворота корпуса гироскопа и напряжений с эталонного сопротивления первого канала, в равностоящих по углу друг от друга положениях, угловое расстояние между которыми выбирают таким, чтобы для него угол π/2 радиан являлся кратным, отличающийся тем, что при гирокомпасировании в первом исходном положении определяют углы наклона плоскости измерительных осей гироскопа относительно плоскости объекта, связанной с его продольной осью Хс и осью Zc, направленной к правому борту, потом снимают показания с первого канала гироскопа на заданных углах поворота корпуса гироскопа вокруг оси собственного вращения и возвращают гироскоп в исходное положение, после чего разворачивают корпус гироскопа вокруг продольной оси объекта на угол, равный π радиан, во второе положение и снимают показания с первого канала гироскопа на заданных углах поворота гироскопа вокруг оси собственного вращения, а затем находят угол истинного курса объекта по следующей формуле:
К=0,5(K1+К2) при К<2π;
К=0,5(K1+К2)-2π при К≥2π,
где K1, К2 - значения курсовых углов, осредненных по углу поворота гироскопа вокруг оси собственного вращения соответственно до и после разворота корпуса гироскопа вокруг продольной оси объекта;
i, j, n - текущие индексы, характеризующие положения гироскопа при его поворотах вокруг оси собственного вращения;
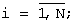
N=2πδ-1 - число измерений на интервале [0,2π)радиан;
δ=δi-1-δi - угол между i и i+1 положениями гироскопа;
j=i+0,5N при i≤0,5N;
j=i-0,5N при i>0,5N;
n=i+0,25N при i≤0,75N;
n=i-0,75N при i>0,75N;
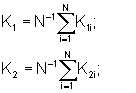
к1i=2π-arctg(a1ib-1 1i), если a1i>0, b1i>0;
к1i=π-arctg(а1ib-1 1i), если а1i>0, b1i<0;
к1i=π-arctg(a1ib-1 1i), если a1i<0, b1i<0;
к1i=-arctg(a1ib-1 1i), если a1i<0, b1i>0, K1i>μ;
к1i=2π-arctg(a1ib-1 1i), если а1i<0, b1i>0, K1i≤μ;
к2i=2π-arctg(a2ib-1 2i), если а2i>0, b2i>0;
к2i=π-arctg(a2ib-1 2i), если a2i>0, b2i<0;
к2i=π-arctg(a2ib-1 2i), если а2i<0, b2i<0;
к2i=-arctg(a2ib-1 2i), если a2i<0, b2i>0; K2i>μ;
к2i=2π-arctg(a2ib-1 2i), если а2i<0, b2i>0; K2i≤μ;
μ - максимально возможная величина азимутальной невыставки гироскопа;
a1i=[(U11i+U11j-2U11n)Kн11(e21cosδi-e11sinδi)-(U11i-U11j)Kн11(e21sinδi+е11cosδi-Δωг1 д1i·(e21cosδi-e11sinδi)-Δωг1 д2i(e21sinδi+e11cosδi)-2 Ωsinϕ(e13e21-е11е23)][2 Ωcosϕ(е12е21-e11e22)]-1;
b1i=[(U11i-U11j)Kн11(e22sinδi+e12cosδi)-(U11i+U11j-2U11n)Kн11(e22cosδi-е12sinδi)+Δωг1 д2i·(e22sinδi+e12cosδi)+Δωг1 д1i(e22cosδi+e12sinδi)-2 Ωsinϕ(e12e23-е13е22)][2 Ωcosϕ(е12е21-e11e22)]-1;
a2i=[(U21i+U21j-2U21n)Kн11(l21cosδi-l11sinδi)-(U21i-U21j)Kн11(l21sinδi+l11cosδi)-Δωг1 д3i(l21cosδi-l11sinδi)-Δωг1 д4i(l21sinδi+l11cosδi)-2 Ωsinϕ(l13l21-l11l23)]·[2 Ωcosϕ(l12l21-l11l22)]-1;
b2i=[(U21i-U21j)Kн11(l22sinδi+l12cosδi)-(U21i+U21j-2U21n)Kн11(l22cosδI-l12sinδi)+Δωг1 g4i·(l22sinδi+l12cosδi)+Δωг1 д3i(l22cosδi-l12sinδi)-2 Ωsinϕ(l12l23-l13l22)]·[2 Ωcosϕ(l12l21-l11l22)]-1;
Δωг1 д1i, Δωг1 д3i - модель разности двойного дрейфа в n положении и суммы дрейфов в i и j положениях соответственно до и после разворота гироскопа вокруг продольной оси объекта;
Δωг1 д2i, Δωг1 д4i - модель разности дрейфа в i и j положениях гироскопа соответственно до и после разворота гироскопа вокруг продольной оси объекта;
Δωг1 д1i=2[(ω1у 1у1g(c12cosδi+c22sinδi)-ω1у 1x1g(c22cosδi-c12sinδi)+ω1у 1y1z1·g2((c2 12-c2 22)cos2δi+2c12c22sin2δi)-ω1у 1у1у1g2(с12cosδi+c22sinδi)c32-ω1у 1z1z1g2(с12cosδi+c22sinδi)c32+ω1у 1x1y1g2(c22cosδi-c12sinδi)c32+2 ΩlY 1x1z1g2(0,5(c2 12-С2 22)sin2δi-c12c22cos2δi)];
Δωг1 д2i=2[(ω1у 1у1g(c12sinδi-c22cosδi)-ω1у 1x1g(c12cosδi+c22sinδi)-ω1у 1y1у1·g2((c12sinδi-c22cosδi)c32-ω1у 1z1z1g2(с12sinδi-c22cosδi)c32+ω1у 1x1у1g2(с12cosδi+c22sinδi)c32];
Δωг1 д3i=2[(ω1у 1у2g(m12cosδi+m22sinδi)-ω1у 1xzg(m22cosδi-m12sinδi)+ω1у 1y1z2·g2((m2 12-m2 22)cos2δi+2m12m22sin2δi)-ω1у 1у1у2g2(m12cosδi+m22sinδi)-ω1у 1z1z2g2(m12cosδi+m22sinδi)m32+ω1у 1x1y2g2(m22cosδi-m12sinδi)m32+2 Ω1у 1x1z2g2(0,5(m2 12-m2 22)sin2δi-m12m22cos2δi)];
Δωг1 д4i=2[(ω1у 1у2g(m12sinδi-m22cosδi)-ω1у 1x2g(m22cosδi+m22sinδi)-ω1у 1y1у2·g2((m12sinδi-m22cosδi)m32-ω1у 1у1z2g2(m12sinδi-m22cosδi)m32+ω1у 1z1z2g2(m12cosδi+m22sinδi)m32];
ω1у 1у1, ω1у 1у2 - коэффициенты модели дрейфа гироскопа от разбаланса вдоль оси собственного вращения соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1x1, ω1у 1х2 - коэффициенты модели дрейфа гироскопа от квадратурных моментов соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1y1z1, ω1у 1у1z2 - коэффициенты модели дрейфа гироскопа, пропорциональные ускорению во второй степени вдоль оси Yг1;
ω1у 1у1у1, ω1у 1z1z1, ω1у 1z1z2 - коэффициенты модели дрейфа гироскопа от неравножесткости подвеса соответственно до и после разворота гироскопа вокруг продольной оси объекта;
ω1у 1x1у1, ω1у 1х1у2 - коэффициенты модели дрейфа гироскопа от перекрестного влияния при действии ускорений вдоль осей Xг1 и Zг1 гироскопа соответственно до и после его разворота вокруг продольной оси объекта;
ω1у 1х1z1, ω1у 1х1z2 - коэффициенты модели дрейфа гироскопа от перекрестного влияния при действии ускорений вдоль осей Xг1 и Yг1 гироскопа соответственно до и после его разворота вокруг продольной оси объекта;
υ, γ - углы наклона объекта соответственно по тангажу и крену;
μг1, αг1, βг1 - углы невыставки гироскопа на объекте;
е11=cosυsinβг1sinαг1+cosγsinυsinβг1cosαг1+sinγsinυcosβг1,
e12=cosγcosβг1-sinγsinβг1cosαг1,
e13=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1,
е21=cosυcosαг1-cosγsinυsinαг1,
е22=sinγsinαг1,
е23=sinυcosαг1+cosγcosυsinαг1,
l11=cosυsinβг1sinαг1-cosγsinυsinβг1cosαг1-sinγsinυcosβг1,
l12=-cosγcosβг1+sinγsinβг1cosαг1,
l13=sinυsinβг1sinαг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1,
l21=cosυcosαг1+cosγsinυsinαг1,
l22=-sinγsinαг1,
l23=sinυcosαг1-cosγcosυsinαг1,
C12=sinυsinβг1sinαг1-cosγcosυsinβг1cosαг1-sinγcosυcosβг1,
C22=sinυcosαг1+cosγcosυsinαг1,
С32=-sinυcosβг1sinαг1+cosγcosυcosβг1cosαг1-sinγcosυsinβг1,
m12=sinυsinβг1sinαг1+cosγcosυsinβг1cosαг1+sinγcosυcosβг1,
m22=sinυcosαг1-cosγcosυsinαг1,
m32=-sinυcosβг1sinαг1-cosγcosυcosβг1cosαг1+sinγcosυsinβг1,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта;
g - ускорение силы тяжести.
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА С ПОМОЩЬЮ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 1995 |
|
RU2098766C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА НАКЛОННОГО ОБЪЕКТА С ПРИМЕНЕНИЕМ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 2001 |
|
RU2188392C1 |
| НАЗЕМНАЯ ГИРОСКОПИЧЕСКАЯ СИСТЕМА (ВАРИАНТЫ) | 2002 |
|
RU2213937C1 |
| WO 9904224 A1, 28.01.1999 | |||
| РАЗЪЕМНОЕ СОЕДИНЕНИЕ ТОНКОСТЕННЫХ ВОЗДУХОВОДОВ | 0 |
|
SU329344A1 |
Авторы
Даты
2006-01-10—Публикация
2004-07-08—Подача