Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании гирокомпасов аналитического типа.
Известны способы определения истинного курса с помощью гироскопического датчика угловой скорости (см., например, книгу Б.И.Назарова и Г.А.Хлебникова " Гиростабилизаторы ракет", М., 1975, стр.193-196 и патент RU 2098766 С1 по кл. G 01 С 21/14 от 10 декабря 1997 г.), согласно которым курсовое направление, горизонтально расположенной измерительной оси гироскопа на неподвижном основании, определяют аналитически с использованием показаний с гироскопа, полученных на разных азимутальных углах.
За прототип взят способ определения курса с помощью двухканального гироскопического датчика угловой скорости (см. патент RU 2176708 по кл. G 01 С 21/12 от 10 декабря 2001 г.).
В этом способе определения истинного курса с помощью двухканального гироскопического датчика угловой скорости предварительно привязывают измерительные оси гироскопа к осям, связанным с объектом, применяют гироскоп в режиме обратной связи по току датчика момента, определяют сигналы с эталонных сопротивлений датчика угловой скорости, проводят фазировку системы измерения напряжений с эталонных сопротивлений гироскопа, обеспечивающую отрицательное приращение сигналов с первого и второго каналов гироскопа при азимутальном повороте его корпуса против часовой стрелки на 90 градусов из положения, при котором измерительная ось Y первого канала направлена на север, а измерительная ось Х второго канала - на восток, определяют коэффициенты модели дрейфа гироскопа, а при гирокомпасировании в искомом курсовом положении объекта определяют углы наклона плоскости измерительных осей гироскопа по тангажу и крену, угол широты местоположения объекта, напряжения с эталонных сопротивлений гироскопа по первому и второму каналам, а затем определяют значение истинного курса измерительной оси первого канала гироскопа по следующей формуле:

где
а=b1b2 -1,
b1=-U11Кн11sinγsinυ-U12Кн12cosυ-ωг1 ДУsinγsinυ+ωг1 ДХcosυ+ Ωsinϕsinγ,
b2=U11Кн11cosγ+ωг1 ДУcosγ- Ωsinϕcosγsinυ,
ωг1 дх, ωг1 ду - модель дрейфа гироскопа по осям X, Y,
ωг1 дх=ω1х 0+ω1х 1хgsinγcosυ-ω1х 1ygsinυ-ω1х 1zgcosγcosυ+ω1x 1x1zg2sin2γcos2υ+ω1x 1z1xg2cos2γcos2υ-ω1x 1x1x0,5g2cos2υsin2γ-ω1x 1x1z0,5g2cos2υsin2γ-ω1x 1y1z0,5g2sinγsin2υ-ω1x 1y1x0,5g2cosγsin2υ,
ωг1 ду=ω1y 0+ω1y 1xgsinγcosυ-ω1y 1ygsinυ-ω1y 1zgcosγcosυ+ω1y 1y1zg2sin2υ+ω1y 1z1yg2cos2γcos2υ+ω1y 1y1y0,5g2cosγsin2υ+ω1y 1z1z0,5g2cosγsin2υ-ω1y 1x1y0,5g2cos2υsin2γ-ω1y 1x1z0,5g2sinγsin2υ,
ω0 1x, ω0 1y - коэффициенты модели дрейфа, не зависящие от ускорения,
ω1x 1x, ω1x 1y, ω1x 1z, ω1y 1x, ω1y 1y, ω1y 1z, ω1x 1z - коэффициенты модели дрейфа, пропорциональные ускорению в первой степени,
ω1x 1x1z, ω1x 1z1x, ω1x 1x1x, ω1x 1z1z, ω1x 1y1z, ω1x 1y1x, ω1y 1y1z, ω1y 1z1y, ω1y 1y1y, ω1y 1z1z, ω1y 1x1y, ω1y 1x1z - коэффициенты модели дрейфа, пропорциональные ускорению во второй степени,
Ui1, Ui2 - напряжения с эталонных сопротивлений датчиков угловой скорости соответственно по первому и второму каналам,
КH11, КH12 - крутизна гироскопа по напряжению для первого и второго каналов,
υ, γ - углы наклона плоскости осей чувствительности гироскопа соответственно по тангажу и крену,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта.
В известном способе производится аналитическая компенсация дрейфа гироскопа. Для этого дрейф гироскопа представляется в виде математической модели.
Составляющими этой модели являются:
- ω0 1x, ω0 1y - дрейф, не зависящий от ускорения,
- ω1x 1xg1x, ω1y 1yg1y - дрейф от разбаланса вдоль оси собственного вращения гироскопа Zг1,
- ω1x 1yg1y, ω1y 1xg1x - квадратурный дрейф,
- ω1x 1zg1z, ω1y 1zg1z - дрейф от ускорения вдоль оси собственного вращения гироскопа,
- ω1x 1x1zg2 1x, ω1y 1y1zg2 1y - дрейф от квадрата ускорения вдоль соответственно осей Хг1 и Yг1,
- ω1x 1z1xg2 1z, ω1y 1z1yg2 1z - дрейф от квадрата ускорения вдоль оси собственного вращения гироскопа,
- ω1x 1x1xg1xg1x, ω1x 1z1zg1z1x, ω1y 1y1yg1yg1z, ω1y 1z1zg1zg1y - дрейф от неравножесткости подвеса,
- ω1x 1y1xg1yg1z, ω1y 1x1yg1xg1z - дрейф от перекрестного влияния при действии ускорений g1x и g1z, g1y и g1z,
- ω1x 1y1zg1yg1x, ω1y 1x1zg1xg1y - дрейф от перекрестного влияния при действии ускорений g1x и g1y.
Для точной аналитической компенсации дрейфа необходимо точное знание коэффициентов модели дрейфа, которые определяются предварительно в результате калибровочных испытаний гироскопа. Однако эти коэффициенты являются нестабильными от запуска к запуску, а также изменяются в процессе временной наработки гироскопа. Наиболее сильно изменяются коэффициенты, обуславливающие:
- дрейф, не зависящий от ускорения,
- дрейф от разбаланса вдоль оси собственного вращения,
- квадратурный дрейф.
Имеется множество факторов, обуславливающих это изменение. Так, например, коэффициенты, вызывающие дрейф, не зависящий от ускорения, могут изменяться от изменения газодинамического момента вследствие изменения газовой среды прибора. Коэффициенты, обуславливающие дрейф от осевого разбаланса, могут изменяться от смещения центра масс ротора гироскопа вследствие температурной деформации сборки ротора гироскопа. Изменение коэффициентов квадратурного дрейфа может вызвать возникновение неперпендикулярности осей кручения торсионов к оси вала и несовпадение центров подвеса и масс. Изменение других коэффициентов модели дрейфа может быть обусловлено изменением коэффициентов податливости, характеризующих поступательное перемещение ротора гироскопа при приложении к нему в центре инерции сил вдоль осей подвеса, а также изменением параметров собственной вибрации гироскопа, обусловленной шарикоподшипниковой опорой, вследствие тепловых, силовых воздействий и временной наработки.
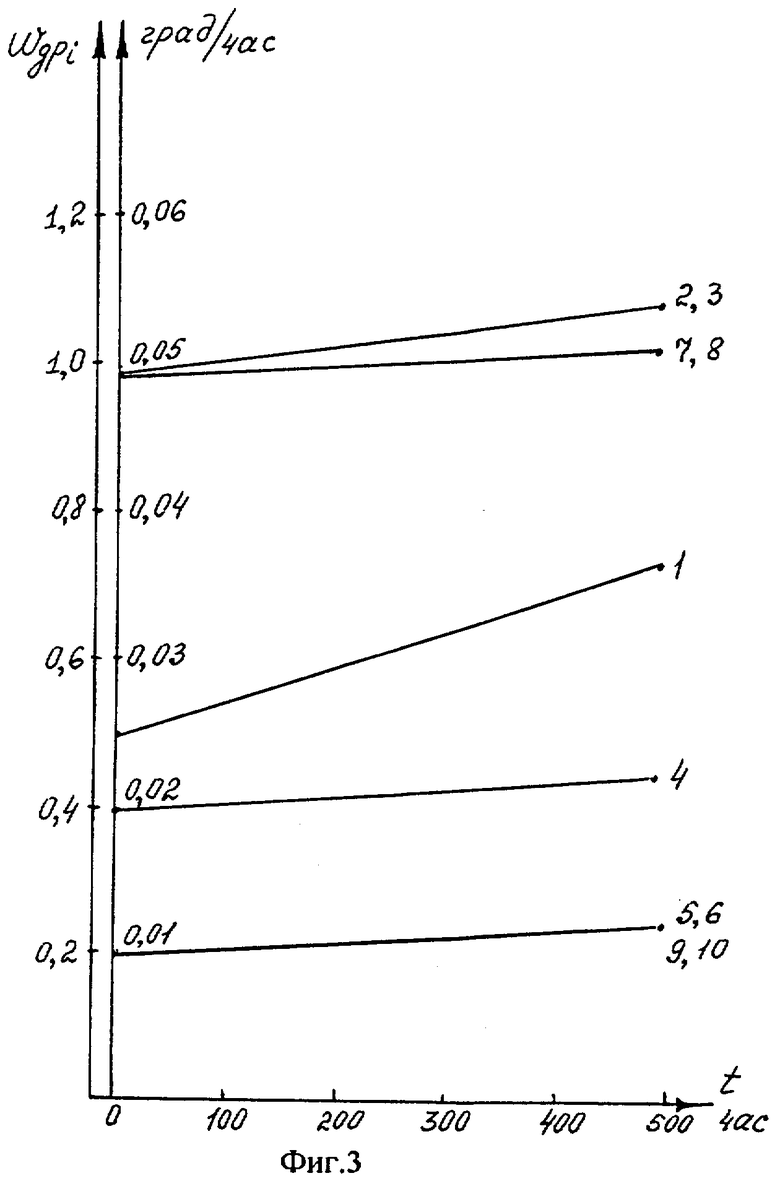
На фиг.3 показано типичное изменение составляющих дрейфа динамически настраиваемого гироскопа, вследствие изменения коэффициентов модели дрейфа в процессе временной наработки. Зависимостью 1 показан дрейф ω0 1x, ω0 1y, не зависящий от ускорения; зависимостями 2, 3 - дрейф ω1x 1xg1x, ω1y 1yg1y от разбаланса вдоль оси собственного вращения и ω1x 1yg1y, ω1y 1xg1x - квадратурный дрейф; зависимостью 4 - дрейф ω1x 1zg1z, ω1y 1zg1z от ускорения вдоль оси собственного вращения; зависимостями 5, 6 - дрейф ω1x 1x1zg2 1x, ω1y 1y1zg2 1y от квадрата ускорения вдоль соответственно осей Хг1 и Yг1, дрейф ω1x 1z1xg2 1z1, ω1y 1z1yg2 1z1 от квадрата ускорения вдоль оси собственного вращения; зависимостями 9, 10 - дрейф ω1x 1y1xg1yg1z, ω1y 1x1yg1zg1x от перекрестного влияния при действии ускорений g1x и g1z, g1y и g1z, дрейф ω1x 1y1zg1yg1x, ω1y 1x1zg1xg1y от перекрестного влияния при действии ускорений g1x и g1y, зависимостями 7, 8 - дрейф (ω1x 1x1x+ω1x 1z1z). g1xg1z, (ω1y 1y1y+ω1y 1z1z)g1z1g1y1 дрейф от неравножесткости подвеса.
На фиг.3 левая ось дрейфа относится к зависимостям 1, 2, 3, а правая - к остальным.
Погрешность гирокомпасирования, обусловленную изменением коэффициентов модели дрейфа, можно оценить с помощью следующего выражения:

где
Δb1, Δb2 - изменение величин b1, b2, подставленных в выражение (1), (2), вследствие неучтенного изменения дрейфа гироскопа.
Используя зависимости изменения составляющих дрейфа в процессе наработки гироскопа, показанных на фиг.3 с помощью выражения (2), проводился компьютерный расчет погрешностей гирокомпасирования при углах наклона υ=γ=30 град.
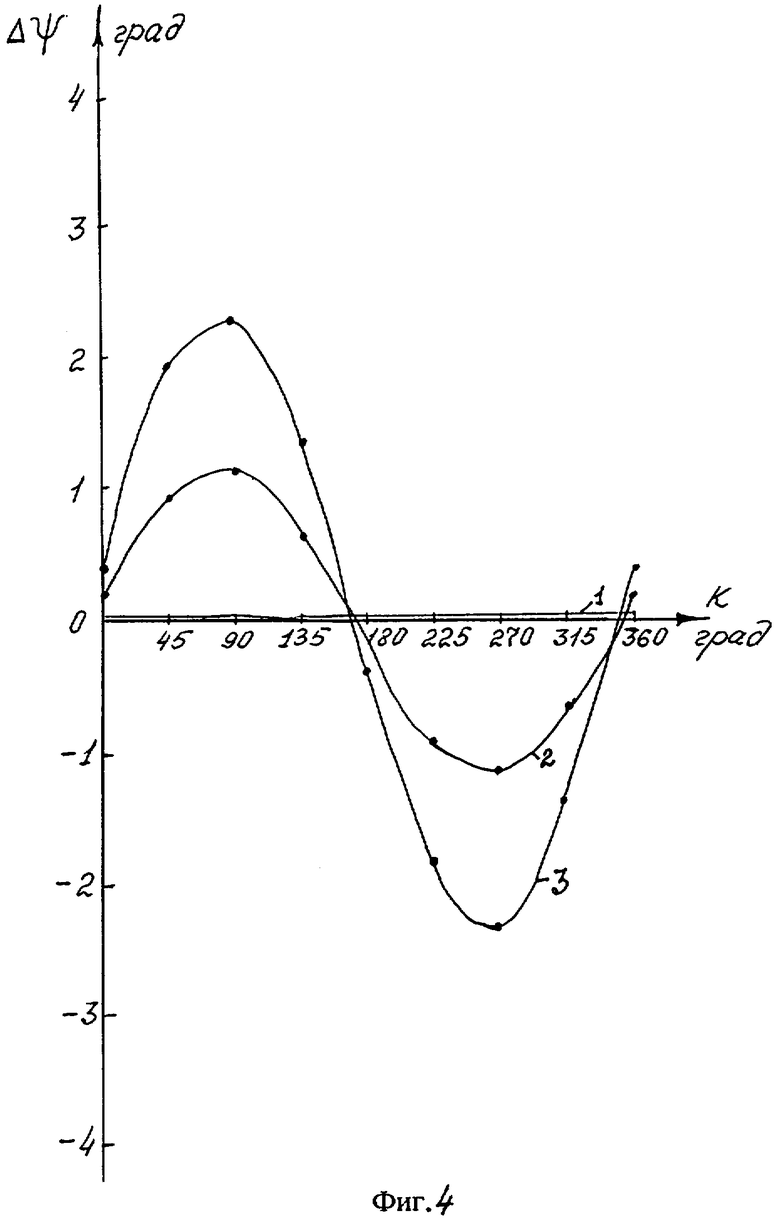
На фиг.4 показано изменение погрешностей гирокомпасирования на разных курсовых углах от изменения в процессе наработки коэффициентов модели дрейфа гироскопа при применении известного способа.
Зависимость 1 показывает погрешность в начальный момент, когда точно известны коэффициенты модели дрейфа, использующиеся при алгоритмической компенсации, зависимость 2 показывает погрешность гирокомпасирования после наработки 250 часов, а зависимость 3 - после наработки 500 часов.
Таким образом, проведенные числовые исследования показали, что при гирокомпасировании с применением известного способа изменение коэффициентов модели дрейфа приводят к существенным погрешностям гирокомпасирования.
Техническим результатом, который может быть получен при осуществлении настоящего изобретения, является повышение точности гирокомпасирования с применением гироскопического датчика угловой скорости.
Технический результат достигается тем, что в известном способе определения истинного курса с помощью двухканального гироскопического датчика угловой скорости, включающем работу гироскопа в режиме обратной связи по току датчика момента, предварительную фазировку сигналов с эталонных сопротивлений с направлением поворота корпуса гироскопа вокруг оси собственного вращения, а при гирокомпасировании определение углов наклона плоскости измерительных осей гироскопа по тангажу и крену, угла широты местоположения объекта, напряжений с эталонных сопротивлений гироскопа по первому и второму каналам, дополнительно при гирокомпасировании устанавливают гироскоп в первое исходное положение, при котором измерительная ось Yг1 первого канала гироскопа совпадает с продольной осью объекта Хс, измерительная ось Хг1 второго канала гироскопа совпадает с направленной к правому борту объекта осью Zс, а ось собственного вращения Zг1 направлена по оси объекта Yс, находящейся в плоскости его симметрии, и снимают показания с гироскопа в этом положении, потом устанавливают гироскоп во второе положение путем разворота его корпуса вокруг измерительной оси Yг1 на 180 градусов и снимают показания с гироскопа во втором положении, после этого переводят гироскоп из второго положения в третье в результате его разворота вокруг оси собственного вращения Zг1 на 180 градусов и снимают показания с гироскопа в третьем положении, а затем находят угол истинного курса объекта по следующей формуле:

где
a1=-(U121-U122)Кн12cosυ-(U111-U113)Кн11sinγsinυ+Δωг1 дх2cosυ-Δωг1 ду3sinγsinυ+2 Ωsinϕsinγ,
a2=(U111-U113)Кн11cosγ+Δωг1 ду3cosγ-2 Ωsinϕsinυcosγ,
Δωг1 дх2 - модель разности дрейфов в первом и втором положениях гироскопа по оси Хг1,
Δωг1 ду3 - модель разности дрейфов в первом и третьем положениях гироскопа по оси Yг1,
Δωг1 дх2=2(ω1x 1x1gsinγcosυ-ω1x 1z1gcosγcosυ+ω1x 1y1x1g2cosγsinυcosυ-ω1x 1y1z1g2sinγsinυcosυ),
Δωг1 дх3=-2(ω1y 1y1gsinυ+ω1y 1z1gcosγcosυ+ω1y 1x1y1g2sinγcosγcos2υ+
+ω1y 1x1z1g2sinγsinυcosυ);
ω1x 1x1, ω1y 1y1 - коэффициенты модели дрейфа гироскопа от разбаланса вдоль оси собственного вращения Zг1,
ω1x 1z1, ω1y 1z1 - коэффициенты модели дрейфа, пропорциональные ускорению вдоль оси собственного вращения,
ω1x 1y1x1, ω1y 1x1y1 - коэффициенты модели дрейфа от перекрестного влияния при действии ускорений по осям гироскопа Хг1 и Zг1, Yг1 и Zг1;
ω1x 1y1z1, ω1y 1x1z1 - коэффициенты модели дрейфа от перекрестного влияния при действии ускорения по осям Хг1 и Yг1,
U111, U121 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам в первом положении,
U112 и U122 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам во втором положении,
U113, U123 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам в третьем положении,
Кн11, Кн12 - коэффициенты крутизны гироскопа по напряжению соответственно по первому и второму каналам,
υ, γ - углы наклона плоскости осей чувствительности гироскопа соответственно по тангажу и крену,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта,
g - ускорение силы тяжести.
Схема гирокомпасирования с применением гироскопического датчика угловой скорости при бесплатформенной установке на объекте представлена на фиг.1.
При анализе этой схемы рассмотрим несколько систем координат.
Система координат ХдYдZд является географической: ось Хд направлена на север, ось Yд - вертикально вверх, ось Zд - на восток. С объектом свяжем систему координат ХсYс. Т.е. начало этой системы помещено в центр масс объекта, оси Хс и Yс расположены в вертикальной плоскости симметрии объекта, при этом ось Хс направлена вдоль оси корпуса объекта, а ось Yс - по перпендикуляру к оси Хс, лежащему в вертикальной плоскости симметрии объекта, ось Zс перпендикулярна плоскости симметрии объекта и образует правую систему координат. Систему координат Хг1Yг1Zг1 свяжем с гироскопом: оси Хг1 и Yг1 расположены в измерительной плоскости гироскопа, при этом ось Хг1 направлена по измерительной оси второго канала, а ось Yг1 - по измерительной оси первого канала гироскопа, ось Zг1 направлена вдоль оси собственного вращения гироскопа. Гироскоп работает в режиме обратной связи по токам датчиков момента и является двухканальным датчиком угловой скорости. Первый канал гироскопа содержит датчик угла 1, измеряющий поворот корпуса гироскопа относительно измерительной оси Yг1, усилитель 2, эталонное сопротивление 3, датчик момента 4, создающий момент вокруг оси Хг1. Второй капал содержит датчик угла 5, измеряющий поворот корпуса гироскопа относительно измерительной оси Хг1, усилитель 6, эталонное сопротивление 7, датчик момента 8, создающий момент вокруг оси Yг1. Показания гироскопа в виде напряжений U11 и U12, снимаемые с эталонных сопротивлении по первому и второму каналам, подаются в вычислитель 9.
В вычислитель также подается от других источников информация об углах наклона по тангажу υ и крену γ, о широте местонахождения объекта ϕ и значения об угловой скорости вращения Земли Ω и об ускорении силы тяжести g.
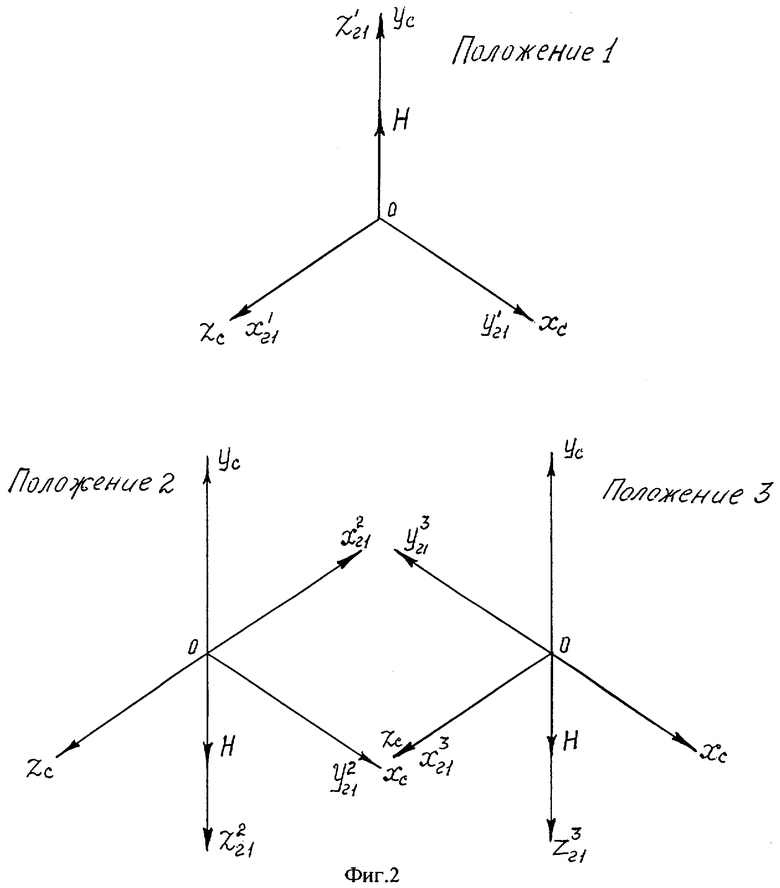
На фиг.2 показано расположение систем координат, связанных с объектом и гироскопом при гирокомпасировании.
Определим показания гироскопа в исходном положении 1, показанном на фиг.2. В положении 1 установим гироскоп таким образом, чтобы его измерительная ось Yг1 первого канала гироскопа совпадала с продольной осью объекта Хс, измерительная ось Хг1 второго канала гироскопа совпадала с направленной к правому борту объекта осью Zс, а ось собственного вращения Zг1 была направлена по оси объекта Yс, находящейся в плоскости его симметрии.
В установившемся режиме для изодромной обратной связи напряжения с эталонных сопротивлений датчика угловой скорости в первом положении можно представить в следующем виде:
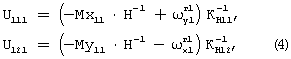
где
ωг1 x1=cosψcosϕ sinγsinυ+sinψ Ωcosϕ cosγ- Ωsinϕsinγcosυ,
ωг1 y1=cosψ Ωcosϕ cosυ+ Ωsinϕsinυ,
Мх11, My11 - вредные моменты, действующие по осям гироскопа Хг1, Yг1 в первом положении,
Мх11=М1x 01+М1x 1y1g1y1+М1x 1x1g1x1+М1x 1z1g1z1+М1x 1y1z1g2 1y1+М1x 1z1y1g2 1z1+М1x 1y1y1g1y1g1z1+М1x 1z1z1g1z1g1y1+М1x 1x1y1g1x1a1z1+М1x 1x1z1g1x1g1y1,
My11=М1y 01+М1y 1x1g1x1+М1y 1y1g1y1+М1y 1z1g1z1+М1y 1x1z1g2 1x1+М1y 1z1x1g2 1z1+М1y 1x1x1g1x1g1z1+М1y 1z1z1g1z1g1x1+М1y 1y1x1g1y1g1z1+М1y 1y1z1g1y1g1x1,
g1x1=gsinγcosυ,
g1y1=-gsinυ,
g1z1=-gcosγcosυ.
Определим показания гироскопа в положении 2, показанном на фиг.2. Во второе положение гироскоп переводится из первого положения путем разворота его корпуса вокруг измерительной оси Yг1 на 180 градусов.
Во втором положении показания гироскопа можно представить в следующем виде:
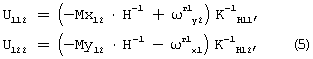
где
ωг1 x2=-ωг1 x1,
ωг1 y2=ωг1 y1.
Мх12, Му12 - вредные моменты, действующие по осям гироскопа Хг2, Yг2 в положении 2,
Мх12=М1x 02+М1x 1y2g1y2+М1x 1x2g1x2+М1x 1z2g1z2+М1x 1y1z2g2 1y2+М1x 1z1yzg2 1z2+М1x 1y1y2g1y2g1z2+М1x 1z1z2g1z2g1y2+М1х 1x1y2g1x2g1z2+М1x 1x1y2g1x2g1y2,
Му12=М1y 02+М1y 1x2g1x2+М1y 1y2g1y2+М1y 1z2g1z2+M1y 1x1z2g1x2+М1y 1z1x2g2 1z2+М1y 1x1x2g1x2g1z2+М1y 1z1z2g1z2g1x2+М1y 1y1x2g1y2g1z2+M1y 1y1z2g1y2g1x2,
g1x2=-g1x1,
g1y2=g1y1,
g1z2=-g1z1.
Определим показания гироскопа в положении 3, показанном на фиг.2. В третье положение гироскоп переводится из второго положения в результате его разворота вокруг оси собственного вращения Zг1 на 180 градусов.
В третьем положении показания гироскопа можно представить в следующем виде:
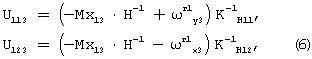
где
ωг1 x3=ωг1 x1,
ωг1 у3=-ωг1 у1,
Мх13, Му13 - вредные моменты, действующие по осям гироскопа XГ1, YГ1 в положении 3,
Мх13=М1x 03+М1x 1y3g1y3+М1x 1x3g1x3+М1x 1z3g1z3+М1x 1y1z3g2 1y3+М1x 1z1y3g2 1z3+М1x 1y1y3g1y3g1z3+М1x 1z1z3g1z3g1y3+М1х 1x1y3g1x3g1z3+М1x 1x1y3g1x3g1y3,
Му13=М1y 03+М1y 1x3g1x3+М1y 1y3g1y3+М1y 1z3g1z3+M1y 1x1z3g1x3+М1y 1z1x3g2 1z3+М1y 1x1x3g1x3g1z3+М1y 1z1z3g1z3g1x3+М1y 1y1x3g1y3g1z3+M1y 1y1z3g1y3g1x3,
g1x3=g1x1,
g1y3=-g1y1,
g1z3=-g1z1.
На практике изменение моментных коэффициентов при переводе в разные положения незначительно и ими можно пренебречь. Тогда, положим, что во всех положениях моментные коэффициенты сохраняют свои значения, которые они имели в первом положении.
Вычтем из показаний гироскопа по первому каналу в первом положении показания этого канала в третьем положении. Также вычтем из показаний по второму каналу в первом положении показания этого канала во втором положении. Тогда в соответствии с выражениями (4), (5), (6) получим
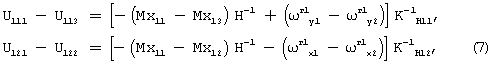
где
Мх11-Мх13=2(М1х 1y1g1y1+М1x 1z1g1z1+М1x 1x1y1g1x1g1z1+М1x 1x1z1g1x1g1z1),
Му11-Му13=2(М1y 1y1g1x1+М1y 1z1g1z1+М1y 1y1x1g1y1g1z1+М1x 1y1z1g1y1g1x1),
ωг1 y1-ωг1 y3=2ωг1 y1,
ωг1 x1-ωг1 x2=2ωг1 x1,
Учитывая, что ωУ=МхН1 -1, ωx=-МУН-1, уравнения (7) можно представить в следующем виде:
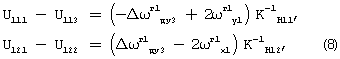
где
Δωг1 ду3=2(ω1y 1y1g1y1+ω1y 1z1g1z1+ω1y 1x1y1g1x1g1z1+ω1y 1x1z1g1x1g1y1),
Δωг1 дх2=2(ω1x 1x1g1x1+ω1x 1z1g1z1+ω1x 1y1x1g1y1g1x1+ω1x 1y1z1g1y1g1x1).
С учетом (4) уравнение (8) представим в виде
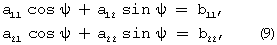
где
а11=2 Ωcosϕ·cosυ,
а12=0,
b11=(U111-U113)Кн11+Δωг1 ду3-2 Ωsinϕsinυ,
а21=2 Ωcosϕsinγsinυ,
а22=2 Ωcosϕcosγ,
b22=-(U121-U122)Кн12+Δωг1 ду3+2 Ωsinϕsinγcosυ.
Решая уравнение (9), определяем sinψ и cosψ и искомый азимутальный угол ψ в следующем виде:
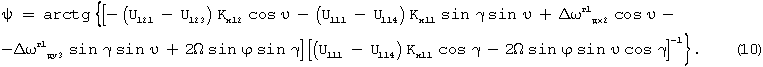
При использовании функции тангенса квадрант, в котором расположен азимутальный угол ψ, может быть вычислен по соотношению знаков числителя и знаменателя выражения (10). Зная квадрант, формулу для вычисления угла истинного курса можно представить в виде
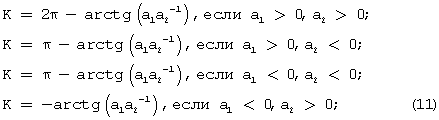
где
а1=-(U121-U122)Кн12cosυ-(U111-U113)Кн11sinγsinυ+Δωг1 дх2cosυ-Δωг1 ду3sinγsinυ+2 Ωsinϕsinγ,
а2=-(U111-U113)Кн11cosγ+Δωг1 ду3cosγ-2 Ωsinϕsinυcosγ.
Из полученного соотношения (10) для определения азимутального угла видно, что в его состав входят модели дрейфа по первому каналу Δωг1 ду3 и второму каналу Δωг1 дх2, определяемые соотношениями (8). Из соотношений (8) видно, что в предлагаемом способе дрейф гироскопа по первому и второму каналам имеет следующие составляющие:
- дрейф от осевого разбаланса,
- дрейф, пропорциональный ускорению вдоль оси собственного вращения,
- дрейф от перекрестного влияния при действии ускорений g1x и g1z, g1y и g1z,
- дрейф от перекрестного влияния при действии ускорений g1x и g1y.
В результате предлагаемого способа гирокомпасирования с использованием показаний гироскопа в его трех пространственных положениях удалось автономно скомпенсировать пять составляющих дрейфа, три из которых являются основоопределяющими составляющими дрейфа. Этими составляющими являются дрейф, не зависящий от ускорения, квадратурный дрейф, дрейф от неравножесткости подвеса. Оставшиеся не скомпенсированные автономным способом четыре составляющие дрейфа в предлагаемом способе компенсируются алгоритмически с использованием полученного соотношения (8).
Таким образом, предлагаемый способ гирокомпасирования с применением гироскопического датчика угловой скорости при автономной и алгоритмической компенсации его дрейфа имеет следующие отличия от известного способа:
- при операции гирокомпасирования вводятся два новых действия, связанных с изменением пространственной ориентации гироскопа относительно объекта путем перевода гироскопа из исходного положения в положение 2 в результате его разворота вокруг измерительной оси первого канала Yг1 и перевода гироскопа из положения 2 в положение 3 путем разворота гироскопа вокруг оси собственного вращения,
- при операции гирокомпасирования получено новое состояние по дрейфу гироскопа, связанное с автономной компенсацией значительной части составляющих его дрейфа в том числе дрейфа, не зависящего от ускорения, квадратурного дрейфа, дрейфа от неравножесткости,
- определение истинного курсового угла производится по новой аналитической зависимости, в которой введены новые разности показаний гироскопа в первом и втором положениях, первом и третьем положениях, используется новая модель дрейфа для алгоритмической компенсации, оставшейся после автономной компенсации составляющих дрейфа.
На фиг.1 представлена схема гирокомпрасирования с применением гироскопического датчика угловой скорости при бесплатформенной установке на объекте.
На фиг.2 показано расположение систем координат, связанных с объектом и гироскопом при гирокомпасировании.
На фиг.3 представлено типичное изменение составляющих дрейфа динамически настраиваемого гироскопа вследствие изменения коэффициентов модели дрейфа в процессе временной наработки.
На фиг.4 показано изменение погрешности гирокомпасирования на разных курсовых углах от изменения в процессе наработки коэффициентов модели дрейфа гироскопа при применении известного способа.
На фиг.5 представлено изменение погрешности гирокомпасирования на разных курсовых углах от изменения в процессе наработки коэффициентов модели дрейфа гироскопа при применении предлагаемого способа.
Проводились теоретические исследования точности гирокомпасирования с применением предлагаемого способа. Выполнялись численные исследования с использованием предложенного аналитического выражения (11). При расчетах погрешностей гирокомпасирования использовалось выражение (2), где вместо величин (b1+Δb1) и (b2+Δb2) брались величины (а1+Δа1) и (а2+Δа2), где Δа1 и Δа2 являются изменением значений а1 и а2 вследствие неучтенного изменения дрейфа гироскопа, возникающего в процессе временной наработки.
Используя зависимости изменения составляющих дрейфа в процессе наработки гироскопа, показанных на фиг.3, проводился компьютерный расчет погрешностей гирокомпасирования при углах наклона υ=γ=30 град.
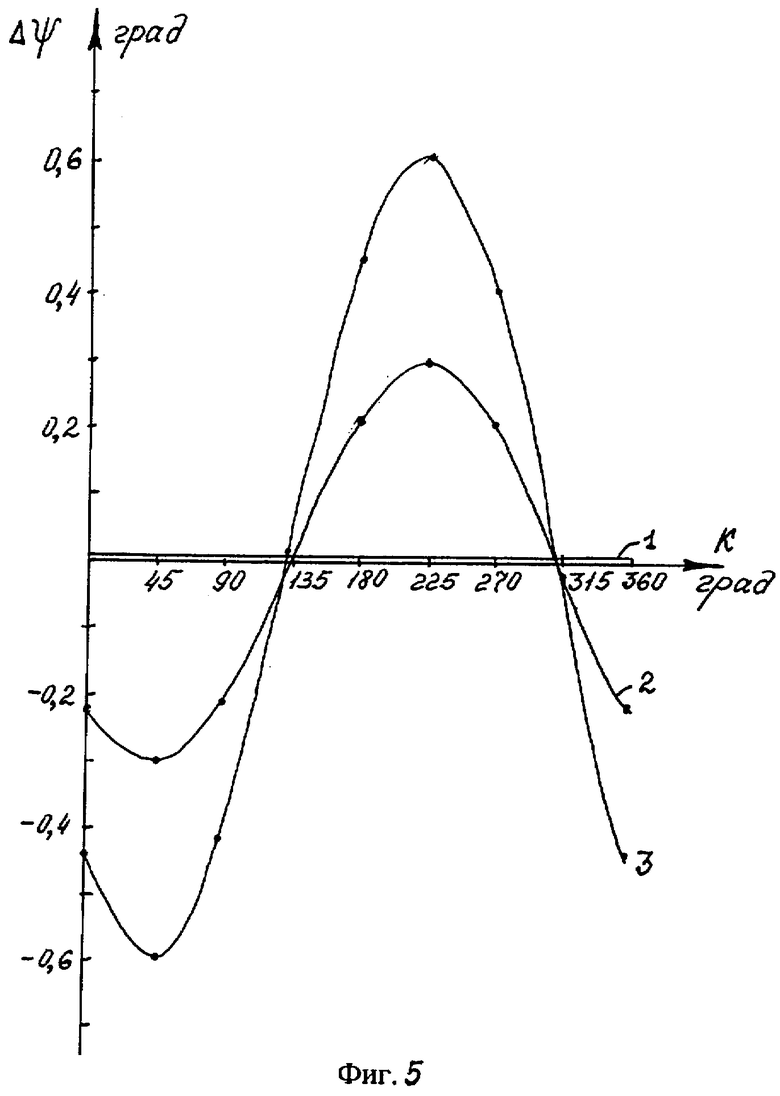
На фиг.5 показано изменение погрешностей гирокомпасирования на разных курсовых углах от изменения в процессе наработки коэффициентов модели оставшегося после автокомпенсации дрейфа гироскопа при применении предлагаемого способа. Зависимость 1 показывает погрешность в начальный момент. Зависимости 2 и 3 показывают погрешность гирокомпасирования соответственно после наработки 250 часов и 500 часов.
Из сравнения зависимостей, представленных на фиг.4 и фиг.5, видно, что при применении предлагаемого способа погрешность гирокомпасирования, обусловленная изменением в процессе временной наработки коэффициентов модели дрейфа гироскопа, значительно меньше в предлагаемом способе, чем в известном.
Таким образом, использование предлагаемого способа позволяет существенно повысить точность гирокомпасирования при наличии временной или от запуска к запуску нестабильности дрейфа гироскопа.
Повышение точности гирокомпасирования расширяет область применения аналитических гирокомпасов с применением датчика угловой скорости, например появляется возможность их использования в геодезии, строительстве, авиации при начальной выставке по курсу бесплатформенных курсовертикалей и инерциальных систем.
Изобретение относится к области точного приборостроения, преимущественно гироскопического, и может быть использовано при создании гирокомпасов аналитического типа. При гирокомпасировании с применением гироскопического датчика угловой скорости при автономной и алгоритмической компенсации его дрейфа устанавливают гироскоп в первое исходное положение, при котором измерительная ось первого канала гироскопа совпадает с продольной осью объекта, измерительная ось второго канала гироскопа совпадает с направленной к правому борту осью объекта, а ось собственного вращения гироскопа направлена по оси объекта, находящейся в плоскости его симметрии, и снимают показания с гироскопа в этом положении, потом устанавливают гироскоп во второе положение путем разворота его корпуса вокруг измерительной оси первого канала на 180° и снимают показания с гироскопа во втором положении, после этого переводят гироскоп из второго положения в третье в результате его разворота вокруг оси собственного вращения на 180° и снимают показания с гироскопа в третьем положении, а затем вычисляют угол истинного курса объекта с помощью аналитического выражения, используя информацию: о напряжениях с эталонных сопротивлений гироскопа в трех положениях и его остаточном после автокомпенсации дрейфе, об углах наклона плоскости осей чувствительности гироскопа по тангажу и крену, об угловой скорости вращения Земли, ускорении силы тяжести и широте местоположения объекта. 5 ил.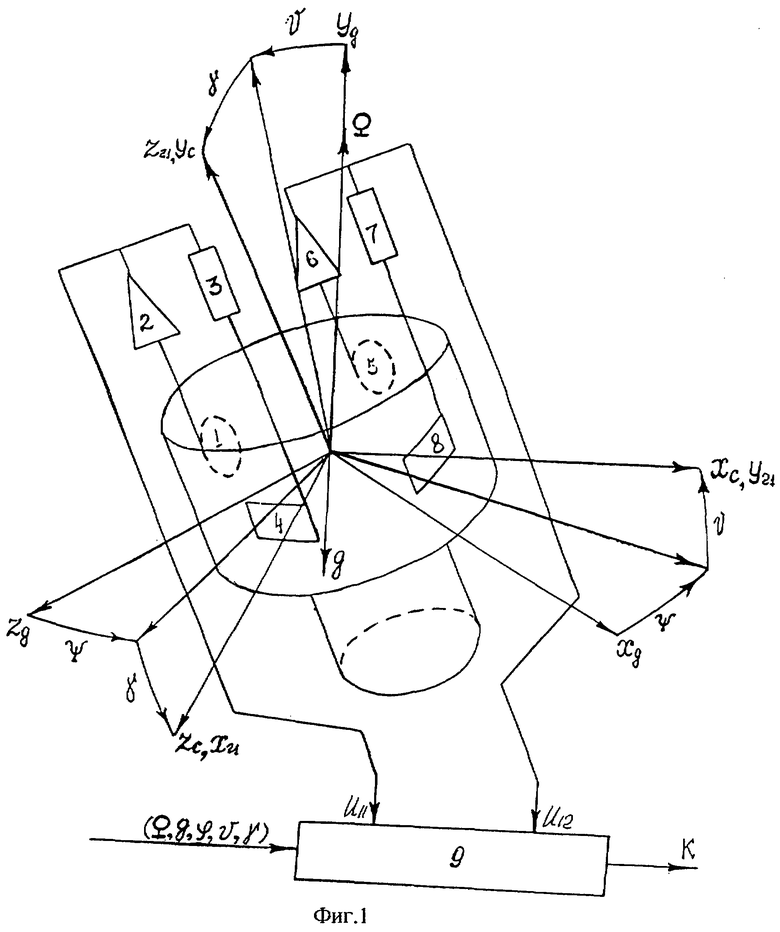
Способ гирокомпасирования с применением гироскопического датчика угловой скорости при автономной и алгоритмической компенсации его дрейфа, включающий предварительную привязку измерительных осей гироскопа к осям, связанным с объектом, работу гироскопа в режиме обратной связи по току датчика момента, предварительную фазировку сигналов с эталонных сопротивлений с направлением поворота корпуса гироскопа вокруг оси собственного вращения, а при гирокомпасировании определение углов наклона плоскости измерительных осей гироскопа по тангажу и крену, угла широты местоположения объекта, напряжений с эталонных сопротивлений гироскопа по первому и второму каналам, отличающийся тем, что при гирокомпасировании устанавливают гироскоп в первое исходное положение, при котором измерительная ось Уr1 первого канала гироскопа совпадает с продольной осью объекта Хс, измерительная ось Xr1 второго канала гироскопа совпадает с направленной к правому борту объекта осью Zc, а ось собственного вращения гироскопа Zr1 направлена по оси объекта Ус, находящейся в плоскости его симметрии, и снимают показания с гироскопа в этом положении, потом устанавливают гироскоп во второе положение путем разворота его корпуса вокруг измерительной оси Уr1 на 180° и снимают показания с гироскопа во втором положении, после этого переводят гироскоп из второго положения в третье в результате его разворота вокруг оси собственного вращения Zr1 на 180° и снимают показания с гироскопа в третьем положении, а затем находят угол истинного курса объекта по следующей формуле:
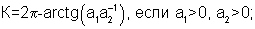
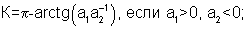
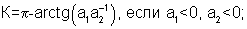
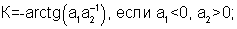
где
α1=-(U121-U122)Кн12cosυ-(U111-U113)Кн11sinγsinυ+Δωг1 дх2cosυ-Δωг1 ду3sinγsinυ+2 Ωsinϕsinγ,
α2=(U111-U113)Кн11cosγ+Δωг1 ду3cosγ-2 Ωsinϕsinυcosγ,
Δωг1 дх2 - модель разности дрейфов в первом и втором положениях гироскопа по оси Хг1,
Δωг1 ду3 - модель разности дрейфов в первом и третьем положениях гироскопа по оси Уг1,
Δωг1 дх2=2(ω1x 1x1gsinγcosυ-ω1x 1z1gcosγcosυ+ω1x 1y1x1g2cosγsinυcosυ-ω1x 1y1z1g2sinγsinυcosυ),
Δωг1 дх3=-2(ω1y 1y1gsinυ+ω1y 1z1gcosγcosυ+ω1y 1x1y1g2sinγcosγcos2υ+
+ω1y 1x1z1g2sinγsinυcosυ);
ω1x 1x1, ω1y 1y1 - коэффициенты модели дрейфа гироскопа от разбаланса вдоль оси собственного вращения Zг1,
ω1x 1z1, ω1y 1Z1 - коэффициенты модели дрейфа, пропорциональные ускорению вдоль оси собственного вращения,
ω1x 1y1x1, ω1y 1x1y1 - коэффициенты модели дрейфа от перекрестного влияния при действии ускорений по осям гироскопа Хг1 и Zг1, Уг1 и Zг1;
ω1x 1y1z1, ω1y 1x1z1 - коэффициенты модели дрейфа от перекрестного влияния при действии ускорения по осям Хг1 и Уг1,
U111, U121 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам в первом положении,
U112, U122 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам во втором положении,
U113, U123 - напряжения с эталонных сопротивлений гироскопа соответственно по первому и второму каналам в третьем положении,
Кн11, Кн12 - коэффициенты крутизны гироскопа по напряжению соответственно по первому и второму каналам,
υ, γ - углы наклона плоскости осей чувствительности гироскопа соответственно по тангажу и крену,
Ω - угловая скорость вращения Земли,
ϕ - широта местоположения объекта,
g - ускорение силы тяжести.
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА С ПОМОЩЬЮ ДВУХКАНАЛЬНОГО ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 2000 |
|
RU2176780C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА С ПОМОЩЬЮ ГИРОСКОПИЧЕСКОГО ДАТЧИКА УГЛОВОЙ СКОРОСТИ | 1995 |
|
RU2098766C1 |
| НАЗЕМНАЯ ГИРОСКОПИЧЕСКАЯ СИСТЕМА (ВАРИАНТЫ) | 2002 |
|
RU2213937C1 |
| JP 10246642 А, 14.09.1998 | |||
| РАЗЪЕМНОЕ СОЕДИНЕНИЕ ТОНКОСТЕННЫХ ВОЗДУХОВОДОВ | 0 |
|
SU329344A1 |
| WO 9904224 A1, 28.01.1999. | |||
Авторы
Даты
2006-03-20—Публикация
2004-07-08—Подача