Изобретение относится к области систем автоматического управления с эталонной моделью, а именно к управлению устойчивыми объектами с известными параметрами и структурой (дифференциальным уравнением).
Известен способ формирования сигнала управления с использованием сигнала задания и эталонного сигнала как реакции на сигнал задания [1] (прототип).
Недостатком известного способа является то, что сигнал задания системы управления и эталонная модель используются для формирования замкнутого управления, что может существенно влиять (уменьшать) на запасы устойчивости и увеличивать время переходного процесса, т.к. построение замкнутого управления осуществляется с использованием производных до (n-1)-гo порядка. Однако известно, что ошибки в формировании реальных производных выходного сигнала объекта управления тем выше, чем выше порядок «n» производной и амплитуды и частоты аддитивной помехи.
С целью повышения запасов устойчивости и уменьшения времени переходного процесса в системе управления любого порядка измеряют сигналы фазовых координат эталонного движения, усиливают их с соответствующими коэффициентами усиления, равными разности эталонных параметров и соответствующих параметров объекта управления, усиленные сигналы суммируют, дополнительно усиливают и используют полученный сигнал в качестве сигнала разомкнутого управления.
Рассмотрим для примера объект управления с известными параметрами (коэффициентами) дифференциального уравнения первого порядка:
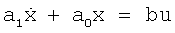
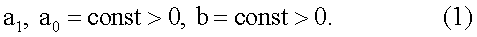
Требуется синтезировать такое управление u(t), чтобы выход объекта управления x(t) вел бы себя так же, как и выход эталонной модели xm(f), определяемый дифференциальным уравнением:
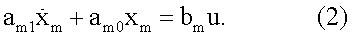
Решение задачи возможно, например, с помощью метода исключения старших производных или же с использованием только старших производных [1]. Оба метода предполагают необходимость определения производных, порядок которых не меньше «n-1», что на практике нереально осуществить точно.
Поэтому рассмотрим альтернативный подход к синтезу управления u(t). Будем называть этот метод методом эквивалентного дифференциального уравнения. С этой целью запишем эквивалентное уравнению (1) уравнение:
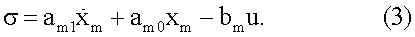
Если предположить, что x=xm, то записав из (1) эквивалентное уравнение
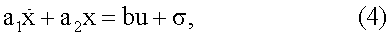
можем из (4) определить управление u(t), которое при подстановке найденного u(t) обратит уравнение (1) в уравнение (2):
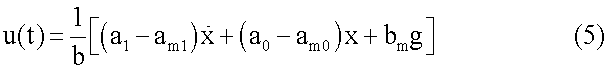
Очевидно, что при подстановке уравнения (5) в уравнение (1) получим уравнение эталонного движения (2), если x=xm.
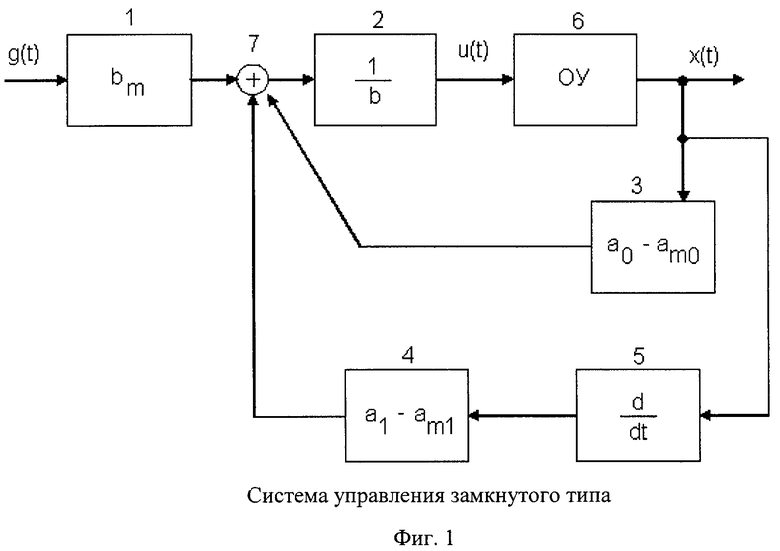
Суть изобретения иллюстрируется на фиг.1, фиг.2, фиг.3 и фиг.4.
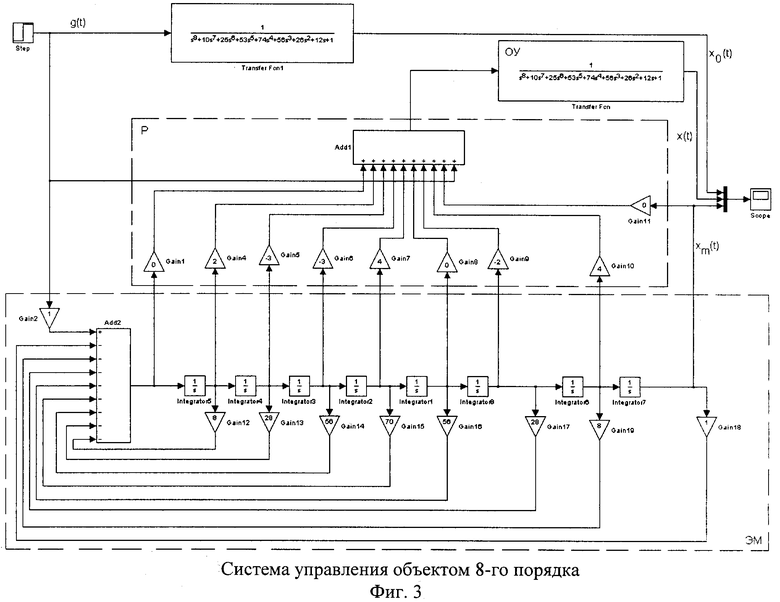
На фиг.1 представлена система управления замкнутого типа, на фиг.2 - разомкнутая система управления, на фиг.3 - система управления объектом восьмого порядка, на фиг.4 - переходные процессы на выходе объекта управления восьмого порядка, где приняты следующие обозначения: 1-4 - усилители, 5 - дифференциатор, 6 - объект управления, 7 - сумматор, 8-13 - усилители, 14, 15 - сумматоры, 16 - интегратор, 17 - объект управления. На фиг.3 приняты общепринятые в Simulink'e Matlab седьмой версии [2], x(t) - выход объекта управления, u(t) - сигнал управления, xm(t) - эталонный сигнал, g(t) - сигнал задания системы управления, Р - регулятор, ОУ - объект управления, ЭМ - эталонная модель.
Управление u(t) согласно (5) может быть реализовано в двух вариантах: в виде системы управления (включающей соединение регулятора Р, эталонной модели ЭМ и объекта управления ОУ) замкнутого типа, фиг.1, и разомкнутого типа, фиг.2. При этом вариант системы по фиг.1 требует определения старшей производной от выходного сигнала x(t) объекта управления. При объекте управления высокого порядка ошибка в определении старших производных на практике может быть велика. При наличии аддитивной помехи f(t) с уравнением объекта управления
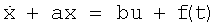 ,
,
высокочастотная составляющая f(t) «подчеркивается» дифференциаторами, это, как уже отмечалось, повышает вероятность потери устойчивости системы, уменьшения точности (повышение как динамической, так и статической ошибок) и ухудшения качества переходных процессов.
Реализация управления (5) в виде фиг.2 позволяет избавиться от действий помехи f(t) при формировании управления, т.к. f(t) на эталонную модель не действует. Сигналы производных любого порядка возможно непосредственно взять с выходов эталонной модели, в любую точку которой имеется доступ.
В этом случае необходимо точно знать структуру и параметры объекта управления. Кроме того, последний должен быть устойчивым. Чтобы расширить действие предложенного способа формирования управления на неустойчивые объекты, необходимо введение обратных связей с выхода объекта и затем осуществлять идентификацию параметров скорректированного уже устойчивого объекта.
Отметим, что реализация системы управления в виде фиг.2 имеет очень важное значение для практики использования систем управления.
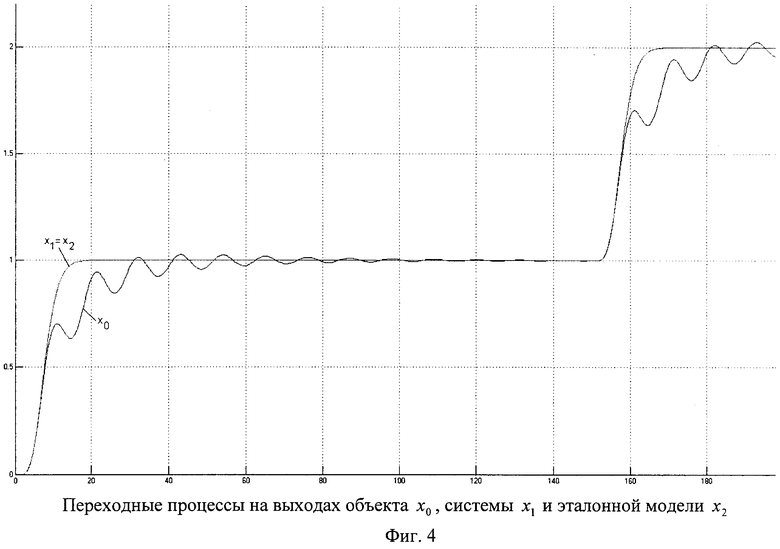
На фиг.3 представлена система управления объектом восьмого порядка, а на фиг.4 - переходные процессы в этой системе. Система управления фиг.3 построена в разомкнутом варианте с точным определением производных, получаемых на выходах эталонной модели. В этом случае в системе реализуются апериодические переходные процессы. При этом на фиг.4 реакции эталонной модели xm(t) и объекта управления x(t) на сигнал задания g(t) совпадают. Реакция же x0(t) объекта управления без регулятора значительно отличается от эталонной xm(t).
Заметим, что использование предложенного управления позволяет его выбрать всегда таким, чтобы задать в системе любое распределение корней системы управления [3]. Кроме того, достоинством системы фиг.2 является и то, что эталонную модель можно выбирать и на несколько порядков больше, чем порядок дифференциального уравнения объекта.
Реализация системы управления восьмого порядка по типу системы фиг.1 не позволяет обеспечить устойчивость и качество переходных процессов из-за неточности определения производных выходного сигнала x(t) объекта.
Изобретательский уровень предложенного способа управления подтверждается отличиями способа по сравнению с прототипом, отмеченными в формуле изобретения.
Источники информации
1. Бойчук Л.М. Метод структурного синтеза нелинейных систем автоматического управления. - М.: Энергия, 1971.
2. Черных И.В. Simulink: среда создания инженерных приложений / Под общей ред. В.Г.Потемкина. - М.: Диалог-МИФИ. 2003.
3. Кузовков Н.Т. Модальное управление и наблюдающие устройства. - М.: Машиностроение. 1976.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА НЕПРЯМОГО АДАПТИВНОГО УПРАВЛЕНИЯ | 2007 |
|
RU2381539C2 |
| СИСТЕМА ПРЯМОГО АДАПТИВНОГО УПРАВЛЕНИЯ | 2007 |
|
RU2367991C2 |
| СПОСОБ ФОРМИРОВАНИЯ АСТАТИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ ОБЪЕКТАМИ С НЕОПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ НА ОСНОВЕ ВСТРОЕННЫХ МОДЕЛЕЙ И МОДАЛЬНОЙ ИНВАРИАНТНОСТИ | 2014 |
|
RU2570127C1 |
| ДВУХКАНАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 2000 |
|
RU2171489C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ МНОГОМЕРНЫМ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ1^ГНЛ"ФОВД | 1972 |
|
SU429642A1 |
| САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА УПРАВЛЕНИЯ С ЭТАЛОННОЙ МОДЕЛЬЮ | 1990 |
|
RU2027211C1 |
| СПОСОБ САМОНАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ ОБЪЕКТОМ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2304298C2 |
| Способ формирования сигнала управления | 1979 |
|
SU857931A1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 1999 |
|
RU2150728C1 |
| Способ стабилизации положения плазменного шнура в токамаке | 1983 |
|
SU1119490A1 |
Изобретение может быть использовано для управления объектами с известными структурой и параметрами как линейными, так и нелинейными. Отличием предложенного способа формирования управления объектами с известными параметрами и структурой является то, что измеряют сигналы фазовых координат эталонного движения, усиливают их с соответствующими коэффициентами усиления, равными разности эталонных параметров и соответствующих параметров объекта управления, усиленные сигналы суммируют, дополнительно усиливают и используют полученный сигнал в качестве сигнала разомкнутого управления. Технический результат - повышение запасов устойчивости и уменьшение времени переходных процессов. 4 ил.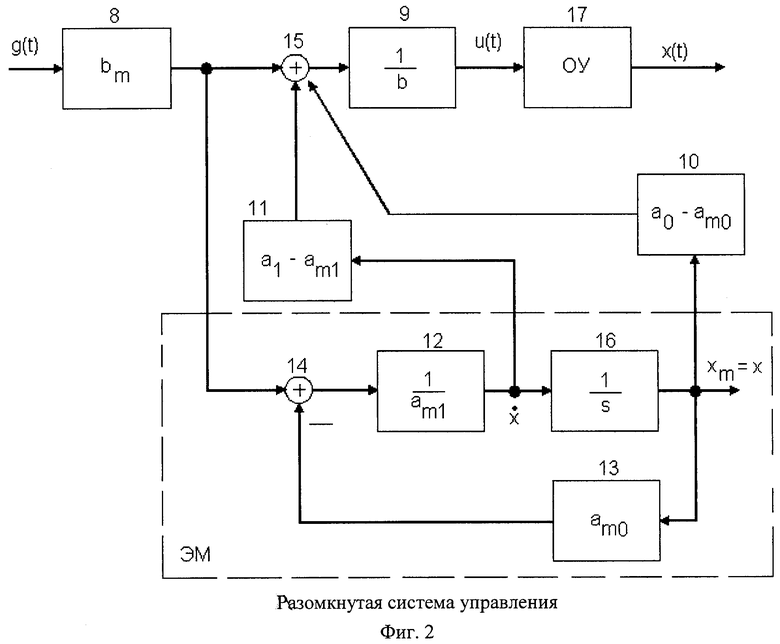
Способ формирования разомкнутого управления, заключающийся в том, что формируют усиленный сигнал задания и сигнал реакции эталонной модели, отличающийся тем, что с выходов эталонной модели снимают сигналы производных, усиливают их с коэффициентами усиления, равными разности коэффициентов усиления сигналов упомянутых производных и коэффициентов усиления сигналов производных от выходного сигнала объекта управления, причем порядки последних совпадают с соответствующими порядками производных, снятых с выходов эталонной модели, полученные усиленные сигналы суммируют с усиленным сигналом задания, дополнительно усиливают и используют полученный сигнал в качестве сигнала разомкнутого управления.
| СИСТЕМА АДАПТИВНОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМИ НЕЛИНЕЙНЫМИ ОБЪЕКТАМИ | 1990 |
|
RU2031434C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ГАЗОТУРБИННОГО ДВИГАТЕЛЯ | 2000 |
|
RU2172857C1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 1991 |
|
RU2039371C1 |
| Уточная вилочка для ткацких станков | 1933 |
|
SU37579A1 |
| US 2005149209 A1, 07.07.2005. | |||
Авторы
Даты
2010-08-10—Публикация
2007-08-28—Подача