Предлагаемый способ управления может быть использован в космической технике при сближении и последующей стыковке двух космических объектов, находящихся на околокруговой орбите небесного объекта, например пилотируемого космического корабля (ПКК), выводимого ракетоносителем (РН) в качестве активного космического объекта (АКО) и международной космической станцией (МКС) в качестве пассивного космического объекта (ПКО).
Известен способ управления, выбранный в качестве аналога, в котором для обеспечения сближения и последующей стыковки двух космических объектов АКО выводится в плоскость орбиты ПКО. Как правило, средняя высота орбиты ПКО находится выше средней высоты орбиты выведения АКО и поэтому после выведения АКО переводится на так называемую орбиту фазирования, находясь на которой осуществляется ликвидация начального углового рассогласования между двумя объектами. Это происходит вследствие того, что угловая скорость вращения вокруг небесного тела у АКО выше, чем у ПКО. После нескольких витков (число определяется выбранной баллистической схемой сближения) АКО с помощью двухимпульсного маневра переводится в окрестность ПКО, где сближение завершается автоматической стыковкой. Такой способ управления активным кораблем, применяемый при сближении и стыковке ПКК и грузовых кораблей (ГК) с МКС, требует выведения активного корабля в плоскость орбиты МКС [1]. При этом начальный фазовый угол между космическими объектами произволен, что требует определенного времени для его ликвидации, т.е. увеличения автономного полета АКО до стыковки. Это приводит к дополнительной нагрузке на экипаж ПКК, вынужденного продолжительное время находиться в стесненных условиях ограниченного объема космического корабля и практически совсем неприемлемо при реализации спасательной миссии на МКС, когда фактор времени сближения становится решающим.
Известен способ управления движением АКО, стыкующимся с ПКО за короткое время в течение одного витка, выбранный в качестве прототипа. Этот способ разработан для проведения сближения американского ПКК «Джемини-11» с третьей ступенью РН «Аджена». Используя выгодное расположение стартовой позиции космодрома на мысе Канаверал с районами падения первой и второй ступени РН, находящимися в Атлантическом океане, вначале выводился ПКО на восходящую часть витка орбиты с наклонением 28.84°. Затем, через виток, но уже на нисходящей части витка в плоскость орбиты ПКО выводился КК «Джемини-11» с заданным угловым рассогласованием между объектами в 12°, позволяющем завершить фазирование и оказаться в окрестности ПКО за один виток. Данный полет завершился успешной стыковкой ПКК «Джемини-11» со ступенью РН «Аджена» через 1 час 34 минуты после выведения, что на сегодняшний момент является лучшим результатом в пилотируемой космонавтике [2].
Основным недостатком такого способа управления является то, что его реализация возможна лишь при последовательном запуске ПКО и АКО на орбиту с фиксированным наклонением за определенное время для обеспечения необходимого начального фазового угла между объектами с большой точностью ±0.5°. В случае же со сближением и стыковкой с МКС или другим ПКО, уже находящемся на орбите, обеспечение необходимого начального фазового угла потребует от ПКО проведения многочисленных коррекций в течение нескольких месяцев перед стартом АКО для формирования орбиты стыковки с необходимой точностью. Учитывая напряженный график полетов пилотируемых кораблей к МКС (так, только в 2010 году 4 полета ПКК «Союз-ТМА» и 5 полетов «Спейс Шаттл») [3], и массу МКС (более 340 тонн), это потребует дополнительно большого количества топлива на проведение маневров. Резервная дата старта АКО при формировании фазового диапазона ±0.5° практически нереализуема. В случае же проведения миссии корабля-спасателя подготовка условий для быстрого сближения потребует слишком много времени, несопоставимого с временем полета к ПКО [4].
Техническим результатом изобретения является сокращение продолжительности сближения с ПКО, находящемся на орбите длительное время, при сохранении приемлемой частоты дат старта АКО без проведения дополнительных коррекций на ПКО. При этом, в зависимости от энергетики РН, частота запусков на орбиту для проведения сближения и стыковки может быть обеспечена в каждые сутки, что существенно лучше существующей двухсуточной схемы сближения, обеспечивающей частоту 1 раз в двое суток.
Технический результат достигается благодаря тому, что в способе управления движением активного космического объекта, стыкуемого с пассивным космическим объектом, включающем выведение активного космического объекта на целевую орбиту, в отличие от известного производят выведение активного космического объекта на целевую орбиту с отклонением несовпадающую по долготе восходящего узла орбиты с орбитой пассивного космического объекта на величину ΔλВУ, но с заданным рассогласованием по аргументу широты ΔФ, после чего, в перпендикулярном направлении к плоскости выведения, выполняют первый маневр в угловом интервале Δφ1 от точки выведения на целевую орбиту для изменения долготы восходящего узла орбиты на ΔλВУ1 за счет формирования импульса ΔV1, а затем в противоположном направлении в угловом интервале Δφ2 выполняют второй маневр с дросселированием тяги двигателя активного космического объекта для ликвидации рассогласования по наклонению целевой орбиты Δi1, возникшему после первого маневра и созданию дополнительного отклонения по долготе восходящего узла ΔλВУ2 за счет формирования импульса ΔV2, приводящего к совпадению плоскостей орбит стыкуемых объектов.
Технический результат в предлагаемом способе управления достигается тем, что время выведения АКО на орбиту выбирается таким образом, чтобы в момент выведения разница в аргументах широты АКО и ПКО ΔФ была равна заданной.
Сущность изобретения поясняется фиг.1÷7 и табл.1 и 2.
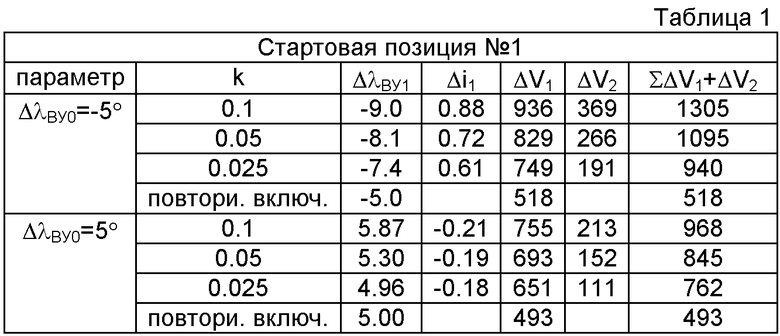
На фиг.1 показана схема сближения КК «Союз-ТМА» с МКС,
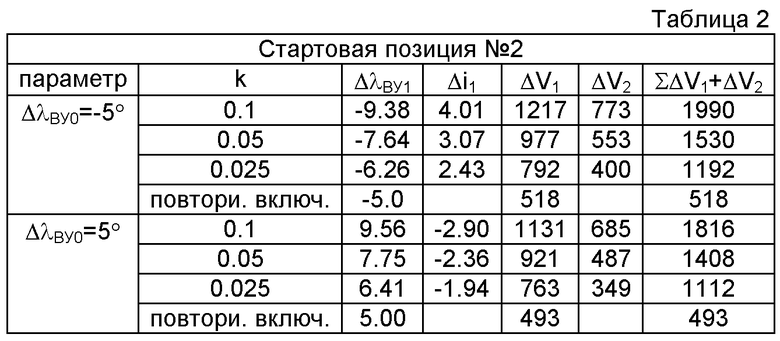
на фиг.2 представлены орбитальные элементы и направления маневров,
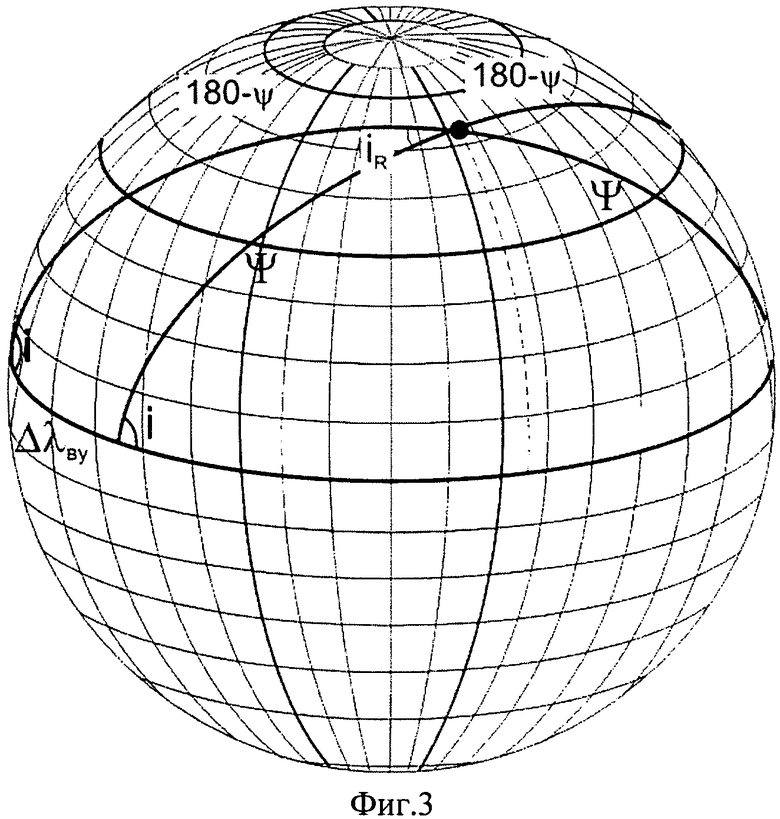
фиг.3 представляет взаимное положение двух орбит с одинаковым наклонением, отличающихся по положению восходящего узла орбиты,
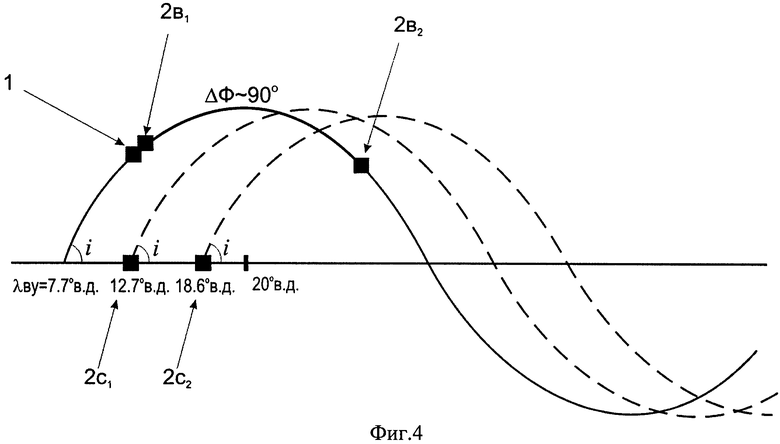
фиг.4 иллюстрирует зависимость значения начального фазового угла в момент выведения АКО от положения долготы восходящего узла орбиты ПКО в момент его прохождения экватора,
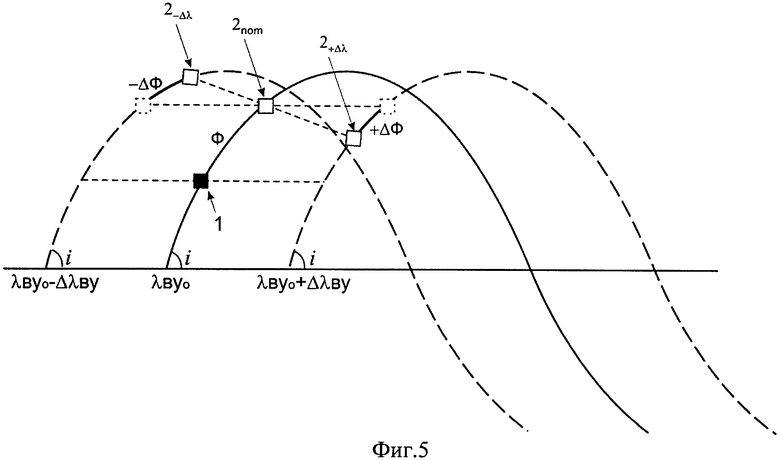
фиг.5 представляет возможную геометрию относительного положения АКО и ПКО при заданном значении начального фазового угла и различном положении плоскости орбиты ПКО,
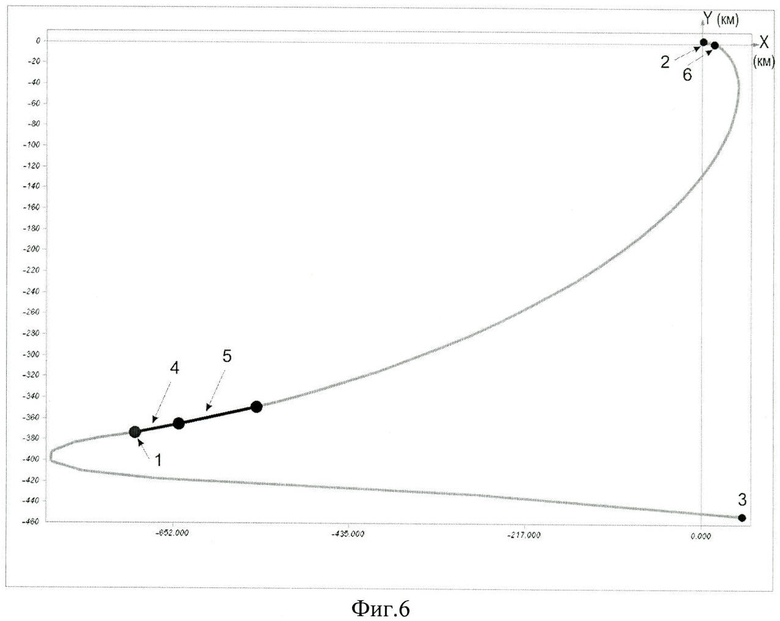
фиг.6 демонстрирует относительное движение АКО в орбитальной системе координат ПКО при реализации быстрого сближения,
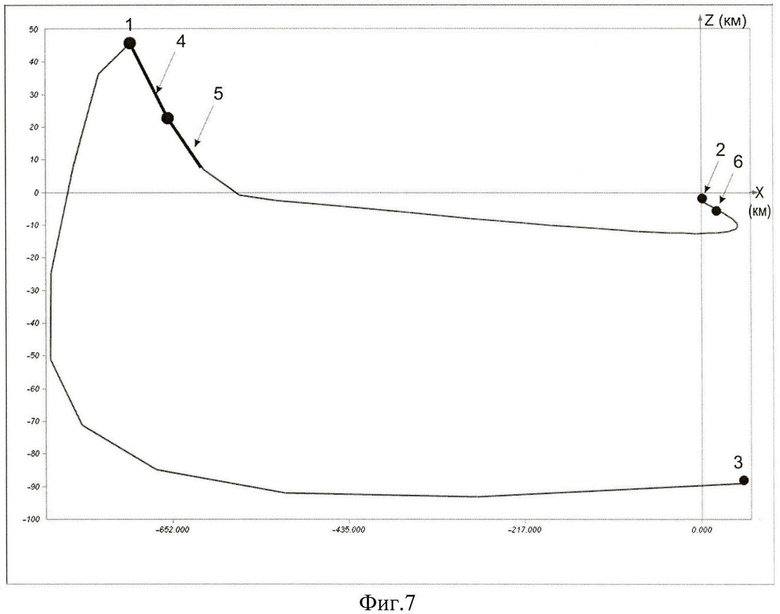
фиг.7 представляет боковое относительное движение АКО в орбитальной системе координат ПКО при реализации быстрого сближения.
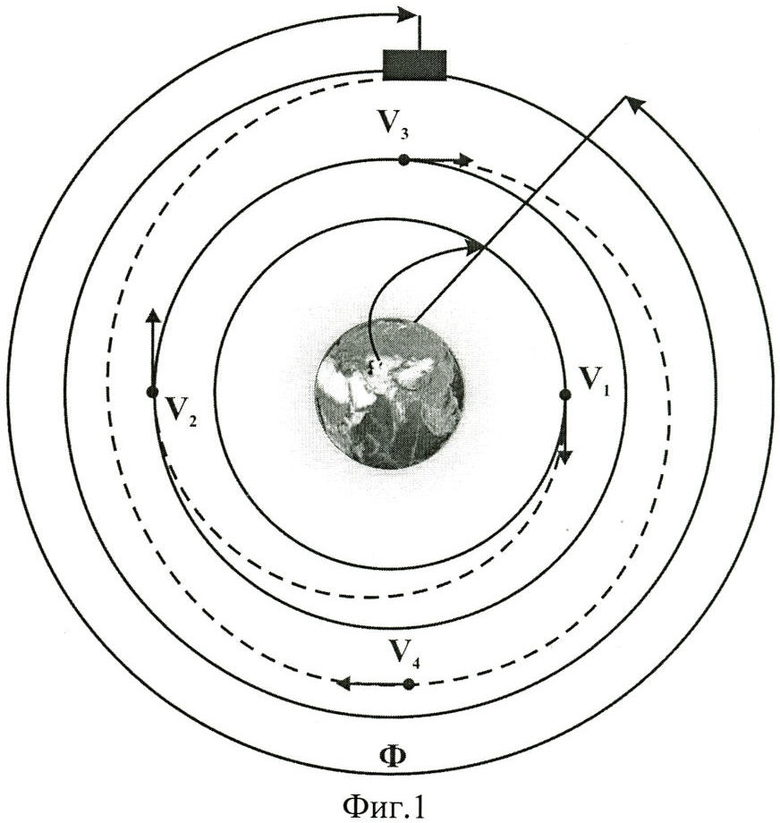
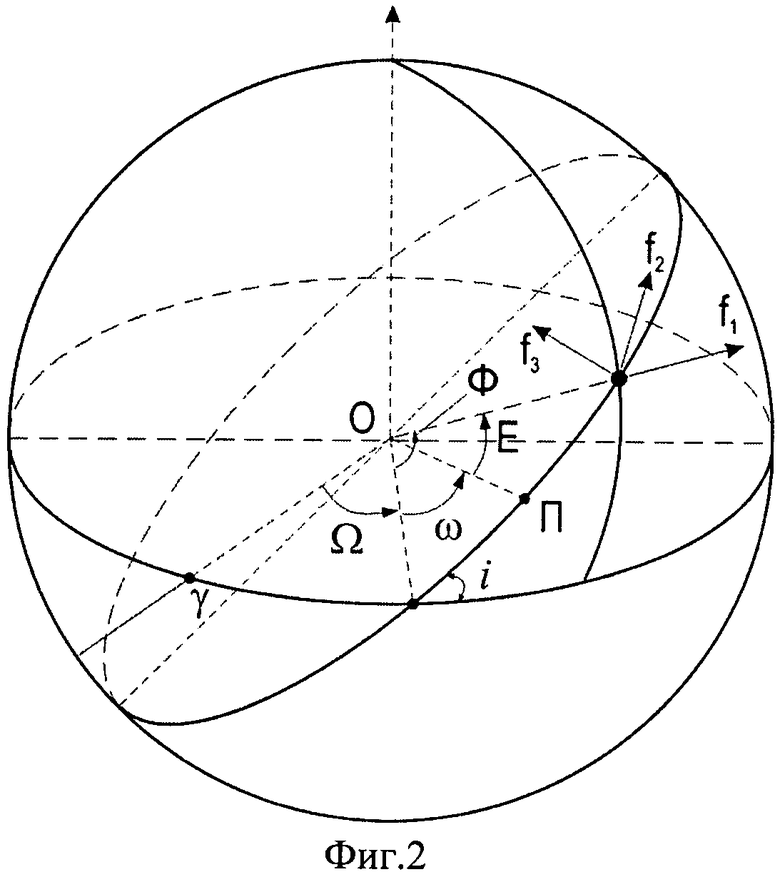
В табл.1 представлены результаты расчетов по использованию предлагаемого способа для стартовой позиции РН с координатами:
45.92° с.ш. и 63.52° в.д. (выведение в восходящую часть витка),
в табл.2 представлены результаты расчетов по использованию предлагаемого способа для стартовой позиции РН с координатами:
51.88° с.ш. и 128.36° в.д. (выведение в нисходящую часть витка).
На фиг.1 показана известная схема выведения АКО, например ПКК «Союз-ТМА» на целевую орбиту, совпадающую с плоскостью орбиты ПКО на примере МКС с последующим переходом на фазирующую орбиту, за счет проведения двухимпульсного маневра (V1 и V2) и завершающуюся переходом в окрестность МКС также за счет проведения двухимпульсного маневра (V3 и V4). На фиг.2 в геоцентрической системе координат представлены орбитальные элементы, описывающие орбитальное движение АКО и используемые в описании изобретения. Показано направление ускорения f3, перпендикулярное к плоскости орбиты АКО, обеспечивающее технический результат. Фиг.3 демонстрирует взаимное положение двух орбит с одинаковым наклонением. При этом iR - угол пересечения двух плоскостей, Ψ и соответственно 180°-Ψ - аргументы широты точки пересечения этих плоскостей, а ΔλВУ - рассогласование по долготе восходящего узла орбиты. Фиг.4 демонстрирует определение начального фазового угла в зависимости от значения долготы восходящего узла орбиты ПКО в начале стартового суточного витка АКО, при выведении последнего (поз.1) в плоскость орбиты ПКО. Так, значению λВУ0=12.7° (поз.2c1) соответствует начальный фазовый угол ΔФ0=0° (поз.2в1), а λВУ0=18.6° (поз.2с2) соответствует начальный фазовый угол ΔФ0=90° (поз.2в2). На фиг.5 представлены три положения ПКО, отличающиеся по значению восходящего узла орбиты, в момент выведения АКО. Долготе λВУ0 соответствует совпадение плоскостей орбит АКО (поз.1) и ПКО с номинальным начальным фазовым углом Ф (поз.2nom). Долготе λВУ0+ΔλВУ соответствует время старта АКО, обеспечивающее начальный фазовый угол Ф+ΔФ (поз.2+Δλ), где ΔФ=180°-2Ψ - поправка к номинальному фазовому углу, а долготе λВУ0-ΔλВУ соответствует время старта АКО, обеспечивающее начальный фазовый угол Ф-ΔФ (поз.2-Δλ), где Ψ аргумент широты точки пересечения двух плоскостей с одинаковым наклонением (фиг.3). В качестве примера для варианта начального рассогласования плоскостей ΔλВУ0-5° представлено относительное движение АКО в системе координат ПКО (поз.2) в плоскости орбиты ПКО (фиг.6) и из плоскости орбиты ПКО (фиг.7). Относительное движение показано от момента старта РН с АКО (поз.3). Сразу после выведения (поз.1) проводятся два маневра ΔV1 (поз.4) и ΔV2 (поз.5) для согласования плоскостей орбит АКО и ПКО по предложенному способу, а затем после прихода АКО в апогей орбиты проводится маневр ΔV3 (поз.6), переводящий АКО в окрестность ПКО. В табл.1 и табл.2 для двух различных стартовых позиций приведены величины потребного импульса ΔV и начального рассогласования по наклонению орбит Δi в зависимости от величины рассогласования по долготе восходящего узла орбиты ΔλВУ между орбитой ПКО и номинальной, без изменения наклонения, орбитой выведения АКО.
Как правило, для выведения на орбиту используют стартовый суточный виток, в течение которого плоскость орбиты ПКО проходит через точку старта РН. Из-за ограничения по районам падения отделяющихся частей РН запуск АКО в плоскость орбиты ПКО возможен только 1 раз в сутки. Следующая возможность по запуску возникает после поворота Земли вокруг своей оси на ~354°. Угловой диапазон суточного витка по долготе восходящего узла составляет 22.5-24° в зависимости от высоты орбиты ПКО. Этому угловому диапазону соответствует фазовый разброс начальных углов между АКО и ПКО от 0 до 360°. Допустим фазовому углу ΔФ=0° в момент выведения АКО соответствует значение долготы восходящего узла орбиты ПКО в момент прохождения экватора стартового суточного витка λВУ0. Если, к примеру, долгота восходящего узла орбиты ПКО в момент прохождения экватора будет отличаться на ~6° относительно λВУ0 в момент выведения АКО в плоскость орбиты ПКО (см. фиг.4), то начальный фазовый угол между объектами ЛФ будет ~90° (ПКО впереди АКО).
При выведении АКО на орбиту в стартовый суточный виток любого дня с заданной разницей с ПКО по аргументу широты ΔФ практически невозможно обеспечить необходимое значение λВУ0 долготы восходящего узла орбиты ПКО для совпадения плоскостей стыкуемых объектов. При одинаковом наклонении плоскости орбит объектов будут отличаться по долготе восходящего узла орбиты на ΔλВУ (фиг.5). Это обстоятельство будет препятствовать проведению «мягкой» стыковки из-за больших боковых скоростей в точке встречи. Поэтому сразу после выведения АКО необходимо провести маневр для ликвидации рассогласования по ΔλВУ. В случае если, например, энергетики РН достаточно для парирования рассогласования по λВУ в 5°, можно будет говорить о допустимом 170-градусном фазовом диапазоне для запуска ПКО. В настоящее время для реализации двухсуточной схемы сближения ПКК «Союз-ТМА» к МКС стараются обеспечить фазовый диапазон в 140° и при этом частота запусков составляет не менее 1 раза в двое суток. 170-градусный диапазон практически близок к тому, чтобы обеспечить возможность запуска 1 раз в сутки. Увеличение диапазона по λВУ0 до ±6÷7° однозначно может обеспечить одну попытку запуска в сутки без проведения дополнительных коррекций орбиты ПКО.
Из сферической геометрии можно получить следующие соотношения [5]:
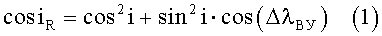
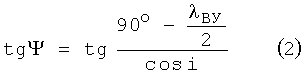
где iR - угол рассогласования плоскостей орбит АКО и ПКО,
i - угол наклонения обеих орбит,
Ψ - аргумент широты точки пересечения плоскостей орбит, причем если орбита АКО находится слева по долготе восходящего узла от орбиты ПКО, то аргумент широты точки пересечения плоскостей составит 180°-Ψ (см. фиг.3).
Для коррекции долготы восходящего узла и наклонения используется импульс, перпендикулярный к плоскости орбиты. При этом, если импульс проводится в северной части витка, то направлению вдоль вектора кинетического момента орбиты соответствуют смещение долготы в западном направлении и увеличение наклонения. В противном случае: к смещению долготы в восточном направлении и уменьшению наклонения. Наиболее выгодное положение на орбите для проведения коррекции рассогласования долготы восходящего узла орбит - точки пересечения плоскостей АКО и ПКО, которые, как правило, располагаются недалеко от точек апексов с Ф=90° и Ф=270°, где Ф - аргумент широты орбиты. В зависимости от точки приложения импульса определяется его влияние на изменение орбитальных элементов i и Ω, определяющих положение плоскости орбиты [6].
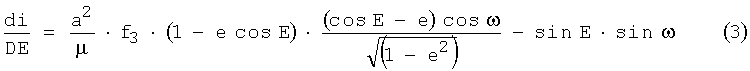
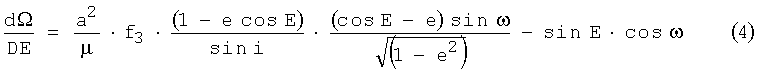
где f3 - ускорение, производимое двигательной установкой (ДУ), в направлении, перпендикулярном к плоскости орбиты (фиг.3),
µ - гравитационная постоянная небесного тела,
е - эксцентриситет орбиты,
ω - аргумент широты орбиты,
a - большая полуось орбиты.
Учитывая, что мы рассматриваем околокруговое движение с эксцентриситетом e~0, а также, что ускорение f3 определяется тягой РН Р и текущей массой М, которую можно принять постоянной, т.е.:
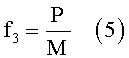
и, соответственно: 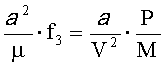
где V - средняя скорость кругового движения, формулы (3) и (4) можно упростить:
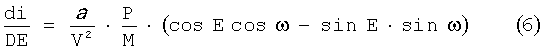
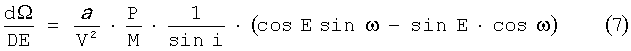
Аргумент перигея ω отсчитывается от восходящего узла орбиты до перигея. Эксцентрическая аномалия отсчитывается от положения перигея орбиты (фиг.2). Поэтому аргумент широты орбиты будет связан с углами Е и ω следующей формулой:
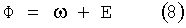
Так как ускорение f3 имеет ограниченное значение, то исполнение любого импульса будет производиться в течение некоторого времени Δt. За это время аргумент широты орбиты изменится от Ф до Ф+Δφ. С целью упрощения можно принять, что импульс прикладывается в середине углового интервала Δφ, т.е. в точке с аргументом широты 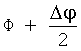 и производные по изменению орбитальных параметров i и Ω должны быть вычислены в точке
и производные по изменению орбитальных параметров i и Ω должны быть вычислены в точке 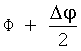 .
.
Так как λВУ аналогично Ω, то согласно (7) можно записать:
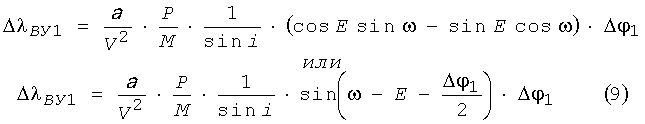
За время исполнения импульса ΔV1 наклонение орбиты i получит возмущение Δi1, вычисляемое из формулы (6), как:
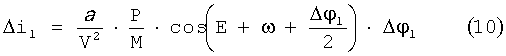
Полученное рассогласование по наклонению необходимо парировать вторым маневром с вектором тяги, направленным в противоположную сторону. Если проводить второй маневр с той же тягой, то эффективность этой операции будет невысока, т.к. включение ДУ будет близко к точке проведения первого маневра и при коррекции наклонения Δi мы получим практически такое же изменение плоскости орбиты по ΔλВУ, но с обратным знаком. Выходом из этой ситуации является максимально возможное дросселирование тяги ДУ и соответственно смещение интервала исполнения второго маневра в область более эффективных точек приложения импульса для изменения наклонения орбиты. Если принять, что тяга f3 уменьшается в k раз, то угловой интервал исполнения второго маневра Δφ2 соответственно увеличится приблизительно в k раз с поправкой на коэффициент эффективности, связанный со сдвигом точки приложения импульса вдоль орбиты. С целью упрощения принимаем, что импульс прикладывается в середине интервала, т.е. в точке с 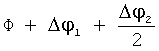 и производные по изменению орбитальных параметров i и λВУ вычисляются в этой точке. Используя формулы (6) и (7), получим:
и производные по изменению орбитальных параметров i и λВУ вычисляются в этой точке. Используя формулы (6) и (7), получим:
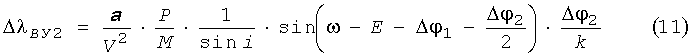
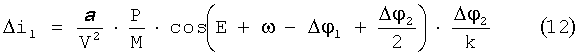
Так как ΔλВУ=ΔλВУ1-ΔλВУ2 и Δi1+Δi2=0, то используя уравнения (9)÷(12), можно получить значения угловых интервалов - Δφ1 и Δφ3 из решения следующей системы трансцендентальных уравнений (13) и (14):
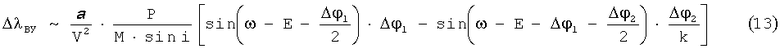
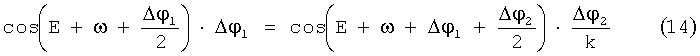
Зная угловую длительность проведения маневров Δφ1 и Δφ2, можно получить значения для импульсов скорости ΔV1 и ΔV2
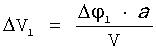 и
и 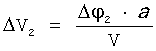
Предлагаемый способ управления может быть использован при проведении сближения и стыковки ПКК с орбитальной станцией МКС. Особенно полезно использование этого метода при проведении спасательной миссии, когда фактор времени доставки экипажа на борт МКС становится решающим.
Для расчета времени старта АКО с заданным начальным угловым рассогласованием ΔФ необходимо иметь вектор состояния ПКО на момент выведения АКО. Знание этого вектора обеспечивается наземными средствами измерения орбиты типа «Кама» и «Квант» или бортовой аппаратурой АСН-М, использующей измерения систем спутниковой навигации GPS и ГЛОНАСС.
Данные по времени проведения и значению маневров для совмещения плоскостей орбит АКО и ПКО рассчитываются по вектору состояния ПКО и заносятся в полетное задание РН или АКО непосредственно перед запуском РН с АКО.
После выведения АКО на целевую орбиту необходимо провести развороты ДУ последней ступени РН или АКО для выдачи импульса в направлении, перпендикулярном плоскости орбиты. Для управления ориентацией РН могут быть использованы либо качение маршевых двигателей, либо их раздельное включение (в случае, если на последней ступени несколько двигателей) для создания управляемого момента по каналу рыскания. У некоторых РН для этой цели могут быть также использованы специальные верньерные двигатели [7]. Для минимизации влияния разворота на параметры целевой орбиты целесообразно его проведение с дросселированием тяги. В случае, если разворот проводится средствами АКО, используются двигатели ориентации АКО.
Выполнение дополнительных маневров для совмещения плоскостей орбит стыкуемых объектов может быть обеспечено средствами РН в случае, если допустимая выводимая масса РН превосходит массу АКО, т.е. имеется избыток выводимой массы, заключенный в топливо РН или собственно средствами АКО при наличии у него необходимого количества топлива. В случае выполнения маневра с использованием топлива АКО или, если РН имеет возможность повторно запускаться, можно свести способ управления до выполнения только одного маневра, за счет смещения углового интервала Δφ для выполнения первого маневра в окрестность точки пересечения плоскостей орбит АКО и ПКО (см. фиг.4). В этом случае весь сформированный импульс пойдет на ликвидацию рассогласования плоскостей по восходящему узлу орбиты без возникновения рассогласования по наклонению орбиты Δi. В варианте достаточности топлива у АКО первый маневр выполняет РН сразу после выведения, а второй маневр ДУ АКО в окрестности прохождения экватора с целью оптимизации расхода топлива.
Для проведения сравнительного анализа были выполнены расчеты по использованию предложенного способа для двух стартовых позиций РН с координатами:
№1: 45.92° с.ш. и 63.52° в.д. (выведение в восходящую часть витка)
№2: 51.88° с.ш. и 128.36° в.д. (выведение в нисходящую часть витка)
АКО выводился на целевую орбиту с параметрами Hmin/Hmax=135/440 км и наклонением i=51.6°. Моделировался начальный разброс по долготе восходящего узла для следующих вариантов ΔλВУ=±5°. Среднее ускорение f3 составляло ~1.5g. Коэффициент дросселирования ДУ k для проведения второго маневра принимал следующие значения: k=0.1, 0.05, 0.025. Также рассмотрен случай повторного включения ДУ в окрестности точки пересечения плоскостей АКО и ПКО. Результаты вычислений сведены в табл.1 и 2, соответственно для стартовых позиций РН №1 и №2. Расчеты проведены с помощью программного обеспечения Satellite Tool Kit 8.0 и подтверждают получение необходимого результата. Наилучшая эффективность достигается при максимальном дросселировании ДУ РН. Наиболее оптимальный вариант с точки зрения расхода топлива появляется в случае возможности повторного включения ДУ РН в окрестности точки пересечения плоскостей АКО и ПКО. Сравнение двух стартовых позиций показывает, что для позиции №1 использование описанного способа управления примерно в 1.5 раз эффективнее за счет выведения АКО в более оптимальное положение на орбите (в район апекса).
Список литературы
1. Wigbert Fehse (2003) "Automated Rendezvous and Docking of Spacecraft", Cambrige University press.
2. NASA Press kit (1966) "Project Gemini-11" - прототип, http://www.scribd.com/doc/11483557/Gemini-11-Press-Kit.
3. Утвержден график полетов к МКС в 2010 году. Ж. Новости космонавтики, т.20, №1 (324), 2010 г., стр.25.
4. R.Murtazin, S.Budylov "Short Rendezvous Missions for Advanced Russian Human Spacecraft", 60th International Astronautical Congress, 12th-16th October 2009, Daejeon, Republic of Korea.
5. James R.Wertz (2001) "Mission Geometry; Orbit and Constelation Design and Management", Space Technology Library.
6. J.E.Pollard (2000) "Simplified Analysis of Low-Thrust Orbital Maneuvers", Aerospace report № TR-2000(8565)-10.
7. Steven J.Isakowitz (2004) "International Reference Guide to Space Launch Systems" Forth edition.
Способ управления движением активного космического объекта, стыкуемого с пассивным космическим объектом
Изобретение относится к операциям стыковки, в частности, пилотируемого космического корабля с международной космической станцией. Способ включает выведение активного космического объекта (АКО) ракетой-носителем на целевую орбиту с отклонением по долготе ее восходящего узла, но с заданным рассогласованием по аргументу широты. Затем в перпендикулярном направлении к плоскости выведения выполняют первый маневр АКО для изменения долготы восходящего узла орбиты. Далее в противоположном направлении выполняют второй маневр для ликвидации рассогласования по наклонению целевой орбиты, возникшему после первого маневра. Этот маневр выполняют с дросселированием тяги двигателя АКО, создавая дополнительное отклонение по долготе восходящего узла и совмещая плоскости орбит стыкуемых объектов. За счет формирования необходимого начального углового рассогласования между объектами сокращается продолжительность сближения АКО с пассивным космическим объектом (ПКО) вплоть до одного витка. Техническим результатом изобретения является сокращение времени операции стыковки АКО и ПКО при сохранении приемлемой частоты возможных дат старта АКО и без проведения дополнительных коррекций орбиты ПКО. 7 ил., 2 табл.
Способ управления движением активного космического объекта, стыкуемого с пассивным космическим объектом, включающий выведение активного космического объекта на целевую орбиту, отличающийся тем, что производят выведение активного космического объекта на целевую орбиту с отклонением по долготе восходящего узла орбиты от орбиты пассивного космического объекта на величину ΔλВУ, но с заданным рассогласованием по аргументу широты ΔФ, после чего в перпендикулярном направлении к плоскости выведения выполняют первый маневр в угловом интервале Δφ1 от точки выведения на целевую орбиту для изменения долготы восходящего узла орбиты на ΔλВУ1 путем формирования импульса ΔV1, а затем в противоположном направлении в угловом интервале Δφ2 выполняют второй маневр с дросселированием тяги двигателя активного космического объекта для ликвидации рассогласования по наклонению целевой орбиты Δi1, возникшего после первого маневра, и создания дополнительного отклонения по долготе восходящего узла ΔλВУ2 путем формирования импульса ΔV2, приводящего к совпадению плоскостей орбит стыкуемых объектов.
| Двухтактный двигатель внутреннего горения | 1924 |
|
SU1966A1 |
| СПОСОБ УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ РАЗГОННОГО БЛОКА НА УЧАСТКЕ ДОРАЗГОНА | 2007 |
|
RU2350521C1 |
| СПОСОБ УПРАВЛЕНИЯ КИНЕТИЧЕСКИМ МОМЕНТОМ КОСМИЧЕСКОГО АППАРАТА В ПРОЦЕССЕ КОРРЕКЦИИ ОРБИТЫ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2001 |
|
RU2178761C1 |
| СПОСОБ И СИСТЕМА ВЫВЕДЕНИЯ НА ЗАДАННУЮ ОРБИТУ КОСМИЧЕСКОГО АППАРАТА С ИСПОЛЬЗОВАНИЕМ ДВИГАТЕЛЕЙ, ОБЛАДАЮЩИХ БОЛЬШИМ УДЕЛЬНЫМ ИМПУЛЬСОМ | 1997 |
|
RU2212363C2 |
| US 3700193 A, 24.10.1972. | |||
Авторы
Даты
2012-01-20—Публикация
2010-05-24—Подача