Изобретение относится к способам формирования математической модели человека-оператора (например, летчика) при отслеживании им заданных положений (отклонений) штурвала управления по сигналу ошибки отклонения на директорном приборе. Под математической моделью человека-оператора понимается математическая связь ошибки отклонения штурвала в виде отклонения стрелки директорного прибора и задаваемое ею положение штурвала (или усилие, прикладываемое к штурвалу).
Способ необходим при замене человека-оператора его математической моделью, например, для имитации действий человека-оператора (например, летчика) при математическом моделировании и анализе процессов директорного управления динамическим объектом, например самолетом.
Известен способ формирования математической модели собственной инерционности человека-оператора (прототип) (см. Доброленский Ю.П., Иванова В.И., Поспелов Г.С. Автоматика управляемых снарядов. - М: Государственное научно-техн. изд-во ОБОРОНГИЗ, 1963. - 548 с.) в виде передаточной функции последовательного соединения звена чистого запаздывания, апериодического и форсирующего звеньев.
Недостатком этой модели является ее неполнота и неточность, например, при отслеживании человеком-оператором по директорному прибору заданных положений штурвала, соответствующих различным временным функциям. Например, если заданное положение штурвала представляет собой ступенчатую функцию, то оказывается необходимым добавление к передаточной функции прототипа интегрирующего звена (Оболенский Ю.Г., Похваленский В.Л., Теряев Е.Д., Якубович М.М. Разработка и исследование модели действий летчика при позиционировании ручки управления самолетов. - М.: Наука// Проблемы машиностроения и надежности машин, 2004, №5. – С. 70-77). Однако эксперименты показывают, что при экспоненциальной функции заданных положений штурвала целесообразно добавление не интегрирующего, а апериодического звена с постоянной времени, равной постоянной времени изображения Лапласа задаваемой экспоненты.
Предлагаемое решение отличается тем, что формируют и дополнительно подключают математическую модель оценок переменных состояния предполагаемой динамической модели задатчика-генератора заданных положений штурвала, соответствующую, например, изображению Лапласа реальной временной функции заданных положений, так, что сигнал выхода математической модели собственной инерционности человека-оператора через коэффициенты усиления суммируют с входными сигналами каждого интегратора математической модели оценок переменных состояния задатчика-генератора, т.е. с производными ее переменных состояния, как в известных наблюдающих устройствах, а взвешенная сумма этих оценок, соответствующая динамической модели задатчика-генератора, является выходом полной математической модели человека-оператора и входом штурвала.
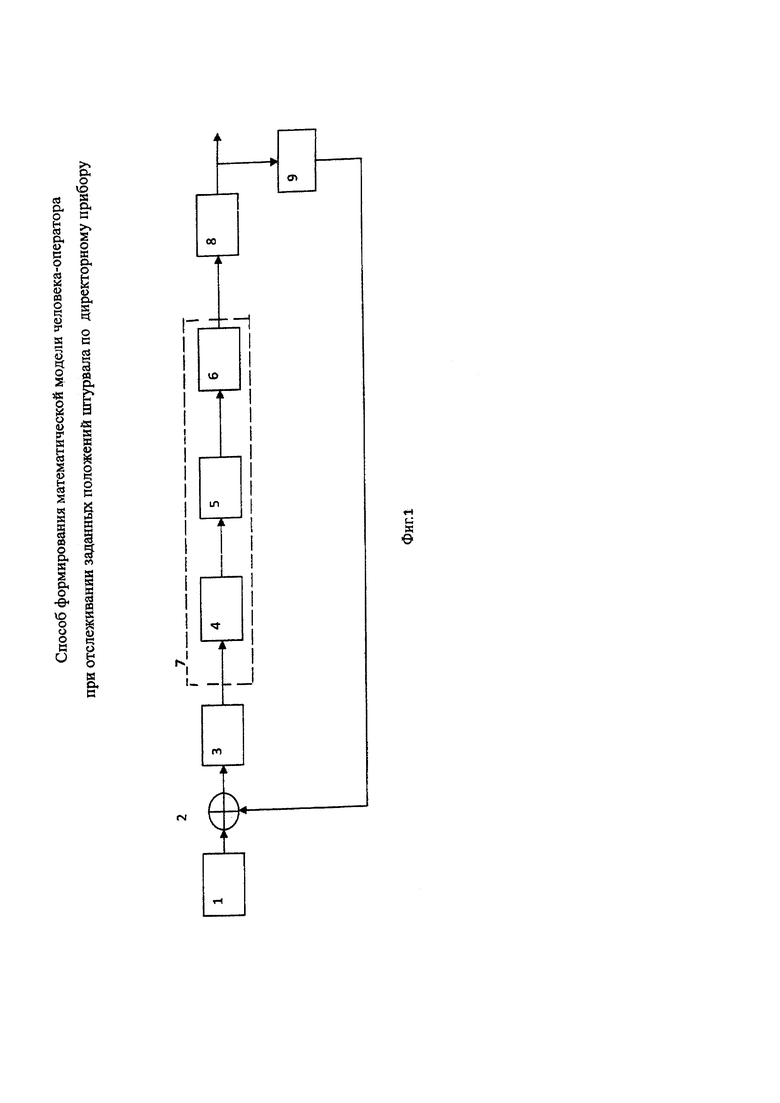
Суть предложенного решения поясняется Фиг. 1, где приведена блок-схема имитации процесса отслеживания человеком-оператором по директорному прибору заданных положений штурвала с предложенным дополнением к модели собственной инерционности человека-оператора.
На Фиг. 2 представлены переходные процессы отслеживания ступенчатых заданных положений штурвала в стендовом эксперименте с реальным участием человека-оператора.
На Фиг. 3 представлены переходные процессы имитационного математического моделирования того же процесса, что и на Фиг. 2, с соответствующей входному сигналу математической моделью человека-оператора и моделью штурвала с выбранным коэффициентом усиления между двумя частями передаточной функции человека-оператора.
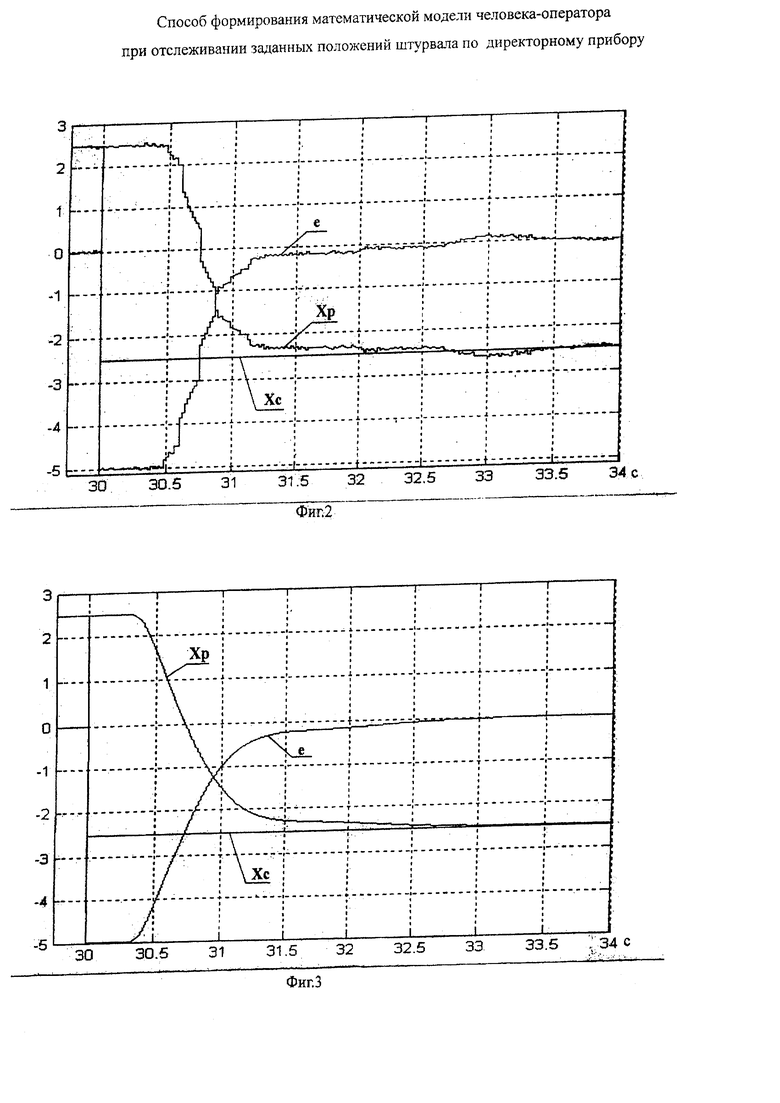
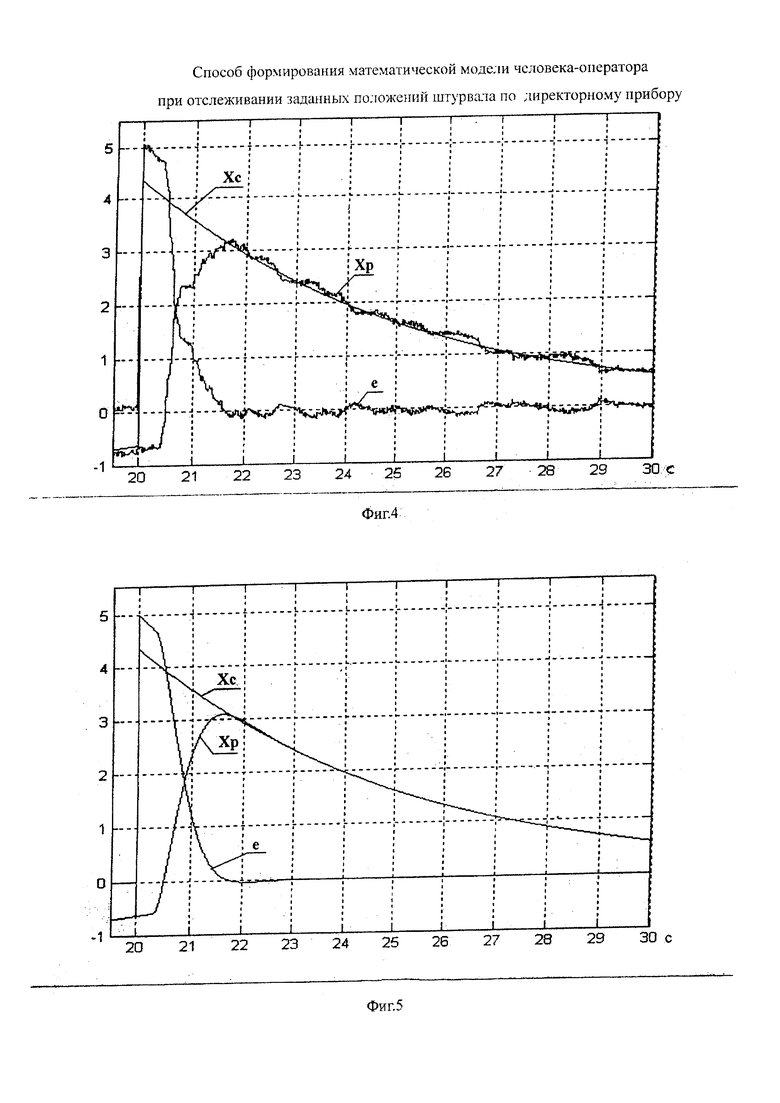
На Фиг. 4 представлены переходные процессы отслеживания экспоненциальных заданных положений штурвала в стендовом эксперименте с реальным участием человека-оператора.
На Фиг. 5 представлены переходные процессы имитационного математического моделирования того же процесса, что на Фиг. 4, с соответствующей входному сигналу математической моделью человека-оператора и моделью штурвала с выбранным коэффициентом усиления между двумя частями передаточной функции человека-оператора.
Принятые обозначения:
1 - задатчик-генератор заданных положений штурвала;
2 - сумматор;
3 - директорный прибор (ДП);
4 - математическая модель собственной инерционности человека-оператора (прототип);
5 - вектор-столбец коэффициентов усиления (в общем случае переменных);
6 - математическая модель оценок переменных состояния динамической модели задатчика-генератора, соответствующая, например, преобразованию Лапласа временной функции заданных положений штурвала;
7 - полная математическая модель человека-оператора;
8 - математическая модель штурвала;
9 - модель датчика сигнала отклонения штурвала Хш;
хз - временная функция заданных положений (отклонений) штурвала (выход блока 1);
хш=хр - отклонение модели штурвала (выход блока 8);
е - ошибка отклонения штурвала (е=хз-хш) (выход сумматора 2);
еп - выход математической модели собственной инерционности человека-оператора (блока 4);
х - вектор переменных состояния предполагаемой или реальной динамической модели задатчика-генератора заданных положений штурвала;
х(0) - вектор начальных значений переменных состояния динамической модели задатчика-генератора;
хм - вектор оценок переменных состояния математической модели задатчика-генератора в математической модели человека-оператора;
хзм - оценка задаваемого моделью человека-оператора положения штурвала (выход блока 6);
А - матрица обратных связей динамической модели задатчика-генератора;
Н - матрица-строка формирования заданной временной функции х3 из компонент вектора х;
К - векторный коэффициент усиления в математической модели человека-оператора в общем случае переменный по времени (блок 5);
Wп(s)=e-τs (T1s+1)/(T2s+1) - передаточная функция собственной инерционности человека-оператора (модель прототипа) (блок 4);
Wш(s) - передаточная функция модели штурвала (блок 8).
Последовательность действий по способу.
Формируют математическую модель оценок переменных состояния динамической модели задатчика-генератора заданных положений штурвала на основе предполагаемой динамической модели задатчика-генератора, например, в виде линейных векторных дифференциального и алгебраического уравнений


где х - n-мерный вектор переменных состояния генератора заданных положений штурвала с начальным условием х(0), А - матрица (nxn), Н - матрица-строка (nx1). Эти уравнения и их параметры, если они стационарны, должны соответствовать преобразованию Лапласа временной функции заданных положений штурвала. Для некоторых задач система типа (1), (2) может быть нестационарной и нелинейной.
Соответственно предложенному решению математическая модель вектора оценок переменных состояния задатчика-генератора и задаваемого моделью человека-оператора положения штурвала, запишется в виде уравнений
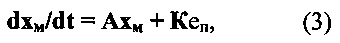

Здесь выход модели собственной инерционности человека-оператора (прототипа) еп корректирует, как это требуется в наблюдающем устройстве, переменные состояния модели (Кузовков Н.Т. Модальное управление и наблюдающие устройства. - М.: Машиностроение, 1976. - 184 с).
Уравнения (3), (4) представляют предлагаемое дополнение к математической модели прототипа.
Рассмотрим на примерах получение полной математической модели человека-оператора.
Пример 1. Пусть заданные положения штурвала представляют собой функцию в виде знакопеременных постоянных значений, равных по модулю величине 2,5. Тогда, например, на участке положительного значения хз=2,5 преобразование Лапласа будет равно 2,5/s, а уравнения динамической модели задатчика-генератора будут иметь вид
dx/dt=0,
хз=х,
х(0)=2,5.
Соответственно предлагаемое дополнение к математической модели собственной инерционности человека-оператора будет определяться уравнениями
dxм/dt=keп,
хзм=хм.
В результате полная математическая модель человека-оператора соответствует передаточной функции
Wп(s)=e-τs k(T1s+1)/((T2s+1)s),
где предлагаемое дополнение к модели прототипа представляет собой интегрирующее звено k/s.
Конкретные значения всех констант τ, k, Т1, Т2 могут быть определены по результатам стендового эксперимента для конкретного человека, участвовавшего в эксперименте.
На фиг. 2 приведен фрагмент (с 30-й по 34-ю секунду) процессов отслеживания конкретным человеком-оператором заданных ступенчатых положений штурвала в физическом (стендовом) эксперименте, где показаны заданные положения хз=хс и получающиеся при отслеживании отклонения штурвала хш=хр, а также величина ошибки отклонения e(t). При этом хз=хш=2,5 при t<30 с и хз=-2,5 при t>30 с, а начальная ошибка е=0 при t<30 с и е=5 при t>30 с. В результате ошибка обнуляется через 1,5 с.
На фиг. 3 приведен аналогичный фрагмент математического имитационного моделирования на ПЭВМ для тех же заданных положений штурвала с выбранными подходящими значениями всех параметров математической модели конкретного человека-оператора τ=0,3, k=1,23, Τ1=0,27, Т2=0,15. Передаточная функция штурвала имела вид
Wш(s)=200/(s2+23s+200).
Как видно, имитационное математическое моделирование с полученной полной математической моделью человека-оператора хорошо повторяет стендовое.
Пример 2. Пусть заданное положение штурвала представляет знакопеременные отрезки экспоненциальных функций времени хз=cie-0,2t, где величина ci меняется от 2,5 до 4,5 и может иметь разные знаки. Тогда, например, на участке положительного значения ci=2,5 преобразование Лапласа будет равно 2,5/(s+0,2), а уравнения динамической модели задатчика-генератора будут иметь вид
dx/dt=-0,2х,
xз=x,
х(0)=2,5.
Соответственно предлагаемое дополнение к математической модели собственной инерционности человека-оператора будет определяться уравнениями
dxм/dt=-0,2хм+kеп,
xзм=xм.
В результате полная математическая модель человека-оператора соответствует передаточной функции
Wп(s)=e-τs k(T1s+1)/((T2s+1)(s+0,2)),
где предлагаемое дополнение к модели прототипа представляет собой апериодическое звено с передаточной функцией k/(s+0,2).
Конкретные значения всех констант τ, k, Τ1, Т2 могут быть определены по результатам стендового эксперимента для конкретного человека, участвовавшего в эксперименте.
На фиг. 4 приведен фрагмент (с 20-й по 30-ю секунду) процессов отслеживания заданных экспоненциальных функций положений штурвала в стендовом эксперименте, где показаны заданные положения хз=4,4е-0,2t и получающиеся при отслеживании отклонения штурвала xp(t), а также величины ошибки отклонения e(t)=xз(t)-xp(t). При этом хз=хр=-0,6 при t<20 с и хз=4,4 при t>20 с, а начальная ошибка е=0 при t<20 с и е=5 при t>20 с. В результате ошибка обнуляется через 1,5 с.
На фиг. 5 приведен аналогичный фрагмент математического имитационного моделирования на ПЭВМ тех же процессов, что и на Фиг. 4, с выбранными значениями параметров τ=0,3, k=1,08, Τ1=0,18, Т2=0,15.
Как видно, имитационное моделирование с полученной полной математической моделью конкретного человека-оператора, как и в примере 1, хорошо повторяет стендовое.
Рассмотрение этих и других примеров заданных положений штурвала позволяет сделать общий вывод о том, что добавляемая часть математической модели человека-оператора соответствует динамической модели задатчика-генератора.
Технический результат от использования предложенного способа формирования математической модели человека-оператора заключается в повышении точности математического имитационного моделирования на ПЭВМ и анализа процессов директорного управления, если оно основано на системе отслеживания человеком-оператором заданных положений штурвала, как это рекомендуется в работе (Елисеев В.Д., Клюев Е.Д., Петрин К.В., Теряев Е.Д. Повышение качества директорного управления динамическим объектом. - М., Проблемы управления, 2012, №4. – С. 69-74).
Новизна предложенного изобретения подтверждается отличительной частью формулы изобретения, что не было известно до сих пор, а именно к известной математической модели собственной инерционности человека-оператора для повышения точности добавляют наблюдающее устройство в виде корректируемой человеком-оператором математической модели оценивания переменных состояния динамической модели задатчика-генератора заданных положений штурвала.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ ДИРЕКТОРНОГО УПРАВЛЕНИЯ ПО ЭТАЛОННЫМ СИГНАЛАМ МОДЕЛИ ОБЪЕКТА | 2010 |
|
RU2454693C1 |
| ПУЛЬТ, СИСТЕМА И СПОСОБ РУЧНОГО УПРАВЛЕНИЯ И СТАБИЛИЗАЦИИ РЕГУЛИРУЕМОЙ ВЕЛИЧИНЫ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА (ВАРИАНТЫ) "АРЖЕСАН" | 1996 |
|
RU2128600C1 |
| Способ адаптивного управления мостовым краном | 2024 |
|
RU2830910C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ МОЩНОСТЬЮ ЯДЕРНОЙ ЭНЕРГЕТИЧЕСКОЙ УСТАНОВКИ С РЕАКТОРОМ ВОДО-ВОДЯНОГО ТИПА | 2003 |
|
RU2278427C2 |
| Адаптивная система управления для объектов с изменяющимся запаздыванием | 1984 |
|
SU1191884A1 |
| Самонастраивающаяся система | 1984 |
|
SU1241192A1 |
| СПОСОБ КОМАНДНОГО ТЕЛЕУПРАВЛЕНИЯ РАКЕТОЙ | 2004 |
|
RU2280227C1 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ДВУХЭТАПНЫМ ИДЕНТИФИКАТОРОМ И НЕЯВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ | 2002 |
|
RU2231819C2 |
| Пространственная имитационная модель системы управления автоматическим маневренным летательным аппаратом | 2019 |
|
RU2735418C2 |
| ИМИТАЦИОННАЯ МОДЕЛЬ СИСТЕМЫ УПРАВЛЕНИЯ ВОЗДУШНОЙ МИШЕНЬЮ НА ОСНОВЕ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА ИЗ СОСТАВА МИШЕННОГО КОМПЛЕКСА | 2020 |
|
RU2782035C2 |
Изобретение относится к способу формирования математической модели человека-оператора в системе отслеживания заданных положений штурвала по сигналу ошибки на директорном приборе. Формируют математическую модель в виде последовательного соединения звеньев чистого запаздывания, апериодического и форсирующего, математической модели оценок переменных состояния динамической модели задатчика-генератора заданных положений штурвала, выход которой через коэффициенты усиления суммируют с входными сигналами каждого интегратора математической модели оценок переменных состояния задатчика-генератора, получают на выходе математической модели человека оператора и входе штурвала сигнал, равный сумме взвешенных оценок переменных состояния задатчика-генератора определенным образом. Обеспечивается повышение точности математического имитационного моделирования и анализа процессов директорного управления. 5 ил., 2 пр. 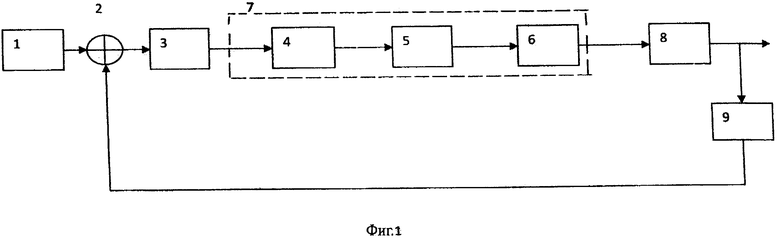
Способ формирования математической модели человека-оператора в системе отслеживания заданных положений штурвала по сигналу ошибки на директорном приборе, заключающийся в том, что формируют математическую модель собственной инерционности человека-оператора в виде последовательного соединения звена чистого запаздывания, апериодического и форсирующего звеньев, входом которой является наблюдаемое им на директорном приборе отклонение планки, метки или стрелки от нулевого положения, пропорциональное ошибке отклонения штурвала от заданного положения, отличающийся тем, что формируют и дополнительно подключают математическую модель оценок переменных состояния динамической модели задатчика-генератора заданных положений штурвала, соответствующую, например, изображению Лапласа реальной временной функции этих положений, так что выход математической модели собственной инерционности человека-оператора через коэффициенты усиления суммируют с входными сигналами каждого интегратора математической модели оценок переменных состояния задатчика-генератора, т.е. с производными ее переменных состояния, как в известных наблюдающих устройствах, а взвешенная сумма этих оценок является выходом полной математической модели человека-оператора и входом штурвала.
| СИСТЕМА ОБРАБОТКИ И АНАЛИЗА ПОЛЁТНОЙ ИНФОРМАЦИИ В РЕАЛЬНОМ ВРЕМЕНИ И УПРАВЛЕНИЯ ЛЁТНЫМ ЭКСПЕРИМЕНТОМ | 2013 |
|
RU2562409C2 |
| ЛЕТНО-МОДЕЛИРУЮЩИЙ ПИЛОТАЖНЫЙ КОМПЛЕКС | 2006 |
|
RU2310909C1 |
| СПОСОБ САМОНАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ ОБЪЕКТОМ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2005 |
|
RU2304298C2 |
| US 8091679 B2, 10.01.2012 | |||
| US 20100228441 A1, 09.09.2010. | |||
Авторы
Даты
2018-01-23—Публикация
2016-05-23—Подача