Изобретение относится к области судовождения, в частности, к автоматическому управлению движением судна-катамарана с двумя винторулевыми колонками (ВРК) с конкретным применением к маломерному роботизированному научно-исследовательскому судну для комплексного экологического мониторинга морской прибрежной акватории Черного моря, а также озер и рек, с базированием в г. Севастополе, в частности, для безэкипажного режима эксплуатации судна. Для удержания судна на предварительно спланированном маршруте необходимо управлять им в автоматическом режиме таким образом, чтобы в случае отклонения от маршрута судно возвращалось на маршрут. При этом могут быть ситуации (при обходе внезапно появившегося препятствия, при движении в узкостях и т.п.), когда маневр судна производится при большом угле поворота винторулевой колонки. При этом динамика судна оказывается нелинейной и методы управления должны быть адекватными. В судовождении такие маневры судна называют «сильными» [1].
Способы автоматического управления судами конструируют либо без использования математических моделей, либо с их использованием.
Так, в патентах [2-5] предлагаются способы, в которых управление осуществляется по информации от спутников и бортовых измерителей с использованием «инженерных» приемов формирования управляющих сигналов, т.е. интуитивно понятных алгоритмов, которые не требуют использования математической модели судна. Так, например, в [4] угол отклонения пера руля (перекладки) рассчитывается путем численного решения линейного дифференциального уравнения, правая часть которого зависит от отклонения курсового угла от заданного, угловой скорости судна, а также от угла перекладки руля, с тремя неопределенными коэффициентами.
При использовании носовых подруливающих устройств предлагается дополнительно использовать алгоритм в виде линейного дифференциального уравнения относительно поперечной управляющей силы, правая часть которого зависит от угла дрейфа, интеграла от угла дрейфа, а также от поперечной управляющей силы, с тремя неопределенными коэффициентами [5]. При этом используются алгоритмы расчета «упреждающих» точек, от которых реализуются предварительно рассчитанные программные управления для поворота судна на новый курс, а также условия обратного включения режима стабилизации вдоль заданного курса K*.
Наряду со способами, защищенными патентами, в журнальных публикациях предлагаются и другие, большинство из которых основаны на предварительной линеаризации исходной модели судна либо использовании ПИД-регуляторов. Общим недостатком указанных методов, а также и других (например, [6], [7]), основанных на использовании линейных и нелинейных обратных связей от координат состояния, является то, что они содержат неопределенные коэффициенты, которые заранее неизвестны и могут зависеть от условий функционирования. Для приспособления к условиям функционирования используются принципы адаптивного и интеллектуального управления [8, 9]. В меньшей степени такие недостатки присущи методам, основанным на использовании математических моделей объекта управления [10-12].
Для разработки алгоритмов управления «сильными» маневрами с использованием математических моделей судов рекомендуется [1] использовать упрощенные нелинейные модели Номото в виде дифференциальных уравнений второго порядка относительно угловой скорости с неопределенными коэффициентами. При этом для построения указанных моделей требуется проведение экспериментов над реальным судном или его масштабной моделью с целью определения неопределенных коэффициентов. Кроме того, далее необходимо решать задачу разработки алгоритма управления по нелинейной модели объекта.
В предлагаемом способе, в отличие от прототипа [4], используется относительно полная нелинейная модель движения судна-катамарана [13] в горизонтальной плоскости в виде нормальной системы дифференциальных уравнений седьмого порядка со сложными нелинейными функциями правых частей. Уравнения построены для продольной и поперечной скоростей судна в системе координат судна, его угловой скорости относительно центра масс в горизонтальной плоскости, перемещений в продольном и поперечном направлениях земной системы координат, курсового угла, угла поворота ВРК. При этом учтены следующие силы и моменты, воздействующие на судно: силы сопротивления движению судна в продольном и поперечном направлениях, упоры винтов ВРК, тормозящие моменты позиционных (зависящих от линейной скорости) и демпфирующих (зависящих от линейной и угловой скоростей) сил, управляющего воздействия на приводы ВРК. При этом ветроволновые воздействия на судно не учитывались, упоры винтов предполагались одинаковыми и постоянными, углы поворота обеих ВРК предполагались одинаковыми.
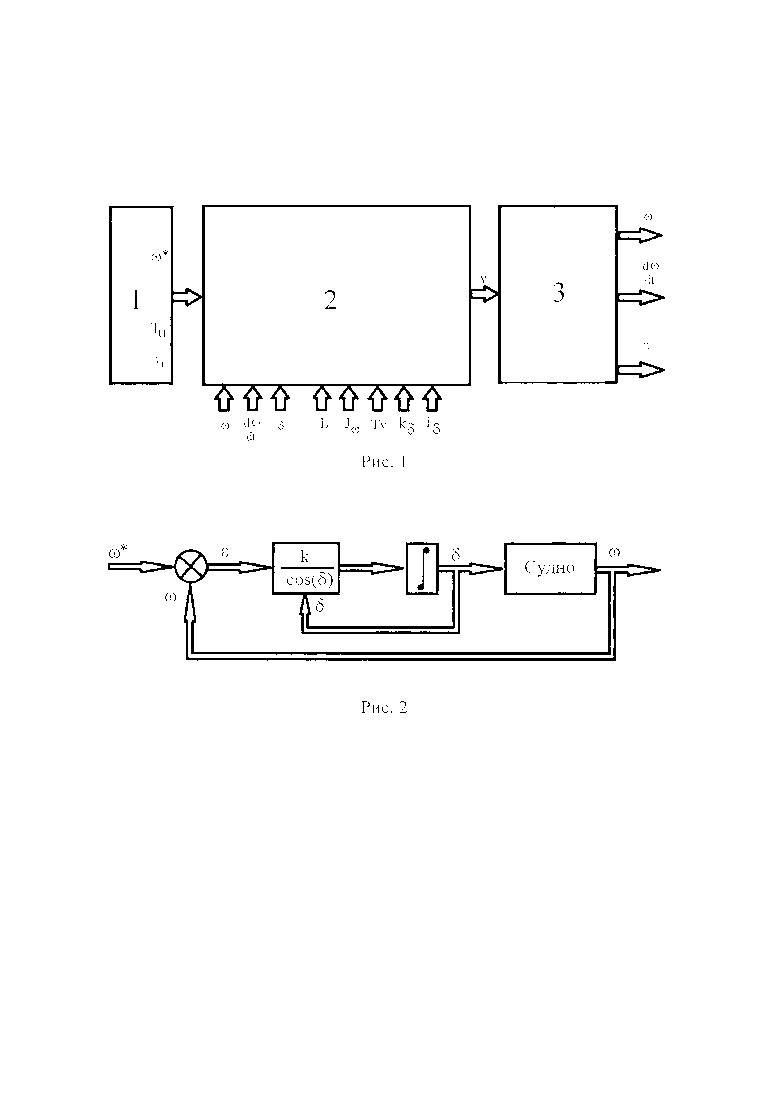
В предлагаемом способе используют сигналы (рис. 1): текущих значений угловой скорости ω и ускорения dω/dt судна в горизонтальной плоскости относительно центра масс, одинакового для двух ВРК угла поворота δ; постоянные значения: длины судна L, присоединенного момента инерции судна относительно вертикальной оси Jω, одинаковых для двух ВРК упоров винтов Tv, коэффициента усиления kδ и постоянной времени Tδ привода ВРК; значения постоянных задающих воздействий и исходных данных: заданной угловой скорости ω* судна относительно его центра масс; свободного параметра Tu, имеющего смысл постоянной времени и предназначенного для регулирования быстродействия переходного процесса по угловой скорости, шага h дискретности по времени при расчете управления v, подаваемого на приводы ВРК. Способ приведения судна к заданной угловой скорости и ее удержания изображен на схеме рис. 1, на котором показаны: блок 1 - задающее воздействие ω* и выбираемые параметры Tu, h; блок 2 -расчет управляющего воздействия на приводы ВРК в дискретные моменты времени с шагом h, в котором используются значения параметров судна L, Jω„ Tv, kδ, Tδ и сигналы обратных связей ω, dω/dt, δ согласно выражениям, приведенным ниже; блок 3 - судно как объект управления с входом в виде управляющего воздействия на приводы ВРК v, выходом ω, dω/dt, δ и параметрами L, Jω,, Tv, kδ, Тδ.
Значения управляющего воздействия v, одного и того же для каждого из приводов ВРК, вычисляются с шагом h дискретности по времени. Предполагается, что динамика приводов описывается инерционным звеном первого порядка с коэффициентом усиления kδ и постоянной времени Tδ. Выражение для управляющего воздействия имеет вид:
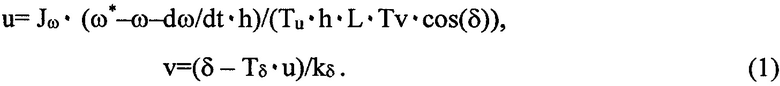
При получении (1) не производились какие-либо упрощения исходной нелинейной модели, что является новым элементом в сравнении с другими методами управления угловой скоростью и курсом судна. Как видно, в способе используются обратные связи по угловой скорости, угловому ускорению, а также углу поворота ВРК. Используются также массо-габаритные и тяговые характеристики судна в виде его длины и упора винта одной ВРК, а также косвенно, через присоединенный момент инерции, водоизмещение судна. В случае, когда угловые ускорения малы, можно использовать упрощенный способ, отличающийся от (1) отсутствием члена с ускорением, т.е.:
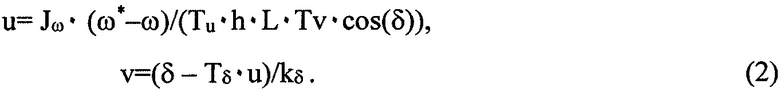
Проверка способов (1) и (2) на модели маломерного судна-катамарана с весовым водоизмещением (массой) 155000 кг, параметрами L=22,3 м, Tv=22400 н, 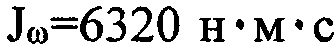 , kδ=1, Tδ=1 с, Tu=0,1 с, h=0,063 с, разнообразными задающими воздействиями ω* показала [13], что как (1), так и (2), успешно справляются с задачами выхода на заданные значения угловой скорости с очень высокой точностью (до одного процента). При этом в усложненном способе (1) переходный процесс по угловому ускорению имеет существенно меньшую колебательность по сравнению со случаем использования упрощенного способа (2). В то же время переходные процессы по скорости при этом практически одинаковые.
, kδ=1, Tδ=1 с, Tu=0,1 с, h=0,063 с, разнообразными задающими воздействиями ω* показала [13], что как (1), так и (2), успешно справляются с задачами выхода на заданные значения угловой скорости с очень высокой точностью (до одного процента). При этом в усложненном способе (1) переходный процесс по угловому ускорению имеет существенно меньшую колебательность по сравнению со случаем использования упрощенного способа (2). В то же время переходные процессы по скорости при этом практически одинаковые.
Особую роль играет параметр Tu, с помощью которого можно регулировать в широких пределах длительность переходного процесса по угловой скорости. Например, для достижения судном-катамараном угловой скорости ω*=0,008с-1 при значении Tu=0,02 получена длительность переходного процесса около 20с, а при значении Tu=1 указанная длительность получилась около 300с. Из (1) и (2) также видна еще одна особенность предложенного способа: независимость ошибки регулирования от погрешностей значений массо-габаритных и тяговых характеристик судна ввиду того, что все указанные параметры, кроме параметров привода, образуют один коэффициент 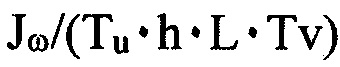 . Поэтому все ошибки в задании момента инерции, длины судна, значения упора, шага дискретности, приведут лишь к изменению времени переходного процесса и не повлияют на установившуюся ошибку регулирования. Устойчивость процессов здесь оценить затруднительно ввиду нелинейности системы, а также используемого метода управления. В данном методе вместо понятия «устойчивость» целесообразно опираться на «достижимость цели управления». Эта достижимость зависит от рационального выбора величин задающего воздействия ω*, времени работы системы и параметра Tu: при неудачном их выборе, когда судно не может за заданное время достичь заданной угловой скорости, процесс «срывается» в том смысле, что цель управления не достигается.
. Поэтому все ошибки в задании момента инерции, длины судна, значения упора, шага дискретности, приведут лишь к изменению времени переходного процесса и не повлияют на установившуюся ошибку регулирования. Устойчивость процессов здесь оценить затруднительно ввиду нелинейности системы, а также используемого метода управления. В данном методе вместо понятия «устойчивость» целесообразно опираться на «достижимость цели управления». Эта достижимость зависит от рационального выбора величин задающего воздействия ω*, времени работы системы и параметра Tu: при неудачном их выборе, когда судно не может за заданное время достичь заданной угловой скорости, процесс «срывается» в том смысле, что цель управления не достигается.
В упрощенном способе (2), в случае безынерционного привода управление имеет вид:
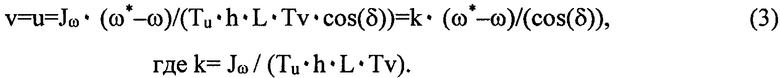
Если считать при этом управляющим сигналом угол поворота ВРК δ, то:

т.е. интеграл от сигнала, равного ошибке регулирования, деленного на косинус угла поворота ВРК, с постоянным коэффициентом k. При малых углах δ имеем cos(δ)≈1, в результате чего получаем интегральный регулятор в прямой цепи, на который подается ошибка регулирования. Таким образом, предлагаемый способ представляет собой вариант интегрального регулятора в прямой цепи, отличающегося от известных схем тем, что для больших отклонений |δ|<90° сигнал на входе интегратора делится на косинус δ.
Соответствующая схема приведена на рис. 2.
Изобретение получено в рамках исследований, выполненных при финансовой поддержке государства в лице Минобрнауки России (уникальный идентификатор проекта RFMEFI57817X0259).
Литература:
1. Вагущенко Л.Л., Цымбал Н.Н. Системы автоматического управления движением судна. М.: ТрансЛит, 2007. 376 с.
2. Система автоматического управления судном [Текст] пат. 2248914 Рос. Федерация: МПК В63Н 025/04 / Клячко Л.М., Острецов Г.Э., Памухин С.Г.; заявитель и патентообладатель Учреждение Российской академии наук Институт проблем управления им. В.А. Трапезникова РАН (RU). - №2004106058/11; заявл. 01.03.2004; опубл. 27.03.2005, Бюл. №9. - 7 с.: ил.
3. Способ автоматического управления движением судна [Текст] пат. 2292289 Рос. Федерация: МПК В63Н 25/04, G05D 1/00 / Острецов Г.Э., Клячко Л.М., Белогорцева М.В.; заявитель и патентообладатель Учреждение Российской академии наук Институт проблем управления им. В.А. Трапезникова РАН (RU). - №2005123073/11; заявл. 20.07.2005; опубл. 27.01.2007, Бюл. №3. - 7 с.: ил.
4. Способ управления движением судна по заданной траектории [Текст] пат. 2465169 Рос. Федерация: МПК В63Н 25/04/ Дорри М.Х., Острецов Г.Э., Рощин А.А.; заявитель и патентообладатель Учреждение Российской академии наук Институт проблем управления им. В.А. Трапезникова РАН (RU). - №2011115525/11; заявл. 21.04.2011; опубл. 27.10.2012, Бюл. №30. - 9 с.: ил.
5. Способ управления движением судна по заданной траектории [Текст] пат. 2483973 Рос. Федерация: МПК В63Н 25/04/ Острецов Г.Э., Клячко Л.М., Памухин С.Г.; заявитель и патентообладатель Учреждение Российской академии наук Институт проблем управления им. В.А. Трапезникова РАН (RU). - №2011131927/11; заявл. 29.07.2011; опубл. 10.06.2013, Бюл. №4. - 7 с.: ил.
6. Aguiar, A.P., and Pascoal, A.M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents, 41st IEEE Conference on Decision and Control. Proceedings (Cat. No. 02CH37375), v 2, 2002, p 2105-2110.
7. Yacong Zhao, Haibin Huang and Yufei Zhuang. The Heading Control of POD-Driven Ship Using Adaptive Integrator Backstepping // © Springer-Verlag Berlin Heidelberg 2016 B. Huang and Y. Yao (eds.), Proceedings of the 5th International Conference on Electrical Engineering and Automatic Control, Lecture Notes in Electrical Engineering 367, DOI 10.1007/978-3-662-48768-6_20.P.173-179.
8. Кориков A.M. Интеллектуальное управление в технических системах // Научный вестник НГТУ, 2014. №1(54). С. 18-26.
9. Anna Witkowska, Roman Smierzchalski. Designing a ship course controller by applying the adaptive backstepping method // Int. J. Appl. Math. Comput. Sci., 2012, Vol. 22, No. 4, P. 985-997.
10. S. Sutulo, L. Moreira, C. Guedes Soares. Mathematical models for ship path prediction in manoeuvring simulation systems // Ocean Engineering 29 (2002) 1-19. P. 1-19.
11. Yasuo Yoshimura. Mathematical Model for Manoeuvring Ship Motion (MMG Model) // Workshop on Mathematical Models for Operations involving Ship-Ship Interaction August 2005 Tokyo. P. 2-6.
12. Hashem Ashrafiuon, Kenneth R. Muske. Sliding Mode Tracking Control of Surface Vessels // 2008 American Control Conference Westin Seattle Hotel, Seattle, Washington, USA. June 11-13, 2008. P. 557-561.
13. Шушляпин E.A., Карапетьян B.A., Безуглая A.E., Афонина А.А. Нелинейные регуляторы для удержания судна на заданной траектории при «сильных» маневрах // Труды СПИИРАН. 2017. - СПб: СПИИРАН, Вып. 53. - С. 178-200.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УПРАВЛЕНИЯ ПРОГРАММНЫМИ ДВИЖЕНИЯМИ СУДНА ПО ТРАЕКТОРИИ | 2015 |
|
RU2596202C1 |
| Способ отслеживания запланированного маршрута морского подвижного объекта | 2018 |
|
RU2703338C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ ПРОВОДКИ СУДНА | 2021 |
|
RU2759068C1 |
| СИСТЕМА ИДЕНТИФИКАЦИИ ГИДРОДИНАМИЧЕСКИХ КОЭФФИЦИЕНТОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДВИЖЕНИЯ СУДНА | 2013 |
|
RU2535777C1 |
| СПОСОБ НАСТРОЙКИ СИСТЕМЫ УПРАВЛЕНИЯ СУДНОМ ПО КУРСУ | 2024 |
|
RU2828164C1 |
| СПОСОБ ПРОВОДКИ, ШВАРТОВКИ И ОТШВАРТОВКИ МОРСКОГО ГРУЗОВОГО СУДНА В АВТОНОМНОМ РЕЖИМЕ И СПОСОБ РАБОТЫ ЦИФРОВОЙ ИНСТРУМЕНТАЛЬНОЙ ПЛАТФОРМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ГРУППЫ АВТОНОМНЫХ СУДОВ-БУКСИРОВ В ПОРТОВОЙ АКВАТОРИИ | 2023 |
|
RU2809129C1 |
| АППАРАТУРА УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОРАБЛЯ ПРИ ВОЛНЕНИИ | 2009 |
|
RU2392181C1 |
| СПОСОБ ОТКАЗОБЕЗОПАСНОГО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ КОРАБЛЯ | 2010 |
|
RU2432297C1 |
| СИСТЕМА КООРДИНИРОВАННОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ СУДНА В РЕЖИМАХ АВТОМАТИЧЕСКОГО И ДИСТАНЦИОННОГО УПРАВЛЕНИЯ | 2020 |
|
RU2741669C1 |
| ОТКАЗОУСТОЙЧИВАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ДВИЖЕНИЕМ СУДНА | 2013 |
|
RU2532000C1 |
Изобретение относится к области судовождения, к автоматическому управлению движением судна-катамарана с двумя винторулевыми колонками (ВРК) при осуществлении им «сильных» маневров. Используют сигналы: текущих значений угловой скорости ω и ускорения dω/dt судна в горизонтальной плоскости относительно центра масс, одинакового для двух ВРК угла поворота δ; постоянные значения: длины судна L, присоединенного момента инерции судна относительно вертикальной оси Jω, одинаковых для двух ВРК упоров винтов Tv, коэффициента усиления kδ и постоянной времени Tδ привода ВРК; значения постоянных задающих воздействий и исходных данных: заданной угловой скорости ω* судна относительно его центра масс; свободного параметра Tu, имеющего смысл постоянной времени и предназначенного для регулирования быстродействия переходного процесса по угловой скорости, шага h дискретности по времени при расчете управления v, подаваемого одновременно на оба привода ВРК. Управляющее воздействие v рассчитывают через фиксированные интервалы времени длительностью h методом терминального управления нелинейными системами - методом конечного состояния. Достигается повышение точности работы системы управления. 2 ил.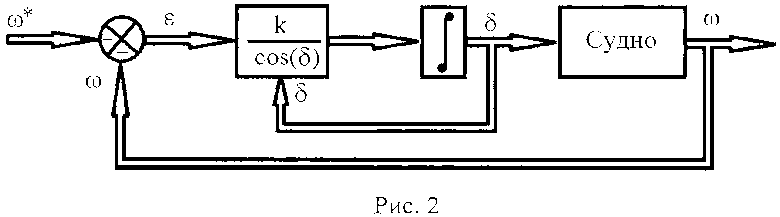
Способ автоматического управления «сильными» маневрами судна-катамарана с использованием сигналов от датчиков угловой скорости ω и ускорения dω/dt при повороте судна-катамарана с двумя поворачивающимися на один и тот же угол δ винторулевыми колонками (ВРК) вокруг центра масс, а также сигнала от угла δ, отличающийся от известных способов тем, что при его разработке использована нелинейная динамическая модель судна седьмого порядка без последующих упрощений и «метод конечного состояния» для терминального управления нелинейными системами, с помощью которых получен управляющий сигнал в виде явной зависимости от массогабаритных и тяговых характеристик судна 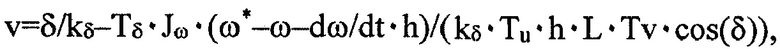 где v - управляющий сигнал на входах приводов ВРК, kδ, Tδ - коэффициент усиления и постоянная времени привода ВРК, Jω - присоединенный момент инерции судна вокруг вертикальной оси, ω* - заданное значение угловой скорости, Tu - параметр для регулировки быстродействия переходного процесса по ω, h - шаг дискретности по времени при расчете v, L - длина судна, Tv - постоянный упор винта одной ВРК, а также упрощенное управление для случая близкого к нулю углового ускорения
где v - управляющий сигнал на входах приводов ВРК, kδ, Tδ - коэффициент усиления и постоянная времени привода ВРК, Jω - присоединенный момент инерции судна вокруг вертикальной оси, ω* - заданное значение угловой скорости, Tu - параметр для регулировки быстродействия переходного процесса по ω, h - шаг дискретности по времени при расчете v, L - длина судна, Tv - постоянный упор винта одной ВРК, а также упрощенное управление для случая близкого к нулю углового ускорения 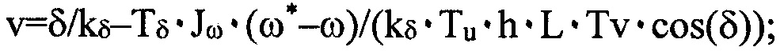 для управляющего сигнала в виде угла поворота ВРК δ в предположении безынерционности привода способ имеет вид выражения
для управляющего сигнала в виде угла поворота ВРК δ в предположении безынерционности привода способ имеет вид выражения 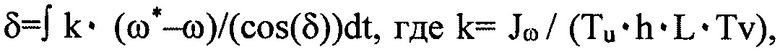 который при малых углах δ, когда cos(δ)≈1, представляет собой интегральный регулятор в прямой цепи контура управления, а при больших углах, характерных для «сильных» маневров, видоизмененный интегральный регулятор с нелинейной обратной связью от угла δ.
который при малых углах δ, когда cos(δ)≈1, представляет собой интегральный регулятор в прямой цепи контура управления, а при больших углах, характерных для «сильных» маневров, видоизмененный интегральный регулятор с нелинейной обратной связью от угла δ.
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ СУДНА ПО ЗАДАННОЙ ТРАЕКТОРИИ | 2011 |
|
RU2465169C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ СУДНА ПО ЗАДАННОЙ ТРАЕКТОРИИ | 2011 |
|
RU2483973C2 |
| СИСТЕМА УПРАВЛЕНИЯ | 2011 |
|
RU2527570C2 |
| 0 |
|
SU157389A1 | |
| US 9857794 В1, 02.01.2018 | |||
| СПОСОБ ДВИЖЕНИЯ НА ВОДЕ И СКОРОСТНОЕ СУДНО ДЛЯ ДВИЖЕНИЯ НА ВОДЕ НА ВЕКТОРАХ УПОРОВ ВОДНЫХ ДВИЖИТЕЛЕЙ (ВАРИАНТЫ) | 2007 |
|
RU2364544C2 |
Авторы
Даты
2019-07-03—Публикация
2018-09-11—Подача