Заявляемое изобретение относится к области приборостроения и может быть использовано при выставке бесплатформенных инерциальных навигационных систем (БИНС) управляемого аппарата (УА).
В изобретении представлен способ идентификации углов рассогласования БИНС УА и ИНС самолета-носителя методом наименьших квадратов (МНК) в частотной области, который выполняет совместную обработку всех накопленных данных на выбранном участке маневра носителя с подвеской.
Способ устойчив и менее чувствителен к характеру маневра самолета-носителя и к погрешностям измерений, поскольку работает на нижних гармониках переходных процессов. Предназначен для разового применения и не требует решения с постоянной частотой. Выполнение идентификации осуществляется по следующей схеме:
-по команде «начало маневра» начинают накапливаться измерения датчиков ИНС и БИНС;
-по окончании маневра вычислитель БИНС выполняет расчет углов подвески;
- контроль правильности оценок выполняется как в частотной области, так и во временной области представления переходных процессов, о результатах контроля выдается сообщение.
Существует Способ определения углового положения управляемого аппарата, подвешенного к самолету-носителю [1].
Способ включает в себя предварительную обработку сигналов, соответствующих угловым скоростям, измеренным трехкомпонентными датчиками угловых скоростей (ДУС), установленными на УА и самолете-носителе (СН), на маневре СН типа «змейка», основанную на применении метода фильтрации Калмана. При поступлении в вычислитель УА соответствующей команды СН выполняет маневр типа «змейка» с угловой скоростью 10-15 град/сек, при этом начинается выполнение согласования векторов измерений угловых скоростей ДУС УА и ДУС СН, по которому минимизируется взвешенная среднеквадратическая ошибка рассогласования измерений ДУС УА относительно измерений ДУС СН. По окончательной матрице поворота вычисляются результирующие оценки углов рассогласования между осями ДУС УА и ДУС СН, которые и определяют ориентацию изделия относительно носителя.
Недостатком является слишком жесткое требование к параметрам выполнения маневра СН для создания угловой скорости поворота 10-15 град/сек. СН необходимо создать большую перегрузку с большим креном. Для больших самолетов-носителей данную фигуру выполнить сложно. Второй недостаток связан с необходимостью применения рекуррентного фильтра Калмана большой размерности для формирования приемлемых по точности оценок углов подвески по истечении достаточно длительного времени.
Целью предлагаемого изобретения является одноразовое определение с требуемой точностью углов рассогласования осей связанных систем координат УА и СН в полете, которые используются для начальной выставки БИНС УА при отсутствии жестких требований к параметрам маневра СН.
Поставленная цель достигается за счет того, что согласно заявляемому способу идентификации углов рассогласования БИНС УА и ИНС СН, использующему выходные сигналы БИНС УА, соответствующие угловым скоростям и выходные сигналы ИНС СН, соответствующие угловым скоростям, причем измерение угловых скоростей производят с использованием специального маневра СН, дополнительно по команде «начало маневра» начинают накапливать измерения ИНС СН и БИНС УА, вводят матрицу функций чувствительности оценок изображений угловых скоростей БИНС УА к малым вариациям углов подвески, составляют модель связи угловой скорости ИНС СН ω1(t) и угловой скорости БИНС УА ω2(t), вводят аТ=[ϑ γ ψ] - вектор углов подвески, по окончании маневра вычислитель БИНС УА один раз выполняет расчет оценок углов подвески с использованием итерационного метода определения функций чувствительности изображений угловых скоростей в частотной области к вариациям искомых углов подвески, при этом используют преобразование Фурье для перевода угловых скоростей в частотную область, расчет изображения для одной частоты выполняют с учетом приведения к действительному виду по методу Хартли, вектор углов подвески оценивают итерационно частотным методом наименьших квадратов, контролируют правильность оценок как в частотной области, так и в во временной области представления переходных процессов, о результатах контроля выдается сообщение.
Сущность изобретения поясняется графическими рисунками, представляющими результаты моделирования работы предлагаемого способа при различных маневрах.
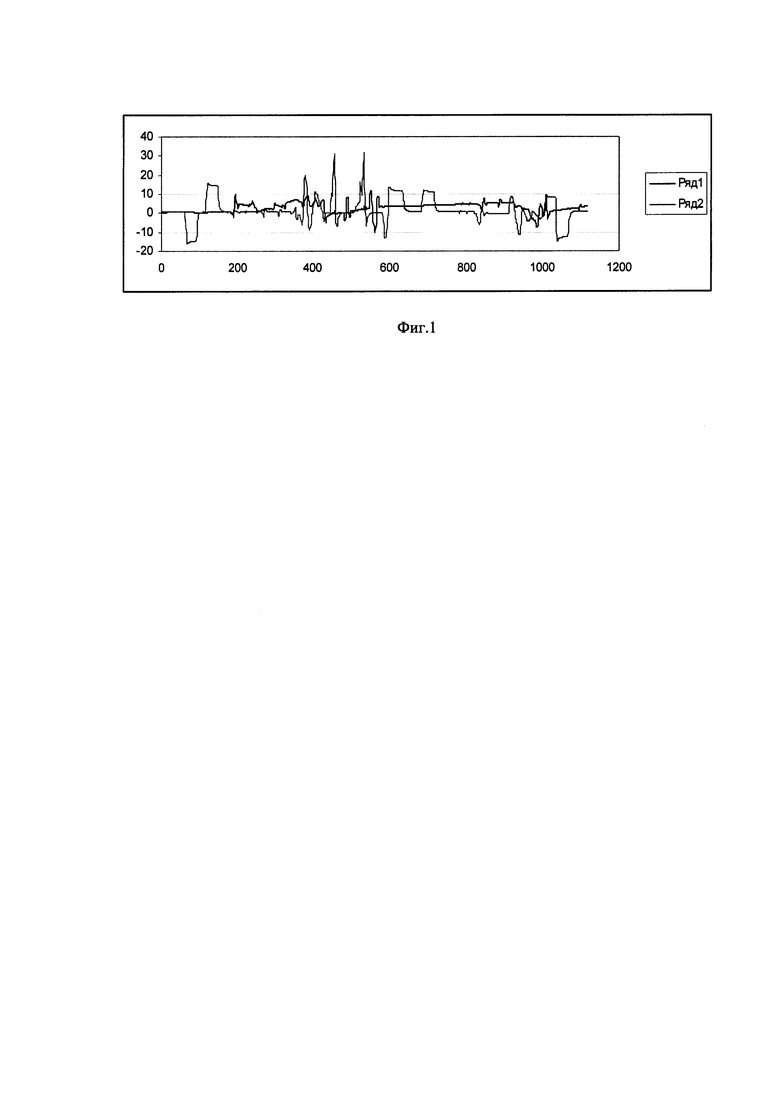
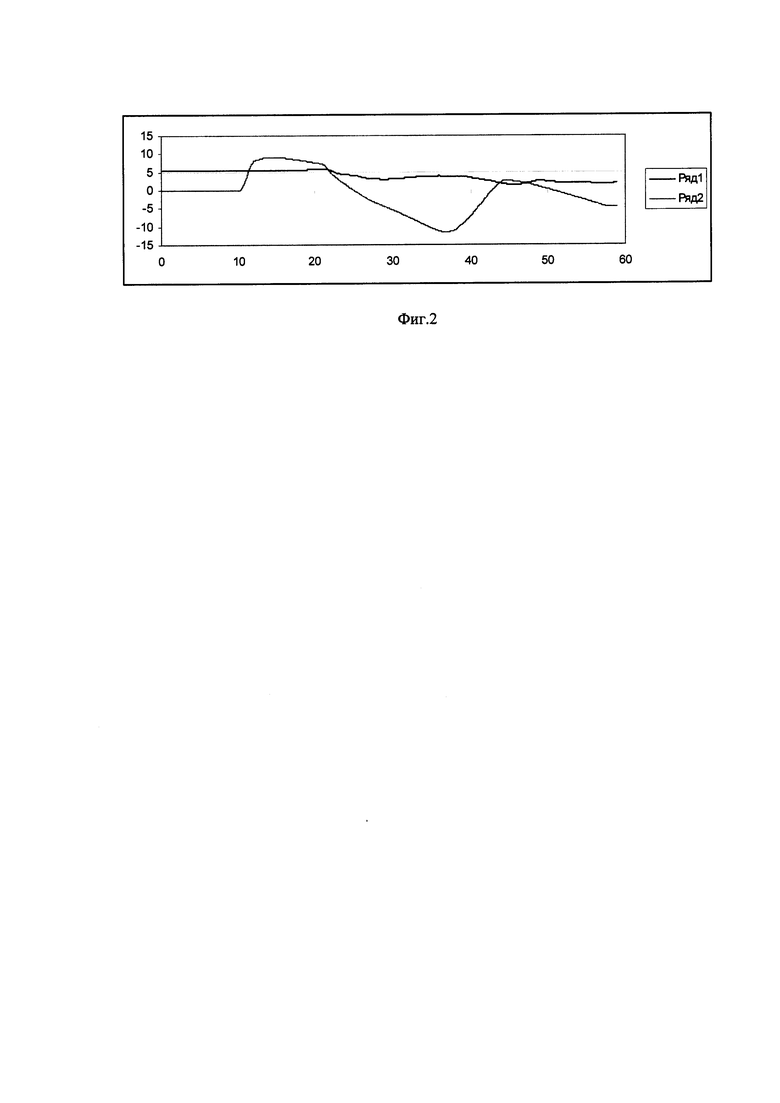
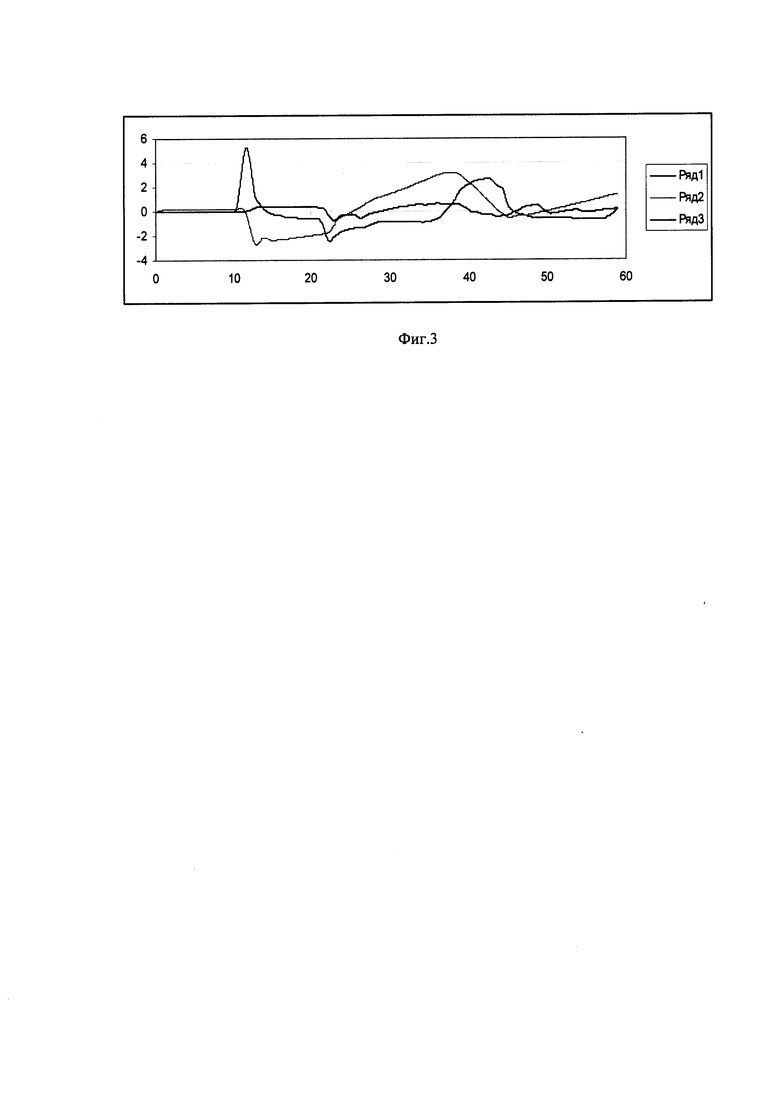
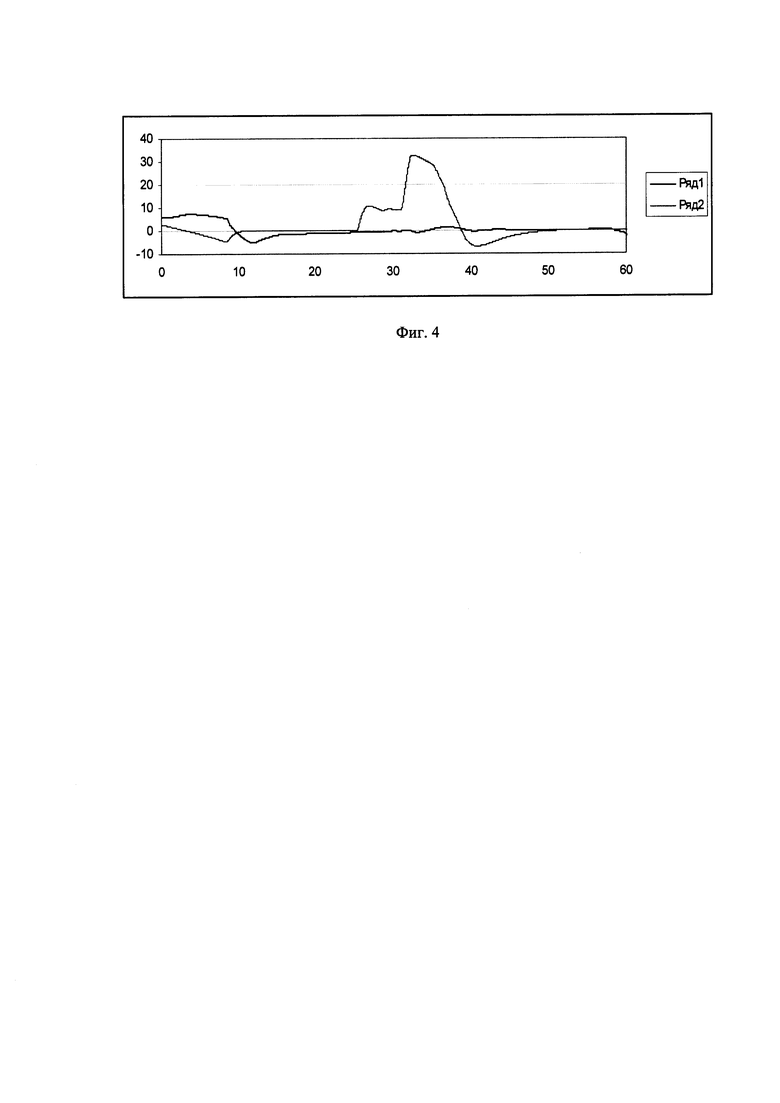
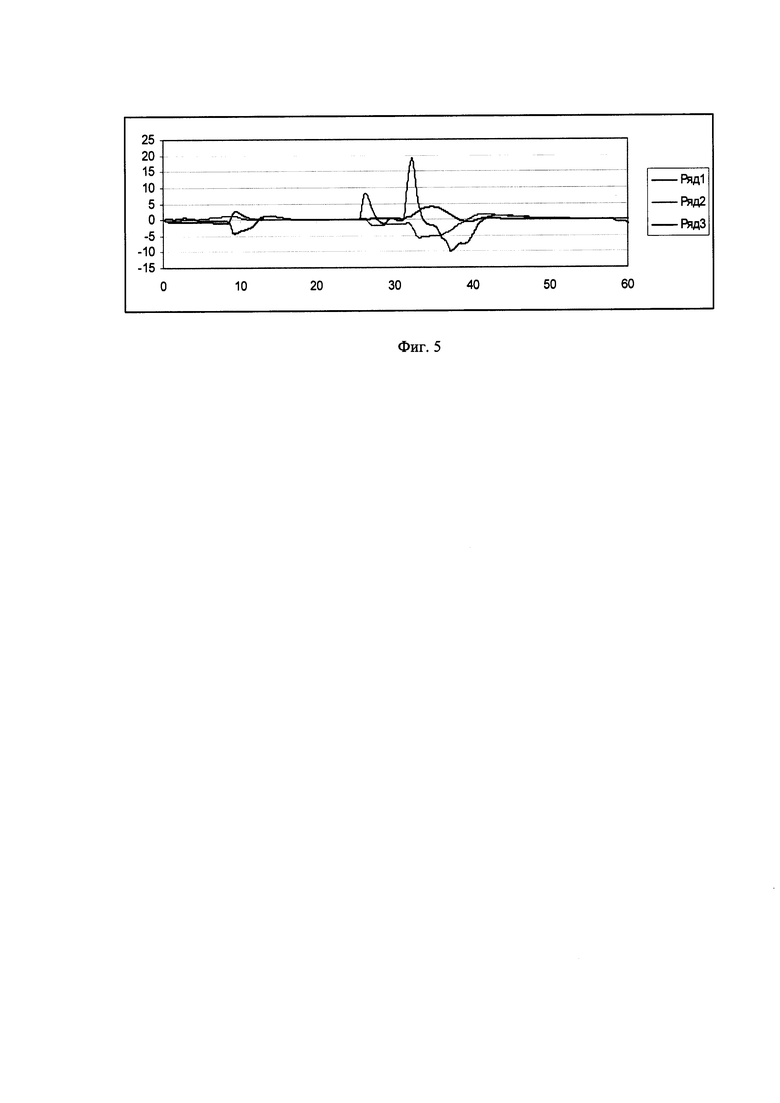
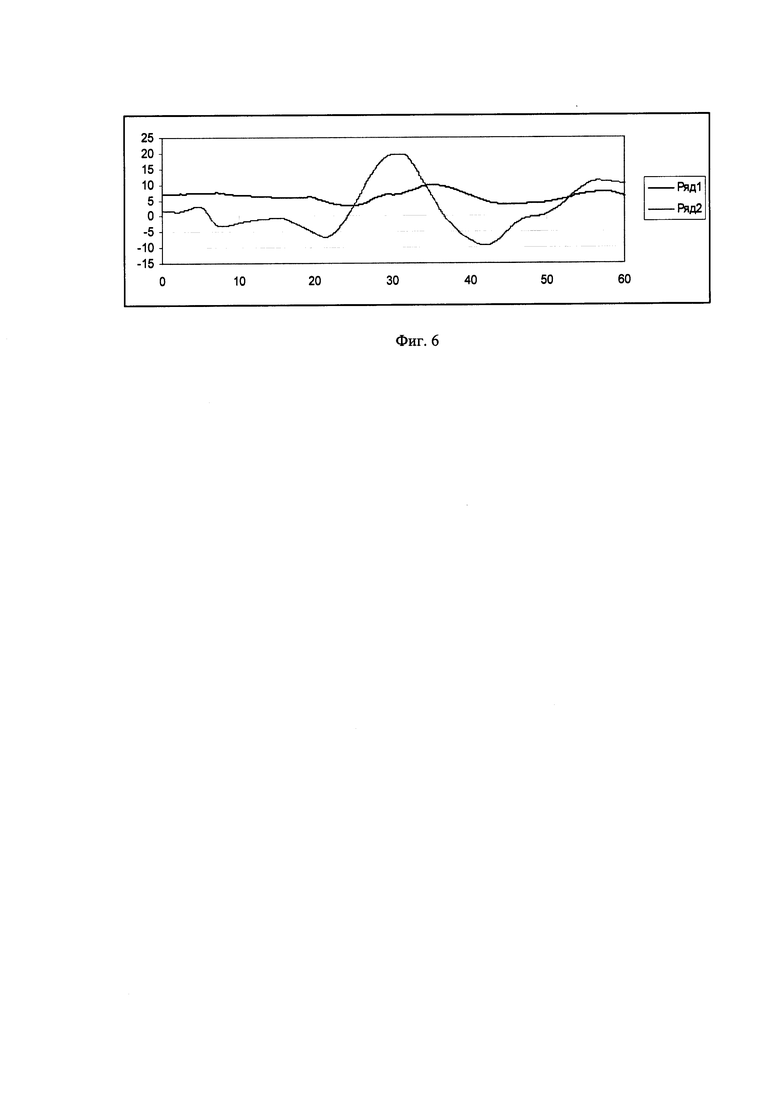
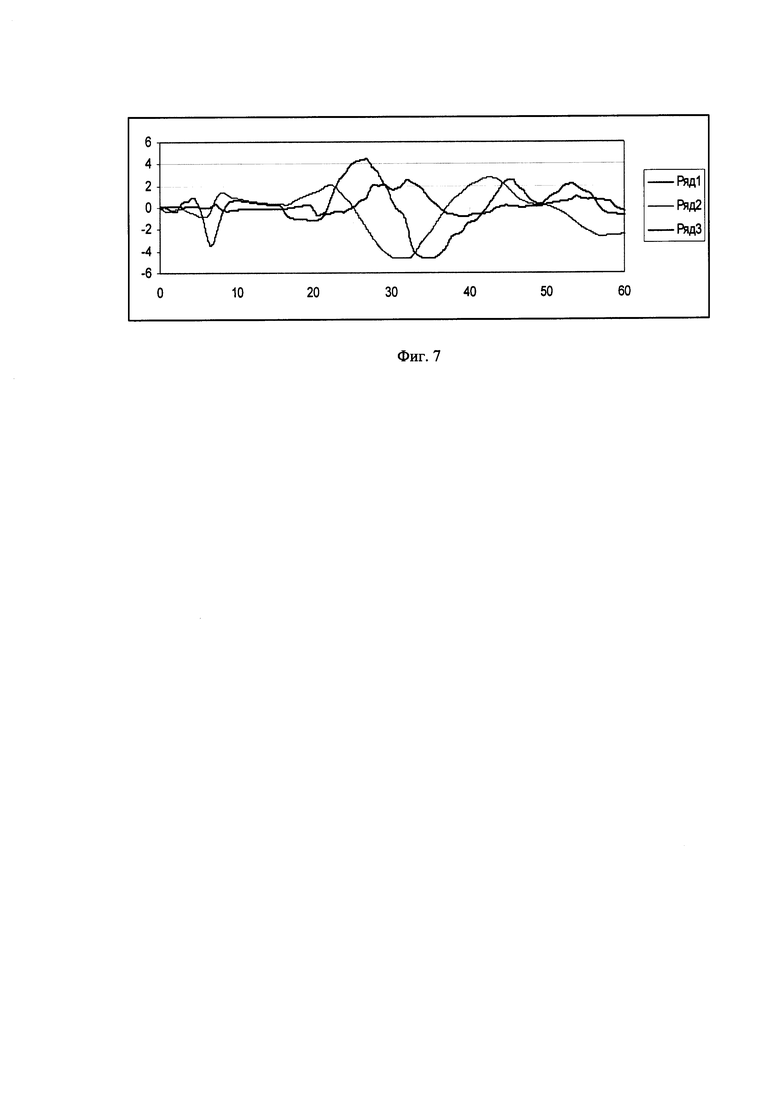
На Фиг. 1 приведены данные полета по углам тангажа и крена: 1-тангаж; 2-крен; на Фиг. 2 - данные по углам на участке 1:1 - тангаж; 2-крен; на Фиг. 3 - данные по угловым скоростям на участке 1:1-ωх; 2-ωу; 3-ωz; Фиг. 4. - демонстрирует данные полета на участке 2:1 - тангаж; 2 - крен; Фиг. 5 - данные на участке 2:1-ωх; 2-ωу; 3-ωz; Фиг. 6. - данные на участке 3:1 - тангаж; 2 - крен; Фиг. 7 - данные на участке 3: 1-ωх; 2-ωу; 3-ωz.
В способе используется метод согласования векторов угловых скоростей носителя и подвески. Жестких требования на выполнение маневра СН не накладывается, однако желательно выполнение такого маневра, при котором имеют место переходные процессы по всем трем проекциям угловой скорости. При этом изменение угловых скоростей не должно быть синфазным. При правильном развороте по крену это требование для угловых скоростей ωх, ωу удовлетворяется само собой, но переходный процесс по тангажу и соответственно угловую скорость ωz надо создавать дополнительно.
Необходимо, чтобы в течение этого времени маневр имел вид разворотов в одну и другую сторону с креном 10-15 градусов при изменении тангажа с амплитудой 5-10 градусов так, чтобы амплитуда каждой из трех создаваемых проекций угловой скорости была не менее нескольких единиц градусов в секунду. Время маневра не менее 15 секунд.
В условиях имеющейся недостаточности располагаемых полетных данных целесообразно ориентироваться на метод, называемый «Частотный МНК». Идентификация по нижней части спектра процессов угловых скоростей допускает наличие погрешности измерений, пониженную частоту регистрации и менее чувствительна к запаздыванию.
Предлагается использовать метод функций чувствительности изображений процессов изменения угловых скоростей в частотной области к вариациям искомых углов подвески. При этом алгоритм идентификации, в отличие от фильтра Калмана, является не рекуррентным, а итерационным и работает не последовательно во времени течения процессов, а применяется один раз сразу для всего исследуемого участка наблюдений и накопленной на этом участке информации.
Соотношения метода следующие:
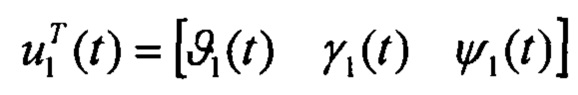 - вектор углов ИНС СН, по которому с помощью интерполяции, дифференцирования и кинематических соотношений вычисляется вектор угловых скоростей ИНС ЛА ω1(t).
- вектор углов ИНС СН, по которому с помощью интерполяции, дифференцирования и кинематических соотношений вычисляется вектор угловых скоростей ИНС ЛА ω1(t).
ω1(t)=A(ϑ, γ, ψ)ω2(t) - модель связи угловой скорости ИНС СН ω1(t) и угловой скорости БИНС УА ω2(t).
ϑ, γ, ψ - искомые углы БИНС УА,
A(ϑ, γ, ψ) - матрица поворота, aT=[ϑ γ ψ] - вектор углов подвески.
Вектор углов подвески уточняется итерационно, начальное значение нулевое:

k - номер итерации; 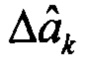 - вектор приращений, вычисляется по МНК:
- вектор приращений, вычисляется по МНК:

где: 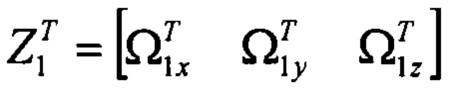 - вектор изображений угловых скоростей ИНС СН;
- вектор изображений угловых скоростей ИНС СН;
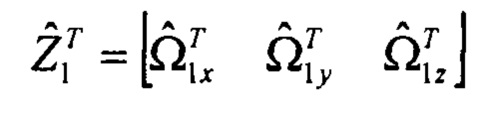 - вектор оценок изображений угловых скоростей ИНС СН, вычисляемый по угловым скоростям ω2(t) БИНС УА с учетом оценки матрицы поворота A(ϑ, γ, ψ) подвески в соответствии с моделью:
- вектор оценок изображений угловых скоростей ИНС СН, вычисляемый по угловым скоростям ω2(t) БИНС УА с учетом оценки матрицы поворота A(ϑ, γ, ψ) подвески в соответствии с моделью:


ϕ - матрица функций чувствительности оценок изображений угловых скоростей ИНС ЛА к малым вариациям углов подвески δα. Матрица определяется численно.
Для расчета изображений угловых скоростей задается множество расчетных точек по частоте {fi} с шагом разрешающей способности финитного преобразования Фурье:

где Т - длительность процессов.
Расчет изображения для одной частоты выполняется с учетом приведения угловой скорости к действительному виду по методу Хартли:

где: F[ω(t)] - финитное преобразование Фурье на отрезке времени наблюдения t∈[0,T]
Результаты моделирования
На фиг. 1 представлены процессы изменения крена и тангажа самолета в течение всего полета.
Маневр для определения углов подвески не должен быть длительным. Из процессов всего полета сначала выбрано 3 участка, продолжительностью 60 секунд, которые содержат относительно короткие переходные процессы, пригодные для идентификации углов подвески. Процессы для трех участков по 60 секунд представлены на фиг. 2-7.
Из фиг. 2, 3 следует, что маневр плавный, при этом движение по тангажу незначительно и угловая скорость ωz менее одного градуса в секунду. При больших шумах она будет плохо заметна.
Из фиг. 4, 5 следует, что маневр более короткий и резкий. Угловая скорость ωz больше, но ее вторая часть переходного процесса синфазна с изменением угловой скорости ωу, что нежелательно.
Из фиг. 6, 7 следует, что продолжительность и интенсивность маневра являются как бы средними между маневрами на участках 1 и 2. Амплитуды угловых скоростей примерно соизмеримы.
Из всех трех вариантов второй имеет наиболее короткие переходные процессы, время которых представляется реальным для применения. По результатам анализа следует, что движение по крену необходимо выполнить симметрично в одну и другую сторону. Для идентификации из представленных участков длительностью 60 секунд выделялись более короткие, длительностью 15-20-30 секунд, содержащие переходные процессы по угловым скоростям с наибольшей амплитудой и имитировались измерения ДУС подвески с углами рассогласования осей БИНС относительно осей ИНС 10 градусов по каждому из трех углов.
Моделирование показало, что при постоянном запаздывании и малом уровне шумов имеют место примерно одинаковые оценки углов подвески для всех трех вариантов с погрешностью порядка 0.3-0.5 градуса.
Техническим результатом предложенного изобретения является то, что предложенный способ не предъявляет жестких требований к параметрам выполнения маневра СН. Процесс идентификации устойчив и менее чувствителен к погрешностям измерений, поскольку работает на нижних гармониках переходных процессов, и не требует решения с постоянной частотой. Позволяет обеспечить дополнительный контроль результатов согласования путем сравнения угловых скоростей АУ и СН с учетом полученных оценок.
Литература
1. Патент RU 2553776. Способ определения углового положения управляемого аппарата, подвешенного к самолету-носителю. Заец В.Ф., Кулабухов B.C., Качалов Б.О., Туктарев Н.А. Опубл. 20.06.2015, Бюлл.№17.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ выставки БИНС ЛА корабельного базирования и устройство для его осуществления | 2016 |
|
RU2635398C2 |
| Способ коррекции углов ориентации БИНС на скользящем интервале | 2022 |
|
RU2790076C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОГО ПОЛОЖЕНИЯ УПРАВЛЯЕМОГО АППАРАТА, ПОДВЕШЕННОГО К САМОЛЕТУ-НОСИТЕЛЮ | 2014 |
|
RU2553776C1 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2635820C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2264598C1 |
| СПОСОБ ИЗМЕРЕНИЯ УГЛОВЫХ ПОЛОЖЕНИЙ ЛЕТАТЕЛЬНОГО АППАРАТА | 2004 |
|
RU2256154C1 |
| СПОСОБ КОРРЕКЦИИ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ | 2014 |
|
RU2564380C1 |
| СИСТЕМА ФОРМИРОВАНИЯ РЕЗЕРВНОЙ ИНФОРМАЦИИ О ПРОСТРАНСТВЕННОМ ПОЛОЖЕНИИ ЛЕТАТЕЛЬНОГО АППАРАТА | 2006 |
|
RU2324623C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2014 |
|
RU2564379C1 |
| СПОСОБ ОЦЕНКИ ОШИБОК И КОНТРОЛЯ ДАТЧИКОВ ПЕРВИЧНОЙ ИНФОРМАЦИИ В СОСТАВЕ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ В НАЗЕМНЫХ УСЛОВИЯХ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2012 |
|
RU2537513C2 |
Изобретение относится к области приборостроения и может быть использовано при выставке бесплатформенных инерциальных навигационных систем (БИНС) управляемого аппарата (УА). Способ идентификации углов рассогласования БИНС УА и ИНС самолета-носителя (СН), использующий угловые скорости выходных сигналов БИНС УА и ИНС СН, измерение угловых скоростей производят при выполнении специального маневра СН. При этом дополнительно по команде «начало маневра» начинают накапливать измерения датчиков ИНС и БИНС, вводят матрицу функций чувствительности, составляют модель связи угловой скорости ИНС ЛА и угловой скорости БИНС подвески, вводят вектор углов подвески, по окончании маневра вычислитель БИНС выполняет расчет углов подвески. Для расчета используют итерационный метод функций чувствительности изображений процессов изменения угловых скоростей в частотной области к вариациям искомых углов подвески, при этом используют преобразование Фурье для перевода процессов в частотную область, расчет изображения для одной частоты выполняют с учетом приведения к действительному виду по методу Хартли. Вектор углов подвески оценивают один раз по окончании маневра с использованием итерационной процедуры частотного метода наименьших квадратов, контролируют правильность оценок углов подвески как в частотной области, так и в области времени представления переходных процессов, о результатах контроля выдается сообщение. Технический результат – обеспечение возможности одноразового определения с требуемой точностью углов рассогласования осей связанных систем координат УА и СН в полете. 7 ил. 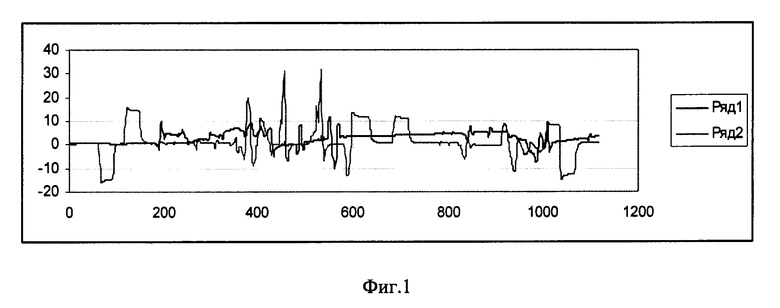
Способ идентификации углов рассогласования БИНС управляемого аппарата (УА) и ИНС самолета-носителя (СН), использующий угловые скорости выходных сигналов бесплатформенной инерциальной системы (БИНС) УА и ИНС СН, измерение угловых скоростей производят при выполнении специального маневра СН, отличающийся тем, что дополнительно по команде «начало маневра» начинают накапливать измерения датчиков ИНС и БИНС, вводят матрицу функций чувствительности, составляют модель связи угловой скорости ИНС ЛА ω1(t) и угловой скорости БИНС подвески ω2(t), вводят aT=[ϑ γ ψ] - вектор углов подвески, по окончании маневра вычислитель БИНС выполняет расчет углов подвески, для расчета используют итерационный метод функций чувствительности изображений процессов изменения угловых скоростей в частотной области к вариациям искомых углов подвески, при этом используют преобразование Фурье для перевода процессов в частотную область, расчет изображения для одной частоты выполняют с учетом приведения к действительному виду по методу Хартли, вектор углов подвески оценивают один раз по окончании маневра с использованием итерационной процедуры частотного метода наименьших квадратов, контролируют правильность оценок углов подвески как в частотной области, так и в области времени представления переходных процессов, о результатах контроля выдается сообщение.
| СПОСОБ ОПРЕДЕЛЕНИЯ УГЛОВОГО ПОЛОЖЕНИЯ УПРАВЛЯЕМОГО АППАРАТА, ПОДВЕШЕННОГО К САМОЛЕТУ-НОСИТЕЛЮ | 2014 |
|
RU2553776C1 |
| Способ определения углов пространственной ориентации | 2016 |
|
RU2713078C1 |
| ИНТЕГРИРОВАННАЯ БЕСПЛАТФОРМЕННАЯ СИСТЕМА НАВИГАЦИИ СРЕДНЕЙ ТОЧНОСТИ ДЛЯ БЕСПИЛОТНОГО ЛЕТАТЕЛЬНОГО АППАРАТА | 2013 |
|
RU2539140C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ИСТИННОГО КУРСА ПОДВИЖНОГО ОБЪЕКТА | 2017 |
|
RU2671937C1 |
| БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ КУРСОВЕРТИКАЛЬ | 2003 |
|
RU2249791C2 |
| US 7962285 B2, 14.06.2011. | |||
Авторы
Даты
2023-02-14—Публикация
2022-01-27—Подача