Изобретение относится к области обработки металлов давлением, а именно к способам оценки длины дуги контакта валка и полосы при продольной прокатке на гладкой бочке.
Известен способ определения параметров очага деформации при прокатке (SU 1319964 А1, Способ определения параметров очага деформации при прокатке. В.И. Вергелес, В.В. Китаненко, Н.Ф. Грицук, Ю.Е. Кулак). Способ позволяет измерить длину очага деформации. Нет данных об эффективности применения данного способа для определения длины дуги захвата.
Известен способ расчета длины дуги захвата при Мульти-РКУП-К (Фахретдинова Э.И. Разработка нового комбинированного процесса получения алюминиевых деформированных полуфабрикатов электротехнического назначения. Автореферат диссертации на соискание ученой степени кандидата технических наук. Красноярск, 2017, с. 13-14). Нет данных о возможности применения данного способа для оценки длины дуги захвата при продольной прокатке.
Известен способ определения длины дуги контакта при прокатке (SU 1319945 А1. Николаев В.А., Пилипенко С.С., Волков И.А., Копан Т.Н. Способ определения длины дуги контакта при прокатке). Способ не предполагает определение длины дуги контакта при асимметричной прокатке.
Известен способ расчета горизонтальной проекции дуги захвата (А.И. Целиков, А.Д. Томленов, В.И. Зюзин, А.В. Третьяков, Г.С. Никитин. Теория прокатки. Справочник. М., «Металлургия», 1982, с. 174). Способ позволяет определить горизонтальную проекцию длины дуги захвата, в том числе при разных диаметрах валков, но не определить численно длину самой дуги захвата. Неизвестно, возможно ли использовать данный способ для асимметричной продольной прокатки полосы на гладкой бочке, в том числе при разных скоростях вращения валков, в случае если центры валков не лежат на одной вертикальной прямой.
Известен способ компьютерного моделирования плоско-деформированного состояния в процессе холодной продольной прокатки листов из алюминия в программном комплексе DEFORM-2D (Каргин В.Р., Гречников Ф.В., Шляпугин А.Г. Моделирование процессов ОМД [Электронный ресурс]: электрон. учеб. пособие. М-во образования и науки РФ, Самар. гос. аэрокосм. ун-т им. С.П. Королева. Самара, 2013, с. 461-463). Данный способ наиболее близок к предлагаемому изобретению. Способ заключается в подготовке данных для проведения компьютерного моделирования процесса продольной прокатки на гладкой бочке, компьютерном моделировании процесса продольной прокатки на гладкой бочке с помощью вычислительной среды конечно-элементного анализа в двумерной постановке. По результатам проектирования выбирают данные с результатами проектирования, соответствующие результатам проектирования установившейся стадии прокатки. Определяют эпюры распределения скорости деформации, касательных напряжений и нормальных давлений по дуге захвата. Способ не позволяет определить длину дуги захвата (контакта).
Техническим результатом является повышение точности и эффективности способов и методик расчета энергосиловых параметров процесса прокатки, в том числе асимметричной, износа валков, упругой деформации валков, размеров геометрического очага деформации, для осуществления которых (способов и методик) необходимо использование величины дуги захвата.
Технический результат достигается тем, что определяют параметры исследуемого процесса продольной прокатки: диаметр валков, зазор между валками, скорость вращения валков, температура и размеры полосы перед прокаткой. После этого проводят стандартные испытания на растяжение образцов материала недеформированной полосы на испытательной машине для определения сопротивления деформации. Определенные значения параметров исследуемого процесса прокатки и результаты стандартных испытаний на растяжение образцов материала недеформированной заготовки на испытательной машине используют для проведения компьютерного моделирования исследуемого процесса продольной прокатки полосы в условиях плоского деформированного состояния с помощью вычислительной среды конечно-элементного анализа. При подготовке данных для конечно-элементного компьютерного моделирования процесса прокатки и позиционирования объектов модели вводят прямоугольную систему координат. За начало координат принимается точка, являющаяся пересечением вертикальной прямой, проходящей через центр верхнего валка и горизонтальной прямой, проходящей через середину полосы по толщине и параллельную верхнему и нижнему краю полосы. Ось ординат направлена вертикально вверх, ось абсцисс сонаправлена с направлением прокатки. По завершении конечно-элементного компьютерного моделирования исследуемого процесса продольной прокатки с помощью инструментария вычислительной среды конечно-элементного анализа на установившейся стадии прокатки отображают область контакта полосы с выбранным валком. Определяют координаты по оси абсцисс точек, находящихся в области контакта и имеющих наибольшую и наименьшую координату по оси абсцисс среди всех точек области контакта полосы и выбранного валка. Также определяют координаты центра выбранного валка. В среде автоматизированного компьютерного проектирования создают плоский чертеж. В этом чертеже создают точки с координатами, соответствующими координатам точек с наибольшей и наименьшей координатами по оси абсцисс среди точек контакта полосы и выбранного валка, а также создают точку, являющуюся центром выбранного валка. С помощью инструментария среды автоматизированного компьютерного проектирования в созданном чертеже строят дугу через три точки, а именно через точку, являющуюся центром выбранного валка, которую принимают за центр дуги, и две точки, соответствующие точкам с наибольшей и наименьшей координатами по оси абсцисс среди точек области контакта полосы и выбранного валка при конечно-элементном компьютерном проектировании. Радиус создаваемой дуги соответствует радиусу выбранного валка при конечно-элементном компьютерном моделировании. С помощью инструментария среды автоматизированного компьютерного проектирования определяют длину построенной дуги и полученное значение принимают равным длине дуги контакта полосы и выбранного валка.
Технический результат достигается на примере определения длины дуги контакта верхнего валка и полосы при компьютерном моделировании асимметричной холодной прокатки полосы из стали 08пс с помощью вычислительной среды конечно-элементного анализа DEFORM. Провели испытания на растяжение образцов из стали 08пс на испытательной машине Gleeble-3800 при температуре 20°С, и при скоростях деформации 1 с-1 и 100 с-1.
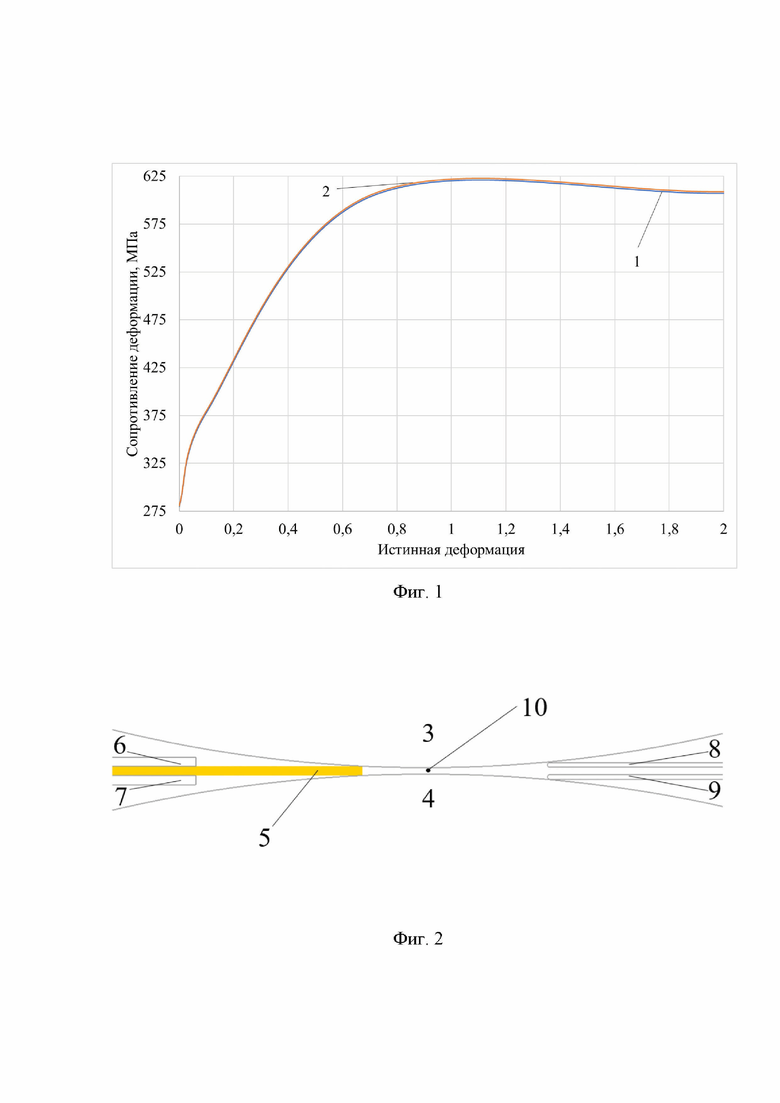
На фиг. 1 представлены результаты испытаний на растяжение: поз.1 - скорость деформации 1 с-1, поз. 2 - скорость деформации 100 с-1. Определенные значения параметров исследуемого процесса прокатки и результаты стандартных испытаний на растяжение образцов из стали 08пс на испытательной машине использовали для проведения компьютерного моделирования исследуемого процесса продольной прокатки в условиях плоского деформированного состояния. Материал полосы - сталь 08пс. Температура заготовки 20°С. Диаметр верхнего валка - 570 мм, диаметр нижнего валка - 600 мм. Для обеспечения скорости прокатки 4200 мм/с вращение верхнего валка происходило со скоростью 14,7368 рад/с, нижнего - 14 рад/с. Моделирование осуществляли в условиях плоского деформированного состояния. Перед прокаткой толщина полосы составляла 2 мм, зазор между валками - 1,4 мм.
Предварительно в среде автоматизированного компьютерного проектирования SolidWorks создали плоский эскиз, содержащий валки, заготовку, толкатель и направляющие. Эскиз сохранили в формате dxf и загрузили в препроцессор DEFORM.
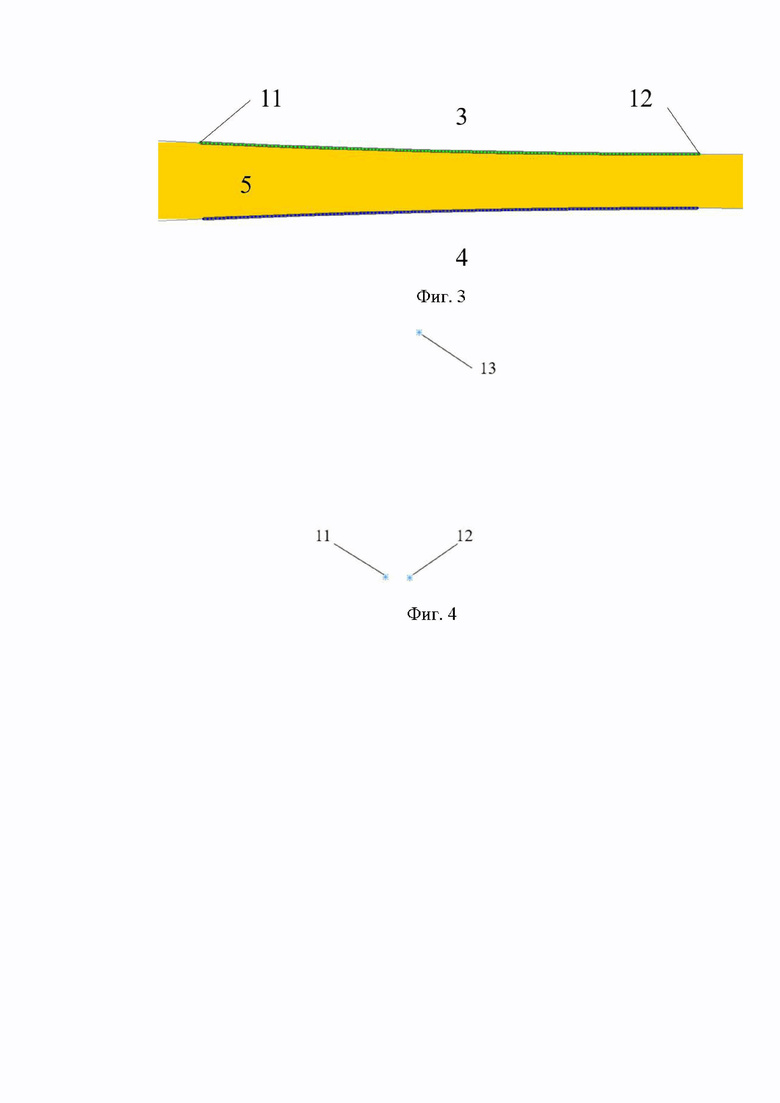
На фиг. 2 показана модель в препроцессоре DEFORM: 3 - верхний валок, 4 - нижний валок, 5 - полоса, 6,7 - направляющие с входной стороны, 8,9 - направляющие с выходной стороны. Для удобства обработки результатов компьютерного проектирования ввели систему координат. При этом начало координат (поз. 10 на фиг. 2) находилось на пересечении вертикальной прямой, проходящей через центр верхнего валка и горизонтальной прямой, проходящей через середину полосы по толщине и параллельной верхнему и нижнему краю полосы. При задании начальных и граничных условий приняли, что валки, толкатель и направляющие являются абсолютно жесткими телами, т.е. не деформируются ни упруго, ни пластически. При задании значений сопротивления деформации ввели в препроцессоре DEFORM результаты стандартных испытаний на растяжение. По окончании моделирования с помощью инструментария DEFORM отобразили области контакта полосы и валков на установившейся стадии прокатки (фиг. 3): 3 - верхний валок, 4 - нижний валок, 5 - полоса, 11 - крайняя левая точка области контакта полосы и верхнего валка, имеющая наименьшую координату по оси абсцисс среди точек области контакта полосы и верхнего валка, 12 - точка области контакта полосы и верхнего валка, имеющая наибольшую координату по оси абсцисс среди точек контакта полосы и верхнего валка.
С помощью инструментария DEFORM определили координаты точки, имеющей наименьшую координату по оси абсцисс среди точек дуги контакта полосы с верхним валком: (-13,02; 1). Также определили координаты точки, имеющей наибольшую координату по оси абсцисс среди точек дуги контакта полосы с верхним валком: (0; 0,7). В среде автоматизированного компьютерного проектирования SolidWorks создали плоский эскиз, в котором с учетом введенной ранее системы координат создали три точки: точку, соответствующую центру верхнего валка (позиция 13 на фиг. 4), точку, соответствующую точке области контакта полосы и верхнего валка имеющей наименьшую координату по оси абсцисс среди точек дуги контакта полосы и верхнего валка (позиция 11 на фиг. 4), точку, соответствующую точке, имеющей наибольшую координату по оси абсцисс среди точек дуги контакта полосы и верхнего валка (поз. 12 на фиг. 4).
С помощью инструментария SolidWorks (команда «Центр дуги» во вкладке «Эскиз») построили дугу, используя созданные в эскизе три точки. При этом центром дуги являлась точка, соответствующая центру верхнего валка (поз. 13 на фиг. 5), а краями дуги являлись точки, соответствующие точке области контакта полосы и верхнего валка, имеющей наименьшую координату по оси абсцисс среди точек дуги контакта полосы и верхнего валка, и точке, имеющей наибольшую координату по оси абсцисс среди точек дуги контакта полосы и верхнего валка (поз. 11 и поз. 12, соответственно, на фиг. 5). С помощью инструментария SolidWorks (команда «Измерить» во вкладке «Анализировать») измерили длину построенной дуги и получили значение, равное 13,02 мм. Это значение приняли равным длине дуги контакта полосы и верхнего валка в исследуемом процессе продольной прокатки.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПРОДОЛЬНОЙ ПРОКАТКИ ПОЛОСЫ НА ГЛАДКОЙ БОЧКЕ | 2023 |
|
RU2814505C1 |
| Способ определения положения нейтрального сечения при продольной прокатке на гладкой бочке | 2023 |
|
RU2826294C1 |
| Способ винтовой прокатки цилиндрической заготовки | 2024 |
|
RU2830507C1 |
| Способ определения площади контакта валка и заготовки при прокатке на гладкой бочке | 2021 |
|
RU2787921C1 |
| Способ оценки длины волокна заготовки при плоском деформированном состоянии | 2022 |
|
RU2794566C1 |
| Способ прогнозирования разрушения заготовок в процессе обработки металлов давлением | 2020 |
|
RU2748138C1 |
| Способ определения профиля валка двухвалкового стана продольной прокатки полосы | 2024 |
|
RU2835278C1 |
| СПОСОБ КОМПЬЮТЕРНОГО ПРОЕКТИРОВАНИЯ ТЕХНОЛОГИЧЕСКОГО ЦИКЛА ПРОИЗВОДСТВА МЕТАЛЛОПРОДУКЦИИ | 2013 |
|
RU2552167C2 |
| Способ определения диаметра отверстия полой оправки на её переднем торце при винтовой прошивке в трёхвалковом стане | 2022 |
|
RU2787931C1 |
| Способ определения площади контакта оправки и заготовки при винтовой прошивке | 2019 |
|
RU2714225C1 |

Изобретение относится к способу определения длины дуги контакта при продольной прокатке полосы на гладкой бочке. Осуществляют определение параметров исследуемого процесса продольной прокатки и компьютерное моделирование исследуемого процесса прокатки в двумерной постановке с использованием значений ранее определённых параметров исследуемого процесса продольной прокатки. Компьютерное моделирование исследуемого процесса прокатки осуществляют путем конечно-элементного компьютерного моделирования исследуемого процесса продольной прокатки с помощью инструментария вычислительной среды конечно-элементного анализа. По завершении конечно-элементного компьютерного моделирования исследуемого процесса продольной прокатки отображают область контакта полосы с выбранным валком, определяют координаты по оси абсцисс точек, находящихся в области контакта и имеющих наибольшую и наименьшую координату по оси абсцисс среди всех точек области контакта полосы и выбранного валка, определяют координаты центра выбранного валка. В среде автоматизированного компьютерного проектирования создают плоский чертёж, в котором создают точки с координатами, соответствующими координатам упомянутых точек с наибольшей и наименьшей координатами по оси абсцисс среди точек контакта полосы и выбранного валка, и создают точку, являющуюся центром выбранного валка. В созданном чертеже с помощью инструментария среды автоматизированного компьютерного проектирования строят дугу через указанные три точки. В результате повышается точность расчета энергосиловых параметров процесса прокатки. 5 ил.
Способ определения длины дуги контакта при продольной прокатке полосы на гладкой бочке, включающий определение параметров исследуемого процесса продольной прокатки в виде диаметра валков, зазора между валками, скорости вращения валков, температуры и размеров полосы перед прокаткой, определение сопротивления деформации материала заготовки недеформированной полосы с помощью стандартных испытаний на растяжение на испытательной машине и компьютерное моделирование исследуемого процесса прокатки в двумерной постановке с использованием значений ранее определённых параметров исследуемого процесса продольной прокатки и результатов стандартных испытаний на растяжение, отличающийся тем, что компьютерное моделирование исследуемого процесса прокатки осуществляют путем конечно-элементного компьютерного моделирования исследуемого процесса продольной прокатки с помощью инструментария вычислительной среды конечно-элементного анализа, причем при подготовке данных для упомянутого компьютерного моделирования вводят систему координат, за начало координат принимают точку, являющуюся пересечением вертикальной прямой, проходящей через центр верхнего валка, и горизонтальной прямой, проходящей через середину полосы по толщине и параллельной верхнему и нижнему краю полосы, при этом ось ординат системы координат направлена вертикально вверх, а ось абсцисс - сонаправлена с направлением прокатки, причем по завершении конечно-элементного компьютерного моделирования исследуемого процесса продольной прокатки с помощью инструментария вычислительной среды конечно-элементного анализа на установившейся стадии прокатки отображают область контакта полосы с выбранным валком, определяют координаты по оси абсцисс точек, находящихся в области контакта и имеющих наибольшую и наименьшую координату по оси абсцисс среди всех точек области контакта полосы и выбранного валка, определяют координаты центра выбранного валка, в среде автоматизированного компьютерного проектирования создают плоский чертёж, в котором создают точки с координатами, соответствующими координатам упомянутых точек с наибольшей и наименьшей координатами по оси абсцисс среди точек контакта полосы и выбранного валка, и создают точку, являющуюся центром выбранного валка, в созданном чертеже с помощью инструментария среды автоматизированного компьютерного проектирования строят дугу через три точки - точку, являющуюся центром выбранного валка, которую принимают за центр дуги, и две точки, соответствующие точкам с наибольшей и наименьшей координатами по оси абсцисс среди точек области контакта полосы и выбранного валка, причем радиус создаваемой дуги соответствует радиусу выбранного валка при конечно-элементном компьютерном моделировании исследуемого процесса продольной прокатки, определяют длину построенной дуги с помощью инструментария среды автоматизированного компьютерного проектирования и полученное значение принимают равным длине дуги контакта для исследуемого процесса продольной прокатки полосы на гладкой бочке.
| Способ определения параметров очага деформации при прокатке | 1984 |
|
SU1319964A1 |
| Способ определения длины дуги контакта при прокатке | 1985 |
|
SU1319945A1 |
| WO 2007068359 A1, 21.06.2007 | |||
| WO 2014156673 A1, 02.10.2014. | |||
Авторы
Даты
2024-04-26—Публикация
2023-06-30—Подача