I
Изобретение относится к вычислительной технике, а именно к аналого Вым вычислительным устройствам, применяемым для моделирования дискретных систем, и может быть использовано при исследовании динамических процессов в дискретных системах управления ШСУ) с амплитудно-импульсной модуляцией, в которых осуществляется формоимпульсное преобразование. . Цель изобретения - повышение точности моделирования динамических процессов в ДСУ путем моделирования сигнала помехи от квантования по времени.
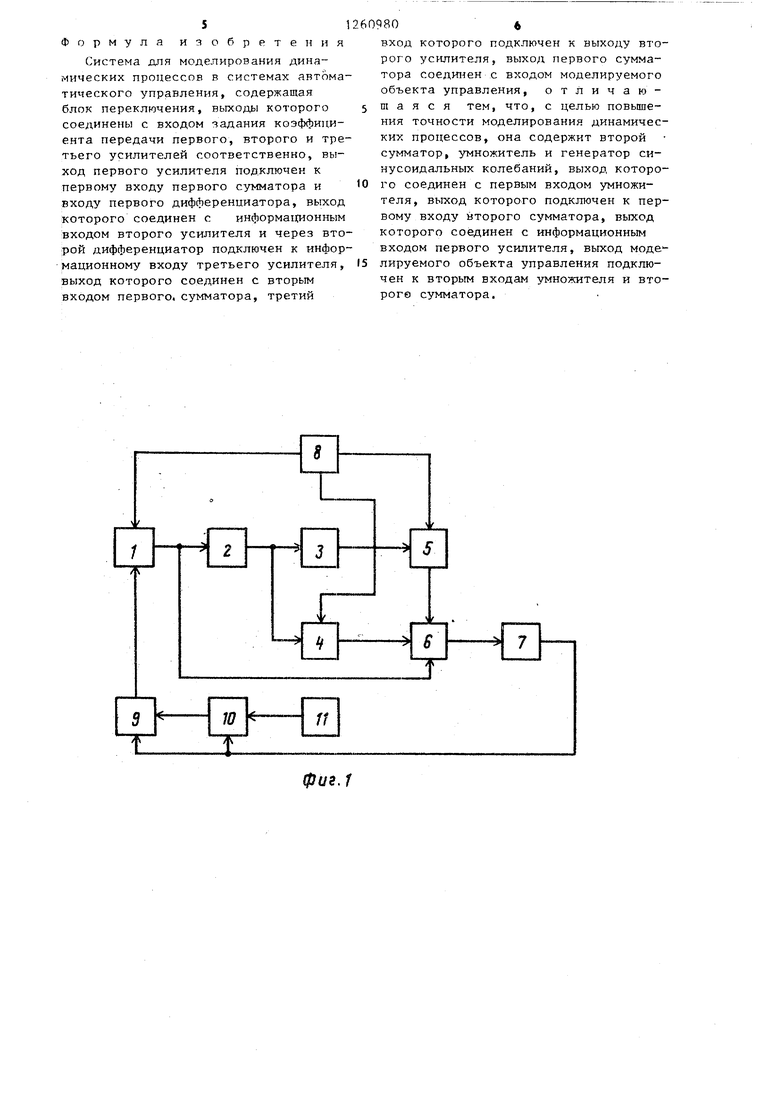
На фиг, 1 представлена структурная схема системы для моделирования динамических процессов в системах автоматического управления; на фиг, 2 и 3 - результаты анализа динамических процессов в дискретной системе автоматического управления,
Система содержит первый усилитель I, первый 2 и второй 3 дифференциаторы, второй Д и третий 5 усилители, первый сумматор 6, моделируемый объект 7 упра вления, блок 8 переключения, второй сумматор 9, умножитель 10 и генератор 11 синусоидальных колебаний,
В основу разработки системы положено использование приближенного эквивалентного представления ДСУ с фор- Моимпульсной коррекцией в виде не- п;peJpывнoй модели.
Известно, что если на вход импульсного элемента ;подается гармонический сигнал x(t)a .со5Ок( t) , сигнал на йыходе формирующего элемента описьта- ется выражением:
12609802
ния приводит к существенному иск-аже- 4, нию входного сигнала.
Ряд в правой части выражений (1) можно аппроксимировать его первым 5 членом () , а все остальные члены ряда считать помехой, вызванной квантованием сигнала по времени в импульсном элементе. При учете лишь первого члена и осуществляется моде- 10 лирование исследуемой системы только по полезному сигналу.
Выражение сигнала помехи можно записать в следующем виде:
15
а Л slDltif i bL Lx ri frr ЧЬ, (« Тпсо ДТо /п
Г Г i-1 --20 (Ч4nQ„) °JJ («,(VnOo)To/n .
(Wj+ncojj -coslTO(2)
,
(с
).
TO
X (
25
30
Раскладывая тригонометрические функции, стоящие в фигурных скобках выражения (2), в ряд Маклорена и ограничиваясь двумя членами ряда, получают выражение для помехи в следующем виде:
2а °° Г
f-r - ZIo iZ (Cosco,t cosna)ot- Ut п
35
- Ь
121:1), d
2n
(3)
40
т- ( cosnG3j,t) +
,Ь. 3i(-1) + .- (coso,t« xcosncOot)l ..
Si X
- ho-oi
1r1
Iu,4 падоУТ- /2n
xcos(co,+nQj(t- .Tj , (1)
где (,)д 2 и/Тд - частота квантования
по времени;
п - количество переключений многократного импульса внутри периода дискретности; oi, - амплитуда импульса
1-го такта внутри периода дискретности. Из выражения (l) следует, что процесс квантования по -времени и последующего формирования требуемых импульсов в дискретной системе управле
а Л slDltif i bL Lx ri frr ЧЬ, (« Тпсо ДТо /п
Г Г i-1 -- (Ч4nQ„) °JJ («,(VnOo)To/n .
(Wj+ncojj -coslTO(2)
,
(с
).
TO
X (
Раскладывая тригонометрические функции, стоящие в фигурных скобках выражения (2), в ряд Маклорена и ограничиваясь двумя членами ряда, получают выражение для помехи в следующем виде:
2а °° Г
f-r - ZIo iZ (Cosco,t cosna)ot- Ut п
- Ь
121:1), d
2n
(3)
т- ( cosnG3j,t) +
,Ь. 3i(-1) + .- (coso,t« xcosncOot)l ..
Поскольку это выражение для сигнала помехи соответствует случаю,
когда на вход импульсного элемента поступает сигнал x(t)a cosco t, то при произвольном входном сигнале можно записать:
i:«.fx(t).cosneo,t-bi|l:n
1 1 n i U
11
-j x(t).cosnu t|
(М,
/
в основу разработки структуры . предлагаемого технического решения положено выражение (4). Анализ выражения (4j показывает, что для моделирования сигнала помехи необходимо сформировать сигнал x(t) COsnu)gt и подвергнуть его тому же преобразованию, что и полезньгй сигнал, причем, как показали исследования, достаточно учитывать в сигнале помехи первую гармонику () .
Коэффициент усиления усилителя 1
1 п
,
усилителя 4
(2i-i)J/2nz:o ;
L Ui - 1-1 еля 5
к,.т; .
усилителя 5
Система содержит генератор 11 синусоидальных колебаний с частотой (i /T и единичной амплитудой.
В системе с блока 8 переключения в зависимости от требуемых значений п и моделируемого процесса фор- моимпульсного преобразования устанавливают соответствующие значения коэффициентов К,, К и К, в усилителях 1, 4 и 5. При включении системы сигнал с-выхода моделируемого объекта 7 управления поступает на первый вход умножителя 10 и на первый вход второго сумматора 9, На второй вход умножителя 10 поступает сигнал cos COgt, С выхода умножителя сигнал помехи x(t)-coscOot поступает на второй вход сумматора 9, Сигнал с выхода сумматора 9 усиливается и по трем цепям подается на входы первого сум- матора 6: по первой цепи - непосредственно, по второй - через дифференциатор 2 и усилитель 4, по третьей - через дифференциаторы 2 и 3 и третий усилитель 5, С выхода первого сумма- тора 6 сигнал, эквивалентный резуль- тату формоимпульсногг преобразования подается на вход моделируемого объекта 7 управления. При исследовании процессов формоимпульсного преоб- разования с другими параметрайи рсу- . ществляется перестройка коэффициентов К,, К и К в усилителях 1, 4 и 5,а также частоты а в генераторе П
На фиг, 2 и 3 приведены результат анализ а динамических процессов в дискретной системе автоматического управления, при этом в системе используется форм 1рователь импульсов при , а объект регулирования представляет собой колебательное звено 2-го порядка с передаточной функцией
5
0
5
0
5 о 0 5 -
WK(P)
К
T pUzfTp+l
где ,8, ,2 с, 0,6. .
Параметры регулятора Т 0,1 с; (i,20,«:,, -10.
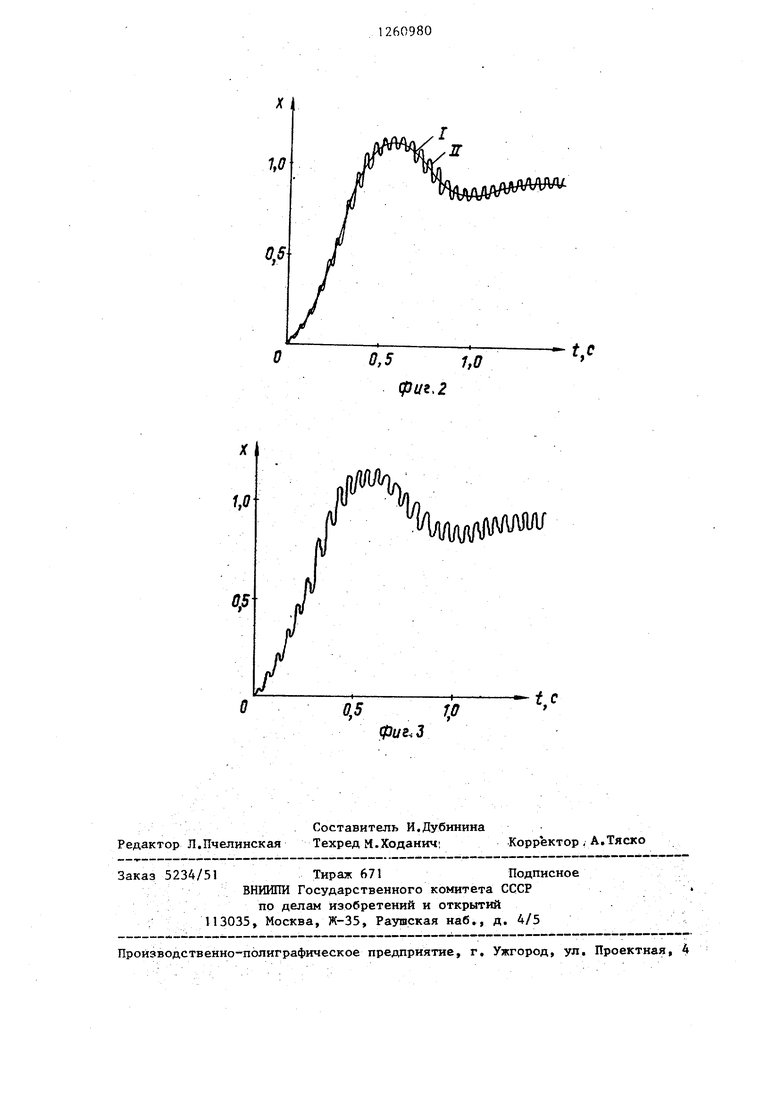
На фиг. 2 представлен процесс изменения выходного сигнала объекта регулирования x(t) при возмущающем воздействии f{t) в виде единичной скачкообразной функции f(t)l(t) при нулевых начальных условиях.
Кривая 1 соответствует моделированию переходного процесса в рассматриваемой дискретной системе автоматического управления при использовании известного устройства, т.е. без учета моделирования помехи от квантования. Кривая II получена при моделировании переходного процесса предлагаемым устройством с учетом 1-й гармоники сигнала помехи от квантования.
Анализ представленных на фиг. 2 зависимостей показывает, что точность моделирования процесса в ДСУ за счс/ моделирования сигнала помехи от квантования значительно повышается.
На фиг. 3 показаны результаты моделирования динамического процесса в ДСУ при учете 1-й и 2-й гармоник сигнала помехи от квантования. Сравнительный анализ динамических процессов при учете одной и двух гармоник сигнала помехи от квантования показывает, что влияние более высоких гармоник в большинстве практических случаев является незначительным. Это объясняется тем, что в большинстве случаев частота квантования по времени О выбирается из условия QQ/4 i(o( где Qд - частота, характеризуемая шириной полосы пропускания непрерьш- ной части системы и определяемая из условия
Kuo)/6--.
S2.
при И Оц .
В этом случае ошибка в точности моделирования динамических процессбв в ДСУ, как показьтают расчеты, не превышает 10% при учете только 1-й гармоники сигнала помехи от квантования.
51
Формула изобретения
Система для моделирования динамических процессов в системах автоматического управления, содержащая блок переключения, выходы которого соединены с входом задания коэффициента передачи первого, второго и третьего усилителей соответственно, выход первого усилителя подключен к первому входу первого сумматора и входу первого дифференциатора, выход которого соединен с информационным входом второго усилителя и через второй дифференциатор подключен к информационному входу третьего усилителя, выход которого соединен с вторым входом первого, сумматора, третий
фиг. Г
80«
вход которого подключен к выходу второго усилителя, выход первого сумматора соединен с входом моделируемого объекта управления, отличаю- m а я с я тем, что, с целью повьппе- ния точности моделирования динамических процессов, она содержит второй сумматор, умножитель и генератор синусоидальных колебаний, выход которого соединен с первым входом умножителя, выход которого подключен к первому входу второго сумматора, выход которого соединен с информационным входом первого усилителя, выход моделируемого обьекта управления подключен к вторым входам умножителя и второго сумматора.

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для моделирования динамических процессов в системах автоматического управления | 1979 |
|
SU866566A1 |
| Устройство для аналогового моделирования динамических процессов в дискретных системах автоматического управления | 1987 |
|
SU1474695A1 |
| Система для моделирования динамических процессов в системах автоматического управления | 1977 |
|
SU645126A1 |
| Бинарная система управления | 1983 |
|
SU1120284A1 |
| Бинарная система управления вынужденным движением | 1983 |
|
SU1117587A1 |
| Бинарная система управления | 1988 |
|
SU1837254A1 |
| Бинарная система управления объектами с запаздыванием | 1986 |
|
SU1383294A1 |
| Дискретная система оценивания | 1989 |
|
SU1727110A1 |
| ДИСКРЕТНАЯ СИСТЕМА ОЦЕНИВАНИЯ | 2007 |
|
RU2398258C2 |
| Способ моделирования эволюции квантовой системы и устройство для его осуществления | 1989 |
|
SU1776354A3 |
Система для моделирования дииа- мических процессов в системах автоматического управления откосится к вычислительной технике, а именно к аналоговым вычислительным устройствам, применяемым для моделирования дискретных систем. Целью изобретения является повышение точности моделирования динамических процессов в дискретных системах управления. Указанная цель достигается тем, что в известную систему дополнительно введены генератор синусоидальных колебаний, блок умножения и сумматор. Введение указанных блоков обеспечи- ,вает моделирование сигнала помехи от квантования по времени. 3 ил.
(
| Устройство для моделирования нелинейных колебательных систем | 1975 |
|
SU516056A1 |
| Г, 05 В 17/02, 1976 | |||
| Система для моделирования динамических процессов в системах автоматического управления | 1977 |
|
SU645126A1 |
| Кипятильник для воды | 1921 |
|
SU5A1 |
Авторы
Даты
1986-09-30—Публикация
1985-03-26—Подача