In 1.IH .
i.n-г l.a-3- 13.
гг- ti
-12
-3.3
-3.
-З.п-2
-З-п-1 In.
(Л
С

| название | год | авторы | номер документа |
|---|---|---|---|
| Последовательный сумматор | 1988 |
|
SU1571573A1 |
| "Преобразователь кода Фибоначчи в код "золотой" пропорции" | 1990 |
|
SU1783616A1 |
| Устройство для умножения | 1987 |
|
SU1444751A1 |
| Преобразователь кодов | 1988 |
|
SU1552380A1 |
| "Преобразователь кода Фибоначчи-1 в код "золотой"-1 пропорции" | 1988 |
|
SU1649671A1 |
| Аналого-цифровой преобразователь | 1981 |
|
SU1005300A1 |
| Устройство для умножения | 1984 |
|
SU1254469A1 |
| Арифметико-логическое устройство двухадресной ЦВМ | 1980 |
|
SU890390A1 |
| Преобразователь р-кода фибоначчи в двоичный код | 1976 |
|
SU662932A1 |
| Устройство для суммирования двоичных чисел | 1988 |
|
SU1578709A2 |
Изобретение относится к вычислительной технике и может быть использовано дпя построения специализированных вычислительных устройств. Цель изобретения расширение области применения за счет преобразования кода золотой пропорции в код Фибоначчи. Преобразователь кодов, имеющий входы разрядов первого информационного входа 1.входы разрядов второго информационного пхода 2, выходы разрядов выхода 3, вход 4 задания режим, содержит коммутатор 5 и сумматор 6 кодов Фибоначчи. 1 ил., 1 табл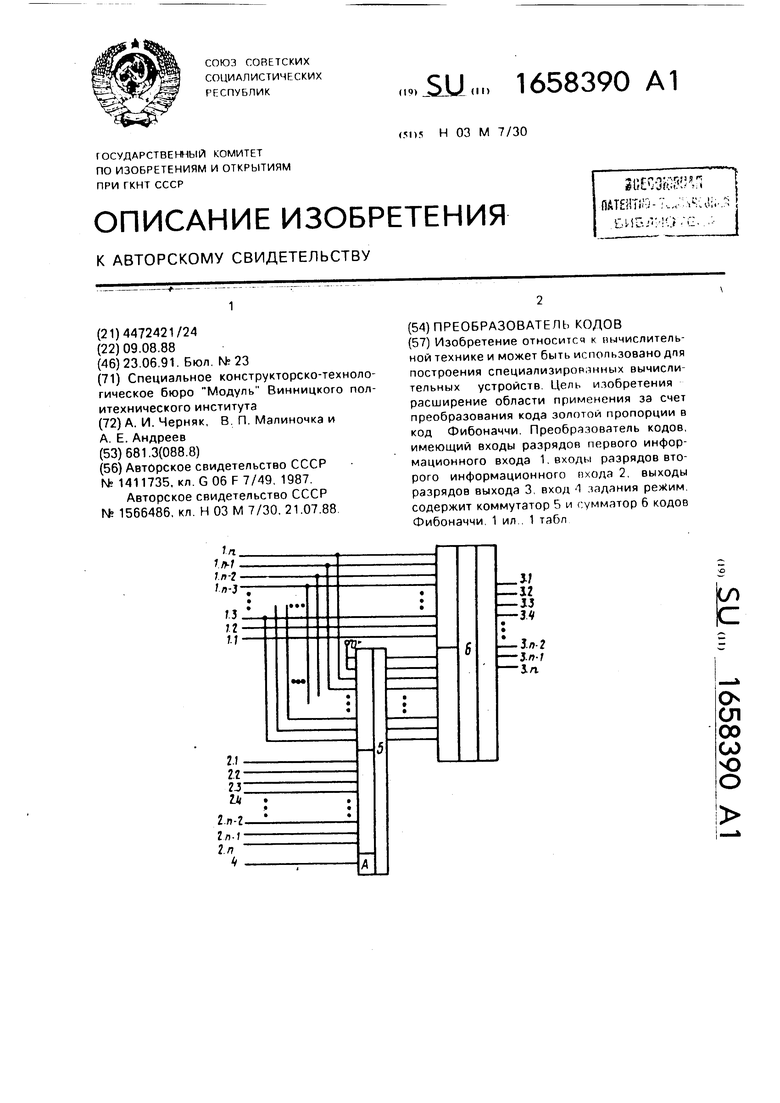
ll 2.Z- 2Jгм
г.п-г.
Z/.J1л
Ь .
о ел
00 GJ О О
Изобретение относится к вычислительной технике и может быть использовано в арифметических устройствах ЭВМ.
Целью изобретения является расширение области применения за счет преобразования кода золотой пропорции в код Фибоначчи.
На чертеже представлена схема преобразователя кодов.
Преобразователь содержит входы 1.1-1.п разрядов первого информационного входа преобразователя, входы 2.1-2.П разрядов второго информационного входа преобразователя, выходы 3.1-З.п разрядов выхода преобразователя, вход 4 задания режима преобразователя, коммутатор 5 и сумматор 6 кодов Фибоначчи.
Сумматор 6 кодов Фибоначчи может быть реализован известным способом.
Сущность и физическая возможность преобразования параллельного кода золотой пропорции в параллельный код Фибоначчи заключается в следующем.
Ряд 1 - чисел Фибоначчи образуется согласно выражения:
ф (п)
0при п О
1при п О
(D
(f (n-1) + р (п-2) при )
и имеет вид 1,1,2,3,5,8,13,21,...
Известно, что существует ряд чисел Люка, в котором каждое число также равно сумме двух предыдущих, однако начальные условия ряда есть 2 и 1.
Ряд чисел Люка образуется согласно
выражения:
0при Цп) 2 при п 0;
1при п 1;
.Цп-1) + Цп-2)при п 0 (2) и имеет вид 2,1,3,4,7,11,18,29,49...
Известна также связь степеней золотой пропорции с числами Люка для положительных п, которая выражается в следующем:
L (п)
для четных п - о + а (дпя нечетных п - о - а п(3)
где а - основание системы счисления золотой пропорции:
а -4р 1,618.... п - номер разряда кода.
Произведем вычитание чисел Фибоначчи р (п) из чисел Люка Цп). Результат представлен в таблице.
Из таблицы видно,что начиная с
результат вычитания является рядом чисел Фибоначчи pi (п).
Таким образом, при преобразовании кода золотой пропорции в 1 - код Фибоначчи необходимо сложить два кода, первый
код является кодом Фибоначчи, содержащим единицы в тех же разрядах, что и исходный код золотой пропорции, второй код является тем же кодом, сдвинутым на два разряда в сторону младших разрядов.
При этом учитывая, что разряды счетными номерами кода расположены через один разряд друг от друга, и также разряды с нечетными номерами расположены через один разряд друг от друга, общие суммы а п
для четных п, а также для нечетных п не превышают единицы. Это следует из того свойства кодов золотой пропорции, что при минимальной форме кода вес старшего разряда больше любого кода, записанного в
младших разрядах. Учитывая то, что в коде золотой пропорции могут встречаться единицы, как в четных так и нечетных номерах разрядов, общая погрешность преобразования кода золотой пропорции с положительными значениями п будет равна разности суммы для нечетных номеров разрядов и суммы а п для четных номеров разрядов.
Для преобразования параллельного кода золотой пропорции в параллельный код Фибоначчи необходимо сложить параллельный код золотой пропорции с этим же кодом, сдвинутым на два разряда в сторону младших разрядов по правилам сложения
кодов Фибоначчи, а сумма единиц с весом разрядов а п будет меньше единицы и в преобразовании может не участвовать (не учитываться).
Рассмотрим работу преобразователя
кодов. При выполнении операции сложения на вход 4 подается единичный сигнал, который управляет работой коммутатора 5 и подключает входы 2.1 ...2.п к входам сумматора 6, который производит аналогичные аналогу сложения кодов Фибоначчи
При выполнении операции преобразования параллельного кода золотой пропор- циии в параллельный код Фибоначчи на вход 4 поступает нулевой сигнал, который управляет коммутатором 5 и входы 1.3 ..1.п подключает к входам сумматора 6, который производит сложение и формирует на выходах 3.1-3.п результат преобразования.
Формула изобретения Преобразователь кодов, содержащий коммутатор и сумматор кодов Фибоначчи, причем входы разрядов первого информационного входа преобразователя соединены с входами соответствующих разрядов входа первого слагаемого сумматора кодов Фибоначчи, выходы разрядов суммы которого являются выходами соответствующих разрядов выхода преобразователя, входы разрядов второго информационного входа которого соединены с входами соответствующих разрядов первого информационного входа коммутатора, выходы разрядов выхода которого соединены с входами соответ
5
ствующих разрядов вуода второго слагаемого сумматора кодов Фибоначчи, отличающийся тем, что, с целью расширения области применения за счет преобразования кода золотой пропорции в код Фибоначчи, вход задания режима преобразователя соединен с управляющим входом коммутатора, входы двух старших разрядов второго информационного входа которого соединены с входом нулевого потенциала преобразователя, входы разрядов первого информационного входа которого соединены со сдвигом на два разряда в сторону младших разрядов с входами разрядов второго информационного входа коммутатора.
| Сумматор кодов Фибоначчи | 1987 |
|
SU1411735A1 |
| Преобразователь кодов с иррациональным положительным основанием в коды с иррациональным отрицательным основанием | 1988 |
|
SU1566486A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Выбрасывающий ячеистый аппарат для рядовых сеялок | 1922 |
|
SU21A1 |
Авторы
Даты
1991-06-23—Публикация
1988-08-09—Подача