Изобретение относится к области вычислительной техники, в частности к устройствам сложения чисел с плавающей запятой, и может быть использовано при разработке арифметических устройств микропроцессоров как универсальных, так и специализированных.
В операции сложения чисел с плавающей запятой предварительный порядок результата равен порядку большего по абсолютной величине операнда ПВ. Если результат требует нормализации, то предварительный порядок результата уменьшается на величину, называемую порядком коррекции, равную количеству старших незначащих цифр мантиссы SH. Согласно стандарту «ANSI/IEEE 754» на двоичную арифметику, порядок результата должен быть целым числом, не меньшим единицы. Таким образом, результат не должен сдвигаться влево на количество разрядов, превосходящее максимальную допустимую для данных операндов величину М, которая равна М=ПБ-1, то есть порядку большего операнда минус 1. Величина М называется кодом ограничения. Если М меньше количества старших незначащих цифр, то мантисса сдвигается влево на М разрядов, и результат будет денормализованным числом, обеспечивая тем самым режим постепенного отрицательного переполнения.
Согласно стандарту при получении денормализованного результата в случае открытой маски прерывания "underflow" происходит его масштабирование. Оно заключается в том, что мантисса нормализуется без учета кода ограничения. Если порядок результата получается нулевым или отрицательным, то к нему прибавляется масштабирующая константа 3·213. При этом порядок результата становится положительным и вырабатывается прерывание "underflow".
Известно устройство для коррекции порядка результата сложения чисел с плавающей запятой, содержащее сумматор коррекции порядка, на первый и второй входы которого поступают соответственно порядок большего числа и порядок коррекции (Behrooz Parhami, Computer Arithmetic: Algorithm and Hardware Implementation, стр.302, Oxford University Press, 2000).
К недостаткам данного устройства можно отнести отсутствие формирования сигнала масштабирования, что не дает возможности учитывать масштабирующую константы, когда порядок результата получается нулевым или отрицательным, а также не учтено то, что разряды порядка коррекции формируются в разные моменты времени, и это существенно замедляет вычисление порядка результата.
Наиболее близким по технической сущности к изобретению является устройство для коррекции порядка результата сложения чисел с плавающей запятой, являющегося частью системы, содержащей схему определения кода сдвига влево, схему определения сдвига вправо на один разряд, инкрементор, инвертор кода сдвига влево, и сумматор коррекции порядка (US №6301594, кл. G 06 F 7/00, от 2001).
Недостатком данного устройства является отсутствие учета масштабирующей константы, когда порядок результата получается нулевым или отрицательным, а также длительный процесс суммирования, обусловленный тем, что сумматор начинает работу после прихода последнего разряда порядка коррекции.
Техническим результатом является ускорение процесса суммирования при коррекции порядка результата сложения чисел с плавающей запятой, а также обеспечение учета масштабирующей константы при получении денормализованного результата в случае открытой маски прерывания "underflow" ("андерфлоу").
Достигается это тем, что устройство для коррекции порядка результата сложения чисел с плавающей запятой содержит блок формирования сигнала масштабирования, входы разрешения масштабирования результата, кода ограничения и коррекции порядка которого являются соответственно первым, вторым и третьим входами устройства, выход подключен к первому информационному входу сумматора коррекции порядка, второй информационный вход которого является четвертым входом устройства, третий вход которого соединен с третьим информационным входом сумматора коррекции порядка, выход которого является выходом устройства, согласно изобретению содержит сумматор коррекции порядка, который содержит три узла, первый из которых выполняет следующие функции:
Х1=ПБ6А6,
Р6=А6+ПБ6,
Х2=Х1+Р6А5ПБ5,
Р5-6=Р6(А5+ПБ5),
Х3=Х1+Р5-6А4ПБ4,
Р4-6=Р5-6(А4+ПБ4),
Х4=Х3+Р4-6А3ПБ3
Р3-6=Р4-6(А3+ПБ3),
Х5=Х4+Р3-6А2ПБ2,
Р2-6=Р3-6(А2+ПБ2),
Y1=Cin+ПБ1,
Y2=СinПБ1,
G6=X5+Y2P2-6+P2-6A1Y1,
второй узел выполняет следующую функцию:
G13=G6+(ПБ13+ПБ12+...+ПБ8+ПБ7),
и третий узел выполняет следующие функции:

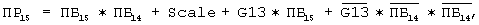
где G6, G13 - сигналы переноса из шести и тринадцати младших разрядов соответственно, Scale - сигнал масштабирования, Сin - сигнал входного переноса. A6, A5, A4, А3, А2, A1 - значения инверсий сигналов SH32l, SH16l, SH8l, SH4l, SH2l, SH1l, кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно, Хi, Yj - промежуточные сигналы, i, j - целые числа, i из интервала от 1 до 5, j из интервала от 1 до 2, Р2-6, Р3-6, Р4-6, Р5-6, Р6 - сигналы распространения переноса соответственно через разряды со 2-го по 6-ой, с 3-го по 6-ой, с 4-го по 6-ой, с 5-го по 6-ой и 6-ой разряд, ПБ15, ПБ14,...,ПБ2, ПБ1 - сигналы порядка большего слагаемого соответственно 15-го, 14-го,..., 1-го разрядов, кроме того, блок формирования сигнала масштабирования выполняет следующую логическую функцию:
Scale=ScaleEN*

где Scale - сигнал масштабирования, SH64l, SH32l, SH16l, SH8l, SH4l, SH2l, SH1l, сигналы кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно, М7, M6,..., M1 - сигналы кода ограничения соответственно 7-го, 6-го,..., 1-го разрядов, ScaleEN - сигнал разрешения масштабирования результата.
Сущность изобретения заключается в том, что выполнение заявляемого устройства вышеописанным образом с использованием сумматора коррекции порядка и блока формирования сигнала масштабирования, позволяет обеспечить высокое быстродействие при значительном упрощении устройства.
Сравнение заявляемого устройства с ближайшим аналогом позволяет утверждать о соответствии критерию "новизна", а отсутствие
в аналогах отличительных признаков заявляемого устройства говорит о соответствии критерию "изобретательский уровень".
Предварительные испытания позволяют судить о возможности широкого промышленного использования.
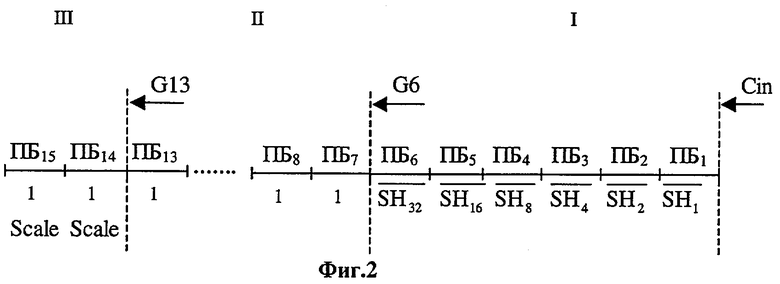
На фиг.1 представлена блок-схема устройства для коррекции порядка результата сложения чисел с плавающей запятой, на фиг.2 представлен принцип структурного разбиения сумматора коррекции порядка на отдельные узлы, на фиг.3 представлен пример реализации первого узла сумматора коррекции порядка по соответствующим логическим формулам.
Устройство содержит блок 1 формирования сигнала масштабирования, сумматор 2 коррекции порядка, первый, второй, третий и четвертый входы 3-1-3-4 и выход 3-5. Выход 4 блока 1 формирования сигнала масштабирования подключен к первому информационному входу 5-1 сумматора 2 коррекции порядка, второй вход 5-2 которого является четвертым входом 3-4 устройства, а третий вход 5-3 подключен к третьему входу 3-3 устройства. Входы 3-1-3-3 являются входами блока 1 формирования сигнала масштабирования, а выход 3-5 устройства является выходом сумматора 2 коррекции порядка.
Блок 1 формирования сигнала масштабирования выполняет следующую логическую функцию:
Scale=Scale EN*
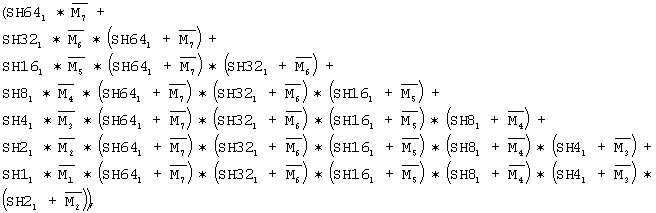
где Scale - сигнал масштабирования, SH64l, SH32l, SH16l, SH8l, SH4l, SH2l, SH1l, сигналы кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно, М7, М6,..., M1 - сигналы кода ограничения соответственно 7-го, 6-го,..., 1-го разрядов, ScaleEN - сигнал разрешения масштабирования результата.
Сумматор 2 коррекции порядка, содержит три узла, первый из которых выполняет следующие функции:
Х1=ПБ6А6,
Р6=А6+ПБ6,
Х2=Х1+Р6А5ПБ5,
Р5-6=Р6(А5+ПБ5),
Х3=Х1+Р5-6А4ПБ4,
Р4-6=Р5-6(А4+ПБ4),
Х4=Х3+Р4-6А3ПБ3,
Р3-6=Р4-6(А3+ПБ3),
Х5=Х4+Р3-6А2ПБ2,
Р2-6=Р3-6(А2+ПБ2),
Y1=Cin+ПБ1,
Y2=СinПБ1,
G6=X5+Y2P2-6+P2-6A1Y1,
второй узел выполняет следующую функцию:
G13=G6+(ПБ13+ПБ12+...+ПБ8+ПБ7),
и третий узел выполняет следующие функции:

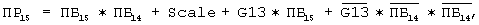
где G6, G13 - сигналы переноса из шести и тринадцати младших разрядов соответственно, Scale - сигнал масштабирования, Сin - сигнал входного переноса, А6, А5, А4, A3, А2, A1 - значения инверсий сигналов SH32l, SH16l, SH8l, SH4l, SH2l, SH1l, кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно, Хi, Yj - промежуточные сигналы, i, j - целые числа, i из интервала от 1 до 5, j из интервала от 1 до 2, Р2-6, Р3-6, P4-6, Р5-6, Р6 - сигналы распространения переноса соответственно через разряды со 2-го по 6-ой, с 3-го по 6-ой, с 4-го по 6-ой, с 5-го по 6-ой и 6-ой разряд, ПБ15, ПБ14,..., ПБ2, ПБ1 - сигналы порядка большего слагаемого соответственно 15-го, 14-го,..., 1-го разрядов.
Пример реализации первого узла сумматора коррекции порядка по соответствующим логическим формулам представлен на фиг.3, где логический блок 6 является элементом типа ИЛИ, а логические блоки блоки 7-11 являются элементами типа 2-1-И-ИЛИ.
Устройство работает следующим образом
Рассмотрим Блок 1 формирования сигнала масштабирования Scale:
Scale=ScaleEN*
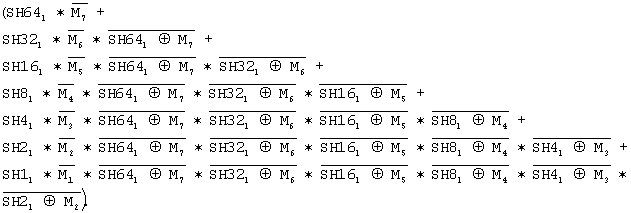
Он стробируется сигналом разрешения масштабирования результата ScaleEN. Далее, Scale равен "1", если SH64l="1", a M7="0" (первое слагаемое в скобках). Если SH64l=М7, то переходим к сравнению сомножителей второго слагаемого. Если SH32l="1", а M6="0", то вырабатывается Scale. Если SH64l=М7 и SH32l=M6, то переходим дальше и анализируем разряды SH16l и M5.
Этот процесс заканчивается сравнением разрядов SH1l и Ml.
Таким образом, сигналы SHl и М поразрядно сравниваются, начиная со старших разрядов; если разряд SHl больше соответствующего разряда М, то вырабатывается сигнал масштабирования, иначе переходим к сравнению более младших разрядов. Используя несколько раз булево тождество 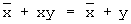 , можно преобразовать выражение для Scale к следующему виду:
, можно преобразовать выражение для Scale к следующему виду:
Scale=ScaleEN*

Выражение для сигнала Scale можно разложить относительно SH1l.
Scale=A1+B1*SH1l,
где A1 и В1 - это функции, зависящие от SH2l, SH4l, SH8l, SH16l и SH32l.
Зависимость от М несущественна с точки зрения задержки, так как М формируется заранее. A1 и B1 можно подготовить за то же время, что и SH1l. Таким образом, это выражение можно получить за один логический уровень на элементе 1И-2И-2ИЛИ.
Аналогичным образом можно разложить A1 и B1 относительно SH2l.
A1=A2a+B2a*SH2l,
В1=А2b+В2b*SH21,
Здесь А2a, В2a, А2b и В2b - это функции, зависящие от SH4l, SH8l, SH16l и SH32l.
Эти выражения можно реализовать за один логический уровень после получения SH2l, А2a, В2a, A2b и В2b. Таким образом, последовательное разложение сигнала Scale по разрядам SHl дает возможность реализовать его через один логический уровень после появления SH1l.
На фиг.2 показано разбиение сумматора 2 коррекции порядка на три соответствующих узла: узел с разрядами с "1" по "6", узел с разрядами с "7" по "13" и узел с двумя старшими разрядами.
"15"-разрядный порядок большего (двойной расширенный формат) поступает в сумматор в прямой фазе, "6"-разрядный код сдвига инвертируется, при этом "9" старших разрядов второго слагаемого заполняются единицами. Кроме того, в два старших разряда сумматора заводится сигнал масштабирования Scale.
Сложение происходит в обратном коде, а так как сумма согласно стандарту должна быть положительной (Еmin="1"), то всегда будет циклический перенос, поэтому в сумматор надо заводить Сin=1.
С другой стороны, когда количество старших незначащих цифр мантиссы равно "64", разряды кода сдвига с SH32l по SH1l равны "1", то есть в сумматоре от порядка большего отнимается код 111111, а надо отнимать код 1000000. Если в этом случае сделать Сin="0", то это будет эквивалентно дополнительному вычитанию "1" из порядка большего. Таким образом, полагаем 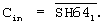
Перенос из "6" младших разрядов G6 можно разложить последовательно по инверсиям разрядов кода сдвига SH1l, SH2l,..., SH32l и получить его через один логический уровень после прихода SH11. Пример реализации на фиг.3.
Переносы в младшие "6" разрядов сумматора можно вычислить не медленнее, чем G6, то есть, "1"-"6" разряды порядка результата можно получить через два логических уровня после SH1l.
Сумма в средней группе определяется сигналом G6:
- если перенос есть, то сумма равна ПБ13, ПБ12,..., ПБ8, ПБ7,
- если переноса нет, сумма равна {ПБ13, ПБ12,..., ПБ8, ПБ7}+{11...11) (ее можно вычислить заранее).
Таким образом, сумму в разрядах с "7" по "13" также можно вычислить через "2" логических уровня после прихода SH1l.
Перенос из "13" разрядов G13 используется для вычисления двух старших разрядов суммы. Очевидно, что
G13=G6+(ПБ13+ПБ12+...+ПБ8+ПБ7).
Выражение можно вычислить за то же время, что и G6, так как оно
отличается только слагаемыми в скобках, которые не зависят от SHl.
Для "14"-ого и "15"-ого разрядов суммы можно написать:

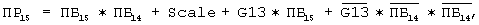
что можно реализовать за один логический уровень после получения G13.
Таким образом, все разряды порядка результата можно сформировать через "2" логических уровня после получения младшего разряда кода сдвига SH1l.
Таким образом, предложенное устройство позволяет ускорить процесс суммирования при коррекции порядка результата сложения чисел с плавающей запятой, а также учесть масштабирующую константу при получении денормализованного результата в случае открытой маски прерывания "underflow" ("андерфлоу").
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ СУММИРОВАНИЯ МАНТИСС И НОРМАЛИЗАЦИИ РЕЗУЛЬТАТА ПРИ ВЫЧИСЛЕНИЯХ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ | 2003 |
|
RU2242045C1 |
| Арифметическое устройство с фиксированной точкой | 1984 |
|
SU1241230A1 |
| Устройство для сдвига информации | 1983 |
|
SU1188783A2 |
| УСТРОЙСТВО ПРИЕМА ИНФОРМАЦИИ ИЗ КАНАЛА | 1998 |
|
RU2137320C1 |
| Устройство обнаружения и коррекции ошибки модулярного кода | 2017 |
|
RU2653257C1 |
| Устройство для сложения (I) | 1989 |
|
SU1837281A1 |
| АКУСТИЧЕСКИЙ ПРЕОБРАЗОВАТЕЛЬ С ПРОСТРАНСТВЕННОЙ ИЗБИРАТЕЛЬНОСТЬЮ ПО ДАЛЬНОСТИ | 1992 |
|
RU2026609C1 |
| Сумматор порядков чисел (II) | 1989 |
|
SU1837282A1 |
| Устройство для вычисления симметрических булевых функций | 1991 |
|
SU1835542A1 |
| Специализированный процессор | 1983 |
|
SU1144117A1 |

Изобретение относится к области вычислительной техники. Техническим результатом является ускорение процесса суммирования и обеспечение учета масштабирующей константы. Указанный результат достигается за счет того, что устройство содержит сумматор коррекции порядка, блок формирования сигнала масштабирования, входы разрешения масштабирования результата, кода ограничения и коррекции порядка которого являются соответственно первым, вторым и третьим входами устройства, а выход подключен к первому информационному входу сумматора коррекции порядка, второй информационный вход которого является четвертым входом устройства, третий вход устройства соединен с третьим информационным входом сумматора коррекции порядка, выход которого является выходом устройства. 1 з.п. ф-лы, 3 ил.
Х1=ПБ6А6,
Р6=А6+ПБ6,
Х2=Х1+Р6А5ПБ5,
Р5-6=Р6(А5+ПБ5),
Х3=Х1+Р5-6А4ПБ4,
Р4-6=Р5-6(А4+ПБ4),
Х4=Х3+Р4-6А3ПБ3
Р3-6=Р4-6(А3+ПБ3),
Х5=Х4+Р3-6А2ПБ2,
Р2-6=Р3-6(А2+ПБ2),
Y1=Cin+ПБ1,
Y2=СinПБ1,
G6=X5+Y2P2-6+P2-6A1Y1,
второй узел выполняет следующую функцию:
G13=G6+(ПБ13+ПБ12+...+ПБ8+ПБ7),
и третий узел выполняет следующие функции:
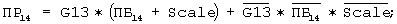

где G6, G13 - сигналы переноса из шести и тринадцати младших разрядов соответственно,
Scale - сигнал масштабирования,
Cin - сигнал входного переноса,
А6, А5, А4, А3, A2, A1 - значения инверсий сигналов SH32l, SH16l, SH8l, SH4l, SH2l, SH1l, кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно,
Xi, Yj - промежуточные сигналы, i, j - целые числа, i из интервала от 1 до 5, j из интервала от 1 до 2,
Р2-6, Р3-6, Р4-6, Р3-6, Р6 - сигналы распространения переноса соответственно через разряды со 2-го по 6-й, с 3-го по 6-й, с 4-го по 6-й, с 5-го по 6-й и 6-й разряд,
ПБ15 ПБ14,...ПБ2, ПБ1 - сигналы порядка большего слагаемого соответственно 15-го, 14-го,..., 1-го разрядов.
Scale=ScaleEN*

где Scale - сигнал масштабирования,
SH64l, SH32l, SH16l, SH8l, SH4l, SH2l SH1l, сигналы кода сдвига с учетом ограничения величины сдвига соответственно на "32", "16", "8", "4", "2", "1" разряд соответственно,
М7, М6,...M1 - сигналы кода ограничения соответственно 7-го, 6-го,...1-го разрядов,
ScaleEN - сигнал разрешения мастабирования результата.
| US 6301594 А, 09.10.2001 | |||
| Устройство для нормализации чисел | 1980 |
|
SU862139A1 |
| Устройство для нормализации и округления чисел с плавающей запятой | 1987 |
|
SU1465879A1 |
| Устройство для выравнивания порядков чисел | 1982 |
|
SU1030798A1 |
| US 6154760 А, 28.11.2000. | |||
Авторы
Даты
2006-01-10—Публикация
2004-04-26—Подача